Дисперсионные и поляризационные свойства азимутально-несимметричных волн круглого открытого слоистого феррит-диэлектрического волновода

Круглый открытый слоистый феррит-диэлек-трический волновод (рис. 1) представляет собой ферритовую трубку с внутренним и внешним радиусами a и b соответственно. Ферритовый слой намагничен до насыщения постоянным магнитным полем H о , направленным вдоль оси z , в положительном направлении которой распространяется электромагнитная волна частоты to. Постановка краевой задачи для рассматриваемой направляющей структуры приведена в [1]. При решении задачи используются метод частичных областей и метод укорочения дифференциального уравнения [2].

Поле электромагнитной волны в круглом открытом продольно намагниченном слоистом феррит-диэлектрическом волноводе является всегда (и при отсутствии у него угловой зависимости) гибридным, поэтому соответствующая краевая задача является [3; 4] несамосопряжен-

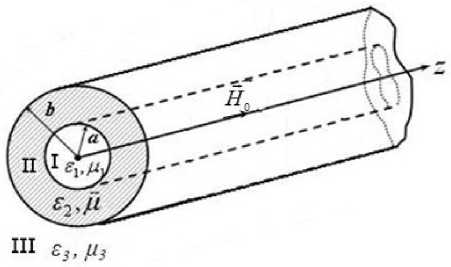
Рис. 1. Круглый открытый слоистый феррит-диэлектриче-ский волновод ной как при отсутствии, так и при наличии потерь в образующих структуру средах. Поскольку [5] собственные значения несамосопряженной краевой задачи в общем случае комплексные, то наиболее общими решениями дисперсионного уравнения волн круглого открытого слоистого феррит-диэлектрического волновода будут комплексные волновые числа Р = Р' + iР".

Так как волны рассматриваемой направляющей структуры принципиально гибридные, будем условно классифицировать их как HE _nm , где первый индекс n означает число вариаций поля по азимутальной координатеф ( n = 0,1, 2, ...), второй индекс m — номер волны ( m = 1, 2, 3, ...).

На рис. 2 и 3 приведены соответственно дисперсионные характеристики нескольких волн с азимутальным индексом n = 1 и n = -1 круглого открытого слоистого феррит-диэлектрического волновода без потерь с параметрами: a = 10 мм; b = 20 мм; Б 1 = S 3 = Е о ; £ 2 = 14,8£ о ; частота ферромагнитного резонанса f = 1,76 ГГц; намагниченность насыщения феррита M s = 103,5 кА/м. Здесь и далее k = ® / ^с , где c — скорость света в вакууме.

Поскольку исследование свойств поверхностных волн волновода без потерь было проведено в [1], в данной работе остановим свое внимание на комплексных волнах [5]. Точки B , C , D на рис. 2 и 3 являются точками жордановой кратности,

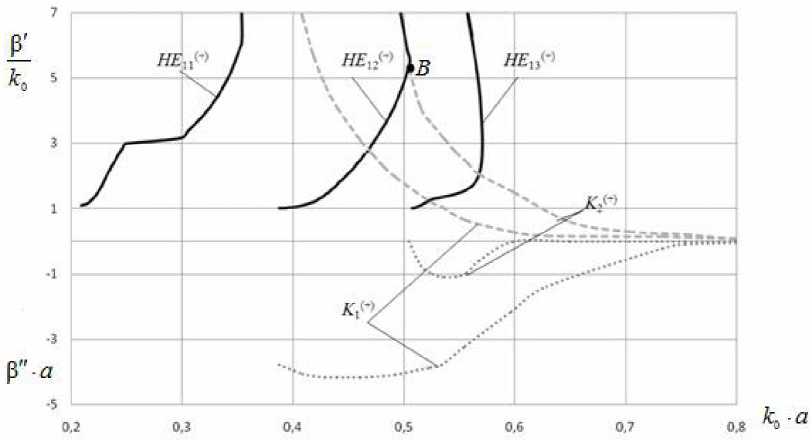
Рис. 2. Дисперсионные характеристики волн с азимутальным индексом n = 1 волновода без потерь

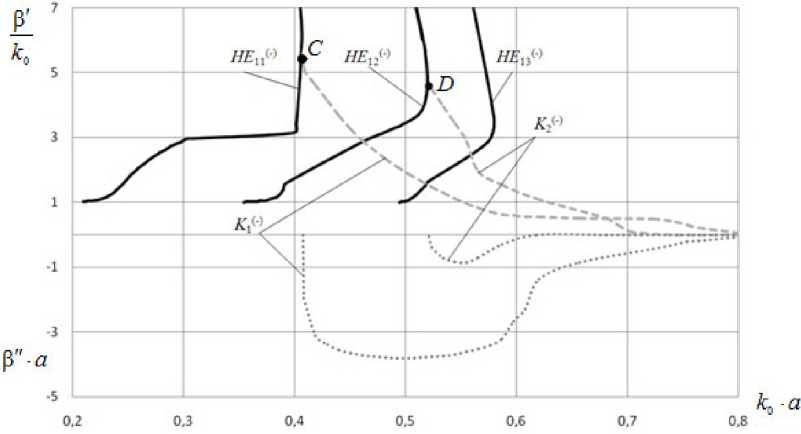
Рис. 3. Дисперсионные характеристики волн с азимутальным индексом n = - 1 волновода без потерь

в которых соединяются участки дисперсионных характеристик с нормальной и аномальной дисперсией волн HE₁₂ , HE₁₁ , HE₁₂ соответственно. В этих точках возникают собственные комплексные волны K 2 + ) , K ( - ) и K - ) • Комплексная волна K 1 ^{+ )} также образуется в точке жордановой кратности при соединении участков дисперсионной характеристики волны HE^ ) с нормальной и аномальной дисперсией, однако эта точка находится за пределами координатного поля. Указанные комплексные волны во всем частотном диапазоне их существования обладают аномальной дисперсией и в среднем за период не переносят энергии вдоль оси направляющей структуры.

Дисперсионные характеристики волн с азимутальными индексами n = 1 и n = -1 круглого открытого слоистого феррит-диэлектрического волновода, полученные при учете магнитных потерь в феррите, представлены на рис. 4 и 5, соответственно.

Параметры направляющей структуры полагались следующими: a = 10 мм; b = 20 мм; s ^ = S 3 = = s₀; s₂ = 14,8s₀; f₀ = 1,76 ГГц; M s = 103,5 кА/м; ширина линии ферромагнитного резонанса A H = = 8 кА/м.

Как видно из рис. 4 и 5, из-за наличия потерь в феррите дисперсионные характеристики волн не терпят разрыва на частоте ферромагнитного резонанса. Волны НКЦ и HE⁽ 2) ведут себя качественно одинаково. В отличие от них, волны ^{( + )          (} )                ⁽ )

HE13 , HE12 и HE13 в области низких частот имеют продолжение в виде быстрых собственных волн. Волна HE1(1) во всем диапазоне частот является медленной.

Из рис. 4 и 5 также следует, что азимутально-несимметричные волны с левой и правой кру-

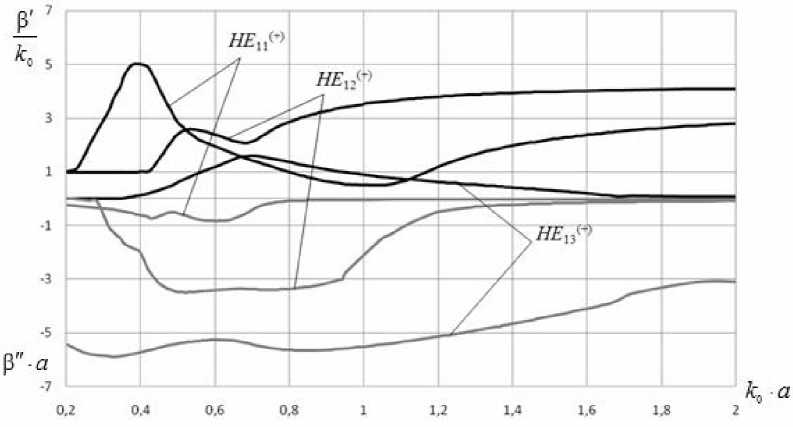
Рис. 4. Дисперсионные характеристики волн с азимутальным индексом n = 1 волновода с потерями

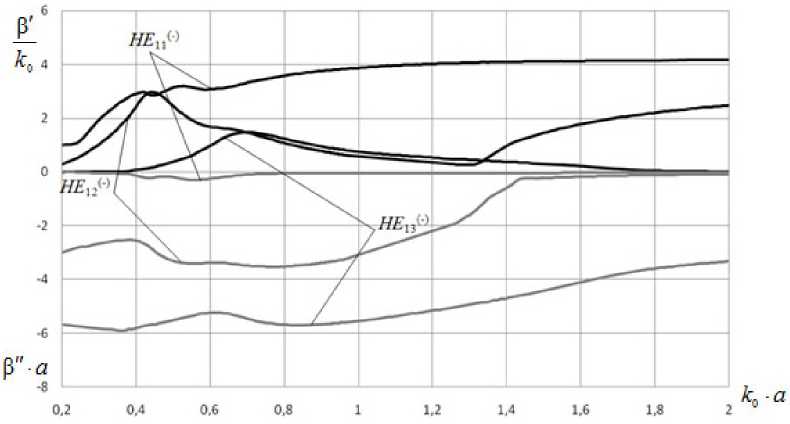
Рис. 5. Дисперсионные характеристики волн с азимутальным индексом n = - 1 волновода с потерями

говой поляризацией HE n^ и HE n^ имеют различные постоянные распространения и коэффициенты затухания, в результате чего при распространении в рассматриваемой структуре изначально линейно поляризованной волны будет происходить изменение ее поляризации – волна станет эллиптически поляризованной. При этом большая полуось эллипса поляризации будет поворачиваться относительно первоначального направления колебаний вектора напряженности электрического поля на угол 9, который при фиксированных параметрах феррита зависит от частоты to и длины волновода L .

Угол поворота большой полуоси эллипса поляризации и его эксцентриситет определяются по формулам [6]:

9=e : -₽l L ,

e =

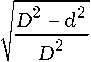
где в' ⁺ и в' — вещественные части продольных волновых чисел волн HE 1 + ) и HE^ ) соот-

ветственно;

d = A

D = A [exp ( '' ^- L ) + exp ( в "⁺ L )

exp ( в'' ^- L ) - exp ( "⁺ L

большая

и

и

малая полуоси эллипса поляризации; А – амплитуда циркулярно поляризованной волны на входе волновода; в'' ⁺ и в'' — мнимые части продольных волновых чисел волн HE^ ) и HE^ ) .

На рис. 6 и 7 для волны HE₁₁ волновода с потерями приведены графики частотных зависимостей погонного угла поворота большой полуоси эллипса поляризации ф = 9 / L и эксцентриситета эллипса e соответственно.

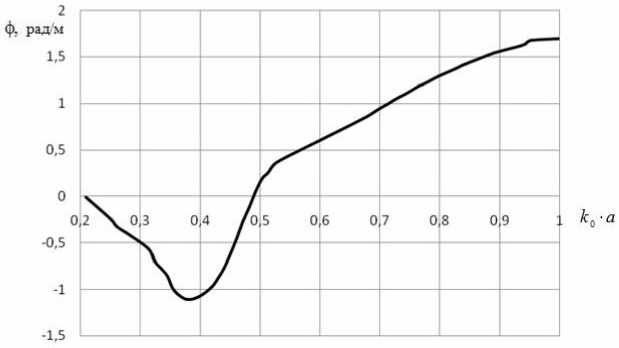
Рис. 6. Частотная зависимость погонного угла поворота большой полуоси эллипса поляризации для волны HE₁₁ волновода с потерями

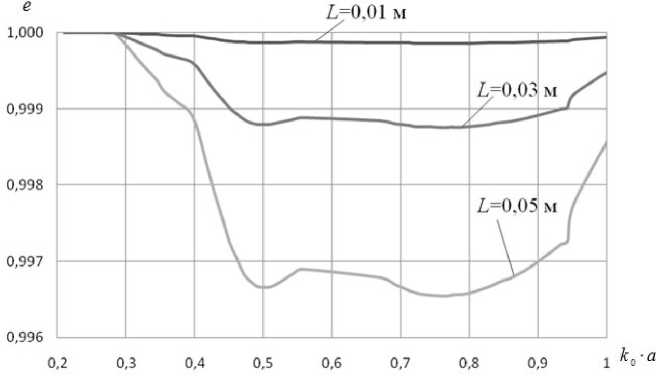
Рис. 7. Частотная зависимость эксцентриситета эллипса поляризации для волны HE₁₁ волновода с потерями

Из рис. 6 и 7 следует, что в ферритовой трубке с потерями поворот большой полуоси эллипса поляризации может происходить в различных направлениях в зависимости от частотного диапазона использования направляющей структуры (положительным считается поворот против часовой стрелки, если смотреть навстречу полю подмагничивания). При этом в низкочастотной и высокочастотной областях эксцентриситет эллипса поляризации близок к единице, что соответствует квазилинейной поляризации волны на выходе волновода. Увеличение длины волновода L приводит к уменьшению эксцентриситета эллипса поляризации. Как показали проведенные исследования, при большой длине волновода ( L > 1 м) в области частот, близких к частоте ферромагнитного резонанса, эллиптическая поляризация вырождается в круговую.

Полученные результаты позволяют сделать вывод о возможности использования круглого открытого слоистого феррит-диэлектрического волновода при построении различных СВЧ-уст- ройств: СВЧ-фильтров, работающих на основе явления комплексного резонанса [5], вентилей, фазовращателей, поглощающих аттенюаторов и т. п.