Диссипативность в одной системе прямого автономного управления

Получены достаточные условия ограниченности всех решений системы (А), (В) прямого управления при выполнении обобщенных условий Рауса — Гурвица (2).

Рассмотрим математическую модель объекта управления в виде системы xk    fk (uk),   k 1, 2,

(A)

где { x _O (t), x _o (t) } — вектор состояния объекта, { u _O (x _O ,x _O , t), u _O (x _O , x _o , t) } — неавтономный вектор управления.

Пусть движения x _k (t,t _o ,u^o), k = 1,2, u o = { u O (x o ,t _o ), uO(x ^o ,t _o ) } , x o = { x O ,x O } E R² = Ox1 x _o наблюдаются на промежутках I (t o ) = [t o , + ^ ) V t o >  0 при управлении вида:

{ u _O = ax _O + bx _O + P _O (t), u o = cx o + dx o + P o (t);

P k (t) = I P k (s)ds, k = 1, 2, t o

A = ad — bc = 0. (B)

При P k = 0 в работе [4] изучена абсолютная устойчивость системы (A).

В теории автоматического управления (регулирования) (ТАУ) (А), (В) называют системой прямого управления (регулирования) c двумя исполнительными органами f o (u o ) и f o (u o ) .

Для системы (А) с (В) решаем задачу анализа теории автоматического управления (ТАУ): найти область S изменения значений параметров a, b, c, d , свойства функций P k (t) в управлениях u _k , для которых система возмущения (А) диссипативна , то есть все ее решения при неограниченном возрастании времени t финально ограничены при любом выборе f _k , удовлетворяющих обобщенным условиям Рауса — Гурвица.

Если множество S не пусто, то управления (В) называют законом обратной связи или законом регулирования . Его реализация осуществляется с помощью совокупности измерительных приборов, усилителей, преобразователей и исполнительных устройств, называемых регулятором.

Определение области S осуществляем на основании прямого метода Ляпунова и некоторых качественных приемов исследования диссипативности динамических систем на плоскости, которые разработаны в работах [1–4].

В системе (А) перейдем от координат (x1,x2) к координатам (u1,u2); преобразование (В), осуществляющее этот переход, согласно Л = 0, является невырожденным. Новая система будет иметь вид j ui = afi(ui) + bf2(u2) + pi(t), [ u 2 = cfl(Ul) + df2(u2) + P2(t).

Система (1) является системой непрямого регулирования.

Будем предполагать, что функции f k (u k ), p k (t), k = 1, 2 удовлетворяют следующим условиям:

• I.    Непрерывные функции своих аргументов.

• II.    Функции p k (t) и их первоообразные P k (t) на полупрямой 0 <  t o <  t <  + то ограничены , то есть удовлетворяют для всех t ≥ t _o неравенствам:

| p k (t) | <  m, | P k (t) | <  M,k = 1, 2, m,M — const.

• III.    Cуществуют числа U k > 0 и функции e(u k ) > 0, k = 1, 2 такие, что в множестве

G = {(U1,U2) : |U1| >U0 |U2| >Uk} выполняются обобщенные условия Рауса — Гурвица:

J ah i (u i ) + dh2 (U 2 ) [Л x h i (u i )h 2 (u 2 )

< - £ ^{( u}1 ) ^— ^^(и 2 ),

> e(u i ) + 6^ 2 ),

^f k ^{( u} k ) h k (U k ) = ------- u k

| u k I >  U k ;     (2)

причем lim uks(uk)sgnuk = +w, k = 1, 2. |uk |→+∞

Пусть матрица B =

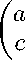
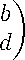
устойчива, то есть

Л = det B = ad — bc >  0 SpB = a + d <  0.

Замечание 1. Неравенства (3) — условия Рауса — Гурвица для двумерной линейной однородной системы x = Bx обеспечивают отрицательность вещественных частей собственных чисел матрицы B , согласно чего и условия II все решения линейной неоднородной системы зс = Bx + P(t), P(t) =

P 1 ( t )

P 2 ( t )

будут ограничены при t >  t o >  0 .

Замечание 2. Если функции f k (u k ) = u k , k = 1, 2 , то система (А) — линейная неоднородная система, и при выполнении условий Рауса — Гурвица (3) согласно замечанию 1 эта система диссипативна.

В дальнейшем будем считать c >  0 (в противном случае этого можно добиться заменой v _i = u _i , v ₂ = — u ₂ .) Согласно (3) возможны случаи:

• 1)    ad <  0 , откуда в силу А > 0 и c > 0 вытекает, что b <  0 ;

• 2)    a <  0 , d <  0 , → b <  ^a _c ^d , b — знаконеопределено .

Из (2) и (3) следует, что функции h k (u k ) при | u _k | > U O , k = 1, 2, одного знака. В случаe 1 , не умаляя общности, будем считать:

a >  0 , d <  0

(если a < 0, d > 0 , то, переименовав переменные u _i на u ₂ и u ₂ на u1, придем к тому же случаю).

В рассматриваемом случае из (2) следует, что в G функция h _i (u _i ) + ^(u1) ограничена сверху, а функция h ₂ (u ₂ ) + ^(U2) — снизу.

Положим:

c _i = sup

|u1 |>U ₁ ^o

hi(ui) + ^u2)}; c* = inf hh2(u2) + ^u2)} , 1 1 a             2     |u2 |>U2o     2 2 d откуда и из первого неравенства

в (2) следует, что в множестве G :

ac _i + dc2 <  0,

s(ui) hi < hi(ui) +-- a

< c i , ^c 2 <  ^h 2 ^(u 2 ) +--^^ <  ^h 2 ^{( u}2 ⁾ ,

причем, если c _i и с 2 достигаются, то ac _i + dc 2 < 0 , то есть из обобщенных условий Рауса — Гурвица (2) следует ограниченность сверху функции h _i (u _i ) при | u 1 1 >  U 0 и снизу функции h ₂ (u ₂ ) при | u ₂ | > U ₂ ^O .

Кроме того, в случае 1) будем предполагать ограниченность сверху функции h2(u2) при |u2| > U20, то есть имеет место неравенство h2(u2) < c2,     c2 = sup

|u2 |>U ₂ ⁰

Заметим, что в случае 2) это предположение выполняется автоматически при b >  0 .

Таким образом, из (2)–(4) и предположения (5) приходим к следующим нера- венствам:

h i (u i ) < c i

| u 1 | > U 1 ^o ,

| u 2 | > U 2 ^o ,

(5) i

c ^* ₂ < h 2 (u 2 ) <  c 2 ac i + dc2 <   0.

В рассматриваемом случае c 2 = 0 , ибо в противном случае при c * = 0 из (5) _i следует, что в G h i (u i ) < c i <  0, h 2 (u 2 ) > 0 , то есть функции h i (u i ) и h 2 (u 2 ) противоположных знаков, что противоречит условиям (2) и (3).

Не ограничивая общности, будем считать с 2 >  0 , тогда из (2) и (5) _i следует, что c _i > 0 и c ₂ > 0 [если c 2 < 0 , то из (5) _i вытекает, что c _i < 0 и c ₂ < 0 и, поменяв местами u ₁ и u ₂ , приходим к тому же случаю].

Лемма 1. Если при c. > 0 в множестве G выполняются обобщенные условия Рауса — Гурвица (2), (3) и (5), то имеет место нeравенство ci >hi(ui) >sx(ui)    |ui| >Uo,     £i = ^u^ > 0,            (6)

c.A при этом |hi(ui)ui| ^ +то при |u11 ^ +то.

Доказательство. В G второе неравенство в (2) перепишем в виде

2 ^{( U 1 )} (c . h i A) >  e(ui ).

c 2

Отсюда, учитывая, что 2 > c. > 0, и 0 < h2(2u2) < 1 при |u2| > U*, получим c.hi(ui)A > e(ui)     |ui| > UO.

Откуда и из (5) приходим к требуемому неравенству (6).

Таким образом, в рассматриваемом случае 1):

a >  0, d < 0, ci > 0, c 2 > 0| .

Теорема 1. Пусть выполняются условия I-III, (3), c > 0. Тогда в случае 1 условия: (5), aci + dc*. < 0(7)

(если c , c∗2 — достигаются ), fi(U) — 01^ > f (u0) — qu"    u” > u0 (|u0|, |<| >UO);(8)

f2(U) — c^Uy < f2(u?) — c^A    U2 > U2 (lUI, IU2I > UO)(9)

2  2     22     2  2     22      2     2     2    22

достаточны для диссипативности системы (1), а все движения системы (А) с неавтономным управлением ограничены при t ^ + то .

Доказательство. Введем в рассмотрение функцию

V i (ui,U 2 ) =

u1

A1

—    |hi(ui )|uidui +-(dui c2                       2

o

— bu . ) ² .

Заметим, что при | u 1 | > U ₁ ^o в силу леммы 1 | h 1 | ≡ h 1 . Поэтому

V(ui,u ₂ ) > 0 при u 2 + u . = 0.

В G полную производную функции V _i (ui,u ₂ ) в силу системы (1) можно представить в виде

A

• V i (ui,u 2 ) = c. hiu i [(ah i + dc ₂ )u i + p i ] + (du i — bu . )(dp i — bp . ).

Согласно лемме 1 существует U ₁ ¹ > U ₁ ^o такое, что при | u ₁ | > U ₁ ¹ выполняются неравенства:

| (ah i + dc 2 )u 1 | > ^2 + d^ m, b + d _   bc 2 + dc 2

| f i (u i ) | = | h i u i | >A" m >-- С”д— m (0 < C2 < C 2 ).

Тогда при | u _i | >  U i;, учитывая, что d <  0, b <  0,

| (ah 1 + dc 2 )u 1 + p _i | >  ^ "d ^ m.

Поэтому в первой четверти при u 1 > U ₁ ¹ , u > U ₂ ^o

I

V 1 <

— h _i u _i — | du _i — bu ₂ 1 (b + d)m < 0, c ₂ d

| du 1 - bu 2 | <

A

-

c ^∗ d

h 1 ^u 1 ^.

Рассмотрим при | u ₁ | > U ₁ ¹ функцию

^{( du}1

V 2 (U i ,U 2 ) = ----

-

bu2)2

,

для которой в силу системы (1) имеем

В силу выбора U ₁ ¹

При этом

при

I

V > (u i ,U 2 ) = (dui

-

bu 2 )[Ah i U i + dpi — bp 2 ].

Ah _i u _i + dp _i — bp ₂ >  Ah _i u _i + (d + b)m > 0.

V2(ui,u ₂ ) < 0    ui >  U ⁱ , (du _i — bu ₂ )u ₂ < 0.

Кроме того,

du2 dt ^<

ui >  U ⁱ , c 2 (du _i — bu ₂ )

> — "df i (u i ) — 2m.

В самом деле, выбирая U1 = max { U 0 ,N } ,

где

N = max sup |u1|≤U ₁ ¹

cfi(ui) + m

- dc ^∗ ₂

; inf ^{Cf i ( Ui}> ~ m I = |u1|≤U ₁¹      - dc ₂

c max dc∗2

sup ( fi ( ui |u1|≤U ₁ ¹

+ m); inf (fi(ui) — m)| , c    |u1|≤U11                c при u1 > U11 , u2 > U21 ddut2 представим и определим знак du2 dt

-

^d bC ₂ (du 1

1                  *

bu 2 ) + b [d(ah i + dc2 )u i + bp 2 ] + d(h ₂

-

^c 2 ^)u 2

-

A, h 1 ^u 1 ^<

b

<

- d

b

<

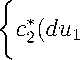
d

^- bu2) ^{- [(}ah i + dc2)^ui + bp 2 ^] + —^f 1 (u 1 ⁾ j-

<

b

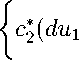
- bu2) + 2m + ^f i (u i ) |

< 0

в силу (11), то есть u ₂ (t) убывает в области (11).

В верхней полуплоскости плоскости 0u ₁ u ₂ при u1 < U ₁ ¹ ,u ₂ > U 1 вдоль траектории f (t,t ₀ ,q _o ) системы (1) u ₂ (t) также убывает, поскольку вследствие выбора U 1 при | u ₁ | ≤ U ₁ ¹ , u ₂ > U ₂ ¹

m u2(t) = fi(ui) + dfi(u2) < cfi(ui) + dc*U2 + m = dc* ( fi(ui) +--) < 0 c и при ui < -Uii < 0, u > U2i > 0

u ₂ (t) = ch ₁ u ₁ + dh₂u ₂ + p₂< 0     ch ₁ > 0, dc * < 0,

Ui l u 1 = o < af i (0) + bc2U2 + m <  0

при достаточно больших u ₂ . Поэтому траектория пересекает cправа налево положительную полуось 0u ₂ плоскости 0u ₁ u ₂ .

В полосе 0 < u ₂ < u 2 , где u2 — точка пересечения траектории u(t,t _o ,q _o ) с положительной полуосью ординат 0u 2

V 2 (U 1 ,U 2 ) < 0       | U 1 | .

В нижней полуплоскости рассуждения аналогичны.

Из дуг линий уровня функций V i (u ₁ ,u ₂ ), i = 1, 2 и отрезков прямых, u ₂ = C можно построить спирали L , раскручивающиеся против часовой стрелки и пересекаемые траекториями системы (1) в сторону начала координат (рис. 1).

Далее, рассуждая как при доказательстве теоремы 2.2 [3], покажем, что траектории системы (1) ограничены.

Допустим, что u(t, t _o ,q _o ) — произвольная траектория системы (1), проходящая при t = t o через точку q _o (u^^u^) , уходит в бесконечность при t ^ + ^ , образуя раскручивающиеся против часовой стрелки витки спирали L .

Пусть q ₁ mq ₂ , где q ₁ (0,u ⁰ ₂ ), q ₂ (0,u₂), u'2 > u ⁰ ₂ >  U2,, один из таких витков. Рассмотрим кривoлинейный интеграл

I =

I [af i (u i ) + bf2(u2) + P i (t)]du 2 - l

[cf i (u i ) + df2(u2) + P 2 (t)]du i ,

где l — замкнутый контур, образованный витком q ₁ mq ₂ и отрезком q ₁ q ₂ оси ординат 0u ₂ , и проходимый против часовой стрелки.

Так как интеграл I = 0 вдоль витка q1mq ₂ траектории u(t,t _o ,q _o ) , то считаем, что f 1 (0) = 0 (в противном случае этого можно добиться переносом начала координат).

u02

I = У bf2(u2)du2 + У P1(t)dU2 > --С- (u'22 u020

u02

- u22) + I P2(t)du2 >  У P2(t)du2 . (12)

u020

С другой стороны, I = I1 + I ₂ , где

I 1

= y[af i (u i ) + bf ₂ (u2 )]du 2

- [cfi(ui) + df 2 (u 2 )]du i ,

I 2

= У P i (t)du2

- p 2 ( t ) du 1 .

Применяя к I ₁ формулу Грина, получим

I 1

УУaf1 (ui) + df2 (u2)]dui du2, а вследствие условий (7)–(9) —

₄                                            u ⁰ 1

I <  (ac + dc 2 )S + I ₂ = (ac + dc* ₂ )S + X^ У p1(t)du ₂ — p ₂ (t)du 1 + У p1(t)du ₂ , i=1 _{li                                         u} 0 ₂ 0

где S — площадь области, ограниченной витком q 1 mq 2 , l i — части витка, лежащие внутри i -й четверти ( i = 1,.., 4 ).

Покажем, что для витка, достаточно удаленного от начала координат, неравенства (12) и (13) противоречат друг другу. Рассуждая как при доказательстве теоремы 1.3 [2; 3], из геометрических соображений видно, что наиболее неблагоприятным для доказательства является случай, когда вдоль рассматриваемого витка во второй (четвертой) четверти u 1 (t) все время убывает (возрастает), а в третьей (первой) — u ₂ (t) сначала убывает (возрастает).

Поэтому, если мы покажем, что в этом случае виток q 1 mq 2 не раскручивается против часовой стрелке, то в других случаях, когда вдоль витка, например, во второй (четвертой) четверти u ₁ (t) — не все время убывает (возрастает), он и подавно не может раскручиваться.

В рассматриваемом неблагоприятном случае во второй (четвертой) четверти u ₂ ( t ) будет монотонно убывать (возрастать). Поэтому справедливы следующие оценки:

У p i (t)du 2 — p 2 (t)du i <  — m(u min — u max ), (14) l2

У p 1 (t)du ₂ — p ₂ (t)du 1 <  — m(umax — u ^min ), (15) l4

где u min ,u min , umax , u max — суть наименьшие и наибольшие значения u _i (t) и u ₂ (t) на рассматриваемом витке.

Далее рассмотрим третью четверть и внутри нее кривые:

af i (u i ) + 6/ 2^2 ) + m = 0, (16)

af i (u i ) + bf2(^2) - m = 0, (17) cf i (u i ) + dMu) + m = 0, (18) cf i (u i ) + df2(u2) — m = 0. (19)

Согласно (3) и достаточной удаленности витка от начала координат эти кривые при u 1 <  - u ¹ ₁ расположены сверху вниз в порядке возрастания номера кривой (рис. 2).

U2

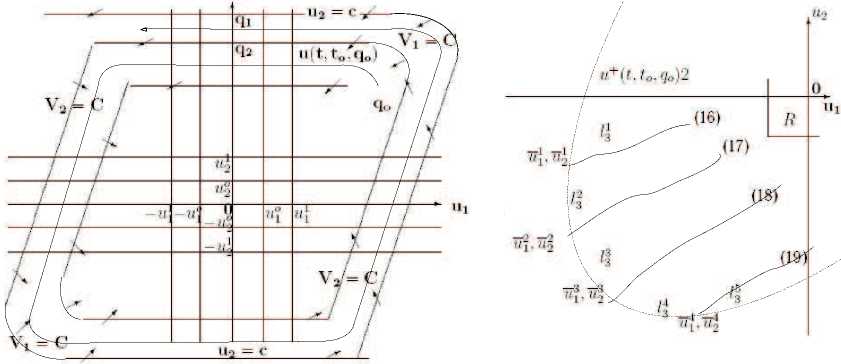
Рис. 1

Рис. 2

Вдоль траектории системы (1) абсцисса u _i (t) убывает выше кривой (16), где u 1 < af _i (u _i ) + bf ₂ (u ₂ ) + m <  0, возрастает ниже кривой (17), где u _i > af _i (u _i ) + +bf ₂ (u ₂ ) — M >  0; u ₂ (t) убывает выше кривой (18), где u ₂ < cf _i (u _i ) + df ₂ (u ₂ ) < 0 , и возрастает ниже кривой (19) ( u ₂ > cf _i (u ₂ ) + df ₂ (u ₂ ) > 0 ).

Следовательно, выше кривой (16) u _i (t) и u ₂ (t) возрастают; между кривыми (17) и (18) u _i (t) возрастает, а u ₂ (t) убывает.

Между кривыми (16) и (17), то есть внутри полосы cfi(ui) + df2(u2) + m = 0 cfi(ui) + df2(u2) - m = 0, где u2 (t) — убывает, имеет место неравенство du1     b du2    d

Между кривыми (18) и (19), где ui(t) — возрастает, du2

d

du ₁

Разбивая дугу 13 траектории в третьей четверти точками (ui ,иг2), i = 1,.., 4, лежащими соответственно на кривых (16)-(19), на части 13j), j = 1,..., 5, можно показать, что на этих дугах, где ui(t) и u2(t) изменяются монотонно, справедливы оценки:

IPi(t)du2 - p 2 (t)du i

I ⁽¹⁾

l3

< m[(u 1 - u 1 ) - u 2 ],

I Pi(t)du2 - P2(t)dui l3

< m[(u 3 - u i ) - (u 2 - u ³ )],

I Pi(t)du2 - P 2 (t)du i

, (5)

l ₃

, z—5          —4

< m(U 2 - U 2 ) - U i ,

(2)      (4)

а на дугах l ₃ и l ₃

IPi(t)du2 - P2(t)dui < i (2)

l ₃

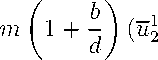
^- u 2 ),

IPi(t)du2 - P 2 (t)du i <

I (4)

l ₃

m

(¹ + d) ^{(u i}

^- u i ).

Вследствие этих оценок получим jpi(t)du2 -p2(t)dui < m l3

^d min

²⁺ b  ^{U i}

b

+ 2 + -d

min u ₂

Аналогично jpi(t)du2 - p2(t)dui < m l1

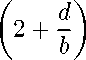
max u1

+

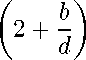
max u2

Объединяя (14), (15), (20), (21) вследствие (13), получим u2

I <  (ac _i + dc2)S + m

(U max

-

u

in ) + у

min

p i (t)dU 2 ,

u

//

где S — площадь области, ограниченной контуром l. Продолжая дословно рассуж-

дать как в теореме 1.3 гл. II [2], при достаточно большом u02, из (12) и (22) получим неравенства u2                               u2

I P i (t)du 2 < I < -e + IPi(t)du2, u ₂ ⁰                                     u ₂ ⁰

которые противоречат друг другу.

Следовательно, для достаточно большого u ⁰ ₂ виток q ₁ mq ₂ не может раскручиваться против часовой стрелки при возрастании t . Отсюда следует, что траектории системы (1) ограничены при t ^ + ^ .

Дальше доказывается, что каждая траектория системы (1) при t ^ + то попадает в некоторую ограниченную область и там остается при дальнейшем возрастании времени t , то есть система (1) диссипативна. Что и требовалось доказать в рассматриваемом случае.

В случае 2: a <  0 , d <  0 , обобщенные условия Рауса — Гувица запишем в виде

J ah i (u i )+ dh 2 ⁽u 2 ⁾<  — 6(u i ),                f k (u k )               o_

, h k ^{( u} k ) =                | u k | >  ^U k ;      ⁽²²⁾

A x hi(ui)h2(u2) > s(ui),                    Uk причем lim u1e(u1)sgnu1 = +^.

| u 1 |→+∞

Откуда в рассматриваемом случае из первого неравенства в (22) следует, что h k (u k ) > 0 при | u k | > U 0 , k = 1,2 .

Лемма 2. Если с > 0 ив G выполнены условия (22), то в случае 2 существует число с2 > 0 такое, что f hi(ui) >> Е*1 |ui| > Uf,

Ih2(u2) > ^2    |U2| >Uf , где

*     ^^(u 1 )

е1 = ~^: C2 = inf h2 (U2), 1    c2A     2   Ы>и2° причем e1(u1) > e1(u1) и c2> > c2.

Доказательство. В рассматриваемом случае из (23) следует, что h _k (u _k ) > 0 при | u k | >U f ,k = 1, 2.

Полагая с2 = inf h2 (U2), 2 |u2|>U2o в силу h2(u2) > 0 при |u2| > UO имеем c2 > 0.

Допустим, что с 2 = 0. Тогда существует последоватeльность чисел { u 2 } ( | u 2 | >  U₂ ), i = 1,2,... , такая, что при i ^ + то h ₂ (u 2 ) ^ 0 . Поэтому для каждого фиксированного u1 ( | u 1 1 > U f ) и достаточно большого i

Ah 1 (u 1 )h 2 (u ⁱ ₂ ) <

e(ui)

Но вследствие обобщенных условий Рауса — Гурвица (23) при выбранных u ₁ и i

Ah i (u i )h 2 (u i₂ ) > e(u i ),                                 (25)

что противоречит (24). Полученное противоречие показывает, что в случае 2 с 2 > 0 .

Далее, пeреходя в (25) к пределу при i → ∞ , получим неравенство

Ah1(u1)e > e(u1), откуда следуют неравенства (23), причем е1 > £1, так как c2 > с2 > 0. Лемма доказана.

Теорема 2. Если c >  0 , то в случае 2: a <  0, d < 0 , достаточны для диссипативности системы (1).

условия I–III, (2), (3) и (5)

Доказательство. 1. Пусть b>0 . В этом такое, что

подслучае в

силу (23) выбрать U ₁ ¹ > U ₁ ⁰

du ² ₁ dt

< 0

в областях поскольку при

u ₁ <  - U ₁ ¹ ,

^u 2 ≥

-

^U 2 ^o

u 1 > U ₁ ¹ ,

u 2 ≤ U ₂ ^o ,

| u 1 | > U ₁ ¹ ,

| u 2 | ≤ U 2 ^o

в силу | u 1 (u 1 )u 1 | >

bH+m _, где

-a

H = sup | f ₂ (u ₂ ) | при | u ₂ | <  U O , имеем

а при

имеем

в силу выбора U ₁ ¹ и дает область (26).

du ² ₁ dt

< | u i | (a | h i U 1 | + b | f 2 (u 2 ) | + m) < 0,

u i > U i , u 2 < - U o u 1 <  - U ₁ ¹ , u 2 ≥ U ₂ ^o

du ²

-t^ <  -| u i | bH < 0

bh ₂ (u ₂ ) > 0 при | u ₂ | >  U20. Объединение областей (27) и (28)

Далее в силу выбора U ₁ ¹ и U ₂ ¹ (см. с. 49)

du ²

-d² = U2(chiUi + dh 2 U 2 ) < 0

в областях

Кроме того,

u 1 ≤ U 11 ,	U 2 > U 21 ;	(29)
u 1 >  - U 1 1 ,	u 2 <  - U 2 1 .	(30)
dV (U 1 ,U 2 ) < 0 при
U-U2 > 0,    | U 1 1 >	U 11 ,     | u 2 | > U 2 o .	(31)

Объединение областей (26), (29)–(31) содержит R ^C (дополнение R ), где

R = { (U 1 ,U 2 ) : | U 1 1 <  U 1 , Ы^¹} -

Поэтому из отрезков прямых u1 = C, u ₂ = C, V 2 (u 1 ,u ₂ ) = C можно построить семейство замкнутых кривых L , которые охватывают прямоугольник R и пересекаются траекториями системы (1) в сторону начала координат (рис. 3).

2. Пусть b<0 . В силу выбора U ] 1 >  U O , k = 1, 2

V ₂ (u 1 , u ₂ ) < (du1 — bu ₂ )[Ah ₁ u ₁ — (d + b)m] < 0

в областяx u1 u ₂ < 0, | u 1 1 > U 1¹ , | u ₂ | > U 2O ;

du ² < 0 при | u 2 1 >  U1 ; du i < 0 при u . <

-

U ₁ ¹ , u 2 ≤ U ₂ ^o и u 1 > U ₁ ¹ , u 2 ≤ - U ₂ ^o .

Это позволяет из отрезков прямых V2 = C, u1 = C, u ₂ = C, лежащих в R C , также построить семейство замкнутых кривых (рис. 4), как и в предыдущем случае.

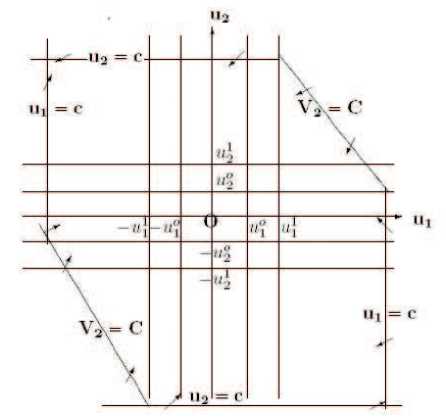
Рис. 3

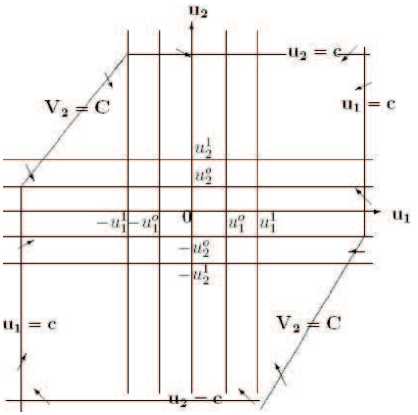
Рис. 4

• 3. Пусть b=0 . Вследствие (23) и e > 0

• 1    du 1     e(u 1 )

1^- <      u i + m u .    ^ ^    | u i | >U.

• 2    dt      dC2

Кроме того, в силу d < 0, С 2 > 0 и непрерывности функции f ₁ (u ₁ ) в любой полосе | u 1 | < C , где C > U ₁ ^o и достаточно больших | u 2 | ,

2du ² <ЫНЛЫ 1 + dc2 + m] < 0.

Тогда из отрезков прямых u1 = C, u ₂ = C можно построить прямоугольник L , окружающий множество R и пересекаемый траекториями системы (1) в начала координат плоскости 0u1u ₂ .

Далее во всех разобранных подслучаях b >  0 и b <  0 вводим в рассмотрение функцию V(u 1 ,u ₂ ), такую, что V(u 1 ,u ₂ ) = а > 0 тогда и только тогда, когда точка (u 1 ,u ₂ ) Е L , где L проведена через точку (0,а) . Очевидно, эта функция определена, непрерывна и положительна в R^c , причем V(u 1 , u ₂ ) ^ + то при u. + u 2 ^ + ^ .

Вдоль траекторий системы (1) функция V(u 1 (t),u ₂ (t)) монотонно убывает , так как траектории системы пересекают L снаружи внутрь и нигде не касаются ее, что следует из способа построения кривой L .

Таким образом, выполнены все условия теоремы 2.4 из работы Ю.Н. Бибикова [3]. Продолжимость решений системы (1) cледует из существования замкнутой кривой L .

Теорема 2 доказана.

Замечание 3. Если в управлениях u k (x1,x ₂ ,t), k = 1,2 функции P _k (t) имеют период ω по t , то при выполнении условий диссипативности теорем 1, 2 система (1) ((А)) имеет хотя бы одно ω -периодическое решение (движение).