Дизайн и изготовление зеркала с поверхностью свободной формы для формирования постоянной освещённости в прямоугольной области

Задача расчёта преломляющей или отражающей оптической поверхности из условия формирования заданного распределения освещённости в некоторой области относится к классу обратных задач неизображающей оптики и является крайне сложной. В большинстве случаев данная задача сводится к решению нелинейного дифференциального уравнения (НДУ) эллиптического типа (обобщённого уравнения Монжа–Ампера) [1 –7]. Решение этого НДУ является сложной теоретической и вычислительной задачей.

Формулировка обратной задачи расчёта оптической поверхности как задачи решения НДУ предполагает, что рассчитываемая поверхность является гладкой. Это накладывает ряд ограничений на класс распределений освещённости, которые могут быть сформированы этой поверхностью. Например, гладкая оптическая поверхность не позволяет сформировать распределение освещённости, определённое в несвязной области, состоящей из непересекающихся подобластей. Ограничения также возникают и при формировании многосвязных областей и областей со сложными негладкими границами.

Ряд обратных задач расчёта оптических поверхностей может быть сформулирован в виде задачи Монжа–Канторовича о перемещении масс (ЗПМ) со специальной функцией стоимости [8– 19]. Данная ЗПМ описывает задачу расчёта лучевого отображения (т.е. отображения, связывающего координаты падающих на оптическую поверхность лучей и координаты преломлённых (отражённых) лучей в освещаемой области), которое обеспечивает формирование заданного распределения освещённости. При этом восстановление оптической поверхности по лучевому отображению эквивалентно задаче восстановления функции по её полному дифференциалу. «ЗПМ-формулировка» задачи имеет ряд преимуществ и, например, в отличие от задачи решения НДУ позволяет рассчитывать непрерывные кусочно-гладкие оптические поверхности, формирующие требуемые распределения освещённости в несвязных областях и в областях со сложными и негладкими границами [16– 19].

В работах ряда авторов данной статьи было предложено осуществлять расчёт лучевого отображения непосредственно через решение ЗПМ [15– 19]. Для этого ЗПМ записывается в дискретной форме как линейная задача о назначениях (ЛЗН) [20]. Хорошие рабочие характеристики такого «ЛЗН-подхода» были продемонстрированы для различных задач расчёта оптических элементов. Тем не менее, в известных работах не было представлено результатов экспериментальной верификации ЛЗН-подхода.

В настоящей работе представлены первые экспериментальные результаты по изготовлению и исследованию зеркала свободной формы, рассчитанного в рамках ЛЗН-подхода и предназначенного для формирования постоянной освещённости в прямоугольной области. Результаты экспериментальных исследований находятся в хорошем соответствии с результатами численного моделирования и подтверждают «технологичность» использованного метода расчёта.

1. Метод расчёта зеркал на основе решения линейной задачи о назначениях

Геометрия задачи расчёта зеркала для формирования заданного распределения освещённости показана на рис. 1. Излучение от точечного (компактного) источника O падает на зеркало. Задача состоит в расчёте поверхности зеркала, обеспечивающего формирование в области D в плоскости x = f 0 заданного распределения освещённости E . Под освещённостью понимается световой поток, падающий на единицу площади.

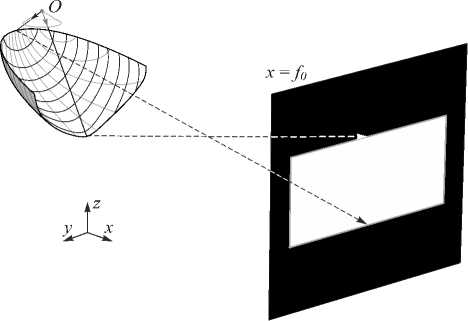
Рис. 1. Геометрия задачи расчёта зеркала

В рассматриваемой задаче считается выполненным условие дальней зоны. Это условие означает, что размерами зеркала, по сравнению с расстоянием до плоскости x = f 0 , можно пренебречь. В этом случае зеркало можно рассматривать как точечный источник О' , т.е. считать все отражённые от зеркала лучи выходящими из одной точки. Будем считать, что излучение точечного источника O описывается функцией интенсивности I , заданной в некоторой области G на единичной сфере. На рис. 1 источник излучает в пределах некоторого конуса. Под интенсивностью понимается световой поток, излученный источником в единицу телесного угла.

Преобразование светового потока от источника излучения О, происходящее при отражении падающих лучей от поверхности зеркала, можно описывать как отображение области G в область D. Причём это «лучевое отображение» (т.е. отображение, определяющее координаты точек пересечения отражённых лучей с плоскостью x = f0 через координаты падающих лучей из области G) удовлетворяет закону сохранения светового потока. В базовых теоретических работах [8, 9] показано, что в рассматриваемой задаче расчёта зеркала расчёт лучевого отображения может быть сведён к решению задачи Монжа–Канторовича о перемещении масс (ЗПМ) с неквадратичной функцией стоимости. Под исходным и финальным распределениями масс в данной ЗПМ понимаются распределение интенсивности I точечного источника, заданное в области G на единичной сфере, и требуемое распределение освещённости E, заданное в области D. Функция стоимости «перевозки» единицы массы (единицы светового потока) из области G в область D является известной [8, 9].

В работах ряда авторов данной статьи предложено осуществлять расчёт лучевого отображения непосредственно через решение ЗПМ [15– 19]. Для решения ЗПМ она записывается в дискретной форме как линейная задача о назначениях (ЛЗН). При этом используется следующий подход. Области G и D аппроксимируются N ячейками с одинаковой «массой» (с одинаковым световым потоком). В этом случае все отображения G ^ D , сохраняющие световой поток, можно описать перестановками из N чисел, которые определяют, в какие ячейки области D отображаются ячейки области G . В рамках ЛЗН отображение ячейки области D с номером i в ячейку области G с номером j можно интерпретировать как выполнение i -м работником j -й работы. При этом стоимость выполнения работы определяется известной функцией стоимости «перевозки» [8, 9]. Отметим, что для решения ЛЗН известны различные эффективные алгоритмы (венгерский алгоритм, алгоритм Джонкера – Волгенанта, алгоритм аукциона), решающие задачу за полиномиальное время.

В рамках используемого «ЛЗН-метода» поверхность зеркала рассчитывается через лучевое отображение, которое находится из решения ЛЗН. Для этого поверхность зеркала записывается в виде огибающей двухпараметрического семейства параболоидов вращения, у которых положения фокусов совпадают с точечным источником О , а направления осей задаются радиус-векторами точек области D . При таком представлении поверхности зеркала отражённые от зеркала лучи будут приходить в область D . При выбранном представлении поверхность зеркала определяется через «фокальную функцию», равную фокусным расстояниям параболоидов семейства. Данная функция определяет формируемое зеркалом распределение интенсивности в области D . Для расчёта фокальной функции используются уравнения огибающей поверхности, сводящие расчёт фокальной функции к задаче восстановления функции по её полному дифференциалу.

С использованием описанного ЛЗН-метода было рассчитано зеркало для формирования постоянной освещённости в прямоугольной области с угловыми размерами 30°*15°, расположенной в удалённой плоскости x = f0. Расчёт производился для источника, излучающего по закону Ламберта в пределах кругового конуса с углом при вершине 160° (данный конус схематично показан на рис. 1). Рассчитанное зеркало показано на рис. 2а и имеет размеры 38,2×41,4×26,8 мм3. Отметим, в случае дальней зоны зеркало может быть промасштабировано требуемым образом, т.е. радиус-векторы точек поверхности зеркала относительно точки положения источника могут быть умножены на некоторый коэффициент для получения требуемых габаритных размеров. На рис. 2б показано распределение освещённости, формируемое зеркалом в удалённой плоскости x = 3000 мм. Данное распределение было рассчитано созданными авторами статьи программными средствами, реализующими метод трассировки лучей. При расчёте распределения использовались 1000000 лучей. Рис. 2б показывает формирование фактически постоянной освещённости в области заданных размеров. Для верификации выполненных расчётов работа зеркала также была промоделирована в коммерческой программе для светотехнических расчётов TracePro [21]. Результаты моделирования приведены на рис. 3 и также показывают формирование равномерного прямоугольного распределения.

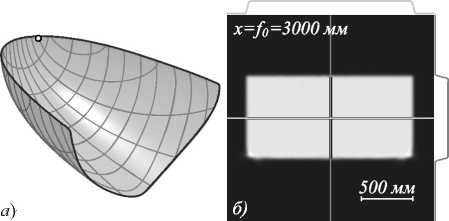
Рис. 2. Зеркало для формирования постоянной освещённости в прямоугольной области с угловыми размерами 30°×15° в удалённой плоскости (точкой отмечено положение источника) (a); рассчитанное распределение освещённости, формируемое зеркалом в плоскости х=3000 мм (б)

модели было произведено дополнительное сглаживание поверхности зеркала (аппроксимация рациональными B-сплайнами с точностью 0,015 мм), чтобы выполнить технологические требования. Для полученной CAD-модели на рис. 4 минимальный радиус нормальной кривизны составляет 3,18 мм. Отметим, что сглаживание поверхности приводит к ухудшению качества формируемого зеркалом распределения освещённости (нормированное среднеквадратическое отклонение формируемого распределения освещённости увеличивается с 5 % (рис. 2 б ) до 9%).

а)

Мт:9.31:Че-021. Mrn:).im Ave:0.23627

Total Flux:0.94508 И; Flux/Emitted Flux:0.94508, 945348 Incident Rays

б)

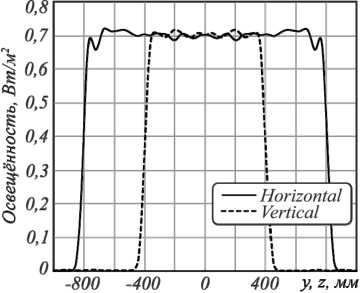
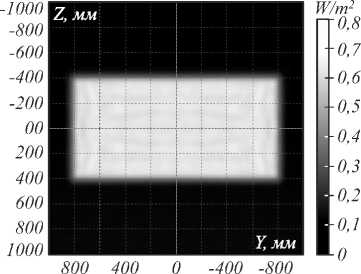
Рис. 3. Рассчитанное в программе TracePro распределение освещённости, формируемое зеркалом при точечном ламбертовском источнике (излучаемый поток 1 Вт)

в удалённой плоскости х=3000 мм (а); центральные сечения рассчитанного распределения (б)

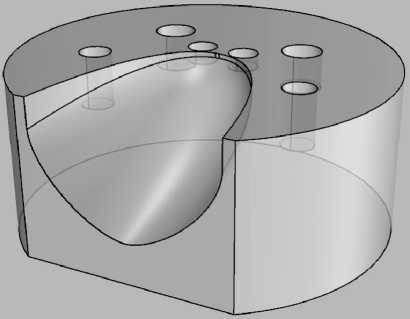
Рис. 4. CAD-модель зеркала

В последующих экспериментальных исследованиях зеркало, рассчитанное для точечного источника излучения, будет использоваться с реальным протяженным источником излучения в виде светодиода. Поэтому в программе TracePro было выполнено моделирование работы сглаженного зеркала при размерном источнике в виде светодиода Cree XP-C, имеющего размер 3,45×3,45 мм2 и приблизительно ламбертовскую диаграмму излучения. Результаты моделирования показаны на рис. 5. Распределение на рис. 5, по сравнению с распределением на рис. 3, является более неравномерным. Эта неравномерность, в частности, обусловлена размерами светодиода. В рассматриваемом примере минимальное расстояние от светодиода (размер 3,45×3,45 мм2) до поверхности зеркала составляет всего 5,6 мм. Поэтому в данном случае светодиод нельзя считать точечным источником. Несмотря на это, формируемое зеркалом распределение является достаточно хорошим и подтверждает «устойчивость» рассчитанного зеркала к вариациям размера источника и диаграмме излучения, которая лишь приближённо соответствует ламбертовскому закону излучения.

-1000 -800 -600 -400 -200

О 200 400 600 800 1000

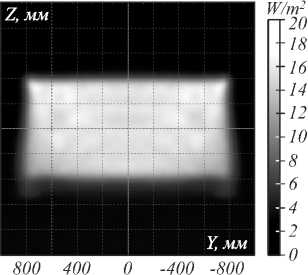
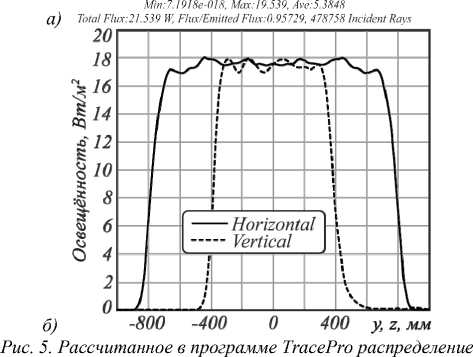
освещенности, формируемое сглаженным зеркалом в удалённой плоскости х=3000 мм при протяжённом источнике в виде светодиода Cree XP-C (излучаемый поток 22,5 Вт) с размером 3,45×3,45 мм ² (а). И центральные сечения рассчитанного распределения (б)

На основе созданной CAD-модели (рис. 4) была составлена программа в автоматизированной системе, предназначенной для подготовки управляющих программ для станков с ЧПУ. Такая программа содержит информацию о траекториях движения режущего ин- струмента и прочие параметры станка, необходимые для фрезеровки заготовки и получения спроектированной модели рассчитанного зеркала.

Далее зеркало было изготовлено методом фрезеровки на трёхосевом обрабатывающем центре Haas Minimill. При фрезеровке использовались прецизионные цилиндрические и сферические фрезы японского производителя Kyoсera. В качестве заготовки для зеркала использовалась дюралюминиевая плита (сплав Д16Т). Изготовленное зеркало показано на рис. 6 а . Для удаления следов фрезы выполнялась предварительная абразивная обработка полученной поверхности гибкими абразивами с размером зерна от 7 до 10 мкм. Для получения зеркальной поверхности оптического качества выполнялась финишная полировка войлоками с нанесённой алмазной пастой с постепенным снижением размера зерна от 7 мкм до 0,1 мкм. Фотография зеркала после финишной полировки приведена на рис. 6 б .

б)

а)

Рис. 6. Фотографии изготовленного зеркала до полировки (а) и после полировки (б)

3 . Экспериментальное исследование работы зеркала

Для измерения распределения освещённости, формируемого изготовленным зеркалом, использовался гониофотометрический стенд. Стенд включает в себя две прецизионные поворотные платформы, для задания ориентации зеркала с точностью 1 угловая минута по зенитному и азимутальному углам. Для оценки световых характеристик использовался люксметр Testo 545, измеряющий освещённость с разрешением 1 люкс и расположенный на некотором расстоянии от зеркала. Это расстояние должно быть выбрано таким образом, чтобы изготовленное зеркало вместе со светодиодом можно было считать точечным источником света. Для сравнения результатов измерения с результатами численного моделирования (рис. 5) расстояние было выбрано равным 3000 мм.

На рис. 7а представлены измеренные центральные сечения формируемого зеркалом распределения. Отметим, что при построении графиков учитывался перевод из угловых координат в декартовые. Измеренные значения освещённости нормированы на максимальные значения и отмечены окружностями, которые для наглядности соединены непрерывными линиями. Угловое расстояние между измеренными зна- чениями составляет 1°. Для сравнения на рис. 7а также показаны графики центральных сечений, полученные при численном моделировании (см. рис. 5б). Из рис. 7a видно, что результаты экспериментальных измерений находятся в хорошем соответствии с результатами численного моделирования. Для визуального контроля равномерности полученного светового распределения было получено изображение светового пятна на экране, расположенном на расстоянии 3000 мм от зеркала (рис. 7б). Изображение полученного пятна также визуально похоже на результат численного моделирования распределения освещённости на рис. 5. Таким образом, представленные результаты экспериментальных исследований находятся в хорошем соответствии с результатами численного моделирования.

б)

Рис. 7. Измеренные нормированные профили распределения освещённости в двух центральных сечениях

a)

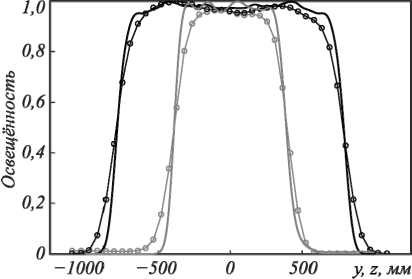
(линии с окружностями) и профили, полученные численным моделированием (непрерывные линии) (а); фотография формируемого зеркалом светового пятна на удалённом экране (б)

Заключение

С использованием ЛЗН-метода было рассчитано зеркало для формирования постоянной освещённости в прямоугольной области с угловыми размерами 30 ° х15 ° , расположенной в удалённой плоскости. Зеркало изготовлено методом фрезерования. На гонио-фотометрическом стенде измерены распределения освещённости в центральных сечениях формируемого зеркалом светового пятна. Результаты экспериментальных исследований находятся в хорошем соответствии с результатами численного моделирования. Это показывает технологическую реализуемость зеркал, рассчитанных ЛЗН-методом, с помощью технологии трёхосной фрезеровки. Полученные результаты могут найти применение при создании различных освещающих и прожекторных устройств.

Работа выполнена при поддержке Российского научного фонда (проект № 18-19-00326) в части расчёта, изготовления и исследования зеркала в оптиче- ском эксперименте и Министерства науки и высшего образования РФ в рамках выполнения работ по Государственному заданию ФНИЦ «Кристаллография и фотоника» РАН (соглашение № 007-ГЗ/Ч3363/26) в части численного моделирования работы зеркала.