Длинные волны в прямоугольном стенде, вызванные пластиной
Автор: Трепачв Виктор Владимирович
Журнал: Advanced Engineering Research (Rostov-on-Don) @vestnik-donstu
Рубрика: Физико-математические науки
Статья в выпуске: 6 (67) т.12, 2012 года.
Бесплатный доступ
Проведено исследование формы поверхности тяжёлой жидкости в прямоугольном волновом стенде, покрытой длинными волнами над ровным дном. Волны вызваны горизонтальными гармоническими колебаниями волнопродуктора щитового типа. Получено точное решение краевой задачи с учётом диссипации энергии в жидкости. Результаты применимы для расчёта и лабораторного моделирования поверхностных и акустических волн.
Тяжёлая несжимаемая жидкость, волнопродуктор, гармонические волны, длинные поверхностные волны, волновой стенд, диссипация энергии
Короткий адрес: https://sciup.org/14249902
IDR: 14249902 | УДК: 532.593
Текст научной статьи Длинные волны в прямоугольном стенде, вызванные пластиной
Введение. При рассмотрении теории длинных волн на поверхности тяжёлой жидкости можно в первом приближении пренебречь вертикальным ускорением частиц жидкости, это приводит к тому, что давление в жидкости практически равно статическому давлению, а скорость движения её частиц является функцией, которая не зависит от вертикальной координаты [1], [2]. Постановка задачи о волнах гармонического вида на мелкой воде в прямоугольном бассейне здесь сводится к рассмотрению краевой задачи в прямоугольнике для уравнения Гельмгольца [3], используемого в акустике. Траектории колебательного движения частиц жидкости представляют собой фактически отрезки прямых линий, параллельных дну бассейна. Наличие дна в таких условиях движения частиц вызывает дополнительное рассеяние энергии, учитываемое нами в рамках теории Рэлея [1]—[5]. Данная работа дополняет результаты [1]—[5] и других исследований, т. к. в ней учитываются не только эффекты конечности всех размеров волнового стенда, но также эффекты диссипации энергии волн, наблюдаемые в ряде натурных экспериментов для волновых полей в океане [2].
Постановка задачи. Рассмотрим гармонические волновые колебания несжимаемой, тяжёлой жидкости под ровным дном в прямоугольном бассейне, имеющем длину l , ширину 2b и глубину h. Опустим множитель eiωt , где ω — частота, t — время, i — мнимая единица. Постановка краевой задачи в линейном приближении теории длинных волн имеет вид д2ф|дx2 + д2ф/дz2 + k2ф = 0 ; k = ^(to2 - /pto) jgh ; p > 0;(1)
дф/дz = 0, z ■ b , 0 < x < l; Re k > 0 ; Im k < 0;(2)
дф/дx = 0 , |z| < b, x = l; l > 0, b > 0 ;(3)
дф/дх = u (z), |z| < b, x = 0; c = Tgh,(4)
где ф ( x , z ) — потенциал скорости, k — волновое число, p — коэффициент трения о дно, g — ускорение свободного падения, c — скорость длинных волн, x — продольная координата, z — поперечная координата, u ( z ) — амплитуда колебаний пластины волнопродуктора на плоскости передней стенки x = 0.
Построение решения . Решение краевой задачи (1)—(4) отыскиваем в виде функционального ряда с неизвестными коэффициентами A m , но который удовлетворяет краевым условиям (2), (3) и имеет вид да
Ф ( x, z ) = £ A m ( е /X m i ■ e X m x + е -1X m x ) cos [ y m ( z - b ) ] , (5)
m = 0
где y m = m n/2 b , а волновые числа х m продольных волн в (5) равны
X m = V к 2 - Y2 = ^(ш2/ с2 - m 2п/ ( 2 b ) 2) - / jw/ с 2 , с = gh. . (6)
Подкоренное выражение в (6) имеет разрез на отрицательной части действительной оси.
Решение в виде (5) удовлетворяет также и волновому уравнению (1). Коэффициенты Am находятся из краевого условия (4), которые представим соотношением да
U ( z ) = ' £ X m A m ( e /X m li " 1 ) cos [ Y m ( z - b ) ] , Y m = m n/2 b . (7)
m = 0
Система тригонометрических функций cos [ y m ( z - b ) ] попарно ортогональна на отрезке | z | < b , поэтому коэффициенты A m в случае m > 1 равны выражениям b
Am = ( '/ ( 1 - e ^ ”" ) X m b ) J U ( z ) C0S Y m ( z - b ) dz , Re ( X m ) > 0, Im ( X m ) < 0. (8)
-
- b
Подставим (8) в (5), получим точное решение краевой задачи о длинных волнах в прямоугольном бассейне (1)—(4).
Форма свободной поверхности n ( x , z ) выражается через потенциал скорости
П ( x , z ) = ( ( - / to + j )/ g ) ф ( x , z ) . (9)
Коэффициенты Am имеют смысл амплитудных множителей поверхностных волн. Коэффициент A 0 описывает амплитудный множитель «поршневой» волны. «Поршневая» волна имеет постоянное значение амплитуды вдоль направления оси z b
A, = ( ij ( 1 - e -2 kl ) 2kb ) J u ( z ) dz . (10)
- b
Если u ( - z ) =- u ( z ) , т. е. в случае нечётной по z амплитуды колебаний вибратора, то всегда амплитуда колебаний «поршневой» волны (10) имеет значение ноль. Можно подобрать вид чётной функции для амплитуды колебаний u ( z ) , при которой амплитуда колебаний «поршневой» волны равна нулю. Амплитуда колебаний «поршневой» волны отлична от нуля, если мгновенный расход жидкости q , вытесняемый вибратором в горизонтальном направлении, отличен от нуля
b q = h J u (z) dz * 0. (11)
- b
«Поршневая» волна распространяется по кратчайшему пути, соединяющему плоскость вибратора x = 0 и плоскость задней стенки бассейна x = l . Согласно (5) и ограничениям (8), построенное решение допускает предельный переход к бесконечной длине стенда l . В случае бесконечной длины стенда l в решении (5) присутствуют только волны, бегущие в одном направлении.
Бегущие волны в направлении от волнопродуктора к задней стенке стенда называют падающими. Падающая волна определяется вторым слагаемым в круглой скобке формулы (5). В случае конечной длины волнового стенда l возникает отражённая волна от задней стенки бассейна, занимающей положение x = l. Амплитудный коэффициент отражённой волны описывает- ся первым слагаемым в круглой скобке формулы (5). Он содержит параметр l . Предельный переход к бесконечной длине стенда l возможен при коэффициенте трения о дно р > 0.
Анализ волнового поля в стенде. Процесс возбуждения бегущих волн в волновом стенде возможен благодаря диссипации энергии. Рэлей предложил способ избавиться от паразитных свободных волн введением диссипативных сил, которые пропорциональны скоростям частиц жидкости [1]. В ряде работ, выполненных Вапняр Д. У., Михайловым Э. Н., Шапиро Н. Б., горизонтальный обмен количеством движения учитывается путём введения диссипативной массовой силы, которая пропорциональна горизонтальной скорости течения. Коэффициент трения μ позволяет [2] рассчитывать горизонтальный турбулентный обмен течений и внутренних волн в экваториальной зоне океана.
В монографии [2] приведены натурные оценки коэффициента трения μ в пределах от 10 -7 сек -1 до 10 -5 сек -1. Известно, что в мелководных районах моря отмечена связь коэффициента трения и угловой частоты колебаний. В лабораторных испытаниях волнопродукторов поверхностных и внутренних волн, проводимых с участием автора данной статьи, отмечена высокая эффективность применения такой модели с использованием частотной зависимости коэффициента трения от масштаба волн. Отражённая волна имеет больший пробег, чем падающая волна, поэтому в волновом стенде достаточно большой длины создаются условия её подавления.
Пусть скорость движения пластины вибратора u ( z ) чётная функция следующего вида
π
u (z ) = и0cosY1 z, Y1 = 2b, где u (±b) = 0.
Используя (8), (10), находим коэффициенты разложения потенциала скорости (5):
u e ikl
A = ---07 ; , Am 1 = 0 , m ^ 1 , Am
nsin ( kl ) k 'm — 1 , ,^ m
В отсутствии диссипации, т. е. в случае р = 0
—
iχ2ml u0
sin ( Х 2 m l ) X 2 m b
•
γ1
γ2 2 m
—
γ1 2 .
ω ω ω2 m 2π2
k =^ = 7 , X m = J 2 — 7^, Р = 0, V gh c cc ( 2b )
где k — действительное положительное число, называемое волновым числом «поршневой ны». «Поршневая волна» распространяется вдоль направления оси x . Появление волн, пространяющихся под острым углом к оси z , описывает условие излучения таких волн ω mπ k = — > Try-, Р = 0, m = 1,2,...,M , c 2b где M — число волн, полученных под углом к оси x . Угол излучения αm равен mπ am = arcsin——, m = 1,2,...,M , р = 0.
m 2 bk
вол-рас-
Чем больше ширина стенда 2 b , тем большее количество волн M сможет излучаться под углом к оси x . Чем больше значение номера волны m , тем больше её угол наклона α m в (16). В случае k = mn/2b угол наклона становится наибольшим и принимает значение, равное п/2. Упругие волны, распространяющиеся в плоском слое, изучались в [3] применительно к проблеме использования слоя в качестве волновода акустических волн.
При отсутствии диссипации энергии р = 0 возможны резонансные явления, связанные с конечностью длины стенда l . Тригонометрическая функция, находящаяся в знаменателе коэффициента разложения потенциала скорости (13), обращается в ноль при выполнении условий
k, = — = i n / l , i = 1,2,..., р = 0; i c
ω2 2 2
"Г — тП" = j 1/ 1 , j = 0,1,2,..., т = 1,2,..., M , P = 0.
c 2 2 b
При частотах колебаний, определённых в (17) и (18), возникают резонансы с бесконечной амплитудой колебаний. В постановке задачи присутствует диссипация энергии р * 0, которая не допускает возникновение резонансов с бесконечной амплитудой колебаний для распространяющихся волн, что дополняет известные результаты из теории плоских волн в волновом стенде [1].
Рассмотрим условие, которое противоположно по смыслу условию (15)
k
π
2 b
или
ωπ — < —. c 2 b
При выполнении (19) волны, распространяющиеся под углом к оси x , не излучаются. Соответственно резонансы типа (18) невозможны. При выполнении (19) колебания формы поверхности жидкости состоят из одной «поршневой волны» и счётного набора нераспространяющихся волн [3]—[5]. На рисунке 1 изображена поршневая мода колебаний на оси волнового канала с учётом диссипации энергии.
Под нераспространяющейся волной понимается волна, которая и в отсутствии диссипации энергии имеет амплитуду, убывающую по экспоненциальному закону. Нераспространяющиеся волны локализуются в некоторой окрестности волнопродуктора. При этом они быстро затухают в направлении движения от волнопродуктора.
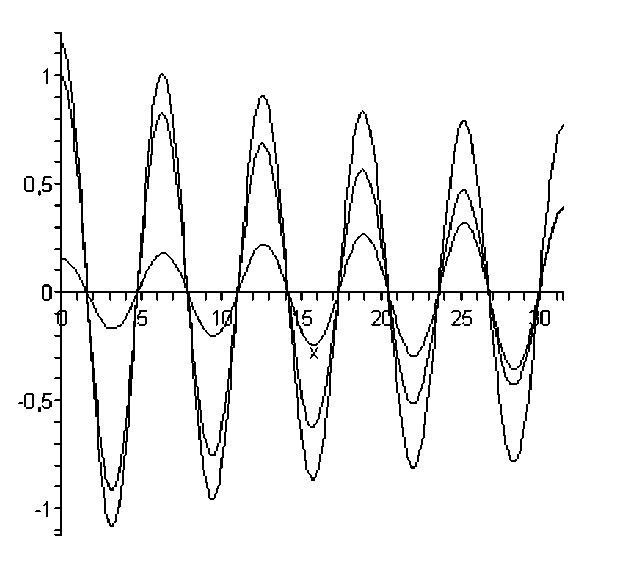
Рис. 1. Структура волнового поршневого поля на оси прямоугольного волнового стенда
Нераспространяющиеся волны могут также локализоваться и в окрестности отражающей стенки, что видно из формулы (5).
Заключение.
-
1. В работе показана возможность моделирования явления горизонтального турбулентного обмена для поля из падающих и отражённых поверхностных, длинных волн в прямоугольном стенде с произвольным соотношением сторон.
-
2. Показано, что волновое поле, состоящее практически только из бегущих волн, возникает в волновом стенде конечной длины благодаря влиянию диссипации энергии.
-
3. Получены новые условия отсутствия возбуждения поршневых, длинных волн горизонтальными гармоническими колебаниями щитового волнопродуктора.
Список литературы Длинные волны в прямоугольном стенде, вызванные пластиной
- Сретенский, Л. Н. Теория волновых движений жидкости/Л. Н. Сретенский. -Москва: Наука, 1977. -816 с.
- Вапняр, Д. У. Планетарные волны и течения в экваториальной зоне океана/Д. У. Вапняр. -Киев: Наукова думка, 1976. -222 с.
- Лепендина, Л. Ф. Акустика/Л. Ф. Лепендина. -Москва: Высшая школа, 1978. -448 с.
- Трепачёв, В. В. Дифракция гармонической волны на вертикальном щите в канале/В. В. Трепачёв//Колебания и волны в жидкости и газе. -Горький: Изд-во ГПИ, 1990. -С. 89-95.
- Трепачёв, В. В. Дифракция волн на пластине в узком канале/В. В. Трепачёв//Изв. вузов. Северо-Кавказ. региона. Естеств. науки. -2002. -№ 2. -С. 63-65.


