Доказательство необходимого признака существования тонкого слоя между двумя поверхностями

Одним из важных вопросов в теории смазки является вопрос формирования тонкого слоя между двумя поверхностями. Этот вопрос остается важным при решении задачи Капицы о качении шара по поверхности, при рассмотрении взаимодействия клина и иглы с деформируемой поверхностью. В приведенной работе формулируется и доказывается необходимые условия формирования тонкого слоя между двумя поверхностями.

2.    Постановка задачи и вывод необходимого условия для формирования тонкого слоя

Рассмотрим один из методов построения тонкого слоя между двумя поверхностями.

Пусть задана поверхность с уравнением

Г=Г^ХХ,Х2^.(1)

Это может быть сфера единичного радиуса с центром в точке О. Определим единичный вектор нормали к поверхности в точке А '

• -       12\

п л- , х(2)

и построим вектор, отложенный от центра сферы (рис. 1).

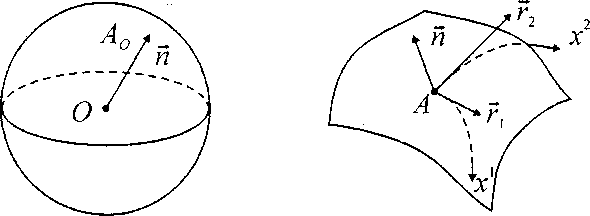
Рис. 1

Касательные плоскости, построенные в точке А поверхности и в точке Ио сферы, будут параллельными. Направляющими векторами для касательной плоскости поверхности в точке А будут базисные векторы

' дх* ’ а для сферической поверхности выбраны векторы тц ~ — дх’

Система векторов г, (z = 1, 2) компланарна системе векторов (z = 1, 2), то есть будут справедливы следующие линейные соотношения:

«,=2^4-(

4=1

Умножив равенство (5) на вектор rt скалярно, найдем 22

й, = ^m^rk r, = ^m^qk] .

4=1

Из равенства [1]

получим 2

-Ьи =^т^ку=т tJ.(8)

4=1

С учетом (8) приходим к формуле Вейнгартена

”,=~I№-(9)

л=1

Компоненты

Уч = пгп},(10)

являются компонентами метрического тензора сферы. Квадрат линейного элемента, то есть первая квадратичная форма сферы будет такой: 2 2

6 s0 =ИТ.^ У6 Х‘ 6 xJ •(

/=1 7=1

Коэффициенты (10) можем записать в виде 2 22

711=У.Т1^ь1,Чч=У.ь‘Ьч'< х=1 /=14=1

Для поверхности были введены два тензора с компонентами g₄ и b, _г Построим третий тензор с компонентами у_и, причем согласно (12), компоненты вновь построенного тензора являются сверткой тензора с компонентами Ь_у, при этом

Уч=Уц(13)

Таким образом, имеем

^-2/^ + ^=0,(14)

где Н, К- средняя и полная кривизна поверхности. Теперь возьмем вторую поверхность с уравнением

R-R^yVy(15)

Единичный вектор нормали второй поверхности обозначим

^ = Ду\у2у(16)

Базисные векторы поверхности равны:

А=^     (/ = 1,2).(17)

Эу,

При смещении по некоторой кривой из точки В в точку В 'вектор N имеет приращение 8 N (рис. 2), при этом касательная плоскость повернется на угол 8ф, равный

^ = ^|,(18)

отсюда следует, что квадрат 8ф ² равен

8ф7 =\б N^ =3 N-8 N.(19)

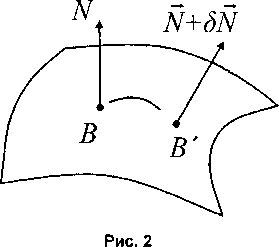
Вектор 5 N разложим по базисным векторам 7?,

SN^R^y1(20)

i=i

Базисные вектора R_t компланарны векторам N,

_2

N.^M^,(21)

А=1

так что разложение (20) можно заменить разложением такого вида:

2‘

SN^N^y.(22)

i=i

Третья квадратичная форма поверхности запишется

2 2

V^ZZW^/,(23)

1=1 2=г

Итак, каждая из рассматриваемых поверхностей имеет три квадратичные формы, причем для второй поверхности их можно записать в виде:

8S2=8R2, 8 l = "5 R-8 N, 8(p2=8N-8N.(24)

Первая квадратичная форма определяет квадрат расстояния между двумя выбранными точками В и В' по некоторой кривой поверхности; вторая - расстояние от точки В' до касательной плоскости в точке В; третья - квадрат угла поворота между касательными плоскостями в точках В и В'.

Вернемся к первой поверхности. Вектор 8 п может быть получен, если к вектору 8 г менить линейный оператор L

8 п = L8 г .

Линейный оператор (25) построим так, чтобы он переводил неколлинеарные векторы ^ в векторы у и й₂ соответственно

Z^ = й], L^ = й₂ .

Линейный оператор L оказывается самосопряженным, так как справедливо равенство Й ' ^2 ~ ^ " ^2 ~ ^2 ' ^Л = ^₂ ■ Й, .

Запишем теперь равенство

8 п ( 8 г )

8 S~ \8 S)

Производная по дуговой координате .S'

при-

(25) и г2

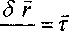
представляет собой касательный вектор к выбранной кривой единичной длины.

Обозначим ё_х и ё₂ - единичные векторы по главным направлениям линейного оператора L и запишем

---- = в] COS ф + ?2 sin ф ,

8 S где ф - угол между вектором ёх и вектором f .

С учетом разложения (4.30) равенство (4.28) запишем в таком виде:

^^ = L (ё, cos ф + e₂ sin ф^ = cos ф Ьё_х + sin ф Le₂.

Так как для главных значений линейного оператора справедливы равенства £(ё]) = Я]е1, Ь(е2) = Я2ё2, то производную от вектора п по дуговой координате 5 можем представить в виде 3 п           _       .    _

-—- = Л] cosip б] + Х2 sin ф е₂.

8 S

Обозначив кривизну нормального сечения поверхности К и учитывая, что

_ 8 г 8 п

найдем

К--^ cos² ф - ^ sin² ф .

Собственные значения линейного оператора L равны —Лц = К_х, — /Т = К₂,

а собственные векторы определяют главные направления поверхности. С учетом (4.36) получим формулы Эйлера

К = К_Х cos² ф - К₂ sin² ф.

Выпишем следующие производные:

8 г „   .„

---= cos ф е_х + sin ф е₂ ,

8 S

8 п           __

----= -к_х cos ф 6] - к₂ sin ф вэ .

8 8~

Умножив первую формулу (38) на к_х и складывая почленно со второй, найдем

8 п 8 г , х .„

8 д 8 » или

8 n + kx8 г = (к, -к2^5тф ё2 8 S.

Вектор 8 п + к_х 8 г коллинеарен вектору ё₂ . Аналогично векторы 8 п + к₂ 8 г и ё_х также коллинеарны. Так как выполняется условие ^ - е₂ = 0, то скалярное произведение векторов 8 и + к_х 8 г и 8 п + к₂ 8 г также будет равно нулю

( п + кх8 гу^8 п + к23 F) = 0.(40)

Равенство (40) преобразуем к виду

8 п-8 п + {кх+к2^8 п-8 п + кхк2 8 г-8 г =0.(41)

Так как выполняются равенства

8 ф"2" = 8 п-8 п , 8i = -^8n-8F,   8 S2 =3 г -8 г, то между тремя квадратичными формами существует связь

8 ф2-2^кх+к2^8 1 + кхк2 8 S2 = 0.(42)

Аналогичная связь имеется между коэффициентами трех форм (14).

Рассмотрим слой, образованный двумя поверхностями. Вторая поверхность получена из первой поверхности смещением точек поверхности по нормали на некоторую величину h = h(x', х2). Поэтому обе поверхности имеют общую параметризацию г = т^х1, х2); R = R^x\ x2j = r^x1, х2) +      х2).                   (43)

Произведем сферическое отображение поверхностей (рис. 3). Допустим, что для точек А и В поверхностей векторы оказались коллинеарными, причем скалярное произведение векторов n-N = 1. Третья квадратичная форма поверхности для сферы является первой квадратичной формой. При сферическом отображении точка А поверхности переходит в точку Ао на сфере (рис. 4). Касательная плоскость поверхности переходит в касательную плоскость сферы, поэтому пх х Я2 = a rj х r2, NxxN2 = р RxxR2.                          (44)

У множив векторно обе части равенств (44) на ^ х F₂ и R_x х R₂ соответственно, получим

V»¹ ЙЛ     Л‘Л  'УС

Ц, ■ Й] г2 • й2         г2 ■ Г, г2 ■ г2

R\-N\ R_VN₂ R_VR_X R_XA R₂-N_x r₂-n₂^p R₂-R_x r₂r₂

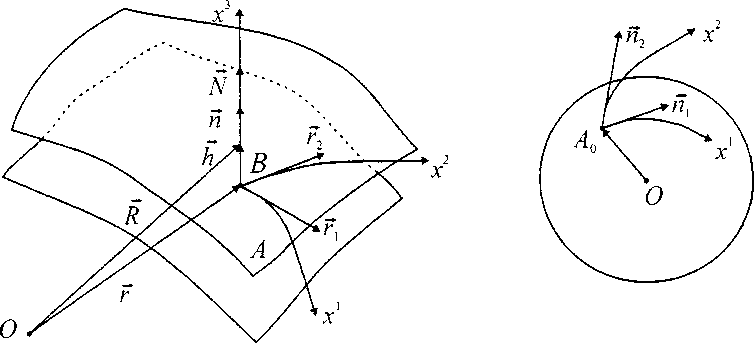
Рис. 3

Рис. 4

Скалярные произведения, входящие в равенства (45), являются коэффициентами квадратичных форм

^И ^2      511 512

= а

-6_2]   -b₂₂      g_2x g₂₂

^11    ^12 _ р 511

"^21   ~^Т1       ®1

Из равенств (46) определим коэффициенты а и р

b_xxb₂₂ Ь_Х2 , 511522-512

^11^22 ^12

511522 -512

Обозначим а = К, Р = К и равенства (48) запишем в виде пх х й2 = К гх х r2, Nx х N2 = К Rx х R2 .                            (48)

Если а и р отличны от нуля, то векторы п_х и и₂. а также N_x и N₂ не коллинеарны.

Рассмотрим случай, когда и = N . В этом случае

К г_х х г₂ = К R_x х R₂ .

Умножим равенство (49) скалярно на вектор п

К {fxxr2yii- К ^RxxR2y N .

Так как векторы г, r₂ п , а также R_x R_T N образуют правые тройки, то объемы, построенные на этих векторах, равны по величине площадям, построенным на базисных векторах. Поэтому отношение гауссовых кривизн должно быть положительным

£

К

>0.

Если же n = -N, то отношение гауссовых кривизн двух поверхностей будет отрицательным.

В первом случае условие (51) является необходимым для формирования тонкого слоя между двумя поверхностями. Таким образом доказано утверждение для формирования тонкого слоя (признак впервые сформулировал Геннадий Алексеевич Завьялов).

3. Необходимый признак формирования тонкого слоя между двумя поверхностями

Если точка А и нормальным вектором п принадлежит эллиптической поверхности, то такой же должна быть вторая поверхность с принадлежащей точкой В и нормалью N -п . Если же первая поверхность с точкой А и нормальным вектором п эллиптическая, а другая поверхность с точкой В и нормалью N = -й гиперболическая, то отношение гауссовых кривизн поверхностей будет отрицательным и условие формирования слоя не будет выполняться.