Доказательство теоремы о среднем значении с использованием пакета MathCAD

ПОСТАНОВКА ЗАДАЧИ

Известно, что обобщенная теорема о среднем значении (Коши) [1, с. 334] имеет следующую формулировку:

производные У (f) и ф (() двух функций / (t) и фУ), дифференцируемых в замкнутом промежутке (а, Ь), не обращаются одновременно в нуль нигде внутри этого промежутка.

Пусть при этом одна из функций Д (t) , фУ) имеет неравные значения на концах интервала [например, фУГ) Ф ф(Ь)]. Тогда приращения Д(5) - У У1) и фУУ-фУУ данных функций относятся как их производные в некоторой точке t = Т , лежащие внутри промежутка (а, Ь), т.е.:

f(b)-f(a)   /(г)^(Ь)-^(а) ф^

1 Авторы - доценты кафедры технологии металлов

РЕШЕНИЕ

Возьмем пример из литературных источников[1, с. 335]. Рассмотрим функции f(t) = t³ и фУ) = t² в промежутке от 0 до 2. На конце t = 0 производные У (t) =3t² и ф У) =2t обращаются в нуль, но внутри промежутка обе отличаются от нуля. При этом каждая из функций УУУ ф(0 имеет неравные значения на концах t = О и t = 2. Условия теоремы Коши выполнены. Значит отношение

f(b)-f(a) _ Л2)-/(0) = 23^2 р(Ь) - ф(а) фУ1) - ф(0) У должно равняться отношению

/ л-Л2 _з,

Ф У) It 2

в некоторой точке \ = У лежащей между а = 0 и b = 2.

Действительно, с равнение — t = 2 имеет корень t ~ "            2

— , лежащий внутри промежутка (0. 2).

Рассмотрим решение вышеприведенного примера [:] на компьютере в системе MathCAD с использованием решающих блоков [2].

Зададим границы интервала nl = 0.001 - значение левой границы интервала;

nl = 2 - значение правой границы интервала.

х - переменная;

х:= п1,0.2..п2 - ранжированная переменная с шагом 0.2;

fl (х) := х3 - первая функция;

f2(x) := х" - вторая функция;

/Я(а) :=-----Д1(а) - первая производ- d(x)

ная первой функции;

рУх) :=----У Ух) - первая производ- d(x)

ная второй функции.

Построим графики функций и их производных (см. рис. 1):

и ремонта

Труды лесоинженерного факультета ПетрГУ

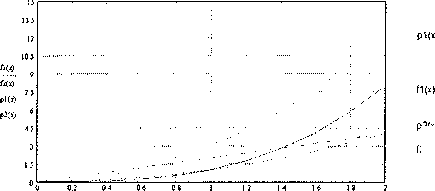
р2(х)

ОД

Рис. 1. Графики функций первой и второй производной

Зададим пошаговые значения функций и их производных:

X	П(х)	р1(х)	(2(х)	р2(х)
0.001	10'9	3*10"6	НГ&	2*10"30'4
0.2	0.008	0.12	" 0.04	0.4
0.399	0.064	0.478	. 0.159	0.798
0.598	0.214	1.073	0.358	1.196
0.797	0.506	1.906	0.635	1.594
0.996	0.988	2.976	0.992	1.992
1.195	1.706	4.284	1.428	2.39
1.394	2.709	5.83	1.943	2.788
1.593	4.042	7.613	2.538	3.186
1.792	5.755	9.634	3.211	3.584
1.991	7.892	11.892	3.964	3.982

Запишем ключевое слово решающего блока:

Given.

Запишем условие (1):

fl(n2) - fl(nl) _/?1(х) /2(п1) -/2(п1) " рХхУ

Найдем значение переменной х:

Find(x) = 1.333

Или 1.333 = — , что соответствует решению приме ра [1].

ВЫВОДЫ

Как видно из приведенного выше доказательства теоремы о среднем значении (Коши), в пакете прикладных программ MathCAD для инженерных расчетов благодаря простоте и удобству все более широкое применение находят численные методы расчета, реализованные в программном обеспечении.