Долгоживущие перепутанные состояния в двойной модели Джейнса – Каммингса с прямым диполь-дипольным взаимодействием кубитов

Квантовые перепутанные состояния имеют фундаментальное значение в квантовой физике как для понимания нелокальности квантовой механики, так и для практических применений в квантовых вычислениях и коммуникациях [1]. В связи с этим в последние годы предприняты большие усилия по исследованию свойств перепутанных состояний, механизмов их генерации и контроля в различных системах. Хорошо известно, что модель Джейнса – Каммингса (МДК) является простейшей физической моделью, описывающей взаимодействие естественного или искусственного двухуровневого атома (кубита) с полем одномодового резонатора [2]. Указанная модель была использована для описания широкого спектра явлений в квантовой оптике и конденсированных системах, таких как захваченные ионы, квантовые точки,

сверхпроводящие цепи др. [3]. Для изучения более широкого круга явлений, обусловленных взаимодействием систем кубитов с квантовыми полями резонаторов, в последние годы были исследованы многочисленные обобщения МДК. Так, в работе [4] была предложена так называемая двойная модель Джейнса – Каммингса (ДМДК), состоящая из двух двухуровневых атомов (кубитов) и двух мод двух индивидуальных резонаторов, при условии, что каждый атом взаимодействует только с полем одного резонатора. Исследовав динамику парного перепутывания кубитов в этой модели, авторы обнаружили, что для малофотонных полей перепутывание кубитов не является стационарным и в системе могут проявляться периодические флуктуации в виде мгновенной смерти перепутывания (МСП). В последнее время появилось большое число работ, посвященных изучению перепутывания кубитов в рамках модели ДМДК и ее обобщений.

[^^■1 © Башкиров Е.К., 2025

В работе [5] изучено влияние динамического сдвига Штарка на перепутывание кубитов в рамках ДМДК и показано, что при больших значениях параметра штарковского сдвига два кубита могут оставаться в стационарном перепутанном состоянии. В работе [6] была рассмотрена ДМДК при наличии расстройки частот переходов в кубитах и полей резонаторов в случае различных значений констант связи кубитов с полями резонаторов и показано, что долгоживущие перепутанные состояния кубитов могут быть получены, когда один кубит нерезонансно взаимодействует с полем резонатора, а другой ‒ полностью отстроен от частоты своего резонаторного поля. В работе [7] обсуждалось влияние различных начальных состояний кубитов на их перепутывание в процессе эволюции. Исследование динамики перепутывания кубитов в двухфотонной ДМДК в случае, когда поля резонаторов предварительно максимально перепутаны, проведено в работе [8]. Авторы также показали, что наличие когерентности начальных состояний кубитов уменьшает степень их перепутывания в процессе эволюции и приводит к возникновению МСП. Рассмотрение ДМДК с керровской средой показало, что с помощью керровской нелинейности можно контролировать динамику перепутывания и подавлять явление МСП [9–11]. Немарковская релаксация в рамках ДМДК рассматривалась в [12]. Динамика перепутывания кубитов в рамках ДМДК вне приближения вращающейся волны изучалась в [13]. Авторы показали, что исчезновение перепутывания кубитов может быть индуцировано противовращательными членами. Перепутывание кубитов в рамках ДМДК с тепловыми полями резонаторов исследовалось в работах [14; 15]. Динамика перепутывания двух идентичных кубитов в рамках двухфотонной ДМДК с учетом расстройки между частотами переходов в кубитах и двойной частотой мод поля резонаторов, а также керровской среды в обоих резонаторах анализировалась в работе [16].

Исследованию динамики перепутывания различных подсистем, таких как кубит – кубит, кубит – поле и поле – поле для ДМДК с полями резонаторов в сжатых когерентных тепловых состояниях посвящена недавняя работа [17].

Для сверхпроводящих колец с джозефсонов-скими переходами удалось экспериментально реализовать условия, при которых прямое ди-поль-дипольное взаимодействие кубитов может существенно превосходить константу кубит-по- левого взаимодейвия [18; 19]. В этой связи в нашей работе [20] исследовалось влияние прямого диполь-дипольного взаимодействия кубитов на их перепутывание в рамках нерезонансной ДМДК [20]. При этом была рассмотрена модель с одинаковыми константами взаимодействия кубитов с полями индивидуальных резонаторов и одинаковыми расстройками частот кубитов и полей резонаторов. Однако за счет флуктуаций положения кубитов в полях стоячих волн индивидуальных резонаторов практически невозможно добиться равенства констант кубит-полевого взаимодействия. Для макроскопических объектов – сверхпроводящих колец – невозможно также добиться равенства расстроек. Поэтому представляет существенный интерес обобщить результаты работы [20] на случай неидентичных кубитов.

В данной работе мы рассматриваем динамику нерезонансный ДМДК с учетом прямого диполь-дипольного взаимодействия между неидентичными кубитами. В качестве начальных состояний полей резонаторов выбраны вакуумные состояния, а в качестве начальных состояний кубитов ‒ перепутанные состояния белловского типа. С использованием критерия перепутывания кубитов – отрицательности, мы исследовали зависимость степени перепутывания от начальных состояний кубитов и параметров рассматриваемой модели, таких как соотношение констант кубит-полевого взаимодействия, интенсивности дипольного взаимодействия и расстроек между частотами перехода в кубитах и частотами полей резонаторов.

1.    Модель и ее точное решение

Мы рассматриваем два неидентичных сверхпроводящих кубита Q ₁ и Q ₂ с частотами энергетических щелей ω ₀₁ и ω ₀₂ соответственно, взаимодействующих нерезонансно каждый со своим индивидальным резонатором, которые мы будет обозначать как « a » и « b » (кубит Q ₁ взаимодействует с модой резонатора « a », а кубит Q ₂ с модой « b »). Из-за возможности случайных отклонений в положении кубитов относительно пучностей стоячих волн в резонаторах будем полагать, что константы связи между кубитами и полями резонаторов не равны. Учтем также прямое диполь-дипольное взаимодействие кубитов. Тогда в системе отсчета, вращающейся с частотой моды резонаторов, гамильтониан этой системы можно записать в виде

H = (1/2) й (5..о z + 5₉g z ) + h Y_n ( o + a + a ⁺ o - ) + (1) 11 22 a 1 1

+ Yb(^+b + b+^2) + bJ(°+c2 + ®-®+ ), где (1 / 2)стZ - оператор инверсии населенности в i-м кубите (i = 1,2); ст + = | +> ii (-1, ст - =| -> ii (+ | -операторы переходов между возбужденным | +>i и основным | ->i состояниями в i-м кубите; а+ и а - операторы рождения и уничтожения фотонов в резонаторной моде «a»; b+ и b - операторы рождения и уничтожения фотонов в резонаторной моде «b»; у a - константа связи кубита Q1 с резонаторной модой «a»; уb - константа связи кубита Q2 с резонаторной модой «b»; 5a = ГО01 - го и 5b = = ©02 -го - расстройки частот кубитов Qi и Q2 и мод полей «a» и «b» соответственно и J - константа прямого диполь-дипольного взаимодействия кубитов.

Выберем в качестве начальных состояний кубитов перепутанные состояния белловского типа:

• ¹    ^ ⁽⁰⁾ ^ QQ = ^cos ^ ^{1 +} , ^-^^{+ sin} ^ ^{1 -} , ⁺> ^{,                  (2)}

и

• ¹    ^ ⁽⁰⁾ ^ QQ₂ = ^cos ^ ^{1 +} , ⁺^^{+ sin} ^ ^{1 -} , ^-> ^{, (3)} где 0 < 0 < п . Для полей резонаторов выберем вакуумные начальные состояния так, что полевая волновая функция двух мод имеет вид

| W) > F = |0 > а ® |0 > _b = |0,0 ) .

Эволюция рассматриваемой системы для начальных состояний кубитов (2) происходит в четырехмерном гильбертовом пространстве с базисными векторами

| ^- , ^{- ,0,1} > , | ^- , ^{- ,1,0} > , | ^- , ^{+ ,0,0} > , | ⁺ , ^{- ,0,0} > .

Для нахождения временной волновой функции воспользуемся представлением «одетых» состояний, т. е. собственных функций гамильтониана (1). В общем случае «одетые» состояния имеют чрезвычайно громоздкий вид. Поэтому «одетые» состояния для произвольных соотношений между параметрами модели в настоящей работе не приводятся. Ниже показаны явные выражения для «одетых» состояний в двух специальных случаях.

1. Пусть 5 a = 5 b =0 и у a ^ у b . В этом случае собственные функции гамильтониана (1) могут быть записаны как

I Ф i > = ^ i ( X i 1 1 - , - ,0,1 > + X i 2 l - , - ,1,0 >+ (4) ⁺ X i 3 | ^- , ^{+ ,0,0} >⁺ X i 4 | ⁺ , ^{- ,0,0} > )

(i = 1,2,3,4), где

^ i =1/ ^I X i 1 1² + 1 X i 2 1² + 1 X i 3 1² + 1 X i 4 I²

и

X 11 =

2 g a

- 1 + g ² -a ² + B’

X 12 = X 22 = I ---------------,

1 + g ² +a ² - B

^X 13 =

-

2a a 1 + g + a - B - 1 + g ² - a ² + B

X 14 = X 24 = X 34 = X 44 = 1,

X 31 = X 41 =

2 g a

1 - g ² +a ² + B ’

X32    X42     I--------------, у 1 + g + a + B

^X 33 =

X 43 =

2a a ^ 1 + g + a + A 1 - g ² +a ² + B

Здесь

A = 5 / y, a = J / y, g = yb / Ya и B = ^(g2 -1)2 + 2(g2 + 1)a2 +a4.

Соответствующие собственные значения энер гии есть

E 1 = ^-Y a

^ 1 + g ² +a ² - B

_E      'J ^{1 + g 2 +a} 2 ^{- B}

• ^{2    Y} a          2           ^,

• 2.    Пусть 5 a = 5 ь = 5 и y a = Y b = Y . В рассматриваемом случае собственные функции гамильтониана (1) также могут быть представлены в виде (4) с коэффициентами

  X 11 =

  

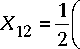
  - a - 4 + ( a - A )

  
  

1 + g ² + a² + B

^E 3 = -Y a         ,--------

E 4 = Y a

•J 1 + g ² + a² + B

+ A

X 13 =1, X 14 = 1;

X 21 = X 22 = ^^-a + 4' 4 + ( a - A)² + A

X 23 = 1, X 24 = 1;

X 31 = ~f -a - A + ^ 4 + ( a + A ) ^ ,

X 32 = ~ f a + A - V 4 + ( a + A)² ^ ,

• ^X 33 = ^{- 1}, ^X 34 = ^1;

• X 41 = ~ f -a - A - V 4 + ( a + A ) ^ ,

X 42 = — ^ a + A + ^ 4 + ( a + A )

X 43 = - 1, X 44 =1.

Соответствующие собственные значения энергии есть

E 1 = -^Y 2

El = Y ¹

- 2 aA + A 2 I ,

- 2 aA + A ²

E o = -у ¹ 1 -a + A - V 4 + a ² + 2 aA +A ²

E 4 = у—| — a + A + у/ 4 + a + 2 aA + A

Временная волновая функция рассматриваемой модели может быть найдена с использованием оператора эволюции следующим образом:

| У ( t ) ) = e - ^iHt / ^h | W)) .

Для того чтобы найти явный вид временной волновой функции | У ( t ) ) для начального состояния кубитов (2) и вакуумного состояния поля резонатора, достаточно начальную волновую функцию | У (0) ) представить в виде комбинации собственных функций (4). В результате временная волновая функция системы примет вид

I ^ ( t ^{) )} = ^С 1 ⁽ t ) | ^- , ^{- ,0,1 )} + С 2 ⁽ t ) | ^- , ^{- ,1,0 )} +                ⁽5)

+ ^С 3 ⁽ t ) ^{| -} , ^{+ ,0,0 )} + ^С 4 ⁽ t ) ^{| +} , ⁺ , n ⁾ .

Мы нашли явный вид коэффициентов C_i ( t ) ( i = 1,2,3,4) для обоих специальных случаев и выбранного начального состояния кубитов. Однако из-за чрезмерно громоздкого вида указанные выражения в настоящей работе опущены.

Для начального состояния кубитов (3) эволюция вектора состояния происходит в 5-мерном гильбертовом пространстве с базисом

• ^{1    +} , ^{+ ,0,0 )} , ^{1 +} , ^{- ,0,1 )} , ^{1 -} , ^{+ ,1,0 )} ,

• ^{1    -} , ^{- ,1,1 )} , ^{1 -} , ^{- ,0,0 )} .

• 2.    Вычисление отрицательности

Временная волновая функция системы в этом случае имеет вид

| У ( t ) ) = ф t ) I + , + ,0,0 ) + С 2 ¹ ) ( t ) I + , - ,0,1 ) +            (6)

+ ^с 31 ⁾⁽ t )¹ - , ^{+ ,1,0 )}+ ^с 41 ⁾⁽ t )¹ - , ^{- ,1,1 )}+ ^с 51 ⁾⁽ t )¹ - , ^{- ,0,0 )} .

«Одетые» состояния и коэффициенты С р)( t ) ( i = 1,2,3,4,5) даже для рассмотренных выше специальных случаев для начальных состояний (2) имеют слишком громоздкий вид, чтобы представить их в настоящей работе.

В настоящей работе нами в качестве количественного критерия перепутывания кубитов выбран параметр Переса - Хородецких, или отрицательность. Отрицательность определяется стандартным образом в виде следующего выражения:

s = - 2 ^ - , где ц ^- - отрицательные собственные значения частично транспонированной по переменным одного кубита двухкубитной матрицы плотности.

Используя явные выражения для временных волновых функций системы (5) и (6), нетрудно получить матрицу плотности изучаемой системы в виде

р ( t )=| У ( t ЖС t )|.                                   (7)

Усредняя полную матрицу плотности (7) по переменным поля, можно получить матрицу плотности подсистемы кубитов

Р Q 1 Q ₂( t ) = T Field^ t Ж( t )|.                      (8)

В двухкубитном базисе | + , +) , | + , -) , | - , +) , | - , -) матрица плотности подсистемы кубитов в случае их начального состояния (2) принимает вид

	f 0	0	0	0 '
	0	V ( t )	H ( t )	0
Р QQ 2 ( t ) =	0	* H ( t )	W ( t )	0	.                             (9)
	0 <	0	0	R ( t ) }

Матричные элементы (9) есть

V ( t )=| C ₄( t )|², W ( t )=| C ₃( t )|²,

R ( t ) =| С 1 ( t ) |² + | С 2 ( t ) |², H ( t ) = С 4 ( t ) С 3 ( t Л

Частично транспонированная по переменным одного кубита по отношению к (9) двухкубитная матрица плотности есть

	f 0	0	0	H ( t )
Р nn ( t ) =	0	V ( t )	0	0	.                   (10)
Q 1 Q 2	0	0	W ( t )	0
	ч H ( t )	0	0	R ( t ) ?

Матрица (10) имеет всего одно собственное значение, которое может быть отрицательным. В результате отрицательность для рассматриваемого начального состояния кубитов может быть представлена в виде

s ( t} = /u ( t ) - R ( t ))² + 4| H ( t )|² - U ( t ) - R ( t ). (11)

а                                                   б

в                                                                   г

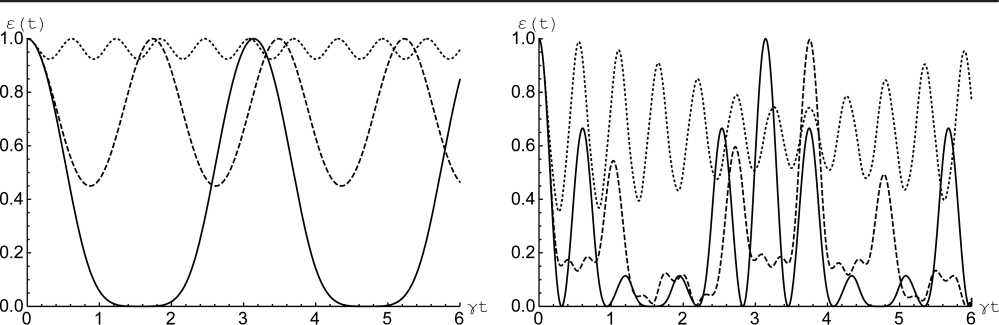
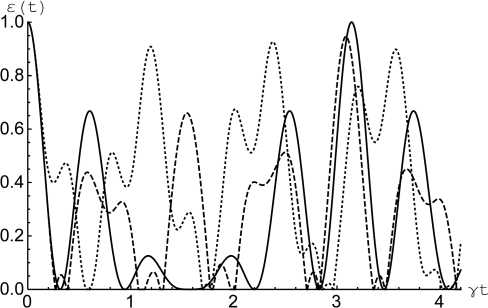
Рис. 1. Отрицательность как функция безразмерного времени у t ( у = у a ) для начального состояния кубитов (2) при 0 = п /4 и ⁶ a = ⁵ b = 0, Y b = Y _a ( а ); ⁵ a = ⁵ b = 0, Y b = 5 Y a ( б ), ⁵ b = ⁵ a = 10, Y b = Y a ( в ) и 5 b = 8 _a = 10, у b = 5 y a ( г ). Безразмерная константа диполь-дипольного взаимодействия а = 0 (сплошная линия), а = 3 (штриховая линия) и а = 10 (точечная линия)

Fig. 1. Negativity vs scaled time y t ( у = у _a ) for initial qubits state (2) with 0 = п /4 and 5 a = 5 b =0, y _b = y a ( a ); 5 a = 5 b = 0, y ь =5 y a ( b ), 5 b = 5 _a = 10, Y ь = Y _a ( c ) and 5 b = 5 a = 10, у ь = 5 у a ( d ). Scaled dipole-dipole coupling а = 0 (solid), а = 3 (dashed) and а = 10 (dotted)

Для начального состояния кубитов (3) редуцированная двухкубитная матрица плотности имеет вид

P Q 1 Q 2 ( t ) =	' U 1 (t ) 0 0 4 H 1 ( t ) *	0 V 1( t ) H 2( t) 0	0 H 2( t ) W 1( t ) 0	H 1 ( t ) ^ 0 0 R 1 ( t ) ;	,            (12)
где
U 1( t )=| C 1(1)( t )|2,		H 1( t )=	C 1 (1) ( t ) C 5 (1)*	( t ),
H 2( t )= C 2(1)( t ) C 3 (1)*		( t ),
V 1 ( t )=| с 21) ( t ) |2,		W 1 ( t )=|	с 31) ( t )|2,

R 1 ( t )=| С 41) ( t ) |² + 1 с 5 ¹⁾( t ) |² .

Соответствующая (12) частично транспонированная по переменным одного кубита матрица есть

	' U 1 ( t )	0	0	H 2( t )
Poo ( t ) =	0	V 1( t )	H 1 ( t )	0     .            (13)
Q 1 Q 2	0	H 1( t )	W 1( t )	0
	, H 2( t )	0	0	R 1 ( t ) ?

Матрица (13) имеет два собственных значения, которые могут принимать отрицательные значения. В результате для начального состояния (3) отрицательность принимает вид

£ ( t ) = 7( U 1 ( t ) - R 1 ( t ))² + 4| H ₂( t ) |² - U 1 (t ) - R 1 ( t ) + (14) + 7 ( V 1 (t ) - W 1 ( t ))² + 4| H 1 ( t ) |² - V 1 ( t ) - W 1 ( t ).

Результаты численных расчетов временной зависимости отрицательностей (11) и (14) для различных значений параметров модели представлены на рис. 1–2.

3.    Результаты и обсуждения

Результаты расчетов временной зависимости отрицательности для начального состояния кубитов (2) приведены на рис. 1, а для начального состояния кубитов (3) - на рис. 2. Значениям безразмерной константы диполь-дипольного взаимодействия кубитов соответствуют кривые: а = 0 (сплошные линии), а = 3 (штриховые линии)

б

в

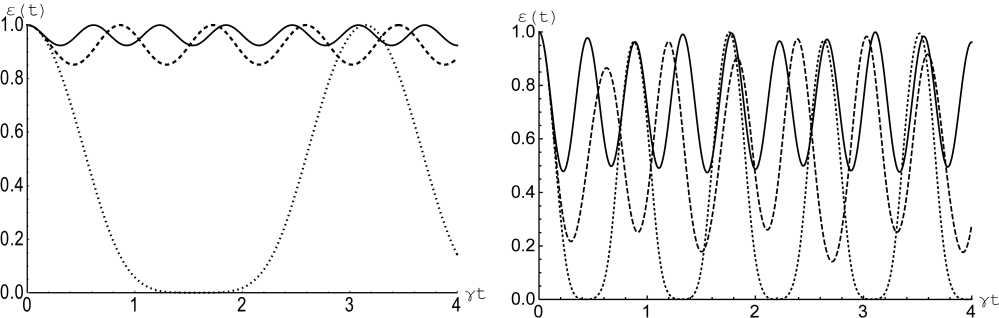
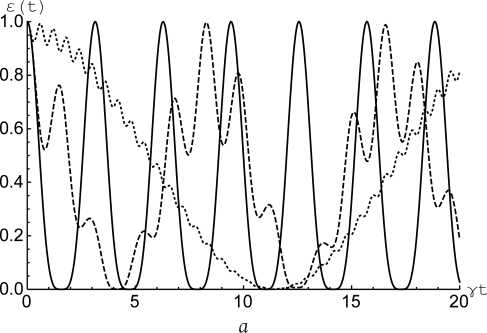
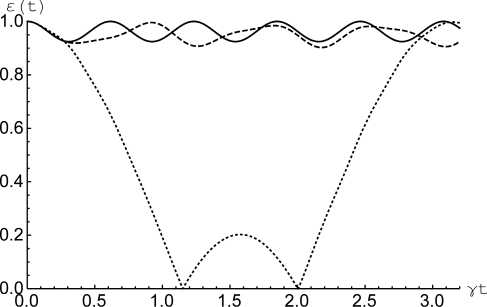
Рис. 2. Отрицательность как функция безразмерного времени

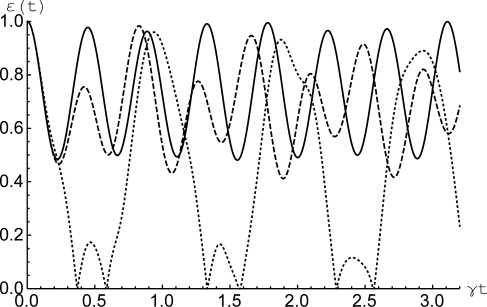
г

γ t ( γ≡γ _a ) для начального состояния кубитов (3) при θ = π /4 и

⁶ a = ⁶ b = 0, Y b = Y _a ( а ); ⁶ a = ⁶ b = 0, Y b = 5 y a ( б), ⁵ b = ⁵ a = 10, Y b = Y a ( в ) и ⁵ b = ⁵ _a = 10, Y b = 5 y a ( г ). Безразмерная константа диполь-дипольного взаимодействия α =0 (сплошная линия), α =3 (штриховая линия) и α = 10 (точечная линия)

Fig. 2. Negativity vs scaled time y t ( Y-Y a ) for initial qubits state (3) with 0 = n /4 and 5 a = 6 b =0, y b = Y _a ( a ); 6 a = 6 b =0, y b =5 Y _a ( b ), ⁶ b = ⁶ a = ^10, Y b = Y a ^{( c} ) ^{and 5} b = ⁶ a = ^10, γ _b =5 γ _a ( d ). Scaled dipole-dipole coupling α =0 (solid), α =3 (dashed) and α =10 (dotted)

и a = 10 (точечные линии). На рис. 1, а и б представлена отрицательность как функция безразмерного времени γt для модели с резонансым взаимодействием кубитов и поля в случае начального состояния кубитов вида (2). Из рис. 1, а видно, что для случая, когда константы взаимодействия кубитов с полем резонатора одинаковы, включение диполь-дипольного взаимодействия приводит к существенному уменьшению амплитуд осцилляций Раби отрицательности и, соответственно, к стабилизации начального перепутывания кубитов. На рис. 1, б представлены аналогичные зависимости для модели с различными константами кубит-фотонного взаимодействия. Из рисунка видно, что в рассматриваемом случае влияние диполь-дипольного взаимодействия на степень перепутывания кубитов намного уменьшается, так что существенной стабилизации начального перепутывания кубитов удается достичь лишь при значительно больших интенсивностях прямого взаимодействия кубитов. На рис. 1, в и г представлена отрицательность как функция безразмерного времени γt для нерезонансного взаимодействия кубитов и поля и начального состояния кубитов (2). Рис. 1, в соответствует одинаковым константам кубит-фотонного взаимодейвия, а рис. 1, г - различным. Из рисунков хорошо видно, что включение прямого диполь-дипольного взаимодействия кубитов для случая нерезонансного взаимодействия кубитов и поля приводит к обратному эффекту, т. е. к увеличению амплитуд осцилляций отрицательности и, соответственно, к невозможности реализовать в системе долгоживущие стабильные перепутанные состояния кубитов.

На рис. 2, а и г представлена отрицательность как функция безразмерного времени yt для модели с резонансым взаимодействием кубитов и поля и начального состояния кубитов (3). Для кубитов с одинаковыми константами кубит-полевой связи (рис. 2, а) включение диполь-дипольного взаимодействия приводит к увеличению периода осцилляций отрицательности, но не влияет на максимальную степень перепутывания кубитов, возникающую в процессе их эволюции. Для куби- тов с разными константами кубит-полевой связи (рис. 2, б) ситуация принципиально иная. Включение прямого взаимодействия кубитов увеличивает максимальную степень их перепутывания в процессе эволюции. На рис. 2, в и г представлена отрицательность как функция безразмерного времени γt для модели с нерезонансным взаимодействием кубитов и поля и начального состояния кубитов (3). В рассматриваемом случае влияние прямого диполь-дипольного взаимодействия кубитов на степень их перепутывания аналогично влиянию указанного параметра для начального состояния кубитов вида (3).

Заключение

В данной работе в рамках двойной модели Джейнса – Каммингса рассмотрена динамика перепутывания двух дипольно связанных сверхпроводящих кубитов с различными значениями констант кубит-фотонной связи и расстроек частот переходов в кубитах и частот резонаторных полей. В качестве критерия степени перепутывания кубитов выбрана отрицательность, а в качестве начальных состояний кубитов ‒ максимально перепутанные двухкубитные состояния. Началь- ные состояния полей резонаторов ‒ вакуумные поля. Исследована зависимость максимальной степени перепутывания кубитов от интенсивности диполь-дипольного взаимодействия, а также расстроек и соотношения констант кубит-фотон-ных связей. Результаты расчетов выявили, что эти параметры оказывают существенное влияние на периоды и амплитуды осцилляций Раби отрицательности. Показано, что начальные состояния кубитов вида (2) в случае резонансного взаимодействия кубитов с полями резонаторов могут рассматриваться при наличии интенсивного диполь-дипольного взаимодействия в качестве долгоживущих стабильных перепутанных состояний для любых соотношений констант кубит-фотонной связи. В нерезонансном случае такие состояния могут быть реализованы только для системы с одинаковыми константами кубит-полевого взаимодействия. При этом начальные состояния кубитов вида (3) при наличии интенсивного диполь-дипольного взаимодействия могут быть долгоживущими стабильными состояниями только в случае резонансного взаимодействия кубитов с полями резонаторов и одинаковыми константами кубит-фотонного взаимодействия.