Допустимые планы в транспортной задаче

Рассмотрим вопрос о числе решений (планов) транспортной задачи (ТЗ) вне зависимости от векторов мощностей и емкостей участников перевозок. Это означает, что транспортная таблица рассматривается без указания числовых характеристик, описывающих наличие груза у поставщиков и потребностей потребителей. Здесь нас не интересует поиск экстремума целевой функции, поэтому различные формы тарифов и связанные с этим ограничения также выпадают из круга нашего внимания.

Такая задача интересна сама по себе [1], а также для оценки числа возможных решений для модифицированных ТЗ с неединственным решением, когда нужно оценить число возможных локальных экстремумов [2-4]. Различные модификации ТЗ с усложненной постановкой находят широкое практическое применение [5-7], поэтому дополнительная информация о свойствах множеств их решений может оказаться весьма полезной.

По сути нас интересуют способы заполнения транспортной таблицы для широкого класса реальных ТЗ. Внешними параметрами остаются только число поставщиков и потребителей. Внутренние ограничения связаны с постановкой ТЗ: в заполненной транспортной таблице не должно быть пустых строк и столбцов. Будем рассматривать число таких базисных решений и называть их допустимыми.

В задачах линейного программирования базисными называют переменные, каждая из которых входит в единственное ограничение задачи с еди -ничным коэффициентом [8]. Применительно к ТЗ это условие означает, что число заполненных клеток в транспортной таблице должно быть ровно на единицу меньше общего числа участников перевозок, при этом в решении не должно быть циклов, построенных на заполненных клетках [8].

Фактически задача становится комбинаторной, нужно найти число способов заполнения ячеек прямоугольной таблицы (например, звездочками) с учетом отмеченных выше требований. Тогда для каждого варианта заполнения найдется бесконечное число ТЗ, для которых данный вариант будет одним из базисных решений. Если же говорить о подсчете числа базисных решений для конкретной ТЗ, то оно заполнит часть из найденного множества.

Материалы и методы

Начнем с простейшего случая ТЗ размерности 2х2. Число заполненных клеток должно быть равно трем, поэтому одна клетка остается свободной . Этой клеткой может оказаться любая из имеющихся четырех, поэтому число возможных решений N2=4.

Рассмотрим случай таблицы 2х3. Нетрудно убедиться, что число допустимых планов равно 12. Если заполненная клетка одна в строке или столбце, то она насыщена. Обозначим единственную заполненную клетку в строке минусом, а в столбце плюсом. Ненасыщенные клетки обозначим звездочками. Тогда получим следующий набор таблиц с допустимыми планами, которые назовем трафаретами (рис. 1).

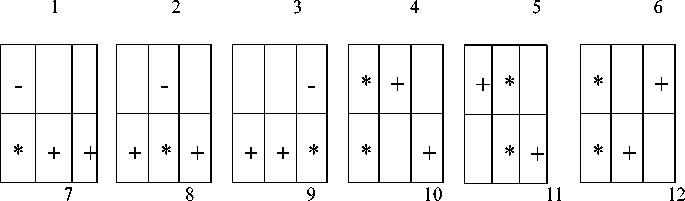
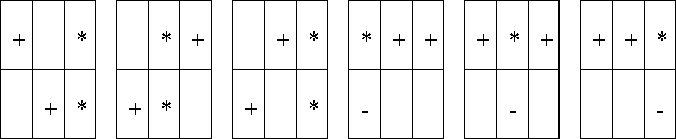
Рис. 1. Допустимые планы для ТЗ размерности 2х3

Рассмотрим ТЗ такого же размера и для каждой ячейки укажем насыщающую поставку, а в соседней таблице расставим знаки насыщений (рис. 2).

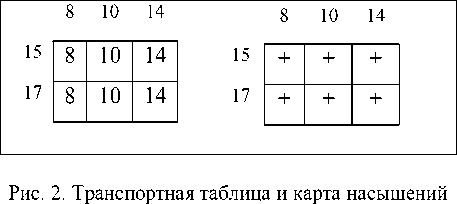
Накладывая последнюю таблицу на представленные выше трафареты, заметим, что совпадение знаков наблюдается с шестью трафаретами под номерами 4–9. Заполняя эти трафареты, получим все 6 базисных планов данной ТЗ (рис. 3).

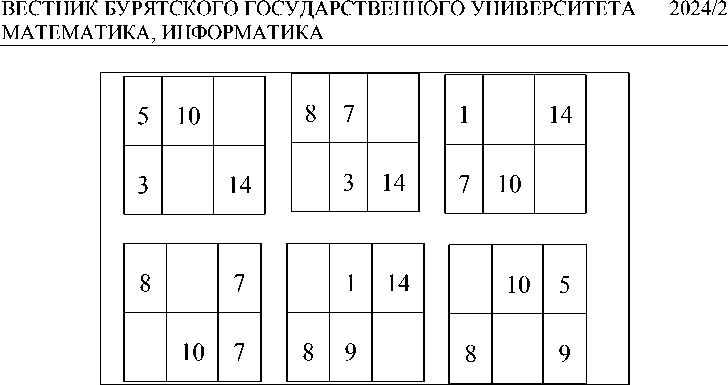
Рис. 3. Базисные планы конкретной ТЗ

Этот пример показывает, что допустимые планы могут оказаться полезными при подсчете числа базисных планов конкретной ТЗ. Для ТЗ размера 3х3 рассмотрим одну из строк, например, первую. Пусть в ней заполнены 3 клетки, тогда в двух других будет заполнено по одной. Вариант такого заполнения приведен в таблице 1.

Таблица 1

*	*	*
*
	*

Очевидно, заполнить можно любую ячейку во второй и третьей строках, а полностью заполненной может быть не только первая, но и любая другая строка. С учетом этого число решений такого вида равно 3х3х3=27.

Пусть теперь в первых двух строках заполнены по две ячейки, а в третьей одна (табл. 2). Во второй строке обязательно должна быть заполнена третья ячейка, чтобы не образовался цикл. Тогда первую строку можно заполнить тремя способами, вторую двумя, а третью тремя. С учетом того, что строчка с одной заполненной клеткой может быть на любой из трех позиций, получаем число решений такого вида: 3х2х3х3=54. Других вариантов нет, поэтому N3=27+54=81.

*	*
*		*
*

Для задачи размерностью 4х4 возможны следующие случаи. В первой строке заполнены все клетки (табл. 3):

Таблица 3

В этом случае с учетом произвольности заполнения строк ниже первой и выбора места для заполненной строки получаем число планов 4х4х4х4=256.

Если в первой строке 3 заполненные ячейки, а во второй 2, получим (табл. 4), что таких заполнений будет 4х3х4х4=192, а с учетом того, что для строчки с тремя заполнениями 4 варианта, а для строчки с двумя заполнениями 3, получим 192х4х3=2304.

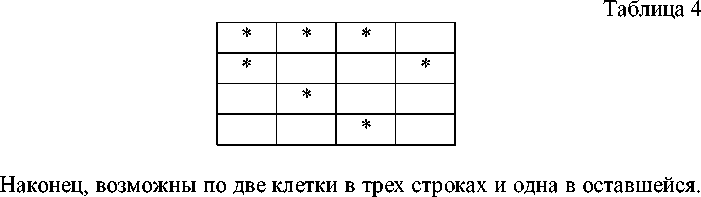
Здесь возможны 2 частных случая, когда заполненные клетки в первых двух строках расположены в разных столбцах (табл. 5) либо имеют общий столбец (табл. 6).

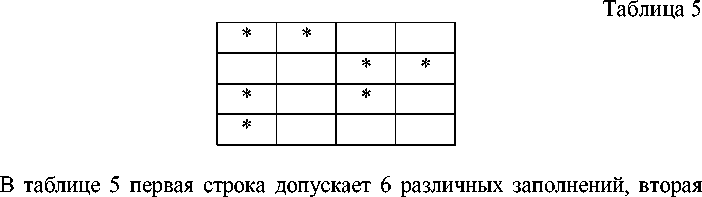
одно, третья 4, а четвертая 4. С учетом произвольного расположения строки с одной заполненной клеткой получаем 6х1х4х4х4x3=1152 варианта.

В таблице 6 первая строка дает 6 разных заполнений, вторая 4, третья 3, четвертая 4. Как и в таблице 5, произведение этих чисел нужно умножить на 4: 6x4x1x4x4=384 варианта. Итого, складывая различные варианты заполнения, получаем N₄=4096.

Аналогичный подробный подсчет для случая задачи 5х5 дает N5=393625, а для случая 6х6 N6=63943456.

Можно проводить подсчет допустимых планов и без их классификации, как это сделано выше. Например, для задач 3х3 и 4х4 могут быть использованы формулы (1)-(3), в которых N0=2N-1, а N=3,4,5 соответственно:

N 0 - 2

N3= £ N !

i = 1

E min( N , N 0 - 1 - i ) j = max(1,( N 0 - i - 1))

min( N , N 0 - i - j ))

∑

k = max(1,( N 0 - i - j ))

N !

k !( N - k )!

j !( N - j )!

i !( N - i )!

min( 1,( N 0 - k - i - j ))

N 0 - 3

N4= £ N !

i = 1

E min( N , N 0 - 2 - i )

j = max(1,( N 0 - i - 2))

min( N , N 0 - 1 - i - j ))

∑

k = max(1,( N 0 - i - j - 1))

∑

l = max(1,( N 0 - i

N !

- j )) l !( N - 1 )!

k !( N - k )!

j !( N - j )!

i !( N - i )!

min(1,( N 0 - 1 - k - i - j ))

S l

где

N 0 - 4

N5= £ n !

i = 1

Y¹ min( N , N 0-3- i ) ^£ j = max(1,( N 0 - i - 2))

min( N , N 0 - 2 - i - j ))

∑ k=max(1,( N 0-i - j-2))

∑ l=max(1,(N0-1-i-j)) l!(N   l)!

k !( N - k )!

j !( N - j )!

i !( N - i )!

S l =

mi 0 - i - j - k - 1 ))

∑

m = max(1,( N 0 - i - j - k - 1 ))

N !

l !( N - 1 )!

Определяемые формулами (1)-(3) (здесь N0=2*n-1 для квадратных матриц при n=m (в общем случае при n^m: N0=n*m-1)) значения для полного числа допустимых планов N_k несколько завышены, поскольку не очищены от возможных циклов, однако результаты расчетов даже в таком виде обнаруживают тесную связь с проделанными выше с помощью анализа таблиц 1-6 (коэффициент линейной корреляции логарифмов количеств планов по этим двум методикам r = 0.997).

Анализ полученных результатов показывает, что логарифмы величин Nk с ростом k растут чуть быстрее линейной функции с тенденцией выхода на линейную зависимость. Это означает, что сама величина Nk стремится к экспоненциальному росту с увеличением размерности задачи.

Отметим, что существует аналогия между транспортными задачами и двудольными графами. Если рассматривать множества поставщиков и потребителей как вершины левой и правой половин двудольного графа, а ребра, соединяющие их, как маршруты перевозок, то можно установить соответствие ТЗ и двудольного графа.

Действительно ребра соединяют только поставщиков и потребителей, нет висячих вершин, не имеющих ребер, а тарифы можно задать как длины ребер, если рассматривать последние как дуги, то есть имеющие направленность от поставщиков к потребителям. Важное для ТЗ условие отсутствия циклов можно ввести, если рассматривать только деревья на таких двудольных графах. На рисунке 4 показаны транспортная таблица с одним из возможных планов и соответствующие ему двудольный граф и дерево.

В этих условиях задача определения числа допустимых планов сводится к подсчету числа деревьев в двудольном графе. Следуя идее Прюфера [9; 10], используемой для доказательства теоремы Кэли о числе деревьев [9; 10], составим код дерева, представленного на рисунке 4. Код данного дерева b₃a₃a₂b₂b₂a i .

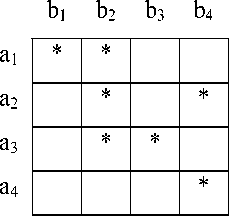
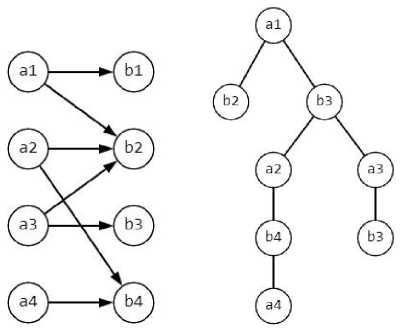
Рис. 4. Транспортная задача и ее граф

В его записи участвовали две группы вершин из разных долей двудольного графа, по четыре вершины в каждой доле. Поэтому число таких кодов, а значит, и деревьев, равно 46. Для произвольного k получаем k2k-2. В силу упоминавшегося выше соответствия допустимых планов ТЗ и деревьев двудольного графа получаем выражение для числа планов ТЗ:

N k = k ^2k~2 .                                          (4)

Заметим, что расчеты по формуле (4) совпадают с полученными ранее оценками для числа допустимых планов ТЗ.

Для случая ТЗ с прямоугольной таблицей имеем двудольный граф с разным числом вершин в долях. В этом случае для n поставщиков и m потребителей имеем:

N nm =n^m-1× m^n-1. (5)

Ранее отмечалось, что для задачи размерности 2х3 число допустимых планов равно 12. Аналогично тому, как это сделано выше для квадратных транспортных таблиц, нетрудно найти, что для задачи 2х5 найдется 80, а для задачи 3х4 432 допустимых плана. Расчет по формуле (5) подтверждает эти значения.

Выводы

В работе проанализированы количественные и качественные характеристики множества допустимых планов ТЗ, которые могут быть полезны при решении различных типов ТЗ, а также при оценке числа базисных планов конкретной ТЗ в модифицированной постановке, отличной от классической.