Достаточные условия асимптотической устойчивости общей разностной системы

В работе доказаны некоторые достаточные признаки асимптотической устойчивости нулевого решения разностной системы с запаздываниями к х„ -^AfX^, где Д. - действительные матрицы (1 51 < к). Как следствия, i=l найдены условия устойчивости разностной системы хп = Ахп_х + Вхп_к, где А,В- действительные матрицы, натуральное число к - запаздывание. Полученные результаты проиллюстрированы на примерах.

Рассмотрим полную разностную систему порядка к . к хп — ^ Axn-i ’

>=1

где A_i - действительные матрицы размера (mxm), х_п: N -> R^m . Наша цель - найти достаточные признаки устойчивости системы (1), легко применимые на практике.

Для аналогичного скалярного уравнения

к

Хп^У^пЧ,                          (2)

<=1

где a, &R (1 < z < ^), известен результат Кона [1], из которого следует, что уравнение (2) асимптотически устойчиво, если

к

В работах [2-4] найдены некоторые простые признаки устойчивости уравнения (2), основанные на ограничениях на коэффициенты сц (\

Результат, полученный Лизом [2], заключается в том, для асимптотической устойчивости уравнения (2) достаточно выполнения условия

к

к

к

(=2

i=2 У :=2 к i=2

где а* =тах{0,а₍}, а_х = max {0,-а/}.

Березанский и Браверман доказали, что уравнение (2) асимптотически устойчиво, если существует такое множество индексов I с {2,3,..., к^, что 0<-a_v-'£a_i<\, iel

2=1

Наша первая задача - получить признак асимптотической устойчивости уравнения (1), аналогичный условию Кона (3). Вторая задача - перенести на систему (1) достаточные признаки устойчивости для скалярного уравнения (2). Третья задача - доказать некоторые дополнительные признаки асимптотической устойчивости, зависящие от четности или нечетности запаздывания. И, наконец, последняя задача - применить полученные результаты к исследованию асимптотической устойчивости системы xn = Axn^+Bxn_k,

где А, В - действительные матрицы размера (т х m), x_n: N -> R^m, keN - запаздывание.

В дальнейших рассуждениях под ||-|| будем понимать любую матричную норму, удовлетворяющую четырем аксиомам нормы:

1.    ||4>0 и p||-0oJ = 0, 2.    |{с.Л|| = |с| • ||Л| для любого с е R, 3.    |j + s||<|4 + ||s||, 4.    ||^Б|| < ЦлЦ • |^| для всех матриц А, В размера (т х т);

и согласованную с некоторой векторной нормой ][-][,, т.е. Ц^Ц* <|р||■ ||x||_t, для любого хе R^m и любой матрицы А размера (т х т).

Определим, как принято, ||Д = max_lsysm ^| a_y |, ЦлЦ^ = max_1S15m £| а_у |.

Следующая теорема является аналогом условия Кона (3) для линейной системы (1).

Теорема 1. Если

к

ЁМ<1> г=1

то уравнение (1) асимптотически устойчиво.

kh УЛ^хпч ^^а^ =«м^{< м}.

Тогда для всех п = к, к +1,... , 2к -1

IIх» II = 2 Ax»-i ^ 2liAVм=«^ <аМ •

Таким же образом, для п > rk, reN, получаем, что ||х„ || <  а^гМ.

Значит уравнение асимптотически устойчиво. Теорема 1 доказана.

Следствие 2. Если |^|| + |в| < 1, то уравнение (4) асимптотически устойчиво.

0,5 -0,3)     <0,2 -0,1)

Пример. Рассмотрим систему (4) с матрицами ⁼ I q 2 0 4 J ’ ^ ⁼ 1^ 0   0 1

. Тогда

Ц^^ ⁺ PIL = L2 > 1, но pllj + Ц^Ц] = 0,9 < 1. Следовательно, согласно следствию 2, уравнение асимптотически устойчиво при любых значениях запаздывания к .

Теорема 3. Если существует натуральное число р (1<р<к') и множество индексов Iс.^р,р + 1,...,к), таких, что,

Математика то уравнение (1) асимптотически устойчиво.

Доказательство. Уравнение (1) можно записать в виде

^ХП “ 2 А^ХП-р “ 5^ A ^^ХП~Р ^{— Х}П-1 ) "^ S А^ХП-1 iel            iel                       iel

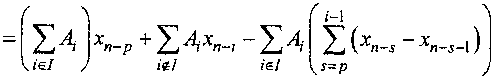
Здесь Е - единичная матрица.

Применяя теорему 1 к (9), получаем требуемое неравенство. Теорема 3 доказана.

Если взять р = 1,1 = {1, Аг}, то из теоремы 3 получим следующий результат.

Следствие 4. Если р + 5|| + ||S|(A - 1)(||Л - £|| + ||Л||) < 1, то уравнение (4) асимптотически устойчиво.

Этот результат удобен для применения, если ||Л - £||«: 1 и |В||«: 1.

Теорема 5. Если существует натуральное число р (1 <  р < к) и множество I

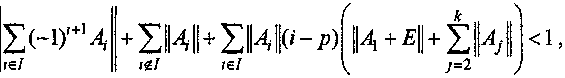
то уравнение (1) асимптотически устойчиво.

Доказательство. Пусть I = 1_ги1₂, где 1_г и 1₂ - множества нечетных и четных индексов соот

(Ю)

индексов

(И)

ветственно.

Предположим, что р - нечетное. Тогда уравнение (1) можно записать в виде хп = Z Ахп-Р - £ Ахп-Р -ЦА(хп-р х»--)+ Z А(Х^Р + х^) + XАхп-. iel}              iel2              iel\                           iel2                           ,6^

~ A ~ S A ^xn-p ^^A^n-i

_Kiel_v iel₂ J it!

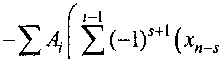
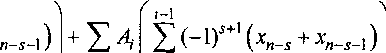
У ^ieI2 V^S=P                       7

+^-94 "У.ИГ’ (4 +£)^.,_,

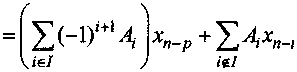
ie]

2 ^,^x«-s-j

Согласно теореме 1 и (12) получаем требуемое утверждение.

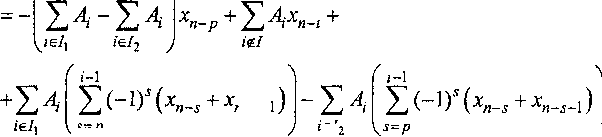
П-5-1

!е/2

V=P

k/e/           / zgZ

+Z(-'r'4 Zt-D* (4+£);„-.-! + f ^.-.-/ iel          \$=p k                  у=2

Как и в предыдущем случае, получаем требуемое утверждение.

Теорема 5 доказана.

Замечание . Если / = 0 или/ = {/>}, то условия (8) и (И) совпадают с условием (7). Если I = {/},/ * р , то получаем более сильные ограничения чем (7).

Если взять р = 1,1 = {1,/}, то теорема 5 дает следующий результат, зависящий от четности или нечетности запаздывания.

Следствие 6. Если

|| Л + (-1/⁺¹ л| + ||В|| (к -1) (|| Л + Е\\ + ||Б||) < 1,                            (14)

то уравнение (4) асимптотически устойчиво.

Этот результат удобен для применения, если ||Л + ЕЦ«: 1 и ||S|| «: 1.

f-0,95 0,01)     f-0,2   0 )

Пример. Рассмотрим систему (4) с матрицами Л = I $     0 96 ] ’ ~ [ 0    0 18)'

Для любой матричной нормы ||Л|| + ||S|| >  р(А) + р(В) = 1,16 > 1. Здесь р(Л) и р(В) - спектральные радиусы матриц. Следовательно, следствие 2 неприменимо к исследованию асимптотической устойчивости данной системы.

Следствие 4 тоже не дает ответа об устойчивости, поскольку ||Л + В^ > р^А + В) = 1,15 > 1.

При нечетных значениях запаздывания к неравенство (14) не выполняется, а при четных значениях к имеем 11Л-Л|| + ||S|| (£-1)(||Л + £|| +||S|| ) = 0,78 +(£-1)0,052 . Отсюда получаем, что уравнение асимптотически устойчиво при к = 1 и к = 4, согласно следствию 6.