Достаточные условия устойчивости линейных систем

А. Ф. Зубова, И. В. Зубов, В. И. Зубов, С. В. Зубов, М. В. Стрекопытова

В данной статье предлагается сводить решение любой вычислительной задачи к построению системы дифференциальных уравнений; все решения или часть их сходятся к решению исходной вычислительной задачи. Далее задача сведется к численному интегрированию полученной системы.

При компьютерном моделировании пренебрежение наличием инвариантных множеств может привести к принципиально неверным прогнозам динамики системы. Прогнозирование состояния системы, сделанное с помощью компьютера, может иметь приемлемую точность, если дискретизованная модель сохраняет основные структурные особенности моделируемой системы, в число которых входят наличие стационарных и нестационарных инвариантных множеств, их свойства и характер предельного поведения траекторий системы. Все это требует тщательного аналитического исследования уравнений динамики для обнаружения этих свойств. Кроме того, сами алгоритмы дискретизации требуют такого их изменения, чтобы указанные структурные свойства непрерывной модели сохранялись и у дискретной модели, уже пригодной для компьютерной реализации.

Постановка задачи

Поставим задачу определения и анализа корней уравнения det(A - ХЕ) = 0,          (1)

где Л - (и х и) — матрица. Известно, что вопрос об устойчивости линейной системы обыкновенных дифференциальных уравнений будет решен, если выяснится, что корни уравнения (1) лежат в левой полуплоскости комплексного переменного Х . Следуя [1], отобразим эту левую полуплоскость на единичный круг в плоскости переменного р при помощи преобразования

X =      •                 (2)

Р ⁺ 1

При этом корни уравнения (1) перейдут в корни уравнения det (В — рЕ) = 0,           (3)

где В = Е + 2 ( А - Е ) '.

Обозначим корни этого уравнения через Р1, р2, ..., ри. Из нашего преобразования следует, что если корни уравнения (1) лежат в левой полуплоскости, то корни уравнения (3) лежат в единичном круге. А тогда, по- скольку матрица Вк имеет собственные чис-

_к к к ла Pi , р ,■■■, Рп, необходимым и достаточным условием асимптотической устойчивости будет условие

В^к ^ 0.              (4)

к ^^

Рассмотрим теперь матрицу В*В^ Эта матрица является симметричной, ее собственные числа неотрицательны^ Обозначим собственные числа матрицы В В через pt, р2> ■■■, Рп Пусть р — наибольшее из этих чисел^ Заметим, что из условия ру < 1 (/ =!,■■■, п)не следует р- < 1 (г = 1, ■■■, п)^ Однако при выполнении условия р- < 1 (г = 1, ■■■, п)

то собственные числа матрицы В лежат в единичном круге^ Следовательно, система с матрицей А асимптотически устойчива^

Доказательство. Вычислим отношение

SJSV.

к к          к

^к = pi + р2 + ■■■ + рп ^1   Pi + р2 + ■■■ + Рп k-1 (1 + (р2/Р1 )k + •••)

¹    ( ^{1 + (} Р 2/^р3 ⁺ ■■■ )

Поскольку р — наибольшее собственное число (здесь мы предполагаем, что матрица В*В имеет хотя бы одно ненулевое собственное число), то справедливы оценки обязательно выполняется и условие рг- < 1 (г = 1, ■■■, n)■

При выполнении условия р- <  1 (г = 1, ■■■, ■ ■■, п) существует целое положительное число к такое, что собственные числа матрицы

k - 1

< S t <  р¹ и S

( В*В^ верно,

ном к

меньше единицьк Обратное также если в некотором целом положитель-собственные числа матрицы | В*В^

меньше единицы, то собственные числа матрицы В лежат в единичном круге, ке^ имеет место асимптотическая устойчивость

По определению

II В1

В       Х*В*ВХ

= max = max---—--- Х е Еп ||Х|| Х е Еп     ||Х||

Введем в рассмотрение величины

Отсюда видно, что при выполнении условия (5) будет справедливо неравенство р' ¹ < 1

Следовательно, наибольшее собственное значение матрицы В В меньше единицы, а тогда выполнено условие (4), откуда следует, что собственные числа матрицы В лежат в единичном круге^ Теорема доказана^

Выводы. Теорема является критерием устойчивости линейных систем^ Как уже было отмечено выше, даже при условии | р у <  1 матрица В*В может иметь собственные числа, превосходящие единицу^ Для того чтобы охватить и эти случаи, следует рассматривать вместо матрицы В * В матрицу

Sk

= s

Sp

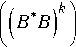
| В * в ) , где т > 1. Условия теоремы останутся прежними Для большей эффективно

I -

I -

Теорема. Если при некотором целом положительном к выполнено неравенство

Sk1

2< <’

S1

сти вычислений можно сразу рассматривать

* т матрицу IВ В1 , где т достаточно велико^ Следует отметить также, что настоящий критерий является достаточным^