Дробное итерирование аналитических в единичном круге функций с вещественными коэффициентами

Пусть P — совокупность всех голоморфных отображений f единичного круга D = = { z G C: | z | < 1 } в себя. Тогда P представляет собой топологическую полугруппу относительно операции композиции и топологии локально равномерной в D сходимости, роль единицы в которой играет тождественное преобразование f (z) = z. Заметим, что P содержит подгруппу I дробно-линейных преобразований единичного круга D на себя. Пусть L — некоторая подполугруппа полугруппы P .

Определение 1. Отображение t ^ f t , действующее из аддитивной полугруппы R + = = {t G R: t ^ 0 } в полугруппу L, называется однопараметрической полугруппой в L, если выполняются следующие условия:

Известно, что всякая однопараметрическая полугруппа t ^ f t в L дифференцируема по t [7] и характеризуется своей инфинитезимальной образующей

• с)

df t (z)    = v(z)

^dt       t =0

посредством дифференциального уравнения a ,

-f t (z) = v(f t (z))                                    (1)

с начальным условием f t (z) | _t = ₀ = z.

Определение 2. Функция f G L вложима в однопараметрическую полугруппу в L, если существует такая однопараметрическая полугруппа t ^ f t в L, что f ¹ = f.

Поскольку семейство { f t } _t > ₀ обладает свойством ii), то f t при целых неотрицательных значениях t — есть натуральные итерации f n = f о f n ^-1 , n = 2, 3,..., функции f = f 1 , а f t , t ^ 0, называют дробными итерациями функции f.

Проблема вложимости, или, по-другому, проблема дробного итерирования имеет два аспекта: вопрос существования дробных итераций и вопрос способа их построения. Отметим, что общая проблема дробного итерирования имеет длительную историю, и ее решение во многом зависит от того, в каком классе функций она рассматривается. Исторически в ее исследовании выделяются три случая: локальный случай (см.: [14], [11]), когда областью определения функции является окрестность неподвижной точки; случай мероморфных функций (см.: [6], [10]), когда областью определения является вся комплексная плоскость, за исключением изолированных особых точек — полюсов; случай аналитических в некоторой области функций, принимающих значения из этой же области [обычно в качестве такой области выбирается единичный круг D (см. [8]) или полуплоскость]. В отличие от первых двух, третий случай более разнообразен по методам и результатам, что связано как с требованием принадлежности дробных итераций классу функций с заданными свойствами, так и с наличием неподвижных точек аналитической функции.

Если f G P \ I, то по теореме Данжуа — Вольфа (см., например, [2]) существует единственная точка q, |q| < 1, такая, что fn(z) ^ q локально равномерно в D при n ^ то. При этом, если q располагается внутри единичного круга D, то f (q) = q, то есть q является неподвижной точкой функции f. В случае, когда q располагается на границе единичного круга D, то есть лежит на единичной окружности T = {z G C: |z| = 1}, то в этой точке существуют угловые пределы f (q) = lim f (z) , f ‘(q) = lim f ‘ (z) = lim —---q . z^q                z^q        z^q z — q

Кроме того, f (q) = q и 0 < f ‘ (q) <  1, то есть q является граничной неподвижной притягивающей точкой. Точка q называется точкой Данжуа — Вольфа функции f и она является общей для всех итераций этой функции. Отметим, что в силу принципа гиперболической метрики (см., например, [5]) все другие неподвижные точки функции f, если они есть, лежат на единичной окружности T.

В зависимости от того, является ли точка Данжуа — Вольфа функции f внутренней или граничной, исследование проблемы дробного итерирования связано с функциональными уравнениями Шре¨ дера и Абеля, соответственно, и их решениями, посредством которых могут определяться дробные итерации.

В данной работе проблема дробного итерирования рассматривается в классе P r [0], который представляет собой совокупность функций f G P , сохраняющих начало координат и имеющих вещественные коэффициенты разложения в ряд Маклорена, то есть

P r [0] = {f G P : f (0) = 0, f ⁽ⁿ⁾ (0) G R, n = 1, 2,... } .

Через E ( P r [0]) будем обозначать совокупность функций f G P r [0], вложимых в однопараметрическую полугруппу в P r [0].

Пусть f Е P \ I, f (0) = 0 и f‘(0) = 0, тогда (см., например, [2]) существует предел f n(z) F(z) = llm n, n^- (f‘(0))

который представляет собой непостоянную аналитическую в единичном круге D функцию, являющуюся единственным решением функционального уравнения Шре¨дера

F (f (z)) = f ‘ (0)F (z)                                   (2)

в классе аналитических в D функций с нормировкой F (0) = 0, F ‘ (0) = 1. Функция F называется функцией Ке¨ нигса и может служить для получения натуральных итераций порождающей ее функции как решений функционального уравнения

F (f n (z)) = (f ‘ (0)) n F (z).

Допустим теперь, что t ^ ft — однопараметрическая полугруппа в Pr [0]. В силу единственности решения задачи Коши (1) функции ft, t > 0, однолистны в D и, следовательно, (ft)’ (0) = 0 (здесь и далее запись (ft)’ (0) означает производную функции f t (z) по переменной z, вычисленную в точке z = 0). Поэтому (см. [2]) можно определить функцию Ке¨ нигса F следующим образом f t(z)

F(z) = lim -—-г——, t^ (f t)’ (0), и она будет общей для всех ft, t > 0. Непостоянная функция F, как предел последовательности однолистных функций, также является однолистной и удовлетворяет функциональному уравнению Шре¨дера

F (f 4z)) = (f t ) ‘ (0) F (z).                                (3)

В данной работе получено интегральное представление класса функций Ке¨ нигса, отвечающих однопараметрическим полугруппам в P r [0]. Отметим, что интегральное представление общего класса функций Ке¨ нигса, отвечающих однопараметрическим полугруппам в P с точкой Данжуа — Вольфа q Е D, получено в [4]. Также найдены необходимые условия вложимости функции f (z) = c 1 z + c ₂ z ² + c ₃ z³ + ... из P r [0] в однопараметрическую полугруппу в P r [0] в терминах ее первых трех коэффициентов с 1 ,с ₂ ,с з . Для f Е E ( P r [0]) получено аналитическое описание границ области изменения второго и третьего коэффициентов при фиксированном значении первого коэффициента. Определены функции f Е E ( P r [0]), соответствующие граничным точкам этой области.

Пусть v — инфинитезимальная образующая однопараметрической полугруппы t ^ ^ f t в P r [0]. Получим равенство, связывающее функцию Кенигса F однопараметрической полугруппы t ^ f t в P r [0] и ее инфинитезимальную образующую v.

Дифференцируя (1) по z и полагая z = 0, получаем дифференциальное уравнение dt (f ^t ) ‘ (0) = v ‘ (0) (f ^t ) ‘ (0)

с начальным условием (f t ) (0) | _{t =0} = 1, интегрирование которого по t приводит к равенству (f t ) (0) = e ^{v (0)t} . Таким образом, уравнение (3) можно записать в виде

F (f t (z)) = e v ^(0)t F (z).

Дифференцируя последнее равенство по t и полагая t = 0, получаем соотношение, связывающее функцию Ке¨ нигса F и инфинитезимальную образующую v

F ‘ (z) v(z) = v ‘ (0) F (z). (4)

Вид инфинитезимальной образующей v однопараметрической полугруппы t ^ f t в P r [0] следует из результата Левнера [12] с учетом вещественности коэффициентов функций из P r [0]:

v(z) = — azp(z), (5) где а >  0 и р Е C r . Под классом C r понимается совокупность аналитических в единичном круге D функций р, удовлетворяющих условиям: V z Е D Re p(z) > 0, р(0) = 1, и производные p ⁽ⁿ⁾ (0) Е R, n = 1, 2,... Ясно, что C r С C , где C — класс Каратеодори аналитических в единичном круге D функций h с положительной вещественной частью и нормировкой h(0) = 1.

Следует отметить, что поскольку необходимым условием вложимости функции f Е Е L в однопараметрическую полугруппу в L является однолистность функции f , то равенство f ‘ (0) = 0 влечет невложимость этой функции. При этом любая функция f Е P r [0], для которой f ‘ (0) < 0, не вложима в однопараметрическую полугруппу в P r [0], так как в этом случае невозможно выполнение соотношения (f t ) (0) ^ 1, при t ^ 0, которое является следствием условия iii), без нарушения необходимого условия однолистности.

Следующая теорема дает интегральное представление класса функций Ке¨ нигса, соответствующих функциям f Е E ( P r [0]).

Теорема 1. Пусть f Е E ( P r [0]) , тогда ее функция Кенигса F имеет вид

F (z) = z exp<

/

ln

[-1 , 1]

1 — 2xz + z ²

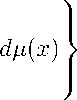
с некоторой вероятностной мерой ц на [ — 1,1] . При этом под логарифмом понимается непрерывная ветвь, принимающая значение 0 при z = 0 .

Обратно, всякая функция F вида (6) является функцией Ке¨нигса для функций f Е E (Pr [0]), определяемых из равенства f (z) = F-1 (eF (z)), 0 <в< 1.

Доказательство. Пусть t ^ ft — нетривиальная (ft(z) ^ z при t > 0) однопараметрическая полугруппа в Pr[0] и F — ее функция Кенигса. Покажем, что функция F допускает представление (6) с некоторой вероятностной мерой ц на [—1,1]. Так как F однолистна в единичном круге D и F(0) = 0, F‘(0) = 1, то функция F(z)/z не обращается в нуль в D и можно выделить однозначную ветвь логарифма ln (F (z)/z), которая обращается в нуль при z = 0. Применяя равенство (4), получаем d- in F dz z

= 1 /zv(O) — A , z    v ( z )

Поскольку вместе с любой функцией р Е C r и функция 1 /р Е C r , то инфинитезимальную образующую (5) можно записать в виде

v ( z ) =

— az

P(z) .

Тогда

v ‘ (0) = —a

и

z v ‘ (0) ^v(z)

^^^^^^^^^r

1 = p ( z ) — 1 .

Следовательно,

-d In FM dz z

= ^{1 (}P^{( z ) —} 1).

Воспользуемся теперь интегральным представлением функций p G C r (см., например, [3, с. 516–518]):

p(z) = у 1

[-1 , 1]

1 — z ²

— 2xz + z ² d^M(x) ’

где ц — вероятностная мера на [ — 1,1]. Тогда дифференциальное соотношение для функ-

ции Ке¨ нигса можно преобразовать

к следующему виду

d dz ln

F (z)

z

=2/1

[-1 , 1]

x — z

— 2xz + z²

d^(x).

Интегрируя последнее равенство

по

zи

учитывая выбор ветви логарифма, получаем

ln F« z

= / ln [-1 , 1]

-—_o¹ , ₂ dM^(x).

1 — 2xz + z ²

Потенцируя это равенство, приходим к формуле (6) для функции Ке¨ нигса, и необходимость доказана.

Для доказательства достаточности покажем, что при любой вероятностной мере ц на [ — 1,1] формула (6) определяет функцию Кенигса некоторой однопараметрической полугруппы t ^ f t в P r [0]. Дифференцируя равенство (6), получаем, что

F ‘(z)= Г z F(z)     J 1

[-1 , 1]

1 — z ²

— 2xz + z ²

d^(x)

есть функция из класса Cr. Таким образом, Re zz "Fv)} > 0 при z G D и, значит, (см., например: [3], [13]) функция F является звездообразной в единичном круге D, то есть она однолистна в D и отображает D на область, которая с каждой точкой F(z), z G D, содержит отрезок {w(t) = tF(z): 0 < t < 1}. Это свойство функции F позволяет определить семейство {ft}t>0 следующим образом f t(z) = F-1 (e-t F (z)

при всех t ^ 0.

Непосредственно из (6) следует, что F (0) = 0, F ‘ (0) = 1 и производные F ⁽ⁿ⁾ (0) G

G R, n = 2, 3,.

.

., поэтому f t G Pr [0] и (f t) (0) > 0 при всех t > 0. Кроме того, функции семейства {ft}t>0 образуют однопараметрическую полугруппу в Pr [0], поскольку условия i),iii) выполнены и для любых s, t ^ 0 имеем ft+s (z) = F-1 (>(t+s)F (z)) = F-1 (e-t e-sF (z)) =

= F ^-1 (e ^-t F о F ^{-1 (} e ^-s F(z) ⁾⁾ =

= F ^-1 (e ^-t F (f ^s (z))) = f t о f ^s (z).

Остается показать, что функция F вида (6) является функцией Ке¨ нигса однопараметрической полугруппы t ^ ft в Pr [0]. Действительно, lim t→∞

f t (z)

(f t ) ' (0)

_r   f t(z)    ..   F ^-1 (e ^-t F (z))

= lim —— = lim----—----= t→∞ e-t    t→∞      e-t r F-1 (e-t F(z)) F(z) lim-----------, _., x-------- t^^      e tF(z)

= (F -1) '(0) F (z) = F (z).

Теорема 1 доказана.

Полученное в теореме 1 интегральное представление класса функций Ке¨ нигса, соответствующих функциям f G E ( P r [0]), позволяет найти некоторые необходимые условия вложимости функции f G P r [0] в однопараметрическую полугруппу в P r [0] в терминах оценок ее начальных коэффициентов.

Выделим в пространстве R ² множество C (c _i ) следующим образом:

^{C (c} 1 ) = {^(c 2 , ^c 3 ) ^{G R} 2 ^{: f (z)} = c i z + c 2 z ² + c 3 ^z 3 + . . . , ^{f G E (} P r ^[0])} .

Отметим, что c _i G (0,1] и c _i = 1 только в случае тождественного преобразования f (z) = z. Оценка снизу для коэффициента c _i следует из условия f G E ( P r [0]), а оценка сверху — из леммы Шварца.

Следующая теорема дает аналитическое описание границ множества C (c _i ).

Теорема 2. Пусть c _i G (0,1) фиксировано. Тогда C (c _i ) представляет собой замкнутое множество в R ² , ограниченное кривыми

Y ⁺ (c i ): с з

1 - 3c i 2c i ⁽¹ — c i )

c 2 + C i (1

— cl), где

^{— 2c} 1 ^{(1 —} c l ) C ^c 2 C ^2c 1 ^{(1 —} c l ),

Y (c i )^: с з = — c 2 — C i (1 — c i ) , где  — 2c i (1 — C i ) C C 2 C 2c i (1 — c i ).

Доказательство. Дифференцируя трижды функциональное уравнение Шре¨ дера (2) и учитывая условия F(0) = 0, F'(0) = 1, получаем соотношения для коэффициентов функции f G P \ I, f (0) = 0, f '(0) = 0, c2 = 7^ ci (1 — ci) F''(0),

2                                                                         (8)

c 3 = — 2 c i (1 — c i ) (^c i (F '' (0)) ² — ₃ (1 + c i ) F ''' (0) j .

Далее, дифференцируя равенство (6), получаем соотношение

F ' (z)      , .

z F(z)    P(z), где p Е Cr, трехкратное дифференцирование которого с учетом условий F(0) = 0, F‘(0) = = 1 приводит к следующим равенствам:

F "(0) = 2 p ‘ (0),

F ‘‘‘ (0)=3(р ‘ (0)) 2 + 3 р ‘‘ (0).

Подставляя (9) в соотношения (8), получаем, что начальные коэффициенты функции f Е E ( P r [0]) имеют вид

С2 = С1 (1 - С1) p‘(0), сз = 4 ci(1 — ci) ((2 — 6 ci) (p‘(0)) + (1 + ci)p‘‘(0)).

Определим теперь область значений { p ‘ (0), р ‘‘ (0) } . Заметим, что для любых функций p ∈ C r и h ∈ C справедливо соотношение

p(z)=2 (h(z)+h(z)).

Используя это соотношение, а также интегральное представление функций h ∈ C (см., например, [13]):

h ( z ) =

1 + K Z

1 — K z

dv (к) ,

T где ν — вероятностная мера на единичной окружности T, получаем p‘(0) = 2Re Yi, p‘‘(0) = 4 Re 72,

где γ ₁ , γ ₂ — первый и второй моменты функции h ∈ C

7 1 = к dv ( k ) , 7 2 = k ² dv ( k )

TT

Область взаимного изменения моментов γ ₁ и γ ₂ следует из теоремы Каратеодори — Те¨ плица (см., например, [1])

|7i| < 1, |72 — 72| < (1 — Ы2), что может быть записано в виде

7 i = (, 7 2 = 7 12 ⁺ (1 ^— | 7 1 | 2) П,

где I C I <  1, | n | <  1.

Учитывая соотношения (11) и (12), получаем, что при фиксированном p ‘ (0) Е Е [ — 2,2]

max { р ‘‘ (0) } = 4 max {Re 7 2 + (1 — h^² )} = 4, min { p ‘‘ (0) } = 4min {Re7 2 — (1 — | 7 _i | ² )} = 2 (p ‘ (0)) 2 — 4.

Итак, верхняя и нижняя границы области значений { p ‘ (0), р ‘‘ (0) } определяются следующим образом:

р ’’ (0) = 4, где р ‘‘ (0) = 2 (р (0)) ² - 4, где

2 ^ р ‘ (0) ^ 2,

2 ^ р ‘ (0) ^ 2,

соответственно (см. рис. 1).

Подставляя теперь в равенства (10) соотношения (13), получаем уравнения кривых Y + (c 1 ), Y - (c 1 )- Теорема 2 доказана.

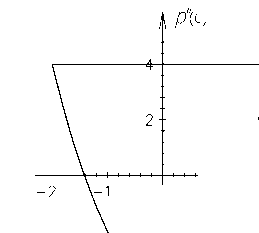
Рис. 1. Область значений { p ‘ (0) , р ’’ (0) }

Поскольку однолистность является необходимым условием вложимости функции, то вопрос о содержательности полученных в теореме 2 оценок начальных коэффициентов функции f G E ( P r [0]) был решен сравнением с соответствующими точными оценками в классе ограниченных однолистных функций с вещественными коэффициентами (см. [15]). Рисунок 2 является иллюстрацией этого сравнения: множество C (c 1 ) вкладывается в соответствующее множество U (c 1 ), построенное по точным оценкам в классе ограниченных однолистных функций с вещественными коэффициентами.

Рис. 2. Соотношение множеств C ( с 1 ) и U ( с 1 ) при с 1 = 0 , 2

Отметим, что в [9] сформулированы необходимые условия вложимости функции f G P[0], то есть f G P, f (0) = 0, в однопараметрическую полугруппу в P[0], а также функции f G Pr [0] в однопараметрическую полугруппу в Pr [0] в терминах первых двух коэффициентов. Однако во втором случае отслеживание только первых двух коэффициентов не дает преимуществ при проверке на вложимость по сравнению с необходимым условием однолистности, поскольку множество C = {(ci, c2) € R2: f (z) = c1z + c2z2 + + ..., f € E(Pr [0])} совпадает с соответствующим множеством в классе ограниченных однолистных функций с вещественными коэффициентами.

Рассмотрим теперь вопрос об экстремальных функциях, то есть выясним, каким функциям f € E ( P r [0]) соответствуют граничные точки множества C (c ₁ ).

Теорема 3. Пусть c ₁ € (0,1) фиксировано и y ⁺ (c ₁ ) , Y - (c ₁ ) ^_ кривые, определенные в теореме 2. Тогда справедливы следующие утверждения:

• 1)    в C (c 1 ) функции f € E ( P r [0]) соответствует точка кривой y ⁺ (c ₁ ) тогда и только тогда, когда

f (z) = F-1 (ci F(z)), где F — функция Ке¨нигса, определяемая по формуле

^{F (z)}    (1 + z) ^1-A (1 - z) ^1+A ’ ^A    2c i (1 - c i ) .

• 2)    в C (c ₁ ) функции f € E ( P r [0]) соответствует точка кривой y (c ₁ ) тогда и только тогда, когда

f (z) = F-1 (C1 F(z)), где F — функция Ке¨нигса, определяемая по формуле

F (z) =

z

1 - 2Az + z ² ’

A =

C 2

^2c 1 ^{(1 — c} 1 )

Доказательство. Пусть функция f € E ( P r [0]) соответствует некоторой точке кривой Y ⁺ (c ₁ ). Тогда ее коэффициенты определяются условиями:

c ₂ € [ - 2c ₁ (1 - c ₁ ), 2c ₁ (1 - c ₁ )],

1 — 3c1    2              2\ c3 = 2С1 (1 — c,) c2 + c1 (1 - C1)'

что следует из теоремы 2. С другой стороны, эти коэффициенты связаны с величинами p‘(0) и p‘‘(0) по формулам (10). Отсюда получаем, что для функции f € E(Pr[0]), соответствующей точке кривой y+ (c1), p‘(0) =    ,. c2    ■, c1 (1 — c1)

, p‘ (0) = 4.

Из интегрального представления (7) функций класса Cr следует, что p‘(0) = 2 У

[-1 , 1]

P ‘‘ (0) = 8 j

[-1 , 1]

x d^(x),

x ² d^(x) — 4.

Таким образом, из последних двух систем получаем

I х dц(x) = A, [-1 , 1]

I x ² dц(x) = 1, .[-1 , 1]

где A = С 2 / (2c 1 (1 - C 1 )).

Из второго равенства системы (16) следует, что вероятностная мера ц на [ — 1,1] сосредоточена в точках ± 1. Действительно, в противном случае нашлись бы 0 < е < 1 и 0 < 5 <  1 такие, что ц ([ — 1 + 5, 1 — 5]) > е. Тогда

У х ² dц(x) = У х ² dц(x) +   Ух ² dц(x) + У х 2 dц(x) ^

[-1 , 1]

[-1, —1+5)

< ^{ц ([ —} 1,

[-1+ 5, 1- 5 ]

(^1- 5, ^1]

— 1 + 5)) + (1 — 5) ² ц ([ — 1 + 5,1 — 5]) + ц ((1 — 5,1]) <

< 1 — е (1 — (1 — 5)2) < 1, но это противоречит второму равенству системы (16).

Итак, ц = (1 — в)5-1 + в51, 0 ^ в ^ 1, где 5-1 — мера Дирака, сосредоточенная в точке — 1, 51 — мера Дирака, сосредоточенная в точке 1, и в = (1 + A)/2, что следует из первого равенства системы (16). Более точно, для функции f G E(Pr [0]), соответствующей точке кривой y + (c1), в представлении функции Ке¨ нигса (6) вероятностная мера µ имеет вид

^{1 — A 1} +^A                 c 2

^ц = — ⁵- ¹ + — ^{5 1} ' где ^A = 2С1(1 — С1) '

Подставляя теперь (17) в (6), получаем формулу (14), по которой определяется функция Кенигса, которая связана с функцией f G E ( P r [0]), соответствующей точке кривой y ⁺ (c 1 ).

Рассуждая аналогично, получаем, что для функции f G E(Pr [0]), соответствующей точке кривой y-(c1), f p«» - c^,

, p"(0) = 2 (p ‘ (0)) ² — 4, что может быть записано следующим образом

У х dц(x) = A, [-1 , 1]

У х ² dц(x) = A ² , .[-1 , 1]

где A = С 2 / (2c 1 (1 — С 1 )).

Рассмотрим меру µ как распределение вероятностей некоторой случайной величины Z. Тогда условия (18) означают, что математическое ожидание EZ = А и дисперсия DZ = EZ 2 - (EZ) 2 = 0. Следовательно, Z почти наверное совпадает с EZ, а мера ц сосредоточена в точке λ.

Итак, для функции f G E(Pr [0]), соответствующей точке кривой y-(c1), в представлении функции Ке¨ нигса (6) вероятностная мера µ есть мера Дирака δ, сосредоточенная в точке λ, c2

^ц    °А, ^{где А} 0/1      \ ’

2c i (1 - c i )

и, значит, сама функция Ке¨ нигса записывается по формуле (15).

Осталось отметить, что в силу уравнения Шредера (2) функция f G E(Pr[0]), соответствующая точке кривой y +(c1) или кривой Y-(c1), определяется по формуле f (z) = F-1 (ci F(z)), где, по доказанному выше, F — функция Ке¨ нигса (14) или (15), соответственно. Необходимость утверждений 1)–2) доказана.

Пусть теперь f G E ( P r [0]) и f (z) = F ^-1 (c 1 F (z)), где F — функция Кенигса, определяемая по формуле (14). Дифференцируя трижды равенство f (z) = F ^-1 (c 1 F (z)), получаем, с учетом условий F (0) = 0, F ‘ (0) = 1, соотношения (8) для коэффициентов функции f. Далее трехкратное дифференцирование функции Ке¨ нигса (14) приводит к равенствам:

F ‘‘ (0) = 4А,

F ‘‘‘(0) = 12 А2 + 6, подставляя которые в (8), получаем, что функция f соответствует точке (c2,c3) G C(c1), где

• ^{1    — 3c} 1    2              2Х

c ³ = 2c i (1 - c i ) c ^{2 +} c ¹ <1 - ^{C 1)} '

то есть точке кривой y ⁺ (c 1 )-

Точно также, пусть f G E ( P r [0]) и f (z) = F ^-1 (c 1 F (z)), где F — функция Ке¨нигса, задаваемая формулой (15). После трехкратного дифференцирования функции Ке¨нигса (15) получаем равенства:

F ‘‘ (0) = 4А,

F‘‘‘(0) = 24А2 - 6, подстановка которых в (8) приводит к тому, что функция f соответствует точке (c2, c3) G

G C (c i ), где

¹    2

c 3 = — c 2

c 1 ²

- c i 1 - c ² _i ,

то есть точке кривой y (c 1 )- Это завершает доказательство достаточности утверждений 1)–2) и теоремы 3.

Отметим, что функция f G E ( P r [0]), соответствующая точке кривой y ⁺ (c 1 ), отображает единичный круг D в себя с симметричными относительно вещественной оси

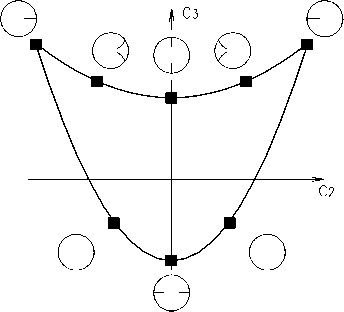
Рис. 3. Экстремальные функции множества C ( c 1 )

разрезами, а функция f G E ( P r [0]), соответствующая точке кривой y - (c 1 ), отображает единичный круг D в себя с разрезами по вещественному диаметру. На рисунке 3 схематично показаны экстремальные функции множества C (c 1 ).

В заключение хотела бы выразить искреннюю благодарность научному руководителю — доктору физико-математических наук, профессору В.В. Горяйнову за помощь в работе, а также доктору физико-математических наук, профессору В.В. Старкову и кандидату физико-математических наук А.А. Полковникову за полезные замечания.