Другой подход к алгебраической классификации электромагнитного поля

Обычно алгебраическая классификация электромагнитного поля связывается с решением характеристического алгебраического уравнения 4-го порядка при постановке задачи па. собственные значения для антисимметричного тензора, электромагнитного поля в пространства Минковского (см., например, [1]- [2])

А⁴ + I 1 A 2 - I2 = 0,

(0.1)

где А - собственные значения тензора, электромагнитного поля F _ae- I 1 = F _ae F^ав 11 I 2 = F_ae F^ав суть соответственно инварианты электромагнитного поля, греческие индексы пробегают значения 0,1,2, 3, звезд очка * обозначает дуальное сопряжение в пространстве-времени Минковского.

1|(1)(1)(1)(1)|

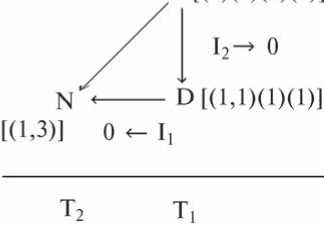
Рис. 1. Диаграмма алгебраической классификации электромагнитного поля для задачи на собственные значения тензора электромагнитного поля по аналогии с алгебраической классификации Петрова.

В итоге, электромагнитное поле может быть проклассифицировано по алгебраическим типам по аналогии с подходом Петрова, к классификации гравитационного поля [4]. Результаты такой классификации электромагнитного поля приведены на. рис.1 в виде диаграммы соответствующих связей между алгебраических типов электромагнитного поля [1], введенных по аналогии с классификацией гравитационного поля .

Однако согласно [3] возможно приведение произвольного многочлена. 4-й степени к нормальной форме Вейерштрасса. или кубическому многочлену.

1. Приведение к нормальной форме Вейерштрасса

Рассмотрим сначала многочлен G (А) 4-й степени с произвольными постоянными коэффициентами а₀, а1, а₂, а₃, a₄

G (А) = aoA4 + 4ai А3 + 6а2А2 + 4аз А + a4                           (1.1)

и приведем его к кубическому многочлену согласно процедуре, изложенной в [3], когда один из корней G (А) отображается в бесконечно удаленную точку с помощью дробно-линейного преобразования переменной А.

Пусть а - один из нулей многочлена. G (А) . т.е. G (а) = 0. Введем замену

А = а + 1/X.(1.2)

Подставляя ее в (1.1) и приводя подобные члены с учетом G (а) = 0, получим

G (X) = (1/X4) (4A1X3 + 6A2X2 + 4A3X + A4) ,(1.3)

где коэффициенты A 1 , A 2 , A 3 , A 4 находятся путем дифференцирования исходного многочлена G(А) по А необходимое число раз при А = а:

Gx (а) = 4A1 — 4 (аоа3 + 3а1а2 + 3а2а + аз) ;(1.4)

(1/2!) G" (а) = 6A2 = 6 (а0а2 + 2а1а + а2) ;(1.5)

(1/3!) G"' (а) = 4A3 = 4 (аоа + а1);(1-6)

(1/4!) G(V (а) = A4 = ао.(1.7)

Считая, что A1 = 0 , воспользуемся новой заменой

Л = A1X + A2/2.(1.8)

Если с самого начала в (1.1) потребовать выполнения равенства G (А) = 0 , то после замены переменной приходим к кубическому уравнению, описывающую катастрофу сборки (одну из основных элементарных катастроф [5])

Л3 + рЛ + q = 0.(1.9)

где коэффициенты р и q равны р = -g2/4; q = -дз/4,                                    (1.10)

где д2,дз суть инварианты кривой 4-й степени, равные соответственно g2 = 3A2 — 4A1 A3 = аоа4 + 3а2 — 4aia3;                         (1-11)

a0 a1 a2

а1 а2 а3 I                        (1-12)

a2 a3 a4

Таким образом, окончательная запись кубического уравнения (1.9) зависит лишь от исходных коэффициентов многочлена G (А).

Применим теперь всю эту процедуру к характеристическому уравнению (0.1).

В этом случае а0 = 1; а1 = а3 = 0; 6а2 = I1; а4 = —12. Поэтому для а = 0 получаем g2 = (I2/12 — I2) ; g3 = — (I1/6) • (I2/36 + I2) .                      (1.13)

Дискриминант кубического уравнения (1.9) запишется через инварианты электромагнитного поля в виде

Q = (р/3)² + (q/2)2 = (I₂²/ (63 • 27)) • (4I2 + I2)2                       (1.14)

и всегда будет неотрицателен Q > 0.

Уравнение сепаратрисы задается условием Q = 0 , что эквивалентно обращению в нуль 2-го инварианта электромагнитного поля I 2 (вектор напряженности электрического поля E и вектор индукции магнитного поля B ортогональны). Тогда корни уравнения (1.9) легко находятся и равны

Л1 = -I1/6; Л2 = Лз = -Л1/2 = I1/12.

(1.15)

При этом р = —I2/ (6 • 23) ; q = I?/ (63 • 22) > 0. (1.1G)

Следовательно, полученному решению отвечает ветвь полукубической параболы, отмеченной крестиком на рис.2. Кроме того, при сравнении с решением для уравнения (0.1), когда I 2 = 0 , получаем, что найденное здесь решение соответствует типу D электромагнитного поля, который в таком представлении является аналогом типа D в гравитационном случае [2].

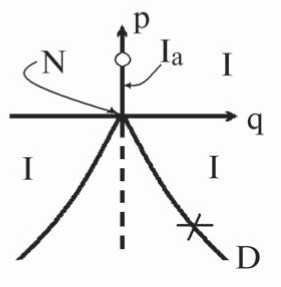
Рис. 2. Проекция катастрофы сборки на плоскость управляющих параметров p и q. Крестиком отмечена ветвь полукубической параболы типа D

В свою очередь, q = 0, р = I 2 /4 при I 1 = 0 (это множество точек помечено кружком на оси р ) и Л1 = 0; Л₂ = —Л? = ^—р. В исходной записи (0.1) имеем (А⁴ — I2) = 0, то есть реализуется алгебраический тип I электромагнитного поля (см., [1]- [2]), хотя по аналогии с алгебраической классификацией гравитационного поля было бы естественней назвать его здесь типом I a [2].

Очевидно, что в точке р = q = 0 (I 1 = I₂ = 0) получаем тип N: чисто волновой алгебраический тип (если векторы E и B не равны тождественно нулю). В этой же точке в приведенном представлении наглядно видно наличие фазового перехода, второго рода (см, [2]).

Если на бесконечность отображается корень уравнения G (А) = 0, равный нулю, то получаем уравнение складки (одну из семи элементарных катастроф [5])

Л² + р = 0. (1.17)

Этот случай отвечает алгебраическому типу D электромагнитного поля (см. также [1]- [2]) и его удобней исследовать для исходной переменной А, тем более что тогда точка бифуркации соответствует типу N и является точкой фазового перехода 2-го рода.

Для максимально общего случая классификации электромагнитного поля (инварианты поля I 1 и I 2 одновременно не равны нулю), связанной с решением уравнений (0.1) и (1.9), имеем наиболее общий алгебраический тип I (см. рис.2).

Вейля с помощью главных световых направлений Дебеве (их может быть не менее одного и не более четырех) и соотношениями между коэффициентами уравнения

Ф0 - 4ЛФ1 + 6Л2Ф2 - 4Л3Ф3 + Л4Ф4 = 0,

(2.1)

где Ф0, Ф1, Ф2, Ф3, Ф4 суть пять комплексных скаляров, связанных с проекциями тензора Вейля на главные снегоподобные направления, задаваемые светоподобиой тетрадой. Корпи этого уравнения в заданной точке пространства-времени определяют алгебраический тип гравитационного поля [6, с.48].

Решение уравнения (2.1) связано с решением кубического уравнения, к которому оно сводится при Ф1 = 0, то есть фактически используется приведение левой части уравнения (2.1) к нормальной форме Вейерштрасса.

С аналогичной ситуацией сталкиваемся при алгебраической классификации электромагнитного поля па. уровне антисимметричного тензора, электромагнитного поля, когда характеристическим уравнением оказывается уравнение четвертой степени переменных, являющихся собственными значениями.

Приведение характеристического уравнения для электромагнитного поля к кубическому характеристическому уравнению (нормальной форме Вейерштрасса) позволяет свести задачу алгебраической классификации электромагнитного поля к задаче, аналогичной классификации Петрова, гравитационного поля. В итоге получаем и аналогичные алгебраические типы электромагнитного поля: I, Ia, D, N.

Анализ полученной классификации электромагнитного поля с точки зрения теории катастроф показывает, что при проекции катастрофы сборки на плоскость управляющих параметров p и q (рис.2) наличие точки фазового перехода второго рода (p = q = 0) соответствует алгебраическому типу N (плоской электромагнитной волны).