Dual Population Genetic Algorithm for Solving Constrained Optimization Problems

Published Online January 2015 in MECS

Genetic algorithms (GAs) are population based search algorithms that obtain solution to optimization and search problems. The problem associated with GAs is that as the populations evolve, they lose diversity and their individuals are trapped in local optima, especially when involving complex problems which have a lot of peaks in the fitness landscape [1]. Literature terms this problem as premature convergence.

One of the proposed solutions for above problem is DPGA. DPGA uses a reserve population along with the main population. This provides additional diversity to the main population. Information exchange between the populations takes place through inter-population crossbreeding. This technique helps to solve the problem of premature convergence [1].

DPGA is used to solve optimization problems. Optimization problems can be classified into Unconstrained Optimization Problems (UOPs) as well as Constrained Optimization Problems (COPs). COPs are encountered in allocation, economics, location, VLSI, engineering and structural design problems [2]. If resources can be made available without any limitation, then there is no limit to the profit that can be achieved. However, in the face of real world complications, resources are most likely to be limited in the form of constraints imposed upon the optimization function. What constitute the difficulties of the constrained optimization problem are the various limits on the decision variables, the constraints involved, the interference among constraints, and the interrelationship between the constraints and the objective function, mass of memory and computation cost [3].

Evolutionary Algorithms (EAs) have been found effective in the solution of a wide variety of optimization and search problems. But EAs are unconstrained search technique therefore incorporating constraints into the fitness function of an EA is an open research area. There is wide scope available for the research regarding mechanisms that allow EAs to deal with equality and inequality constraints [4].

This paper applies a novel method to solve the above research problem. It solves COPs by applying Maximum Constrains Satisfaction Method (MCSM), using DPGA which is an EA. MCSM is a novel technique which tries to satisfy maximum constrains first and then it attempts to optimize objective function.

Section II gives a brief literature review of DPGA and COPs. Section III describes DPGA with implementation details such as fitness function for reserve population and evolutionary process. Section IV presents experimental results and discussion. Section V gives some conclusions and exhibits future scope.

• II.    Literature Review

Dual Population Genetic Algorithm for solving COPs is new in the area of evolutionary algorithms for solving optimization problems. Therefore we have extensively searched in literature about evolution of DPGA. We have also studied nature of COPs and searched methods that solved COPs till date. We have provided brief literature review on DPGA followed by literature review on COPs.

Park and Ruy (2006) [5] proposed DPGA. It has two distinct populations with different evolutionary objectives: The prospect (main) population works like population of the regular genetic algorithm which aims to optimize objective function. The preserver (reserve) population helps to maintain the diversity. Park and Ruy (2007) [6] introduced DPGA-ED that is an improved design-DPGA. Unlike DPGA, the reserve population of DPGA-ED evolves by itself. Park and Ruy (2007) [7] proposed a method to dynamically adjust the distance between the populations using the distance between good parents. Park and Ruy (2007) [8] exhibited DPGA2 that uses two reserve populations. Park and Ruy (2010)  [1]

experimented DPGA on various classes of problems using binary, real-valued, and order-based representations. Umbarkar and Joshi (2013) [9] compared DPGA with OpenMP GA for Multimodal Function Optimization. The results show that the performance of OpenMP GA better than SGA on the basis of execution time and speed up.

The basic and classical constrained optimization methods include penalty function method, Lagrangian method [10] and Sequential Quadratic Programming (SQP) [11]. These are local search methods which can find a local optimal solution.

Recent trend is to make use of evolutionary algorithms to solve constrained optimization problems [12, 13].

Compared with the traditional nonlinear programming approach, evolutionary algorithms need less information such as gradient (derivatives), as well as it is a global searching approach. According to Koziel and Michalewicz [14], these algorithms can he grouped into four categories:

• i.    Methods based on preserving feasibility of solutions by transforming infeasible solutions to feasible solutions with some operators [15]

• ii.    Methods based on penalty functions which introduce a penalty term into the original objective function to penalize constraint violations in order to solve a constrained problem as an unconstrained problem [16] iii. Methods which make a clear distinction between feasible and infeasible solutions [17]

iv. Methods based on evolutionary algorithms [18, 19, 20] v. other hybrid methods combining evolutionary computation techniques with deterministic procedures for numerical optimization [21]

• III.    Dual Population Genetic Algorithm

DPGA starts with two randomly generated populations, the main population and the reserve population. The individuals of each population are evaluated by their own fitness functions. The evolution of each population is obtained by inbreeding between parents from the same population, crossbreeding between parents from different populations, and survival selection among the obtained offspring [1]. In the following paragraphs, the fitness function used for the reserve population, evolutionary process of simple DPGA and methodology applied by this paper are described

• A.    Fitness Function for Reserve Population

The objective function of the problem works as the fitness function of the main population. Fitness function for the reserve population is defined in another way. An individual in the reserve population is given a high fitness value if its average distance from each of the individuals of the main population is large. Therefore the reserve population can provide the main population with additional diversity.

In the equation (1) of the fitness function, each individual of the reserve population can maintain a given distance δ from the individuals of the main population [1, 5, 6].

fr δ ( x ) = 1 - | δ - d ( M , x )|                  (1)

Where, d (M, x): average distance (0 ≤ d(M, x) ≤ 1) between the main population M and individual x of the reserve population

• δ : desired distance (0 ≤ δ ≤ 1) between two population

Assuming a binary representation for a chromosome, d (M, x) is calculated using equation (2) [1, 5]

11 ^l

d ( M , x ) =      ∑ hd ( m , x ) = ∑ | f_Mk - x_k |   (2)

| M | m ∈ M                l k = 1    ^{M , k    k}

Where,

• n : size of main population

• m_i : i th chromosome of the main population

hd(mi, x): Hamming distance between two chromosome vectors m and x l : length of chromosome

• m i, k : k th gene on chromosome m i and x k

• f M,k : frequency of the k th gene value ‘1’ of the main population M

• x i : frequency of k th gene value ‘1’ of the chromosome vector x and is identical to the k th gene value of the chromosome

The definitions of d(M, x) and δ enable fr δ^{(x )} to take a maximum value of 1 when the distance from x to the main population is δ and decreases linearly as d(M, x) deviates from δ [1].

• B.    Evolutionary Process

Firstly, the algorithm selects four parents - two from the main population and two from the reserve population. The parent selection from the main population depends on fitness value calculated by the objective function whereas parent selection from the reserve population depends on fitness value calculated by equation (1) [3].

From four parents, the algorithm generates six offspring by two inbreeding and one crossbreeding processes. Two offspring are generated by mating two parents selected from the main population; another two offspring are generated by mating two parents selected from the reserve population, and yet another two offspring are generated by mating one parent selected from the main population and one parent selected from the reserve population. The above procedure of generation of the new population is represented in the diagrammatic form in fig.1 [1, 6].

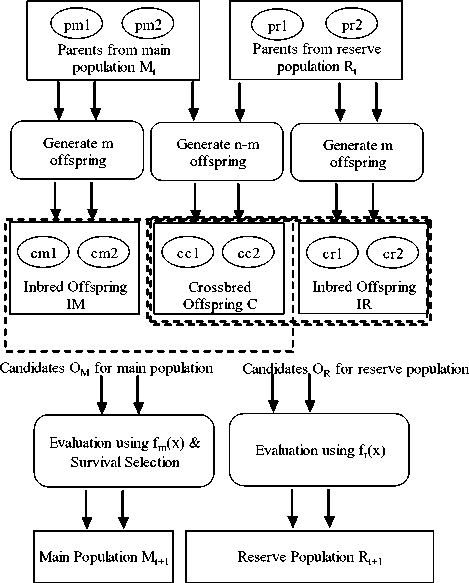
Fig. 1. Procedure for producing new populations

• C.    Methodology

The methodology for applying DPGA for COPs is described in this section. A detailed pseudo code is explained in fig.2 entitled DPGA_MCSM. MCSM is a novel technique. It is based on Deb’s rules that in the category of methods searching for feasible solutions, any feasible solution is better than any infeasible one [20]. According to the first phase of MCSM, Pseudo Random Number Generator (PRNG) selects variables to prepare individuals which satisfy all constrains. As per the second phase of MCSM, DPGA meta-heuristic is applied for evolution of both populations via inbreeding. DPGA evolves till stopping criteria are met.

The algorithm starts with iinitialization of main population M 0 , reserve population R 0 , crossover rate, elitism rate, mutation rate, crossbreeding rate, tour size for tournament selection and max generation t max. The main population of size m and reserve populations of size n, where n > m are initialized using PRNG provided by stdlib.h of C programming language. We check satisfaction of all constraints for current COP in initialization. Both the populations initialize using same constraints on variables.

Firstly, main population undergoes through traditional evolution cycle of Genetic Algorithm. In the first Step I initialized population encoded using IEEE 754 algorithm from decimal value representation to binary value representation. In Step II fitness of main as well as reserve population is calculated using objective function and special fitness function (1), (2) for reserve population.

Step III and IV perform inbreeding of main and reserve population. For selection of the parents, individuals of the main population are sorted according to fitness value. Then according to crossover rate appropriate number of parents gets selected for reproduction. Multipoint crossover method is then used for generating new population called intermediate main population. For evolution of reserve population tournament selection is used. Multipoint crossover method is used to generate intermediate reserve population. Flip bit mutation is used to provide diversity to the intermediate main population and the intermediate reserve population.

In Step V DPGA performs crossbreeding between different populations. Offspring of size (n-m) is generated via crossbreeding on the main population and the reserve population. In crossbreeding (n-m) numbers of best candidates are selected from both populations. Intermediate main population, intermediate reserve population and offspring constitute a candidate set for the next generation of the main population and reserve population. Step VI decodes both populations using IEEE 754 algorithm from binary value representation to decimal value representation. Step VII evaluates generated candidate sets using objective function and fitness function for reserve population. Fitness values are used for survival selection in Step VIII using truncation mechanism. Since m is the number of inbred offspring, the crossbred offspring can survive only when they are better than at least one of the inbred offspring [1].

DPGA evolves till maximum number of generations specified are met or algorithm achieves optimal solution of current COP. These conditions work as stopping criteria for algorithm. Optimum value generated over the given maximum generations is taken as optimal solution for that run.

• IV. Experimental Results and Discussion

  The results are taken on processor AMD FX(tm)-8320 Eight-Core Processor with 3.51 GHz clock speed. The machine equipped with 16GB RAM and hard disk of capacity 500GB with operating system CentOS 6.5.

Standard problems are taken for experiments from “Problem Definitions and Evaluation Criteria for the Congress on Evolutionary Computation 2006 Special Session on Constrained Real-Parameter Optimization problem” (CEC 2006) [22]. In this report, 24 benchmark functions are described. Guidelines for conducting experiments, statistical parameters and its formula, performance evaluation criteria are given at the end of this report.

This test set contains following function characteristics that make our study reliable and robust-

• 1.    Multimodal functions to verify the reliability of the 3. High dimensional functions algorithms

• 2.    Scalable functions

Procedure DPGA_MCSM begin

Initialize main population M 0 , reserve population R 0 , crossover rate, elitism rate, mutation rate, crossbreeding rate, tour size, max generation t max

Initialize M 0 of size m

Initialize R 0 of size n, n>m

• t: = 0

Repeat

Step I: Encode both population using IEEE 754 algorithm from decimal value representation to binary value representation

Step II: Fitness Calculation

• a.    Evaluate M 0 using objective function fm(x)

• b.    Evaluate R 0 using fitness function for reserve population as per equation (1) fr(x)

Step III: Inbreeding of main population

• a.    Selection – using sorting select best fit parents from M t

• b.    Crossover – using multipoint crossover method generate intermediate main population O_m

• c.    Mutation – flip bit mutation is used to add population diversity to O_m

Step IV: Inbreeding of reserve population

• a.    Selection – using tournament selection select best fit parents from R t

• b.    Crossover – using multipoint crossover method generate intermediate reserve population O r

• c.    Mutation – flip bit mutation is used to add population diversity to O r

Step V: Crossbreeding

• a.    Offspring C of size (n-m) using best individuals from O m and O r

• b.    Make I m = C U O m and I r = C U O r

Step VI: Decoding: Decode both population using IEEE 754 algorithm from binary value representation to decimal value representation

Step VII: Evaluation

• a.  Evaluate I_m using fm(x)

• b.  Evaluate I r using fr(x)

Step VIII: Survival selection from Im of size m and from Ir of size n t = t + 1

Until fm(x) > = global optimal value or t > tmax

End

Where, t : index of current generation               M0, R0: main, reserve population fm(x): objective function                   Om, Or: intermediate main, reserve population respectively fr(x): fitness function for reserve population Im, Ir: constitute set of main, reserve population respectively —

• Fig. 2. Pseudo code of DPGA_MCSM

  Table I describes ten functions from CEC 2006 that we have implemented using DPGA_MCSM. It describes function name, dimension (D), type of function, no. of linear inequality constrains (LI), no. of non-linear inequality constrains (NI), no. of linear equality constrains (LE) and no. of non-linear equality constrains (NE).

Table II describes the parameter settings used for experimentation. Above parameter values are used for all functions. Consecutive 30 runs are taken for each function these parameter values. Size of main population is taken 100 where the size of reserve population size is taken 200. Crossover rate, elitism rate, mutation rate and crossbreed rate are kept same for both the main population and the reserve population.

Table III exhibits the optimal values found for the some functions using Ant Bee Colony Algorithm (ABC), Differential Evaluation (DE), and Genetic Algorithm (GA). ABC, DE, GA find exact optimum solution in 2, 40,000 function evaluations [37] where DPGA_MCSM gives solution close to optimal value in just 10, 000 average function evaluations.

Table IV shows statistical results obtained by DPGA _MCSM algorithm for 9 test functions from CEC 2006

over 30 independent runs using average 10,000 function evaluations. It contains function name, global optimum value, best value, mean value and worst value, standard deviation (S.D.) and standard error of mean (S.E.M.) obtained in 30 independent runs.

Table 1. Function Description

Functi-on	D	Type	LI	NI	LE	NE
g01	13	Quadratic	9	0	0	0
g02	20	Nonlinear	0	2	0	0
g04	5	Quadratic	0	6	0	0
g06	2	Cubic	0	2	0	0
g07	10	Quadratic	3	5	0	0
g08	2	Nonlinear	0	2	0	0
g09	7	Polynomial	0	4	0	0
g10	8	Linear	3	3	0	0
g18	9	Quadratic	0	13	0	0
g24	2	Linear	0	2	0	0

Table 3. Optimal solutions for other algorithms

Function	GA [20]	DE [20]	ABC [20]
g01	-14.23	-14.55	-15.00
g04	-30590.45	-30665.54	-30665.53
g06	-6872.20	–	-6961.81
g07	34.98	24.31	24.47
g08	0.096	0.096	0.095
g09	692.06	680.63	680.64
g10	10003.22	7147.33	7224.40

Table 4. Results of DPGA_MCSM for consecutive 30 runs

Function	Global	Best	Mean	Worst	S.D.	S.E.M
g01	-15.00	-15.00000	-10.87479	-7.71976	1.58263	0.28895
g04	-30665.538671	-30649.49587	-30490.11261	-30234.17525	108.74284	19.85364
g06	-6961.813875	-6960.15972	-6691.46685	-6352.67120	142.49572	26.01604
g07	24.306209	74.522052	127.71353	194.30380	30.64218	5.594
g08	-0.095825	-0.094837	-0.08918	-0.07323	0.00459	0.00084
g09	680.630057	677.228267	663.23351	602.43395	16.99565	3.10297
g10	7049.24802	7013.121872	5876.105700	4667.755859	566.19879	103.37328
g18	-0.866025	-0.835853	-0.759260	-0.622790	0.05414	0.00989
g24	-5.508013	-5.508018	-5.430250	-5.372550	0.06961	0.01271

In order to analyze on which specific kind of problem, the DPGA_MCSM algorithm performs better or not, the results should be examined. DPGA_MCSM cannot find solution to the problems having equality constrains. It gives best solution almost equal to global optimum value for g01, g06 and g24 whereas algorithm gives best solution close to global optimum value for g04, g08, g09, g10 and g18. DPGA_MCSM cannot optimize g07.

V. Conclusion

This paper proposes a novel technique for solving COPs using DPGA. The DPGA_MCMS algorithm initializes individuals satisfying all constrains. DPGA meta-heuristic is applied on these individuals and then several generations of DPGA optimize the objective function. This algorithm can solve problems that have only inequality constrains. Though the DPGA_MCMS algorithm fails to produce exact global optimal value, it succeeds in finding optimal solutions closer to global optima.

Though the DPGA_MCMS algorithm slightly deviates from global optima in future different constrains handling technique can effectively solve COPs using DPGA.

Appendix A.

g01: Minimize 4          4         13

f (х) = 5    — 5^х,2 — ^"х, i=l        i=l      i=5

Subject to дг (x) = 2x4 + 2x2 + 2x10 + 2xn —10 < 0

д_г (x) = 2x₄ + 2x₂ + 2x₁₀ + 2x_u — 10 < 0

y₂ ® ⁼ 2x₄ + 2x₃ + 2x₁₀ + 2x₁₂ — 10 < 0

g₃ CO ⁼ 2x₂ + 2x₃ + 2x_u + 2x₁₂ — 10 < 0

S₄(O = -8x₁ + x₁₀< 0

55 (О = -8x2+xn < 0

5₆(0 = -8x₃+x₁₂ < 0

y7(O = 2x4-x5+x10< 0

58(0 = 2x6-x7+xn< 0

y9(x) = 2xg-x9 + x12<0

where the bounds are 0 <= xi <= 1 (i=1,……,9), 0 <= xi <= 100 (i = 10, 11, 12) and 0 <= x13<=1 .

g04: Minimize f (x) = 5.3578547xf + 0.8356891%! + Xs + 37.293239xt -40792.141

Subject to

Si (x) = 85.334407 + 0.0056858x2xs + 0.0006262x1x4

Table 2. Parameter Settings

Crossover Rate	0.80	Elitism Rate	0.20
Mutation Rate	0.09	Crossbreed Rate	0.10
Main Pop. Size	100	Reserve Pop. Size	200

+ 0.0022053х3х5 - 92 < О

У2(О = -85. .334407хх - 0.0056858х2Х5

-0.0006262x^4 + 0.0022053х_эх₅ < О

53(х) = 80.51249 + 0.0071317х2х5 + 0.0029955х1х2

—0.0021813х3 - 110 < О у4(х) = -80.51249 - 0.0071317х2х5 - 0.0029955хгх2 — 0.0021813х3 + 90 < О

55(х) = 9.300961 + 0.0047026х3х5 + 0.0012547х1х3

+ 0.0019085хэх4 - 25 < О у6(х) = -9.300961 - 0.0047026х3х5 - 0.0012547х1х3 — 0.0019085хэх4 + 20 < О where 78 <= x1<= 102, 33 <= x2<= 45 and 27 <= xi<=

45 (i = 3, 4, 5).

д3(х) = -1 + 0.01(х8 - х5) < О у4(х) = -хгх6 + 833.33252х4 + 100хг - 83333.333 < О 5s(х) = —Х2Х7 + 1250х5 + х2х4 — 1250х4 < О

Уб (О = -хзхв + 1250000 + х3х5 - 2500х5 < О where 100 <= x1<= 10000, 1000 <= xi<= 10000 (i =

2,3) and 10 <= x i <= 1000 (i = 4,…,8).

g06: Minimize

/(х) = (х3 - 10)3 + (х2 - 20)3

Subject to

51(0 = -Сч - 5)2 - (х2 - 5)2 + 100 < О

5г(0 = Ui - 6)² + (х₂ - 5)² - 82.81 < О where 13 <= x1<= 100 and 0 <= x2<= 100.

g07: Minimize f (О = х? + х? + х4х7 — 14xt — 16х7 + (х, — 10)2 +4(х4 - 5)2 + (х5 - З)2 + 2(х6 - I)2 + 5х2

+7(х8 - 11) 2 + 2(х9 - 10)2 + (х10 - 7)2 + 45 Subject to дг (О = —105 + 4xt + 5х2 — Зх7 4- 9х8 < О 52(0 = 10х3 — 8х2 — 17х7 + 2х8 < О д3 (О = —8xt + 2х2 + 5хд — 2х10 —12 < О у4(0 = З(х3 - 2)2 + 4(х2 - З)2 + 2x1 - 7х4 — 120 < О д5(О = 5х2 + 8х2 + (х3 — 6)2 — 2х4 — 40 < О Эв® = х2 + 2(х2 — 2)2 — 2х3хг + 14х5 — 6х6 < О у7(0 = 0.5(х7 — 8)2 + 2(х2 — 4)2 + Зх; — х6 — 30 < О 5s(0 = —Зх2 + 6х2 + 12(х9 — 8)2 — 7х10 < О where -10 <= xi<= 10 (i = 1,…., 10).

g18: Minimize

f(x) = -О 5 fX1 Х4~ Х2 хз + хз ^9 - )

V Xq Xq -|- Xq Xr — Ха X7 '

Subject to ggl (x) = x2 + x2 — 1 < 0

99б (X) = (xi - x7)2 + (x2 - xB)2 - 1 <0

997 (О = (^3 ~ x5)2 + (x4 - x6)2 - 1 <0

99b (0 = (x3 - x7)2 + (x4 - x8)2 - 1 <0

ggs (x) = x2 + (xa - x9)2 - 1 <0

99io (x) = x₂ x₃ - Xi x₄< 0

99u(x) = -x₃x₉<  0

УУ12 (%) = x₅ x₉< 0

5513 (0 = x₆x₇ - x₅x₈< 0

where the bounds are - 10 ≤ xi ≤ 10 ( i = 1 , . . . , 8) and

0 ≤ x 9 ≤ 20.

g24: Minimize

f(x)= -х_г- x₂

Subject to

5i (O = -2x3 + 8x2 - 8x2 + x2 — 2 < 0

5z(O = ~4Xi + 32x2 ~ 88x2 + 96хг + x2 - 36 < 0

where the bounds are 0 <= x1<= 3 and 0 <= x2<= 4.

g08: Minimize

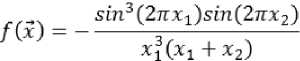
Acknowledgment

We express our sincere thanks to the all authors, whose papers in the area of DPGA and COPs are published in various conference proceedings and journals. Our special thanks to T. Park, R. Choe and K.R. Ryu for their work on Dual Population Genetic Algorithm published in various journals and conferences.

Subject to

5i(O= xf-x2 + 1 < О y2(O = l-Xi + (x2-4)2 <0

where 0 <= x1<=10 and 0 <= x2<= 10.

g09: Minimize

/ХО = (xj - 10)² + 5(х₂ - 12)² + х^ + 3(х₄ - II)² +Х;— 4х₆х₇ — 10х₆— 8х₇

Subject to

51(0 = -127 + 2х² + Зх₂ + х₃ + 4х₄ + 5x_s< О д₂ (х) = -282 + 7х_г + Зх₂ + 10х₃ + х₄ - х₅< О у₃(х) = -196 + 23х_г + Х₂ + 6x1 — 8х₇ < О у₄(х) = 4х? + х₂ — Зх,х₂ + 2х₃ + 5х₆ — 11х₇< О where- 10 <= xi<= 10 for (i = 1,….., 7).

g10: Minimize

f(x)= х₁ + х₂ + х_э

Subject to дг(х) = -1 + 0.0025(х4 + х6) < О д2(х) = -1 + 0.0025 (х5 + х7 - х4) < О