Два быстрых метода нахождения наибольшего общего делителя
Автор: Амер Исмаил Фалах Омар, Аль Халиди Аркан Мохаммед Али
Рубрика: Информатика и вычислительная техника
Статья в выпуске: 1, 2021 года.
Бесплатный доступ
Рассмотрены новые высокопроизводительные алгоритмы нахождения наибольшего общего делителя (НОД), разработанные на основе вавилонской системы исчисления и базиса Крестенсона. Произведены оценки вычислительной сложности основных операций усовершенствованного алгоритма поиска НОД в базисе Крестенсона. Представлены результаты сравнительного анализа усовершенствованного алгоритма поиска НОД в базисе Крестенсона со стандартным алгоритмом Евклида в вавилонской системе счисления и алгоритмом поиска НОД с помощью базиса Крестенсона.
Наибольший общий делитель, теория чисел, алгоритм евклида, вычислительная сложность, метод нахождения
Короткий адрес: https://sciup.org/148321541
IDR: 148321541 | УДК: 681.3 | DOI: 10.25586/RNU.V9187.21.01.P.150
Текст научной статьи Два быстрых метода нахождения наибольшего общего делителя
Актуальность работы
Наиболее распространенным методом нахождения НОД является один из древнейших математических алгоритмов – алгоритм Евклида, согласно которому для нахождения НОД двух чисел необходимо несколько раз от большего числа отнять меньшее, пока разница не станет меньше вычитателя [8–10]. Тогда эту же самую процедуру требуется выполнить с вычитаемым и разностью. Процесс вычитания будет продолжаться до тех пор, пока вычитаемое и разность не станут одинаковы. Поскольку числа, над которыми выполняются операции, на каждом шаге уменьшаются, то такой процесс не может продолжаться бесконечно, а закончится через некоторое число шагов [2–5].
Современная математическая запись алгоритма Евклида имеет следующий вид [1, 6, 7]: для любого a > b = r 0, где a и b – целые числа, выполняется система уравнений
Два быстрых метода нахождения наибольшего общего делителя a = r0 × q1 + r1, 0 ≤ r1 < r0; r0 = r1 × q2 + r2, 0 ≤ r2 < r1 r0 = r1 × q2 + r2, 0 ≤ r2 < r1
rn –2 = rn –1 × qn + rn , 0≤ rn < rn –1; rn –1 = rn × qn +1 + 0.
НОД ( а , b ) равен rn , то есть последнему ненулевому члену последовательности ri . Поскольку r 0 > r 1 > r 2… > rn >0, то данный процесс закончится минимум через b шагов, то есть нужно выполнить b делений с остатком. Однако данная оценка является неудовлетворительной, поскольку для нахождения НОД двух чисел (или проверки на простоту), которые используются в современных асимметричных криптосистемах, требуется очень большой объем времени. В [8] показано, что для нахождения НОД с помощью алгоритма Евклида нужно выполнить не более чем 5 k операций деления с остатком, где k – количество цифр в десятичной записи числа а . В [9] показано, что количество шагов не превышает 2log2 b + 1. Иная оценка следует из теоремы Ламе [10], согласно которой количество шагов алгоритма Евклида не превышает ^ 1од ф (л/5 a ) J -2, где [ a ] - верхнее целое a ; Ф = (1 + Vs)/2 - больший корень характеристического уравнения последовательности Фибоначчи.
Несмотря на указанные оценки и простоту программной реализации алгоритма Евклида, его вычислительная сложность остается большой, так как операция деления является достаточно трудоемкой. Расчеты показывают, что поиск НОД с использованием алгоритма Евклида в базисе Радемахера [8] характеризуется вычислительной сложностью по меньшей мере 17,5 × n ( n + 1)2, где n – разрядность числа а в двоичном коде.
Другим недостатком алгоритма Евклида является последовательное выполнение операции деления одна за другой, то есть невозможность его распараллеливания.
Перспективным направлением совершенствования исследуемых алгоритмов является разработка теории их реализации на основе вавилонской системы счисления остаточных классов.
Цель работы
Разработать новые высокопроизводительные алгоритмы нахождения НОД с помощью вавилонской системы исчисления и базиса Крестенсона, которые характеризуются значительно меньшей вычислительной сложностью, чем стандартный алгоритм Евклида.
Алгоритм Евклида в вавилонской системе счисления. Пусть требуется найти НОД чисел а и b :
a = an –12 n –1 +...+ ai 2 i +...+ a 1 2 + a 0;
b = bn–12n–1 +...+ bi2i +...+ b12 + b0, причем a > b = r0; a,b = 0,1.
Исходя из (1)
r 1 = a mod b = ( a ( n - 1 ) f n — 1
2 ( n 1 ) + ... + a . 21 + ... + a 1 2 + a 0 )mod b = n — 1\
= ^ ( a i 2 i mod b ) mod b = ^ ( a i r i ) mod b ,
k i = 0
k i = 0
где r 1 i = 2 i mod b .
Анализ данных и интеллектуальные системы
Это означает, что искомый остаток будет равен сумме трех степеней двойки, для которых аі = 1.
Следует отметить также, что два последовательных значения – r 1 i и r 1 i +1 – связаны рекуррентным соотношением r 1 i +1 = (2 × r 1 i )mod b .
Для нахождения остатка по модулю b необязательно выполнять деление с остатком, а можно ограничиться вычитанием: если r 1 i +1< b , то оно остается неизменным, в противном случае r 1 i +1 = r 1 i +1 – b . Проще всего реализовать описанный шаг алгоритма Евклида в вавилонской системе счисления с помощью таблицы 1.
Таблица 1
Нахождение остатка a mod b
|
a n –1 |
an –2 |
a i |
a 2 |
a 1 |
a 0 |
||
|
r 1 n –1 |
r 1 n –2 |
r 1 i |
r 12 |
r 11 |
r 10 |
В соответствии с таблицей 1 r 1 ищем как сумму r 1 i по модулю b , над которыми в верхней строке размещена 1, то есть r 1 = (^ , Q r 1 i ) mod b при условии a. = 1.
Аналогично строим таблицу 2.
Таблица 2
Нахождение остатка b mod r 1
|
b n –1= r 0 n –1 |
b n –2= r 0 n –2 |
b i = r 0 i |
b 2= r 0 2 |
b 1= r 0 1 |
b 0= r 0 0 |
||
|
r 2 n –1 |
r 2 n –2 |
r 2 i |
r 22 |
r 21 |
r 20 |
Соответственно, r 2 = ( ^ ,_0 r 2 i ) mod r 1 при условии b i = 1.
Обобщая полученные результаты, запишем выражение для нахождения любой
( n - 1 ^
modr j-1
Г = /Г rT-j I Z—i j- 2 i ji
V i = 1 2
где rj –2 i = 0,1; rji = 2 imj = modri –1.
Отметим, что количество шагов стандартного алгоритма Евклида и алгоритма Евклида в вавилонской системе счисления одинаковое. Однако вычислительная сложность выполнения каждого шага существенно уменьшается и составляет log2 n . Общая вычислительная сложность алгоритма Евклида в вавилонской системе счисления оценивается выражением O(17,5 n (log2 n )). Кроме того, он исключает возможность распараллеливания.
Алгоритм поиска НОД с помощью базиса Крестенсона
Предложен алгоритм нахождения НОД, основанный на поиске остатков от деления чисел а и b ( а > b ) в вавилонской системе счисления (2), (3) на все простые числа b .
Общим делителем чисел а и b будет модуль pjk , который находим из условия
(E: aj )mod pk=(E:—bn) mod pk=°, где aij = ai × 2imod pkj; bij = bi × 2imodpkj; pj – простое число, меньшее b; k = 1, 2, 3, ... – степень pj.
Два быстрых метода нахождения наибольшего общего делителя
Следует отметить, что при k = 1 и выполнении (4) проверяется условие при k = 2, и так далее. Таким образом, учитывается общий делитель, который является степенью простого числа. Искомый наибольший общий делитель находим как произведение полученных с помощью (4) общих делителей.
Предложенный алгоритм характеризуется логарифмической вычислительной
О( m × log2 n ),
dt
где m = J количество простых чисел в диапазоне от 2 до сложностью V b .
Кром2е того, он позволяет распараллелить выполнение всех операций по каждому модулю и выполнить факторизацию чисел а и b .
Усовершенствованный алгоритм поиска НОД с помощью базиса Крестенсона.
Предложенный выше алгоритм можно существенно усовершенствовать путем сокращения количества модулей (то есть количества шагов), по которым нужно искать остатки. Пусть имеем систему модулей, которая состоит из простых чисел р 1, р 2, р 3, ..., меньших b , и для некоторого pkj выполняется условие (4). Следующий шаг заключается в последовательной проверке условия (4) для модуля ( pkj pkj +1), k 1= 1, 2, 3,...; i = 1, 2, ...
Таким образом, при последовательном умножении модулей получаем, что
НОД ( a , b ) = ^Пн p kk , для которых выполняется условие (4).
По сравнению с предыдущим данный алгоритм использует меньшее количество шагов, однако он не поддается распараллеливанию и не решает задачу факторизации чисел.
Примеры применения алгоритмов поиска НОД. Пусть нужно вычислить НОД (3843, 1449).
1. Стандартный алгоритм Евклида: 3843 = 1449∙1+945
1449 = 945∙1+504
945 = 504∙1+441
504 = 441∙1+63
441 = 63∙7+0.
Следовательно, НОД (3843, 1449) = 63.
Алгоритм Евклида в вавилонской системе счисления
Данный алгоритм удобно представить в виде таблицы 3.
Таблица 3
Алгоритм Евклида в вавилонской системе счисления
|
1 |
3843 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
|
2 |
2 і mod1449 |
599 |
1024 |
512 |
256 |
128 |
64 |
32 |
16 |
8 |
4 |
2 |
1 |
|
3 |
1449 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
|
|
4 |
2 і mod945 |
79 |
512 |
256 |
128 |
64 |
32 |
16 |
8 |
4 |
2 |
1 |
|
|
5 |
945 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
||
|
6 |
2 і mod504 |
8 |
256 |
128 |
64 |
32 |
16 |
8 |
4 |
2 |
1 |
||
|
7 |
504 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
|||
|
8 |
2 і mod441 |
256 |
128 |
64 |
32 |
16 |
8 |
4 |
2 |
1 |
|||
|
9 |
441 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
|||
|
10 |
2 і mod63 |
4 |
2 |
1 |
32 |
16 |
8 |
4 |
2 |
1 |
Анализ данных и интеллектуальные системы
Строка 2: (599+1024+512+256+2+1)mod1449 = 945.
Строка 4: (79+256+128+32+8+1)mod945 = 504.
Строка 6: (8+256+128+32+16+1)mod504 = 441.
Строка 8: (256+128+64+32+16+8)mod441 = 63.
Строка 10: (4+2+32+16+8+1)mod63 = 0.
Таким образом можно получить НОД, избежав громоздкой операции деления.
Поиск НОД в базисе Кр естен сона. Данную задачу также удобно представить в виде таблицы 4, учитывая, что J 14449 ≈ 38.
Таблица 4
Нахождение остатков за простыми модулями
|
1 |
2048 |
1024 |
512 |
256 |
128 |
64 |
32 |
16 |
8 |
4 |
2 |
1 |
|
|
2 |
3843 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
|
3 |
1449 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
|
|
4 |
2 і mod2 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
5 |
2 і mod3 |
2 |
1 |
2 |
1 |
2 |
1 |
2 |
1 |
2 |
1 |
2 |
1 |
|
6 |
2 і mod5 |
3 |
4 |
2 |
1 |
3 |
4 |
2 |
1 |
3 |
4 |
2 |
1 |
|
7 |
2 і mod7 |
4 |
2 |
1 |
4 |
2 |
1 |
4 |
2 |
1 |
4 |
2 |
1 |
|
8 |
2 і mod11 |
2 |
1 |
6 |
3 |
7 |
9 |
10 |
5 |
8 |
4 |
2 |
1 |
|
9 |
2 і mod13 |
7 |
10 |
5 |
9 |
11 |
12 |
6 |
3 |
8 |
4 |
2 |
1 |
|
10 |
2 і mod17 |
8 |
4 |
2 |
1 |
9 |
13 |
15 |
16 |
8 |
4 |
2 |
1 |
|
11 |
2 і mod19 |
15 |
17 |
18 |
9 |
14 |
7 |
13 |
16 |
8 |
4 |
2 |
1 |
|
12 |
2 і mod23 |
1 |
12 |
6 |
3 |
13 |
18 |
9 |
16 |
8 |
4 |
2 |
1 |
|
13 |
2 і mod29 |
18 |
9 |
19 |
24 |
12 |
6 |
3 |
16 |
8 |
4 |
2 |
1 |
|
14 |
2 і mod31 |
2 |
1 |
16 |
8 |
4 |
2 |
1 |
16 |
8 |
4 |
2 |
1 |
|
15 |
2 і mod37 |
13 |
25 |
31 |
34 |
17 |
27 |
32 |
16 |
8 |
4 |
2 |
1 |
|
16 |
2 і mod9 |
5 |
7 |
8 |
4 |
2 |
1 |
5 |
7 |
8 |
4 |
2 |
1 |
|
17 |
2 і mod27 |
23 |
25 |
26 |
13 |
20 |
10 |
5 |
16 |
8 |
4 |
2 |
1 |
Из таблицы 4 ищем остатки за простыми модулями.
Строка 4: 3843mod2 = 1; 1449mod2 = 1.
Строка 5: 3843mod3 = (2+1+2+1+2+1)mod3 = 0;
1449mod3 = (1+1+2+2+2+1)mod3 = 0.
Строка 6: 3843mod5 = (3+4+2+1+2+1)mod5 = 3;
1449mod5 = (4+1+3+2+3+1)mod5 = 4.
Строка 7: 3843mod7 = (4+2+1+4+2+1)mod7 = 0;
1449mod7 = (2+4+2+4+1+1)mod7 = 0.
Строка 8: 3843mod1 = (2+1+6+3+2+1)mod11 = 4;
1449mod11 = (1+3+7+10+8+1)mod11 = 8.
Строка 9: 3843mod13 = (7+10+5+9+2+1)mod13 = 8;
1449mod13 = (10+9+11+6+8+1)mod13 = 6.
Строка 10: 3843mod17 = (8+4+2+1+2+1)mod17 = 1; 1449mod17 = (4+1+9+15+8+1)mod17 = 4.
Два быстрых метода нахождения наибольшего общего делителя
Строка 11: 3843 mod19 = (15+17+18+9+2+1)mod19 = 5;
1449mod19 = (17+9+14+13+8+1)mod19 = 5.
Строка 12: 384mod23 = (1+12+6+3+2+1)mod23 = 2;
1449mod23 = (12+3+13+9+8+1)mod23 = 0.
Строка 13: 3843mod29 = (18+9+19+24+2+1)mod29 = 15;
1449mod29 = (9+24+12+3+8+1)mod29 = 28.
Строка 14: 3843mod31 = (2+1+16+8+2+1)mod31 = 30;
1449mod31 = (1+8+4+1+8+1)mod31 = 23.
Строка 15: 3843mod37 = (13+25+31+34+2+1)mod37 = 32;
1449mod37 = (25+34+17+32+8+1)mod37 = 6.
Данные расчеты показывают, что общими простыми делителями являются числа 3 и 7. Для нахождения НОД нужно проверить их степени:
Строка 16:
3843mod32= (5+7+8+4+2+1)mod32= 0; 1449mod32 = (7+4+2+5+8+1)mod32= 0.
Строка 17:
3843mod33= (23+25+26+13+2+1)mod33= 9;
1449mod33= (25+13+20+5+8+1)mod33= 18.
Число 72 = 49 > 38, и его можно не проверять.
Следовательно, НОД (3843, 1449) = 32 ⋅ 7 = 63. Данный метод позволяет провести факторизацию чисел, например, 1449 = 32 ⋅ 7 ⋅ 23. Кроме того, вычисления можно выполнять параллельно с различными модулями.
Усовершенствованный алгоритм поиска НОД в базисе Крестенсона
Строим таблицу 5.
Таблица 5
Нахождение остатков в усовершенствованном алгоритме
|
1 |
2048 |
1024 |
512 |
256 |
128 |
64 |
32 |
16 |
8 |
4 |
2 |
1 |
|
|
2 |
3843 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
|
3 |
1449 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
|
|
4 |
2 і mod2 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
5 |
2 і mod3 |
2 |
1 |
2 |
1 |
2 |
1 |
2 |
1 |
2 |
1 |
2 |
1 |
|
6 |
2 і mod9 |
5 |
7 |
8 |
4 |
2 |
1 |
5 |
7 |
8 |
4 |
2 |
1 |
|
7 |
2 і mod27 |
23 |
25 |
26 |
13 |
20 |
10 |
5 |
16 |
8 |
4 |
2 |
1 |
|
8 |
2 і mod45 |
23 |
34 |
17 |
31 |
38 |
19 |
32 |
16 |
8 |
4 |
2 |
1 |
|
9 |
2 і mod63 |
32 |
16 |
8 |
4 |
2 |
1 |
32 |
16 |
8 |
4 |
2 |
1 |
|
10 |
2 і mod441 |
284 |
142 |
71 |
256 |
128 |
64 |
32 |
16 |
8 |
4 |
2 |
1 |
|
11 |
2 і mod693 |
662 |
331 |
512 |
256 |
128 |
64 |
32 |
16 |
8 |
4 |
2 |
1 |
Анализируем таблицу 5.
Строка 4: 3843mod2 = 1; 1449mod2 = 1.
Строка 5: 3843mod3 = (2+1+2+1+2+1)mod3 = 0;
1449mod3 = (1+1+2+2+2+1)mod3 = 0.
Анализ данных и интеллектуальные системы
Строка 6: 3843mod9 = (5+7+8+4+2+1)mod9 = 0;
1449mod9 = (7+4+2+5+8+1)mod9 = 0.
Строка 7: 3843mod27 = (23+25+26+13+2+1)mod27 = 9;
1449mod27 = (25+13+20+5+8+1)mod27 = 18.
Строка 8: 3843mod45 = (23+34+17+31+2+1)mod45 = 18;
1449mod45 = (34+31+38+32+8+1)mod45 = 9.
Строка 9: 3843mod63 = (32+16+8+4+2+1)mod63 = 0;
1449mod63 = (16+4+2+32+8+1)mod63 = 0.
Строка 10: 3843mod441 = (284+142+71+256+2+1)mod441 = 315;
1449mod441 = (142+256+128+32+8+1)mod441 = 126.
Строка 11: 3843mod693 = (662+331+512+256+2+1)mod693 = 378;
449mod693 = (331+256+128+32+8+1)mod693 = 63.
Из расчетов также следует, что НОД (3843, 1449) = 63.
Кроме того, отметим, что в двух последних алгоритмах необязательно искать остатки от обоих чисел а и b . Достаточно найти остатки от меньшего числа и только при их равенстве 0 проверять второе число.
Оценка вычислительной сложности известного и предложенных алгоритмов поиска НОД. Сложность предложенных алгоритмов определяется вычислительной сложно- стью следующих операций:
-
1) нахождение остатков aj , bj чисел X , Y по простым модулям pmji , для которых выполняется условие aj = bj = 0;
-
2) вычисление произведения модулей Z = НОД ( X , Y ) = П ■ , P m •
В таблице 6 приведены оценки вычислительной сложности основных операций алго- ритма поиска НОД в базисе Крестенсона, что позволяет сделать сравнительный анализ с приведенными выше алгоритмами поиска наибольшего общего делителя.
Таблица 6
Вычислительная сложность основных операций алгоритма поиска НОД в базисе Крестенсона и его совершенствование
|
№ п/п |
Основные операции |
Вычислительная сложность |
|
1 |
p mj |
z-x I _L . n )) O l log 2 n xl log 2 n +— I I |
|
2 |
n — 1 _ ( m) _ _ 1 X ' _ / _ _ J . m X 1 a j = res l / < a^ (mod p j ) 1 , V i = 1 ) aT ) = res | £ ^(mod p m ) | V i = 1 ) |
( n I O l log2 n +—I |
|
3 |
k Z = П Pm- j = 1 |
0( k × log2 n ) |
|
k – количество модулей, для которых выполняется условие aj = bj = 0. |
||
С учетом данных таблицы 6 общая вычислительная сложность предложенного алгоритма поиска НОД в базисе Крестенсона и его усовершенствования будет определяться суммой сложностей основных операций, соответственно,
Два быстрых метода нахождения наибольшего общего делителя
~ I n
O l lOg2 n Xl lOg2 n + 2
( n\n,n ^
O3 l l0g 2 n l l0g 2 n + k X l0g 2 n + ^ 1 + 2log 2 2 I "
На рисунке изображены графики, которые характеризуют сложности существующего и предложенных алгоритмов в зависимости от разрядности компонентов Z .
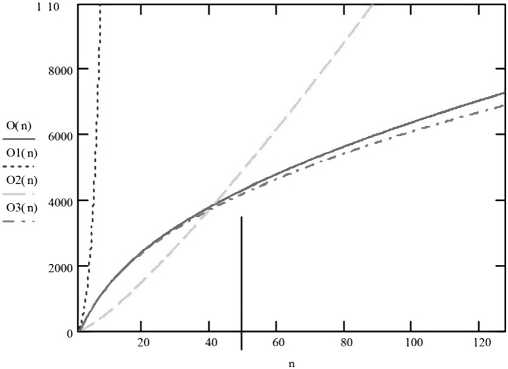
Сложности алгоритмов поиска НОД( X , Y ):
O( n ) – в базисе Крестенсона; O1( n ) – алгоритма Евклида;
O2( n ) – совершенствование реализации алгоритма Евклида с использованием вавилонской системы счисления;
O3( n ) – усовершенствованный алгоритм поиска НОД в базисе Крестенсона
Численный эксперимент оценки сложности предложенных алгоритмов поиска НОД показывает, что в диапазоне двоичных разрядов от 0 до 42 бит следует использовать усовершенствования реализации алгоритма Евклида с использованием вавилонской системы счисления Радемахера – Крестенсона, а при увеличении разрядности чисел – алгоритм поиска НОД в базисе Крестенсона и его совершенствование.
Заключение
Предложенные теоретические основы поиска НОД с применением теоретико-числового базиса Крестенсона и вавилонской системы счисления остаточных классов позволяют уменьшить вычислительную сложность на 1–2 порядка, проводить вычисления с использованием параллельной технологии и эффективно использовать для реализации высокопроизводительных алгоритмов обработки и защиты информационных потоков на основе асимметричных алгоритмов шифрования.
Список литературы Два быстрых метода нахождения наибольшего общего делителя
- Амер И., Ишмухаметов Ш.Т. Об ускорении k-арного алгоритма вычисления НОД натуральных чисел // Ученые записки Казан. ун-та. Серия "Физико-математические науки". 2019. Т. 161, кн. 1. С. 110-118. DOI: 10.26907/2541-7746.2019.1.110-118
- Гашков С.Б., Сергеев И.С. Об аддитивной сложности матриц НОД и ОК // Математические заметки. 2016. Т. 100, № 2. С. 196-211.
- Корюкин А.Н., Себельдин А.М., Силла А.Л. Кольца с наибольшим общим делителем // Фундаментальная и прикладная математика. 2010. Т. 16, № 7. С. 69-74.
- Малашонок Н.А. НОД многочленов дуального переменного // Вестник Тамбовского ун-та. Серия "Естественные и технические науки". 2012. Т. 17, № 1. С. 91-92.
- Малашонок Н.А. Результант на алгебре дуальных чисел // Вестник Тамбовского ун-та. Серия "Естественные и технические науки". 2013. Т. 18, № 1. С. 110-111.
- Окулов С.М., Лялин А.В. Расширенный алгоритм Евклида // Информатика и образование. 2011. № 8. С. 37-41.
- Оленев А.А. Особенности реализации алгоритма Евклида в MAPLE // Актуальные вопросы инженерного образования - 2015: сборник науч. трудов Междунар. науч.-метод. конф. (Октябрьский, 27 ноября 2015 г.). Ставрополь: Альфа Принт, 2016. С. 160-167.
- Павлова Т.В., Токц Н.А. Применение теоремы о линейной форме наибольшего общего делителя к решению сравнений первой степени // Проблемы и перспективы физико-математического и технического образования: сборник материалов Всерос. науч.-практ. конф. / отв. ред. Т.С. Мамонтова. 2015. С. 158-164.
- Фалин Г., Фалин А. Избранные задачи на делимость целых чисел // Математика. Первое сентября. 2013. № 5. С. 43-50.
- Цирулик В.Г. Неевклидов алгоритм отыскания наибольших общих делителей систем многочленов // Научные труды SWorld. 2014. Т. 29, № 1. С. 89-91.


