Два подхода к построению моделей прогноза риска прогрессирующего атеросклероза



Ложкина Н.Г., Воскобойников Ю.Е., Копылов В.Н., Пархоменко О.М., Воевода М.И. Два подхода к построению моделей прогноза риска прогрессирующего атеросклероза. Сибирский журнал клинической и экспериментальной медицины. 2023;38(2):89–97.

Синдром быстро прогрессирующего или ускоренного атеросклероза, в отличие от спонтанного течения процесса, привлекает внимание исследователей в последние 2–3 десятилетия [1]. В его развитии помимо классических факторов риска играют роль и ряд других медиаторов: воспаления, кальцификации, остеопонтин [2]. Пациенты с быстропрогрессирующим атеросклерозом подвержены наибольшему риску развития различных ишемических событий, требующих постоянного медицинского внимания и специфической, более агрессивной липидснижаю-щей и антитромботической терапии [3].

Цель исследования: сравнить два подхода к созданию прогнозной модели риска прогрессирующего атеросклероза: метод нелинейной регрессионной модели логистического типа и метод свободной кроссплатформенной системы визуального программирования Orange.

Материал и методы

Исследование включало 202 пациента с ишемической болезнью сердца (ИБС): 147 мужчин и 55 женщин (ретроспективное когортное методом параллельных групп). Средний возраст пациентов составил 53,3 ± 7,16 лет. Диагноз ИБС был установлен в соответствии с набором критериев, разработанных Европейским обществом кардиологов и Американским колледжем кардиологов (2019, 2021) [4, 5]. Ретроспектива охватывала 2 года с момента включения пациентов в исследование (период с января 2019 по январь 2020 гг.) с определением 100 клинических, инструментальных, лабораторных параметров, которые потенциально влияют на возникновение и прогрессирование атеросклероза (по данным анализа литературы).

Данные обследования проводились и оценивались в 2 точках: во время 1-го предшествующего ишемического события в течение 2-летнего ретроспективного периода и в день включения в настоящее исследование.

202 пациента были разделены на 2 группы. В первую – активную (100 человек) включали пациентов, у которых был инфаркта миокарда (ИМ) 1-го типа [6] (54 человека) в течение 2 лет до начала исследования или диагноз ИБС был установлен по данным селективной коронарной ангиографии: наличие стеноза просвета как минимум двух коронарных артерий на 50% и более (46 человек) и которые имели дополнительно два (или более) сердечно-сосудистых события из следующих: ИМ или нестабильная стенокардия, экстренное артериальное стентирование, инсульт, тромбоз периферических артерий, критическая ишемия и ампутация нижних конечностей. Сочетание двух или более из этих сердечно-сосудистых событий, произошедших в течение 2 лет, указывает на быстрое прогрессирование атеросклероза у этих пациентов.

Данные клинические состояния свидетельствуют о нестабильном, или прогрессирующем, течении заболевания; это критерии так называемого «истинного прогрессирования», т. к. сахарный диабет и фибрилляция предсердий также могут привести к вышеперечисленным состояниям, но они имеют под собой несколько иную причину, не связанную с простым повреждением бляшки. Основным документом, пожалуй, следует считать рекомендации ESC/EAS по применению ингибиторов PCSK9 [7].

В других источниках прогрессирующий атеросклероз описан в категории экстремального сердечно-сосудистого риска. Наиболее подробный обзор по этой проблеме сделан P. Shah и соавт. (2015) [1]. Российские ученые М.В. Биленко и соавт. (2010), Т.И. Арефьева и соавт. (2015, 2016) обосновали 3 способа предсказания прогрессирующего атеросклероза, основанные на маркерах воспаления, концентрации Интерлейкин-10-продуцирующих Т-лимфоцитов, способности макрофагов а) продуцировать активные формы кислорода, оцененные по величине люминол-зависимой хемилюминесценции, б) окислять липопротеины низкой плотности (ЛПНП), оцененные по накоплению в них продуктов, реагирующих с тиобарбиту-ровой кислотой, в) поглощать ЛПНП, оцененные по накоплению в макрофагах общего холестерина и г) по сохранению 50–70% жизнеспособных макрофагов в процессе 1 ч инкубации в безбелковой субстрат-дефицитной среде [8–10]. Ю.И. Рагино в 2019 г. описала лабораторные и биохимические маркеры нестабильной атеросклеротической бляшки, играющей важную роль в возникновении повторных сердечно-сосудистых событий [11].

Вторая группа (группа сравнения) включала 102 пациента с подтвержденной ИБС аналогичным образом (55 человек имели в прошлом только один ИМ 1-го типа, а 45 – ИБС, подтвержденную селективной коронарной ангиографией соответственно), у которых за 2 года до включения в исследование не было сердечно-сосудистых событий, что свидетельствовало о так называемом спонтанном течении атеросклероза. Все пациенты прошли клиническое и инструментальное обследование по следующей программе: электрокардиография, эхокардиография, холтеровское мониторирование, исследование воспалительных цитокинов.

Существенной особенностью прогнозных моделей риска ускоренного развития атеросклероза является вычисление вероятности случайного события, которое заключается в ускоренном развитии атеросклероза. Следовательно, прогнозная модель вычисляет величину (вероятность), которая может меняться в интервале от 0 до 1. При этом если вероятность меньше некоторой пороговой величины, то делается вывод о низком риске, если равно или больше, то о высоком риске. Ниже будут изложены два подхода к построению прогнозных моделей ускоренного развития атеросклероза.

Первый подход содержит построение прогнозной модели на основе нелинейной регрессионной модели логистического типа. При построении регрессионных моделей, устанавливающих связь между переменными (факторами) исследуемого процесса используют понятия зависимой и независимых переменных. Под независимой переменной подразумевают некоторый фактор, воздействующий на другой наблюдаемый фактор, который будем называть зависимой переменной. В данном исследовании зависимой переменной (обозначим Y) является факт ускоренного развития атеросклероза. Примерами независимых переменных являются: привычка курения, наличие ожирения и т. д. Так как зависимая переменная Y принимает только два значения (1 – высокий риск атеросклероза, т. е. неблагоприятный исход (НИ), 0 – низкий риск, т. е. благоприятный исход (БИ)), поэтому для описания исследуемого процесса в качестве математической модели была принята регрессионная логистическая модель, вычисляющая вероятность неблагоприятного исхода.

В общем виде эта регрессионная модель описывается следующим выражением:

P ( X ) = _{1 +} ¹ _e – Z ( x ) , (1),

I где Z(X) = β0 + ∑   βj · Xj, βj, – неизвестные коэффи- j = 1

циенты регрессионной модели, X_j – независимые переменные (факторы) модели, M – количество переменных моделей. Видно, что значение P ( X ) может меняться от 0 (если Z ( X ) = – ꝏ) до 1 (при Z ( X ) = + ꝏ ), и поэтому P ( X )

можно интерпретировать как вероятность ускоренного развития атеросклероза.

При построении модели (1) будем решать следующие наиболее важные задачи:

– отбор наиболее информативных переменных X_j , которые значимо влияют на значение величины Z ( X ) и слабо коррелированы между собой;

– вычисление оценок bj для неизвестных коэффициентов βj, j = 0,1,.. M, и построение уравнения регрессии для оценивания вероятности ускоренного развития атеро- склероза в виде:

P ^ˆ( X )

1 + e

А ^;

f  М bo+Е bA

I      j - i

– проверка адекватности построенной модели (2) заданной выборке.

Из 100 изучаемых факторов были отобраны следующие 15, которые имели значимую корреляцию с зависимой переменной (исход сердечно-сосудистое событие) и слабую корреляцию этих независимых переменных между собой. Такими переменными оказались: возраст пациента – X1, пол пациента – X2, стеноз сонных арте- рий на 50% и более хотя бы на одной стороне – X3, артериальная гипертензия – X4, курение – X5, ожирение более 1 степени – X6, стабильная стенокардия в анамнезе – X7, уровень лейкоцитов в крови ЕД/л – X8, уровень креатинина крови – X9, уровень С-реактивного протеина в мг/л – X10, уровень общего холестерина крови в мМ/л – X11, уровень холестерина липопротеидов высокой плотности (ХС ЛПВП) в мМ/л – X12, уровень холестерина липопротеидов низкой плотности (ХС ЛПНП) в мМ/л – X13, фракция выброса левого желудочка в % – X14, многососудистое поражение коронарного русла – X15. Выборка из этих факторов объемом 202 использовалась дальше для построения логистической модели.

К сожалению, табличный процессор Excel не содержит встроенной функции, позволяющей построить логистическую регрессию. Поэтому нахождение оценок b_j для неизвестных коэффициентов β _j, j = 0,1,.. M , и вычисление точностных характеристик этих оценок осуществлялось с использованием модуля РЕГРЕССИЯ статистического пакета SPSS (версия 22), где такая возможность существует.

Для определения наиболее информативных независимых переменных в логистической регрессионной модели и вычисления коэффициентов при этих переменных использовался метод Вальда вперед, в котором построение начиналось с простейшей модели с одной независимой переменной, а затем вводилась на каждом шаге новая независимая переменная – наиболее информативная (т. е. максимально влияющая на значение величины Z ( X ) для данного шага. На рисунке 1 (скрин окна вывода пакета SPSS) приведены значения К_чув , К_спец , К_точ , характеризующие точность построенной модели на каждом шаге введения в модель новых переменных.

Таблица классификации3

		Предсказанные
	VAR00001		Процент
Наблюденные	.00	1.00	правильных
ШЗГ1 VAR00001   .00 1 00	75 0	100	73.5 100.0
			86.6
Шаг 2  VAR00001   .00 1,00	89 10	13 90	87,3 90.0
Общая процентная доля			88.6
Шаг3 VARQ0001 .00 1,00	92 6	10 94	90,2 94,0
Общая процентная доля			92.1
Шаг 4 VAR00001   .00 1,00	94 <	8 96	92.2 96.0
Общая процентная доля			94,1
Шаг 5 VAR00001   ,00 1,00	95 4	7 96	93.1 96.0
Общая процентная доля			94.6	‘ ^спеч
Шагб VAR00001   .00 1,00	96 3	6 97	94,1 * 97.0-
Общая процентная доля			95,5-
а Значение отсечения - .400

Рис. 1. Значения характеристик точности на каждом шаге построения уравнения регрессии Fig. 1. The values of the accuracy characteristics at each step of the regression equation

Расшифруем смысл этих коэффициентов:

– коэффициент чувствительности К_чув – оценка вероятности правильного прогноза НИ;

– коэффициент специфичности К_спец – оценка вероятности правильного прогноза БИ;

– коэффициент точности К_точ – оценка вероятности правильного прогноза как НИ, так и БИ.

Коэффициент К_точ является «суммарным» показателем точности прогноза построенной модели, и поэтому этот показатель дальше является определяющим при отборе переменных логистической модели.

Из рисунка 1 видно, что процедура добавления новых переменных в регрессионную модель заканчивается на шаге 6, когда значение коэффициента К_точ достигает максимального значения. На последнем шаге 6 мы имеем следующие значения коэффициентов:

Кчув = 94,1% (0,941), Кспец = 97,0% (0,97),

К_точ = 95,5% (0,955) , которые говорят о высоких точностных характеристиках модели.

На практике для вычисления этих коэффициентов используют следующую четырехпольную таблицу, учитывающую БИ и НИ (табл. 1).

Таблица 1. Четырехпольная таблица вычисления для коэффициентов чувствительности, специфичности и точности в построенное уравнение регрессии могут входить все 6 независимых переменных.

Таблица 2. Вычисленные коэффициенты b _j

Table 2. Calculated coefficients b ^j

Названия независимых переменных (факторов) Names of independent variables (factors)	Обозначения в логистической модели Designation in the logistical model	Коэффициенты b j Coefficients b j	Р-вели-чина P-level
Возраст Age	X 1	–0,766	0,000
Стеноз сонных артерий Stenosis of carotid arteries	X2	–3,119	0,008
Ожирение Obesity	X 3	–1,678	0,012
Стенокардия в анамнезе Angina in medical history	X4	4,016	0,000
СРБ CRP	Х 5	0,082	0,025
ЛПВП HDL	Х 6	–1,989	0,007
Константа Constant	b 0	47,581	0,000

Примечание: СРБ – С-реактивный белок, ЛПВП – липопротеины высокой плотности.

Note: CRP – C Reactive Protein, HDL – high density lipoproteins.

Table 1. Four-field table of calculations for sensitivity, specificity, and accuracy coefficient

Исходы Outcomes	Результат прогнозирования Prediction result		Итого Total
	Благоприятный исход – БИ (0) Favorable outcome – FO (0)	Неблагоприятный исход – НИ (1) Adverse outcome – AO (1)
Благоприятный исход (0) Favorable outcome	a – число больных с БИ и результат прогнозирования БИ a – the number of patients with FO and the result of FO prediction	b – число больных с БИ и результат прогнозирования НИ b – the number of patients with FO and the result of AO prediction	a + b – общее число больных с БИ a + b – the total number of patients with FO
Неблагоприятный исход (1) Adverse outcome	c – число больных с НИ и результат прогнозирования БИ c – the number of patients with AO and the result of FO prediction	d – число больных с НИ и результат прогнозирования НИ d – the number of patients with AO and the result of AO prediction	c + d – общее число больных с НИ c + d – the total number of patients with AO

Тогда коэффициенты вычисляются следующим обра зом:

К =   d , К   = a , К = a + d , чув   c + d , спец a + b , точ   a + b + c + d ,

В таблице 2 приведены названия независимых переменных, вошедших в регрессионную модель на шаге 6, обозначения этих переменных в регрессионной модели и значения вычисленных коэффициентов b_j . В последнем столбце таблицы 2 приведены так называемые Р-вели-чины. Если эта величина меньше или равна 0,05, то соответствующий вычисленный коэффициент b_j является значимым и переменная X_j может входить в построенное уравнение регрессии. Анализ таблицы 2 показывает, что все коэффициенты b_j, j = 0,1,.., 6 являются значимыми и

Подставляя вычисленные коэффициенты в уравнение (2), получаем конкретное уравнение логистической регрессии:

(X) =

1 + e – [47,581 – 0,7 66 X 1 – 3,119 X 2 – 1,6 78 X 3 + 4,016 X 4+ 0 ,0 8 2 X 5 – 1 , 9 8 9 X 6] ,

Очевидно, что для вычисления прогноза вероятности

(X) ускоренного развития атеросклероза у какого-либо пациента достаточно подставить в регрессию (4) значения его факторов (значения переменных, используемых в уравнении (4)). Прогнозное значение переменной Y (0 или 1) вычисляется по правилу:

Y = ^

0, если P(x ) <  0.4;

1, если P(x ) >  0.4,

(5),

где величина порога 0,4 найдена из условия максимума коэффициента точности К_точ .

Для упрощения использования построенной регрессионной модели формулы (4), (5) были реализованы в табличном процессоре Excel в виде специального калькулятора. Интерфейс калькулятора показан на рисунке 2. Данные пациента (значения переменных, приведенных в табл. 2) вводятся в ячейки, выделенные цветом.

Видно предельно простое использование этого калькулятора для прогноза риска ускоренного развития атеросклероза у конкретного пациента.

Второй подход к вычислению риска ускоренного развития атеросклероза существенно использует машинное обучение, представляющее альтернативный подход к моделированию прогнозов исходов, который может учесть нелинейные взаимосвязи [12]. Задача прогнозирования сводится к классификации пациентов на основе наиболее вероятных исходов. Машинное обучение – это один из методов искусственного интеллекта, решающий зада- чу не прямым способом, а путем поиска закономерностей в данных в результате обучения алгоритма на множестве примеров с известными исходами (БИ или НИ). При этом алгоритм обучается на наборе примеров, корректируется с помощью тестового набора, а уже потом применяется на реальных объектах (в данном случае – пациентах), нуждающихся в прогнозе. Другими словами, первый этап – это обучение, второй этап – прогноз.

1	8	СОЕ			F	G
	Обозначения переменных регрессионной модели	Обозначения коэффициентов регрессионной модели	Значения коэффициентов регрессионной модели
2 3 4 I 5 6 7		ЬО	47,581
	XI	ы	-0,766	порога	ол
	Х2	Ь2	-3,119
	хз	ЬЗ	-1,678	цх)	Вероятность Р(Х)	Y п редек
	Х4	Ь4	4,016	-4,808	0,01	0
	Х5	Ь5	0,082
8 9	Хб	Ь6	-1,989
10				Риск ускоренного развития атеросклероза НЕ ВЫСОКИЙ)
11
12 13 14 15 16		Введите значения переменных регрессионной модели (6 величин)
	XI	Х2	ХЗ	Х4	Х5	Х6
	Возраст	Стеноз сонных артерий	Ожирение	Стенокардия в анамнезе	СРВ	ЛПВП
	62	1	0	0	2,1	0,98

Рис. 2. Интерфейс калькулятора

Fig. 2. Calculator interface

Для решения поставленных задач использовалась свободная кроссплатформенная система визуального программирования Orange, разработанная Лабораторией биоинформатики Люблянского университета (Словения). Orange – инструмент с открытым исходным кодом для интеллектуального анализа данных, статистических исследований и визуализации данных, который обеспечивает визуальное программирование для построения рабочих процессов анализа. Пользовательский интерфейс системы легко осваивается специалистами из разных сфер, связанных с большими наборами разнообразных данных. На рисунке 3 показан рабочий процесс классификации объектов с помощью логистической регрессии, полученный визуальным программированием из модулей, называемых виджетами, которые реализуют отдельные алгоритмы и функции.

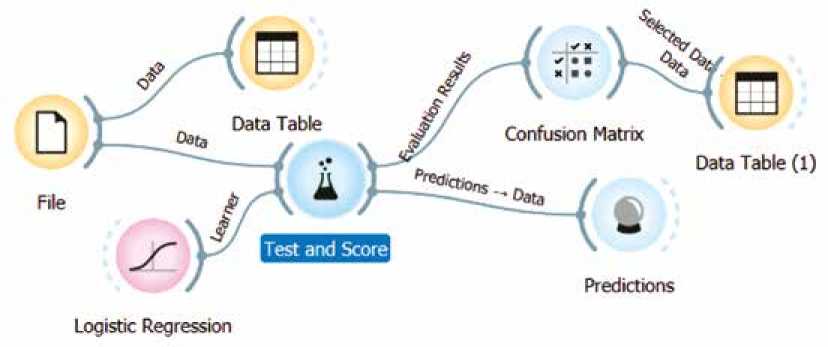
Data Table

Confusion Matrix

Data Table (1)

Predictions

Logistic Regression

Test and Score

Рис. 3. Рабочий процесс классификации объектов с помощью логистической регрессии Fig. 3. Workflow of object classification using logistic regression

Была проведена перекрестная проверка (crossvalidation) рассматриваемого алгоритма. В основном она используется в ситуациях, когда целью является прогнозирование, и требуется оценить, насколько точно прогностическая модель будет работать на практике. Исходный набор данных случайным образом делится на N равных частей. Сначала происходит обучение по N-1 частям, а тестирование – по N-й части. Затем тестовая часть меняется, и обучение проходит по оставшимся N-1 частям. Цикл состоит из N итераций, в ходе которых каждая часть будет использована в качестве тестовой. Результаты цикла обобщаются (усредняются). В качестве иллюстрации на рисунке 4 представлено окно перекрестной проверки алгоритма логистической регрессии при N = 3 и числе независимых переменных, равном 15. Коэффициент точности Кточ представлен как СА (classification accuracy) со значением 0,950 (95,0%).

Видно, что используя систему визуального программирования Orange, удается построить прогнозную модель такой же точности, что и в первом подходе (см. рис. 1). На рисунке 5 представлена четырехпольная таблица, называемая в системе Orange «матрицей разногласий» (аналог табл. 1) со значениями К_чув и К_спеец , при 15 независимых переменных.

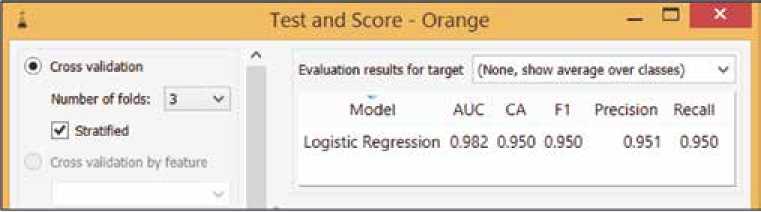
Рис. 4. Результат перекрестной проверки алгоритма логистической регрессии

Fig. 4. The result of cross-validation of the logistic regression algorithm

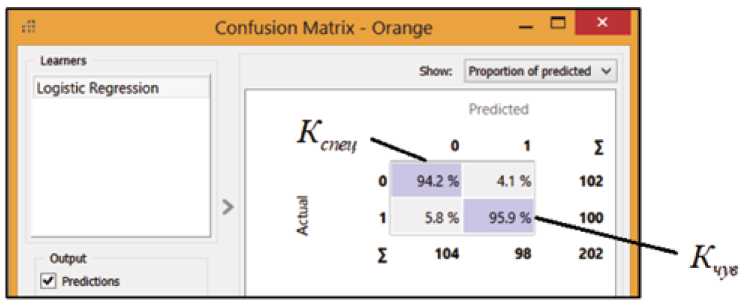
Рис. 5. Окно матрицы разногласий с коэффициентами К _чув , К _спеец Fig. 5. Disagreement matrix window with coefficients К _чув , К _спеец

Заметим, что в построенной регрессионной модели (4) использовались только 6 наиболее информативных переменных из имеющихся 15. В качестве следующего эксперимента в исходном наборе данных были оставлены эти 6 переменных, и на них проведена перекрестная проверка рассматриваемых алгоритмов, аналогичная продемонстрированной выше проверке для 15 перемен- ных. В таблице 3 представлены коэффициенты Кчув, и Кспеец, Кточ, для 6 и 15 независимых переменных. Максимальные значения коэффициентов выделены жирным шрифтом.

Из таблицы 3 видно, что при числе независимых переменных 15 коэффициенты незначительно увеличиваются.

Таблица 3. Коэффициенты моделей с 6 и 15 независимыми переменными

Table 3. Coefficients of models with 6 and 15 independent

Алгоритм Algorithm

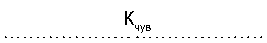
К

спеец

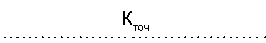
6 перемен-ных 15 перемен-ных 6 перемен-ных 15 перемен-ных 6 перемен-ных 15 перемен-ных

6 variables 15 variables 6 variables 15 variables 6 variables 15 variables

Логистическая регрессия Logistic regression

95,9                94,1

94,2              94,6              95,0

Эксперименты с рассмотренными алгоритмами, в которых из исходного набора 202 пациентов случайным образом выбирались несколько тестовых пациентов для построения их прогнозов, а остальные использовались для обучения алгоритма, подтвердили высокую точность прогнозирования исходов. Заметим, что точность прогнозирования можно существенно повысить за счет увеличения обучающей выборки.

Возникает вопрос: какой из двух подходов предпочтительнее? Ответ представляется неоднозначным. Так как оба подхода дают прогноз с практически одинаковой точностью (см. рис. 1, табл. 3), то для ответа необходимо учитывать другие аспекты построения и использования прогнозных моделей. Так, реализация построенной регрессионной модели (первый подход) в виде калькулятора позволяет сравнительно просто (Excel есть у всех) вычислить риск ускоренного развития атеросклероза. Однако построение самой модели (с отбором наиболее информативных независимых переменных) представляется более сложным по сравнению со вторым подходом, где этот выбор делается системой Orange. Кроме того, машинное обучение при построении прогнозной модели является хорошей основой (в силу простоты и компактности программирования алгоритмов обработки) при решении научно-исследовательских задач, связанных с анализом влияния данных разного объема на точность построенной прогнозной модели.

Клинический случай

Пациент К., 46 л., предприниматель, масса тела – 93 кг, рост – 176 см, перенес острый ИМ с подъемом сегмента ST нижней стенки левого желудочка в 2018 г., чрескожная транслюминальная коронарная ангиопластика (ЧТКА) со стентированием правой коронарной артерии (ПКА) в 2018 г. ЧТКА со стентированием передней нисходящей коронарной артерии (ПНА) в 2019 г., 2020 г. Тяжесть хронической сердечной недостаточности – 1-й функциональный класс по NYHA. Факторы риска: артериальная гипертензия, дислипидемия, курение (стаж – 35 лет).

На электрокардиограмме регистрировался синусовый ритм, элевация сегмента ST в III, AVF. На эхокардиограмме, проведенной на 10-е сут индексного события (ИМ в 2018 г.), выявлялся гипокинез нижней области левого желудочка, фракция выброса левого желудочка – 45%. Согласно ультразвуковому исследованию брахиоцефальных артерий, выявлены стенозы справа (45%) и слева (55%). Уровень гликемии в момент включения в исследование – 5,4 ммоль/л, креатинина – 75,6 мкмоль/л, билирубина общего – 7,6 мкмоль/л, билирубин прямой отрицателен, АЛТ – 22 усл. ед/л, АСТ – 14 усл. ед/л, калий – 3,8 ммоль/л, натрий – 138 ммоль/л, общий холестерин – 5,08 ммоль/л, триглицериды – 3,93 ммоль/л, альфа-холестерин – 1,24 ммоль/л, ЛПНП – 2,05 ммоль/л, С-реак-тивный протеин – 5 мг/л.

Пациент получал стандартную двойную антитромбо-цитарную терапию (тикагрелор и аспирин), а также бисо-пролол, статин, эзетимиб, лозап.

Согласно результатам рискометрии по калькулятору в Excel (регрессионной модели), определялся высокий риск прогрессирующего атеросклероза: вероятность составила 0,9959, а по Orangе – 0,9977.

Предсказанный прогноз подтвердился клинически у пациента в виде повторных госпитализаций по поводу нестабильной стенокардии со стентированием ПНА дважды: в 2019 и 2020 гг.

Таким образом, изложенные два подхода могут успешно дополнять друг друга, служа одной цели: построению более точных прогнозных моделей риска ускоренного развития атеросклероза.