Движение концентрационного фронта и адсорбция примеси при прокачке наножидкости через пористую среду

Моделирование процессов массопереноса веществ в пористых средах является одной из наиболее сложных задач материаловедения. Чаще всего процессы переноса в подобных материалах не вписываются в рамки классической модели «диффузии–адвекции». В общем случае пористая среда обладает сложной пространственной структурой, поэтому при математическом моделировании массопереноса требуется учет множества дополнительных механизмов. При пропитке жидкостями это может быть воздействие капиллярных сил, которые возникают в тонких поровых каналах при искривлении межфазной поверхности

в процессе их заполнения [1–3]. В случае многокомпонентных сред в роли осложняющих факторов выступают адсорбция и десорбция примеси на твердом скелете среды [4, 5]. При этом частицы взаимодействуют со стенками пор вследствие капиллярных и сорбционных явлений, что чаще всего и служит причиной замедления процессов массопереноса. Может произойти закупоривание каналов [6], которое подразумевает их частичное или полное перекрытие, что напрямую отражается на транспортировочных свойствах среды, таких как проницаемость и пористость. Дополнительное усложнение в теоретическое представление процесса фильтрации вносят неоднородности физических полей. Здесь наиболее важны пространственные распределения температуры и концентрации. Неоднородности полей обеих характеристик приводят к локальным изменениям плотности текучей фазы, насыщающей материал, что в присутствии поля тяжести «включает» дополнительный механизм массопереноса — конвекцию в пористой среде [7].

Выделение наиболее релевантных механизмов и их корректное применение при исследовании конкретного технологического процесса является основной целью данной работы. В настоящее время при производстве современных материалов с заданными свойствами в качестве основы активно используются пористые среды искусственного происхождения, которые на определенном этапе технологического цикла пропитываются многокомпонентными жидкостями с различного рода наполнителями. В зависимости от диаметра и структуры пор наполнителями могут быть порошкообразные среды с размерами частиц от микро- до нанометров. Для построения модели массопереноса частиц суспензии в материал пропитываемого изделия необходим, прежде всего, адекватный учет взаимодействия взвешенных частиц со стенками каналов. Это взаимодействие может носить чисто механический характер и представлять собой простое застревание в случаях, когда частицы или их агрегаты имеют размеры, сравнимые с поперечными размерами каналов. В этой ситуации обычно применяются статистические методы, основанные на вероятностном подходе [8], которые дают неплохие количественные результаты для среднего значения доли забитых пор и глубины проникновения частиц суспензии в пористый материал.

Когда характерный размер частиц примеси много меньше среднего диаметра поровых каналов, необходимо принимать во внимание сорбционное взаимодействие частиц суспензии со стенками. Частицы могут оседать на стенки пор, и данный процесс обычно объясняется действием ван-дер-ваальсовых сил [9, 10]. Это открывает возможность объяснить эффект замедления транспортировочных процессов: так как доля порового пространства уменьшается, снижается пористость материала и, как следствие, уменьшается его проницаемость [11]. Описание сорбционной динамики в мировой практике наиболее часто производят в рамках модели мобильно–иммобильной среды (MIM) [12], в соответствии с которой вводятся две «фазы» примеси. Одну фазу образуют свободные частицы, движущиеся в фильтрационном потоке — это мобильный компонент, вторую составляют прилипшие (или адсорбированные) частицы — немобильный компонент соответственно. Движение мобильной фазы представляется классическим уравнением диффузии–адвекции, процесс перехода частиц из одного состояния в другое — с помощью специального кинетического уравнения. Вид кинетического уравнения зависит от характера взаимодействия частиц со стенкой и средней концентрации частиц [11]. Изменение фильтрационных свойств рассматриваемой среды, сопровождающее процесс переноса частиц, может быть изображено математически по-разному. Известно не менее 15 различных подходов, позволяющих моделировать процесс закупорки, однако, большинство из них при описании конкретного эксперимента или технологического процесса базируется на эмпирических данных. Так что физически наиболее универсальна на данный момент модель Козени– Кармана [13], основанная на геометрических соображениях.

Поскольку концентрация частиц суспензии в поле силы тяжести может быть неоднородной, возникает необходимость учета их конвективного переноса, то есть требуется решение сопряженной задачи конвекции в пористой среде [14–16]. Конвекция в пористой среде — тема достаточно популярная и хорошо изученная. Наиболее простым и устоявшимся подходом для ее описания служит модель Дарси– Буссинеска [14]. Помимо «физической сорбции» частиц [9], обусловленной ван-дер-ваальсовым взаимодействием частиц с твердой границей, существуют: химическая сорбция (хемосорбция), порождаемая химической реакцией между примесью и стенкой поры [17]; гравитационное осаждение (седиментация) [18]; механическое забивание пор при поперечных размерах каналов, сопоставимых со средним размером частиц [19] и другие. Однако наиболее общим механизмом осаждения все же является физическая сорбция, поскольку она не предполагает каких-либо ограничений на структуру пористой среды, на размеры частиц примеси и вообще на примесь в целом. Единственное требование — этот механизм можно использовать для исследования закупоривания каналов при условии, что размер частиц много меньше характерного размера пор [20]. За счет адсорбционных сил примесь оседает на стенки каналов, вследствие чего снижаются пористость и проницаемость среды [21], а также скорость фильтрации. В результате на больших временах в среде может произойти фактически полное закупоривание, выражающееся в отсутствии течения. Подобные эффекты наблюдаются при заиливании колодцев и родников, засорении промышленных фильтров, ослаблении нефтеотдачи пластов [22] и другом. Как уже отмечалось ранее, в литературе состояние закупорки может описываться как механическое

«затыкание» пор крупными частицами [8, 19]. Подобный подход оправдан при решении достаточно ограниченного круга задач и не дает полной картины фильтрации.

Основная цель данной работы состояла в построении адекватной модели массопереноса частиц суспензии в рассматриваемой пористой среде. Для этого выведены уравнения в рамках некоторого подхода, выяснены условия их применимости, получено решение поставленной задачи, осуществлен его анализ для выяснения, описываются ли специфические эффекты, наблюдающиеся в ходе определенного технологического процесса. Ниже представлены результаты численного моделирования на основе предложенной модели и выполнено качественное сравнение с экспериментальными данными.

2.    Краткое описание технологического процесса

Как уже отмечалось, процесс фильтрации смеси через пористый материал, природный или созданный человеком, на практике всегда осложнен осаждением частиц примеси на твердый скелет среды. Поэтому эффект осаждения нельзя игнорировать при пропитке пористых композитных материалов суспензиями наноразмерных частиц тугоплавких соединений при создании высокотемпературных антиокислительных покрытий промышленных изделий. Реальный физический процесс был осуществлен в АО «Уральский НИИ композиционных материалов» (г. Пермь) при разности давлений на входе и выходе около одной атмосферы. За счет перепада давлений происходило прокачивание рабочей наножидкости, частицы которой характеризовались определенной дисперсией, но их размеры не превышали 100 нм. Образцы композитного материала с характерным размером пор порядка десяти микрон исследовались методом компьютерной рентгеновской томографии. Установление границ фаз и расчет объемных долей проводились в автоматическом режиме с помощью программного обеспечения CT-Analyser методом пороговой сегментации. На рисунке 1 изображен фрагмент фотографии материала с данными о распределении объемных долей различных фаз по толщине образца . Видно, что характер насыщения материала наночастицами близок к ступенчатому. Несмотря на то, что пористость практически постоянна по толщине, наибольшая доля частиц адсорбируется в приграничном слое

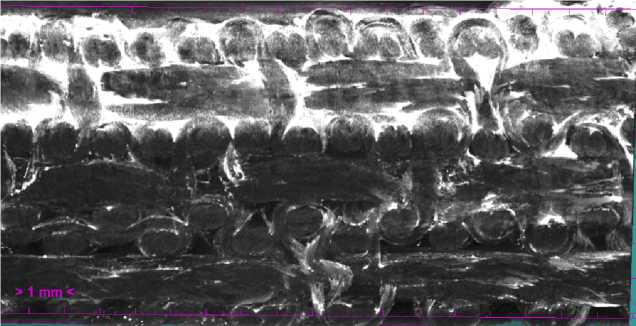
Рис. 1. Фрагмент сечения образца: белый цвет соответствует плотной фазе (наночастицам), черный – порам, серый – углеродной матрице (исходному композитному материалу)

Направление прокачивания

Опыты показали, что за относительно короткое время (порядка двадцати минут) расход жидкости резко падал фактически до нуля. В количественном выражении объем прокачиваемой за единицу времени жидкости уменьшался почти на два порядка. В то же время частицы не успевали заполнить все поры и располаглись в достаточно тонком, ярко выраженном приграничном слое (см. Рис. 1), толщина которого при продолжительности прокачки порядка 20 мин соответствовала примерно 0,1 L . После исчезновения фильтрационного потока процесс по естественным причинам прерывался, и равномерное насыщение материала наночастицами по всей толщине образца не достигалось, как это предполагалось в технологии производства материала с прогнозируемыми свойствами. Вследствие этого возникает потребность в построении модели и теоретическом анализе данного явления с целью разработки эффективных методов управления технологическим процессом.

3.    Постановка задачи и система базовых уравнений

Рассмотрим плоский вытянутый по вертикали слой толщиной L и высотой H (Рис. 2). Он изготовлен из однородного пористого материала искусственного происхождения. На его широких гранях слева и справа поддерживаются разные давления р_г >  P j, то есть имеет место их перепад A p . Слой находится

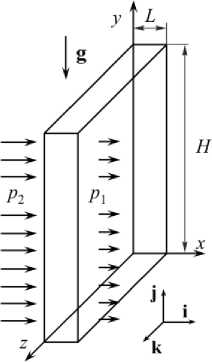
Рис. 2. Конфигурация задачи и система координат

в поле силы тяжести, что подразумевает необходимость включения в модель концентрационно–конвективного механизма переноса примеси при пропитке.

За основу возьмем систему дифференциальных уравнений в частных производных в приближении Дарси–Буссинеска, которая описывает течение жидкости в пористой среде с примесью. В дополнение примем во внимание в уравнениях возможность осаждения частиц на стенках пор. Запишем указанные уравнения с учетом особенностей так называемой линейной MIM модели и закупорки пор по механизму Козени–Кармана [23, 24]:

д

"Г. [Ф(cm + ci )] = -vVcm + DА(фcm ) , д t

д

dt ci =^( cm , ci ) , где t — время, V — оператор набла, А — оператор Лапласа, c , c — объемные концентрации тяжелой примеси, соответственно, в мобильной и иммобильной фазах, v — скорость фильтрации; ф — пористость среды, D — коэффициент диффузии в отсутствие твердого скелета. Правая часть второго уравнения ^(cm, c) — это кинетическая функция, описывающая динамику перехода примеси из одной фазы в другую, а именно из мобильного состояния в иммобильное и обратно.

Переформулируем уравнения (1) в терминах поровой скорости, которая представляет собой «действительную скорость движения жидкости по поровым трубкам» [15]. Согласно закону Дарси (в записи через поровую скорость) и при условии несжимаемости жидкости имеем систему уравнений вида:

д t ( cm + ci) = -( uV) cm + DА cm , u + gCmPpj = -VP , divu = 0 ,

к ( ф )

д tci=a( cm (q 0 - ci ) - KdCi) ,

к(ф) = коф3/(1-ф)2 ,     ф = ф0 -ci, где к — проницаемость среды (функция пористости), u — поровая скорость жидкости, P — добавка к гидростатическому давлению. Помимо полей, подлежащих определению, в уравнения входят: в — коэффициент концентрационного увеличения плотности, а — параметр межфазного обмена, р — плотность жидкости-носителя, к0 — константа Козени-Кармана, ф0 — пористость незагрязненной среды, K — коэффициент распределения примеси [5], g — величина ускорения силы тяжести, j — единичный вектор, ориентированный вертикально вверх (Рис. 2), q — концентрация насыщения пористой среды.

Из полного эволюционного уравнения для пористости вытекает уравнение несжимаемости для поровой скорости. Но в его записи, приведенной в (3), отсутствуют слагаемые, которые пропорциональны относительному изменению пористости во времени или в пространстве. Однако, как показано в [25], для рассматриваемого процесса такая запись правомерна: если ввести вариацию пористости 5ф , то эти слагаемые будут содержать в качестве множителя отношение 5ф/ф , которое мало. Даже в случае, когда по мере закупорки ф ^ 0, вариация 5ф стремится к нулю еще быстрее. Иными словами, поле поровой скорости с хорошей точностью можно считать безвихревым.

Однако полностью игнорировать изменение пористости при насыщении пористой среды частицами нельзя. Так как пористость однозначно связана с проницаемостью, эффект ее уменьшения в ходе закупорки необходимо оставить в формуле Козени–Кармана. В используемой модели (2)–(5) вариация пористости всегда, в каждый момент времени, сказывается на вариации проницаемости. Такое приближение в некотором смысле аналогично приближению Буссинеска для вариации плотности, когда в законе сохранения массы изменениями плотности пренебрегают, а в уравнении Навье–Стокса в слагаемом с подъемной силой изменение плотности в зависимости от температуры учитывается. Подробный анализ системы уравнений (2)–(5) проделан в работе [25].

В рамках MIM подхода предполагается, что примесь разделена на две фазы: мобильную (дрейфующую в фильтрационном потоке) и немобильную (осевшую на твердый скелет среды). Очевидно, что пространственный перенос примеси обусловлен исключительно динамикой мобильной фазы. Адсорбировавшаяся внутри пор примесь уменьшает объем порового пространства. Согласно предложенной модели пористость во втором уравнении (5) линейно зависит от объемной концентрации примеси, находящейся в немобильной фазе. При этом гидродинамическое сопротивление течению через поры увеличивается. Таким образом, осаждение примеси сказывается на проницаемости среды. Модель неплохо описывает геологические процессы фильтрации, для которых характерны крайне малые скорости. Время, которое отводится на осуществление процесса насыщения, как правило, ограничено, и, по возможности, оно еще и минимизируется. Поэтому в рабочем режиме обсуждаемая технология предусматривает достаточно большие перепады давления, что на начальном этапе порождает в «незагрязненной» среде значительные скорости фильтрационного потока. В этом случае простейшая линейная связь (4) между приращением концентрации иммобильного компонента и самими концентрациями мобильной, а также иммобильной фаз не вполне корректно отражает динамику перераспределения примеси. А именно, в ходе интенсивной фильтрации начинают играть роль нелинейные эффекты, и по этой причине для адекватного описания процесса прокачки требуется корректировка классического MIM подхода. Следуя [26], введем дополнительную нелинейность ~ uc в виде обратной связи, когда закупорка в еще большей степени уменьшает поровую скорость и тем самым усиливает адсорбцию примеси и ускоряет процесс наполнения пор. Перегруппировав в (4) слагаемые и переобозначив материальные константы, получим уравнение вида:

d tci=a( cm ( q 0 -C,-)-Y( ux - uc ) ci) . (6)

Иными словами, когда скорость u падает до критического значения u , адсорбция максимально возрастает, и насыщение пористой среды усиливается. Коэффициент y описывает обратное влияние потока на адсорбционные процессы.

З а м е ч а н и е 1. При расчетах последнее слагаемое в уравнении (6) учитывалось локально в каждом узле сетки только при условии u_x >  п_с. так как десорбционное слагаемое может приводить только к уменьшению концентрации иммобильного компонента. Математически добавленное слагаемое означает, что коэффициент десорбции, который ранее был константой, теперь зависит от скорости течения в порах, что представляет собой дополнительную нелинейность в системе уравнений.

Обезразмерим систему модифицированных уравнений (2), (3), (5), (6) с помощью следующих естественных для данной задачи переменных: для единиц измерения [ A x , A y ] = L . для времени [ t ] = LD . для поровой скорости   [ u ] = D/L. для давления [ P ] = Р ₂ - Р_г  для концентрации примеси [ c ] = С_о

(концентрация насыщения пористой среды q обезразмеривается так же, как концентрация примеси). Здесь x и y — соответственно, горизонтальная и вертикальная координаты (см. Рис. 2), которые отнесем к толщине пластины L . За единицу концентрации берется начальная концентрация примеси C на левой границе; P и P — давления на входе и выходе соответственно. Существенным является наличие в (6) нелинейного слагаемого, содержащего скорость u , которое позволяет учесть обратное влияние пористой среды на скорость фильтрации.

В результате обезразмеривания система уравнений приобретает модифицированный вид:

St ( cm + ci ) = —(uV) cm +A cm .

-ur + RP Cm j = - PeVP .    div v = 0 .

к ( ф )

d tci = acm ( q 0 — ci)-b (ux — u ) ci .      к(ф) = ф3/(1 -ф)2 .      ф=ф0 - C0 Ci-

Для замыкания системы уравнений (7)–(9) дополним ее граничными условиями тоже в безразмерной форме:

"xlx=0 =-Pek(ф)|x=05,Px=0.     «,[,=0„ = 0 .(10)

C.lx =0 = C0.      d xCmlx., = 0 .      d.C.|y =„,, = 0 .(1

Plx=0 = I-    Plx=,= 0.    dP =., =— RPP=0,. .( где h — безразмерная высота образца. В систему уравнений (7)–(9) и граничных условий (10)–(12) также входят следующие критерии подобия: параметры адсорбции и десорбции — a и b , числа Пекле и Рэлея– дарси — Pe и Rp :

a = _a CL ,     b = _a KL ,    Pe = ( P ²   P ^{1 ) k} ° ,    Rp = g P^ o P LC o. .

D          D           D пФ о             D ПФ о

Константы a и b характеризуют интенсивность адсорбционных и десорбционных процессов в пористой среде, число Пекле описывает интенсивность прокачки в системе, а так называемое число Рэлея–Дарси отвечает за действие силы тяжести на элемент прокачиваемой жидкости в зависимости от его плотности.

Первое краевое условие в (10) и последнее в (12), которые следуют из уравнения Дарси–Буссинеска, являются динамическими, так как скорость, давление и проницаемость на левой и правой границах расчетной области зависят не только от высоты, но и от времени. Второе условие в (11) — ограничение на концентрацию мобильной примеси, требует особого обсуждения и означает, что вся примесь, доходящая до правой границы, выносится без задержки вместе с потоком.

4.    Методика решения

Система дифференциальных уравнений в частных производных (7)–(9) совместно с краевыми условиями (10)–(12) решалась методом конечных разностей на постоянной по пространству сетке. При этом два уравнения для компонент скорости в законе Дарси (8) были преобразованы в уравнение Пуассона для давления. Уравнение получило довольно сложную правую часть, поскольку проницаемость является функцией пористости, которая в свою очередь зависит от координат и времени. Ввиду громоздкости и малой наглядности это уравнение в тексте статьи не приводится.

Алгоритм численного решения был разработан в соответствии с явной схемой решения эволюционных квазилинейных уравнений в частных производных [27]. При аппроксимации производных по времени и производных по координатам использовались, соответственно, односторонние и центральные разности. Шаг по времени выбирался из соображений устойчивости численной процедуры и вычислялся по формуле A t = min ( A h ,²,A h ² )Д 4 ст ) [27]. Здесь в соответствии с теорией устойчивости явной схемы A h_x , A h — шаги вдоль осей x и у , ст — эмпирический параметр ( ст >  1 ) . При решении уравнения Пуассона для давления использовался метод последовательных приближений. В ходе расчетов по времени применялась процедура установления. Авторский компьютерный код был реализован на языке программирования FORTRAN-90. При проведении численного моделирования осуществлялась периодическая запись искомых полей концентрации мобильной и иммобильной примеси, компонент поровой скорости, давления, пористости и проницаемости среды на диск, что позволяло анализировать движение концентрационного фронта, распределение скорости и давления в массиве, а также структуру пористого скелета в каждый момент времени.

Начальными условиями в расчетной области служили невозмущенные поля давления ( P = 0), скоростей ( и_х =0, и =0), пористости (ф₀ = 0,5 ), проницаемости ( к = 0,5 ), а также концентраций мобильной и иммобильной фаз ( С_т = С = 0). Возмущения в поля концентрации мобильной примеси и давления в начальный момент времени не вносились, однако на левой границе задавалось давление P , избыточное по отношению к давлению на правой границе. Последнее принималось за начало отсчета: P = 0. Также устанавливалось значение концентрации на входе ( С _о), чтобы начальный градиент соответствовал процессу просачивания слева направо. В расчетах по координатам x и y использовалась рабочая сетка с числом узлов на единицу длины 35 + 155. В ходе тестовых расчетов рассматривалось разное соотношение размеров образца: H/L = 5 + 10. Ниже представлены результаты расчета насыщения слоя при H/L = 5 .

5.    Обсуждение результатов

На рисунке 3 приведены двумерные векторные поля скорости фильтрационного движения для разных моментов времени. Эти результаты численного моделирования, включая все представленные далее данные, использованные в расчете, соответствуют фиксированным значениям безразмерных параметров: Rp = 30, Pe = 800 , a = 600 , b = 20, Co = 1,0, ф0 = 0,5 , q0 = 0,45 . Первые два отвечают параметрам водно-спиртовых растворов [28]. Так как частицы достаточно тяжелые, примем р ~3, их концентрация не является малой и составляет 0,2 массовой доли, v = 2 х10 6 м2/с, к0 = 10 14 м2, L = 10 2 м, D = 10 10 м2/с, р = 103 кг/м3. Таким образом, число Рэлея-Дарси равно Rp ~ 30 . При разности давлений P - р = 2 -103 Па число Пекле составляет: Pe ~ 1000 . Безразмерные параметры адсорбции и десорбции для частиц размером менее 100 нм неизвестны, поэтому в ходе численного моделирования они подбирались так, чтобы обеспечить согласие результатов расчета и данных технологического процесса. Значение критической скорости в расчетах принималось равным ис = 350 . При переходе к размерным величинам для указанных выше коэффициента диффузии и толщины слоя это дает весьма малое значение — порядка 5-10-3мм/с. Но оно неплохо согласуется с исходными предположениями о механизме отрыва, который происходит при превышении силами вязких напряжений (действуют на частицу со стороны потока) сил ван-дер-ваальсового взаимодействия со стенкой. Величина критических напряжений оценена в работе [29]. Критические напряжения для различных сочетаний материалов частицы и стенки имеют порядок ~10-2Па, что для поры размером ~10-5м, соответствует диапазону скоростей 10-2^10-3мм/с.

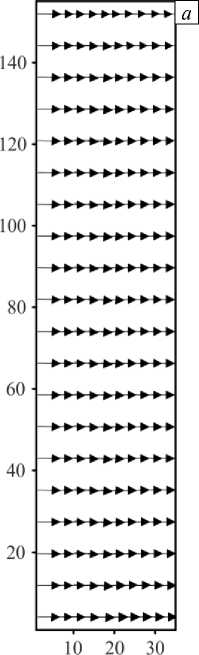
Рис. 3. Поля скорости в разные моменты времени t : 0,002 ( а ); 0,005 ( б ); 0,01 ( в )

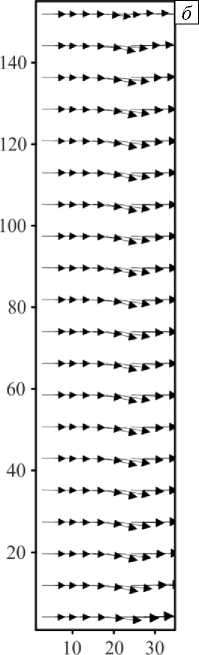
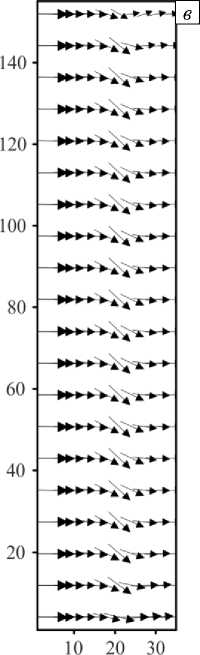
Показанная картина течения является весьма характерной и позволяет принципиально оценить действие силы тяжести на поток без существенного перебора параметров. Видно, что уже при умеренных значениях числа Рэлея–Дарси сила тяжести начинает постепенно искривлять поле скорости. Конечно, с ростом скорости прокачки это влияние уменьшается, но на больших временах, когда скорость фильтрации падает за счет обрастания стенок пор частицами, этот эффект все равно наблюдается. Линии тока «проседают» в середине образца, то есть симметрия течения «верх–низ» нарушается. Тем не менее, рисунок 3 показывает, что линии тока не сильно меняют кривизну при рассматриваемой прокачке в том смысле, что ни о какой развитой конвекции в виде возвратных течений при данных числах Пекле речи идти не может. Концентрационно–конвективный механизм хоть и вносит некоторый вклад в характер линий тока, но, что очевидно, не играет доминирующей роли в ходе прокачки при таких больших числах Пекле. Поле концентрации иммобильного компонента (Рис. 4) вообще визуально никак не меняется вследствие искривления линий тока. Расчетное время t = 0,009 безразмерных единиц, соответствующее полю справа на рисунке 3 в , при толщине слоя 1 см и коэффициенте диффузии D = 10 ^{- 10} м²/с составляет примерно два с половиной часа. По мере продвижения мобильного компонента вместе с фильтрацонным потоком примесь за счет адсорбции оседает на порах скелета материала.

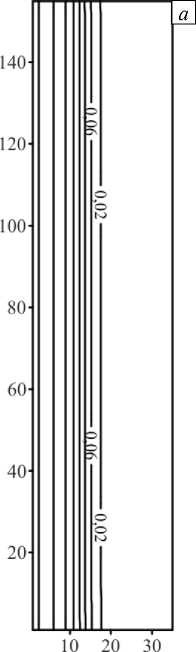
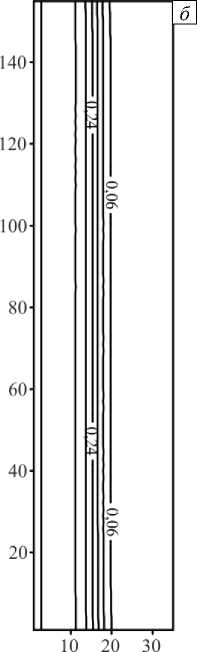
Рис. 4. Поля концентрации иммобильного компонента в разные моменты времени t : 0,002 ( а ); 0,005 ( б ); 0,009 ( в )

Стенки пор достаточно быстро обрастают частицами, и скорость фильтрационного потока резко уменьшается практически на два порядка (Рис. 5). Кардинальное уменьшение скорости происходит за безразмерное время порядка t = 0,003 (50 мин), но, как показывают расчеты, скорость не падает до нуля. Медленно, но процесс фильтрации продолжается и на больших временах, вплоть до t = 0,1 (28 часов), что хорошо согласуется с опытом.

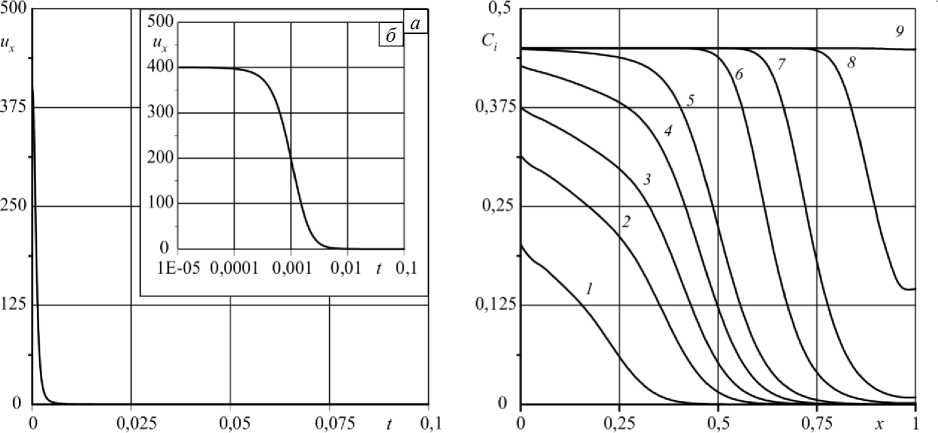
Рис. 6. Распределение концентрации иммобильной фазы вдоль оси x на высоте у = 2,5 при значениях безразмерных параметров как на рисунках 3, 4 в моменты времени t : 0,001 (кривая 1 ); 0,002 ( 2 ); 0,003 ( 3 ); 0,005 ( 4 ); 0,01 ( 5 ); 0,05 ( 6); 0,1 ( 7 ); 0,2 ( 8 ); 0,3 ( 9 )

Рис. 5. Временная зависимость x -компоненты поровой скорости в точке с координатами x = 0,5 у = 2,5 (середина образца) ( а ) и ее фрагмент в увеличенном масштабе ( б ) на начальном этапе процесса фильтрации при значениях управляющих параметров как на рисунке 4

С точки зрения пропитки материалов наибольший практический интерес вызывает распределение концентрации осевших наночастиц в зависимости от времени, то есть эволюция поля иммобильной примеси. Характер концентрации в разные моменты времени хорошо прослеживается по кривым, приведенным на рисунке 6. Наблюдается ярко выраженный концентрационный фронт, который очень похож на то, что экспериментально установлено и представлено на рисунке 1. То есть в начальный момент времени распределение примеси представляет собой тонкий приграничный слой, а далее это ступенчатое распределение начинает двигаться.

Первоначально проникновение наночастиц в поры имеет в некотором смысле «клинообразный» характер, а именно: сначала примесь довольно быстро проникает вглубь материала на небольшое расстояние, так что концентрация мобильной примеси плавно убывает практически до нуля на расстоянии, равном толщине приграничного слоя. В этом приграничном слое сразу начинается процесс адсорбции, и, как следствие, включается механизм обратного влияния иммобильной примеси на адсорбционный процесс и, соответственно, на скорость фильтрации. С ростом концентрации иммобильной примеси в приграничном слое скорость фильтрации резко падает, в результате этого возникает укручение концентрационной волны, и появляется резко выраженная граница у фронта иммобильной примеси. Значение концентрации иммобильной примеси относительно быстро достигает пороговой величины, и скорость уменьшается более чем на два порядка. Тем не менее, как уже было отмечено выше, процесс фильтрации не прекращается полностью, а концентрационный фронт медленно, но неуклонно продолжает продвигаться вглубь пористого образца. При этом опрокидывания концентрационного фронта не наблюдается.

Не менее важно для анализа поле мобильного компонента. В рамках предложенной модели расчеты приводят к весьма неожиданному эффекту. Оказывается, что профиль концентрации мобильной фазы вблизи входа ведет себя с течением времени немонотонно (Рис. 7). В некоторой фиксированной точке рядом с левой границей на расстоянии примерно 0,2 от общей толщины слоя концентрация мобильной примеси сначала достаточно быстро возрастает, а затем поры начинают опустошаться. На следующем — финальном — этапе концентрация мобильной фазы в пористой среде снова демонстрирует тенденцию к увеличению, но теперь медленному вплоть до состояния насыщения. Этот эффект объясняется конкуренцией конвективного переноса и адсорбции: на начальном этапе концентрация мобильной примеси быстро растет по причине большой скорости фильтрации в незагрязненной пористой среде, когда, вследствие конвективного переноса, прибыль в рассматриваемом элементарном объеме превосходит переход из мобильной фазы в иммобильную. После того как начинается адсорбция (особенно интенсивна она вблизи левой границы, так как концентрация мобильного компонента там больше), скорость просачивания нелинейно падает, и конвективный перенос уменьшается до такой степени, что адсорбционные потери начинают превосходить поступление примеси с левой границы. На этом этапе концентрация мобильной фазы начинает убывать.

Уменьшение мобильной фазы в рассматриваемом элементарном объеме имеет место до определенных пределов, а именно до тех пор, пока концентрация иммобильной фазы не выйдет на насыщение. После этого концентрация осевшего на стенки компонента практически перестает расти, то есть на этом этапе нет

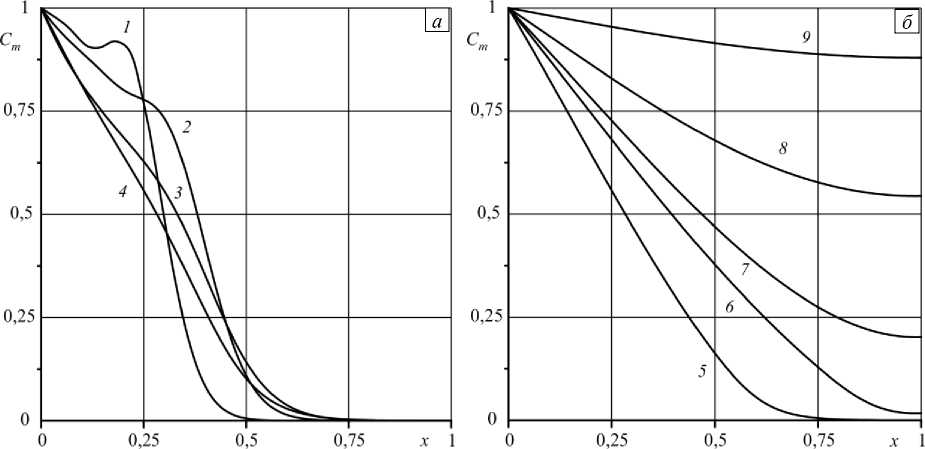
Рис. 7. Распределение концентрации мобильной фазы вдоль оси x на высоте у = 2,5 при значениях безразмерных параметров как на рисунке 5 в моменты времени t : 0,001 (кривая 1 ); 0,002 ( 2 ); 0,005 ( 3 ); 0,01 ( 4 ) ( а ); 0,05 ( 5 ); 0,2 ( 6) ; 0,3 ( 7) ; 0,5 ( 8 ); 1,0 ( 9 ) ( б )

новых поступлений из мобильной фазы. В результате, за счет продолжающегося конвективного притока, концентрация мобильной фазы снова начинает увеличиваться и далее постепенно выходит на насыщение. Из сравнения содержимого рисунков 6 и 7 вытекает, что распределение концентрации иммобильного компонента синхронно, что вполне закономерно, следует за полем концентрации мобильной примеси, то есть мобильная фаза тоже не сразу достигает противоположной границы.

В то время как концентрации мобильного компонента и осевшей в порах примеси уменьшается с ростом координаты x , распределения пористости и проницаемости, наоборот, наименьшее значение имеют на входе в образец (Рис. 8). Поля пористости и проницаемости тоже синхронно изменяются с течением времени. Так и должно быть, поскольку локально пористость и проницаемость в каждый момент времени однозначно связаны формулой Козени-Кармана.

Численное моделирование для разных чисел Пекле показывает, что с его ростом характерное «проседание» линий тока по-прежнему возникает после падения скорости прокачки в результате закупорки каналов, но этот излом линий тока сдвигается вглубь образца. Также вполне закономерно и то, что по мере увеличения числа Пекле концентрационный фронт движется более быстро. Как оказалось, рост скорости движения даже на начальном этапе обуславливает в дальнейшем более быстрое распространение как мобильной, так и иммобильной примеси.

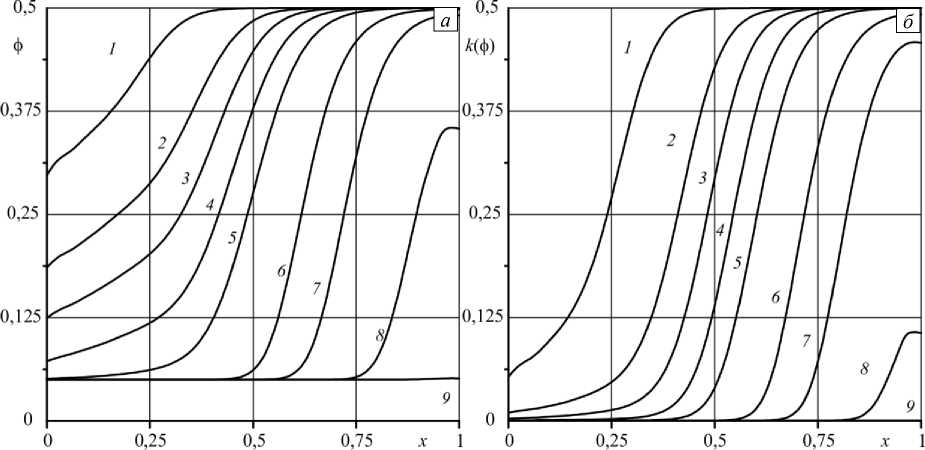
Рис. 8. Распределение пористости ( а ) и проницаемости ( б ) вдоль оси x на высоте у = 2,5 при тех же значениях безразмерных параметров как на рисунке 5 в моменты времени t : 0,001 (кривая 1 ); 0,002 ( 2 ); 0,003 ( 3 ); 0,005 ( 4 ); 0,01 ( 5 ); 0,05 ( 6 ); 0,1 ( 7 ); 0,3 ( 8 ); 0,3 ( 9 ) ( б )

В ходе численного моделирования также проведено исследование влияния неоднородности концентрации наночастиц в рабочей жидкости на входе в слой, что актуально для реальных условий эксперимента. Изначально при расчете предполагалось, что на левой границе образца концентрация мобильного компонента однородна. Совершенно очевидно, что в опыте это требование трудновыполнимо. Разнообразные неконтролируемые неоднородности полей на входе в образец могут стать причиной развития различного рода неустойчивостей и неожиданных последствий [30]. В частности, при течении многокомпонентных несмешивающихся жидкостей в пористых средах развитие малых возмущений может приводить к образованию пальцеобразных структур, причиной возникновения которых является так называемая морфологическая неустойчивость границ раздела.

Таким образом, представим результаты дополнительного численного исследования, которые моделируют эволюцию малых возмущений, искусственно вносимых в поток на входе. Пусть теперь на входе в слой поле концентрации мобильного компонента неоднородно и описывается периодической функцией вида

c

m

I x = 0 = C о 1 ¹ + A o sin

2 п ny h

Здесь n — целое число, отвечающее за периодичность концентрации на входе, A — амплитуда возмущения. Далее представим результаты расчетов для A = 0,05 (Рис. 9, 10).

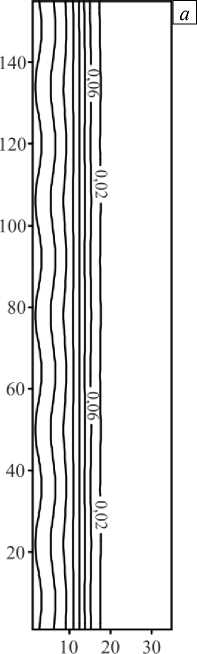
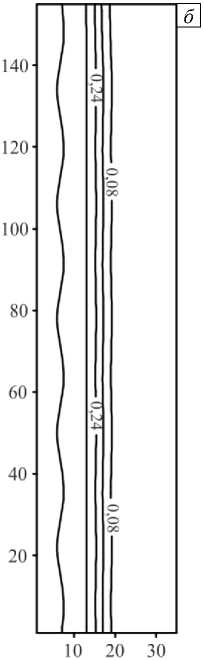
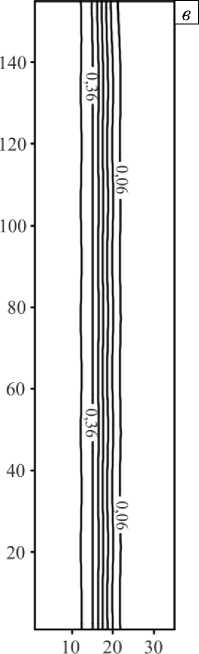
Рис. 9. Эволюция поля концентрации иммобильной фазы при неоднородном распределении примеси на входе в разные моменты времени t : 0,002 ( а ); 0,005 ( б ); 0,009 ( в )

140-
120 •—*^
100- —►►>
80	►г*^ж*~*~*^
60-—^
40 •
20- н->
10	20 30

в

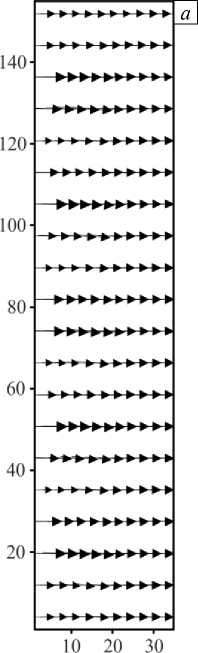
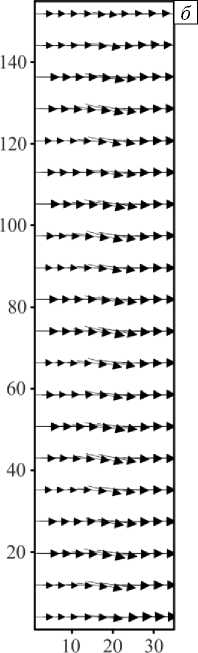
Рис. 10. Поля скорости при неоднородном распределении примеси на входе в разные моменты времени t : 0,002 ( а );

0,005 ( б ); 0,009 ( в )

На начальном этапе по времени неоднородности поля концентрации на входе сильно искажают распределение иммобильного компонента, но на больших временах, когда система выходит на насыщение, все неоднородности примеси сглаживаются и система «забывает» о внесенных ранее в поток возмущениях. На левой границе в момент времени t = 0,001 (Рис. 9 a ) имеем сильно неоднородное поле концентрации. Но в последующий момент времени t = 0,03 , когда появляется «полочка» насыщения (см. Рис. 9 б, в ), исходная периодичность в поле концентрации на левой границе пропадает. Распределение иммобильного компонента выравнивается, то есть вносимые в поток возмущения не нарастают, а, наоборот, затухают с течением времени.

З а м е ч а н и е 2. Неожиданно, но поле силы тяжести тоже не усиливает начальные возмущения, вносимые в распределение мобильной фазы, которая представляет собой более тяжелый компонент, нежели несущая жидкость (Рис. 10).

Таким образом, при реализации технологического процесса фактор недостаточно перемешанного в начальный момент времени коллоидного раствора не может сыграть решающей роли при возникновении неоднородностей в концентрационном поле иммобильного компонента. Расчеты показывают, что рассматриваемая диссипативная система быстро «забывает» о неоднородных начальных условиях и довольно скоро выходит на установившийся режим медленного перемещения концентрационного фронта к правой границе образца.

6.    Рамки применимости модели

Оценим границы применимости теории, предлагаемой для описания процесса пропитки композитного материала суспензиями, содержащими наночастицы тугоплавкого материала, на примере диборида циркония. Эти частицы взаимодействуют со стенкой поры по механизму Ван-дер-Ваальса [10]. Тогда потенциальная энергия взаимодействия определяется из выражения:

A а а , f h — — +--+ ln I -----

6 h h + 2 а    I h + 2 а

Здесь A — так называемая константа Гамакера, a — радиус частицы, h — расстояние от поверхности частицы до стенки. Частица может подойти к стенке на расстояние не ближе, чем размеры молекул жидкости, а именно h ~0,5 - 10 9 м. В рассматриваемом приближении радиус частиц много больше h , поэтому очевидно упрощение уравнение (14):

Aa

.

E v "^

6 h

Для определения константы Гамакера при взаимодействии диборида циркония и углеродного волокна воспользуемся выражением [31]:

27 E 1 E ₂   (_{£ 1} - 1 )^ - 1 )

32 E + E2 (S1+ 2)(e2+ 2) ,

где £j, e2 — резонансные значения диэлектрической проницаемости диборида циркония и углеродного волокна соответственно, а E , E — энергии кванта электромагнитного излучения, при которых достигаются соответствующие значения диэлектрических проницаемостей. Оценим константу Гамакера (16) на основании работы [31]. Значения Ex = 2,5 -10-19 Дж и с ® 3,5 соответствуют дибориду циркония, а значения E2 = 5 -10-19 Дж, £2 « 6 справедливы для углеродного волокна на основании работы [32]. Для указанных значений энергий и диэлектрических проницаемостей константа Гамакера составляет: A ® 4 -10-20 Дж. Отрыв частицы от стенки происходит благодаря тепловым флуктуациям и срыву частицы потоком.

Далее найдем величину энергии тепловых флуктуаций [33]. Из законов статистической термодинамики следует, что

E = -кг « 6 - 10 ^{- 21} Дж.

Это на порядок меньше константы Гамакера, а поскольку a/h >> 1, то по порядку величины имеем следующее соотношение: Е >> A >> Et. Оно означает нецелесообразность учета тепловых флуктуаций в силу их несущественности. Кинетическая энергия, которой обладает частица во внешнем потоке, может быть записана как m 0 V2  4 пр а3 Г АР к Y

,

E, k   2   32 ( L пФ)

где m₀ — масса частицы, V — ее скорость, р — плотность диборида циркония, А Р — перепад давления при прокачке, L — толщина образца, к — проницаемость образца, п — вязкость несущей жидкости, ф — пористость среды. Таким образом, необходимо сопоставлять E_v и Е_к (см. (15) и (17) соответственно). Из условия баланса энергий E_v ® Е^ получим формулу для вычисления критического радиуса частицы:

_ A L пф у 4пр h АР к

.

Подставим значения параметров, характерные для рассматриваемого процесса: перепад давлений в ходе пропитки А Р — 10 5 Па, L — 10 ^{- 2} м, п — 10 - 3 Па - с, к — 10 ^{- 14} м² (оценка по формуле Козени), ф — 0,3 , р — 6 г/см³, h — 10 9 м, A — 4 - 10 ^{- 20} Дж. В результате для радиуса частицы имеем: а ® 2 - 10 ^{- 5} м или 20 мкм.

На основании этих рассуждений можно сделать вывод, что предложенная модель фильтрации с учетом адсорбции примеси на стенках пор композитного материала применима, если частицы имеют радиус меньше 20 мкм. Применительно к рассматриваемым пористым средам с диаметрами каналов порядка 10÷50 мкм при использовании частиц размером менее 100 нм предлагаемая модель тоже оказывается вполне приемлемой. Еще одним необходимым условием применимости данной теории для адекватного описания процессов пропитки пористых материалов является требование, согласно которому в ходе пропитки наночастицы не должны образовывать кластеры. Для того чтобы избежать этого, в реальных опытах обычно используют специальные вещества — стабилизаторы, оптимальный подбор которых применительно к конкретной наножидкости выходит за рамки рассматриваемой физико-математической модели.

7.    Заключение

Предложена модель массопереноса наночастиц суспензии в процессе насыщения модельных пористых сред искусственного происхождения. Показано, что при соответствии свойств суспензий заявленным требованиям по размерам частиц, основным механизмом закупорки пор является физическая сорбция, то есть взаимодействие частиц со стенками поровых каналов обеспечивается силами Ван-дер-Ваальса.

Разработан метод решения задачи, составлен программный код, моделирующий проникновение суспензии в прямоугольный образец. Результаты расчетов показали, что основной фактор, влияющий на форму течения и закупорку среды — это нелинейное взаимодействие потока с пористым материалом, а также перепад давления между границами преформы.

Показано, что обратное влияние скорости фильтрации на сорбционные свойства приводит к образованию круто изогнутого фронта имммобильной составляющей, скорость движения которого растет с увеличением перепада давления.

Выявлено, что искажения, возникающие при учете гравитационного перераспределения примеси, а также искусственно вносимые в поток возмущения сглаживаются, и характеристики фильтрационного процесса с течением времени становятся более равномерными по толщине образца.

В результате анализа влияния конвективного переноса примеси установлено, что для перепада давления в пределах рабочего диапазона значений конвекция не вносит существенного вклада в массоперенос.

Работа выполнена при финансовой поддержке Министерства образования и науки Пермского края (соглашение № С-26/788).