Движение спутника-гиростата, содержащего полость с жидкостью большой вязкости

Динамика движения твердых тел и космических аппаратов (КА) с полостями с жидкостью исследовалась в работах Жуковского Н.Е. [1], Черноусько Ф.Л. [2], Моисеева Н.Н. [3], Рабиновича Б.И. [4, 5], Нариманова Г.С., Докучаева Л.В. [6] и других авторов. К настоящему времени глубоко изучено движение твердых тел с полостью, содержащей жидкость различной вязкости, заполняющей полость полностью либо частично, в линейной и нелинейной постановках, и получены важные результаты по оценке устойчивости различных режимов возмущенного движения. Исследованию движения систем тел с жидкостными компонентами не уделено должного внимания. Поэтому ставится задача исследования движения таких систем. Решение данной задачи важно с прикладной точки зрения при изучении движения спутников-гиростатов и КА с гироскопической стабилизацией.

Математическая модель движения

Рассмотрим движение трехроторного гиростата с полостью в несущем теле, содержащей жидкость большой вязкости, который в дальнейшем будем называть гиростатом с полостью с жидкостью. Введем следующие системы координат [7, 8] (рис. 1): OXYZ – ке-нигова система координат; Oxiyizi и Oxyz – системы координат, связанные с роторами 1–3 и несущим телом 4, соответственно. Оси Ox, Oy, Oz являются осями вращения роторов (тела 1–3). Положение несущего тела относительно системы OXYZ будем характеризо- вать эйлеровыми углами: ψ, θ, ϕ.

Угловая скорость несущего тела ω = ( p, q, r ) представлена в проекциях на оси Oxyz , а векторы угловых скоростей роторов ω _i = ( p_i, q_i, r_i ) – на оси собствен ны х связанных систем координат Ox_iy_iz_i ( i = 1,3). Относительное движение роторов характеризуется углами и скоростями относительного закручивания 5 i = O i (рис. 1).

Компоненты векторов угловых скоростей роторов ω _i , выраженные через компоненты p, q, r угловой скорости тела-носителя, имеют вид:

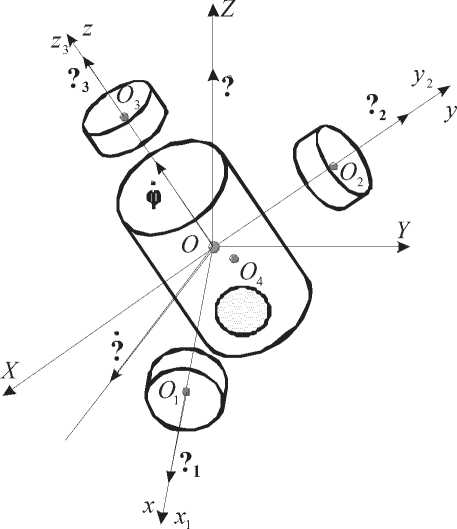
Рис. 1. Схема гиростата с полостью и используемые системы координат

' Р 1 = p + O "1 ,

* q 1 = q cos 5 1 + r sin 5 1 r 1 = r cos 5 1 - q sin 5 1 ,

где E – единичная матрица, D – постоянная

p 2 = p cos 5 2 - r sin 5 2 ,

* q2 = q + a2, r2 = r cos 52 + p sin 52,

p 3 = p cos 5 3 + q sin 5 3 , * q 3 = q cos 5 3 - p sin 5 3 , r ₃ = r + a 3 .

Для получения уравнений движения системы тел воспользуемся теоремой об изменении кинетического момента, выбирая в качестве полюса О центр масс системы:

dK O = M dt O .

Пусть рассматриваемая система включает в себя три одинаковых динамически симметричных ротора и динамически несимметричное тело-носитель с полостью с жидкостью. Главные моменты инерции роторов (тела 1–3), вычисленные в свои х связанных системах координат Oxyz. ( i = 1,3), обозначим A_i , B_i , C_i , а моменты инерции тела-носителя в системе координат Oxyz – A₄ , B₄ , C₄ . Введенные моменты инерции не являются центральными, так как начала связанных с телами систем координат совпадают с центром масс системы четырех тел. Осевые моменты инерции роторов равны друг другу: A₁ = B₂ = C₃ = I .

Пусть жидкость внутри полости имеет большую кинематическую вязкость ν ( ν >> 1), что соответствует малым числам Рейнольдса Re ~ v ^{- 1} <<  1. Введем малый параметр, характеризующий величину числа Рейнольдса p = pv ^{- 1} <<  1, где с - плотность жидкости. Полость с жидкостью характеризуется тензором D = D } [2], который зависит лишь от ее формы и определяет диссипацию энергии за счет вязкости жидкости. Компоненты D_ij вычисляются в системе координат, связанной с несущим телом. Пусть полость является сферической, тогда указанный тензор записывается следующим образом: D = О E ,

величина.

Кинетический момент системы относительно центра масс равен векторной сумме кинетических м о ментов несущего тела K ₄, роторов K i ( i = 1,3) и гиростатического момента жидкости L относительно точки О :

K о = £ K i + L .

i = 1

Вычисляя производную кинетического момента системы как суммы кинетических

моментов тел и жидкости, используя при этом

локальные производные в связанных систе-

мах Ox_iy_iz_i, и Oxyz , уравнение (3) можно за-

писать в системе Oxyz [7, 8]:

Z 8 i i=1

d K _i dt

+ to i x K i

—

~

dL

---+ to x dt

L

где знак “~” обозначает локальную производную в соответствующей подвижной системе координат, K _i = ( A_ip_i, B_iq_i, C_ir_i ), K ₄ = ( A₄p, B₄q, C₄r ) – к и нетические моменты твердых тел, 8 i ( i = 1,3) - матрицы перехода от систем координат Ox_iy_iz_i к системе Oxyz (поворот на угол д_i вокруг соответствующей оси), 8 4 = E , to 4 = to .

С учетом (1) система (3) в скалярном виде запишется следующим образом:

Ap + ( С - B ) qr + Io\ + 1 ( qa 3 - ra ₂ ) = m x ,

^Bq + ⁽ A ^{- С} ) pr + I(j 2 + I ⁽ r^a 1 ^- p^a з ) = m y , (4) Cr^- + ( B - A ) pq + Id 3 + 1 ( pa ₂ - qr 1 ) = m_z ,

где A = Z A , B = Z Bi , C = Z C i . Правые i = 1                    i = 1                    i = 1

части уравнений (4) представляют собой проекции момента сил, действующих на несущее тело со стороны полости с жидкостью:

m = -

~

dL

---+ to x dt

L

Гиростатический момент жидкости, следуя работе [2], будем определять по формуле:

L = - ^p D ■ co = - pD E • co

ν где (b = (p, (q, r) - вектор углового ускорения несущего тела. В этом случае выражение (5) можно переписать в виде:

m = - pP g , где m = ( m x , m y , m_z ) T , а

p + qr - rq g =

q + rp - pr

r + pq - qp

Уравнения относительного движения роторов, соответствующие углам относительного закручивания дi также могут быть получены из теоремы об изменении кинетического момента каждого из роторов:

I (p + oi ) = Mx , I (q + o 2 ) = My , I (r + o 3 ) = Mz ,

где M_w ( w = x, y, z ) – момент, действующий со стороны несущего тела на ротор, установленный вдоль соответствующей оси. Будем рассматривать движение при отсутствии указанных моментов взаимодействия тел. Тогда система (7) приводится к следующему виду:

o = -p, o2 = -q, o3 = -r. (8)

Для определения момента действия жидкости на несущее тело (6) поступим аналогично процедуре, указанной в работе [2]. В силу малости числа Рейнольдса будем искать указанные моменты с точностью до величины порядка м . Из уравнений (4) выразим компоненты углового ускорения co = ( p , q , r ) с учетом соотношений (8):

p =

[(c - B)qr + I(q°3 - ro2)] (A -1)

[(A - C)pr + I(ro - p°3)]

^q =-- 77 —А------

^- ^Dg 1 ;

^- ^Dg 2 ;

[(B - A)pq+I(po 2- q°i)] (c -1)

^- ^Dg 3 -

(9) Продифференцировав выражения (9), найдем вторые производные компонент угловой скорости. Для краткости запишем вторую производную только одной компоненты:

p = ( A -1 11B - CXqr+qr)+

+ 1 ( qo 3 + qd ₃ - T"O ₂ - rd ₂ )] - pDg 1 - ⁽ )

Подставляя выражения (10) в формулу (5) и оставляя слагаемые, порядок малости которых не больше µ, получим зависимость момента, действующего со стороны жидкости, от производных компонент угловой ско- рости не выше первого порядка.

Выражения (4) и (8) представляют собой динамические уравнения движения свободного гиростата (моменты внешних сил равны нулю), состоящего из несущего тела со сферической полостью, заполненной вязкой жидкостью, и трех свободно вращающихся роторов. Система динамических уравнений (4), (8) замыкается известными кинематическими уравнениями Эйлера.

Приближенное аналитическое решение уравнений движения

Рассмотрим систему двух соосных динамически симметричных тел, в одном из которых находится сферическая полость, заполненная вязкой жидкостью. Внутренний момент, действующий на ротор, отсутствует. Уравнения движения такой системы получаются из уравнений движения системы с тремя роторами и полостью, полученных ранее:

Ap - ( A - C ) qr + Iqo = ^PDs ( Cr + Io ) p , νA

Aq + ( A - C ) pr - Ipo = ^PD—(Cr + Io ) q , νA

I (r + o) + C 2 r = - PDfs (p 2 + q 2 ), ν

I (r* + o ) = 0, где — = [(A - C)r - Io]A-1 - новая переменная.

Систему (14) после интегрирования последнего уравнения и алгебраических преобразований можно привести к виду:

^{p -} sq = ^P1 . D_ ps ^{[ C} 2 s ^- I ^{( r} o ^{+ o} 0 ^)] v A A - C ₂

^{q +} sp = ^p 4 л D^ qs ^{[ C} 2 s ^- I ^{( r} o ^{+ o} 0 ^)]

^v A A ^{- C} 2                   _(|5)

C ρD

Arc;^s =^- v A— ^{( p + q )}

Перейдем к безразмерным величинам и ρD Сω введем малую величину s = — — ²   <<  1:

P - SQ = ePS S - -I - ( R о + X 0 )

_ C 2

Q + SP = eQS S - 1- ( R „ + X о ) _ C

5 = - e

A - C₂ ""c T

S ( P ² + Q ² )

.

p <1> S <0> Q <1> S <1> Q <0>_

= P<0>S<0> [s<0> - IC2-1 (R + X0)], q <1> + s <0> p <1> + s <1> P <0>_

= Q ^<0> S < ⁰ > [ s < ⁰ > - IC 2 ' ( R + X 0 ) ], ,S <1> = - ( A - C ₂ ) 2 C ₂ ^{- 2} S < ⁰ > [ ( P ^<0> ) 2 + ( q < ⁰ > ) 2 ]

где каждая безразмерная величина ( P , Q , R , S , X ) – есть отношение соответствующей размерной к начальной угловой скорости несущего тела ^ 0 = ^p ² + q 2 + r ₀² , например P = p _to 0 ^{- 1} - безразмерная компонента угловой скорости, т = 1ю₀- безразмерный параметр времени. “Точка” здесь обозначает дифференцирование по безразмерному времени.

В системе дифференциальных уравнений (16) присутствует малый параметр е , следовательно, для нахождения приближенного аналитического решения применимы асимптотические методы. Воспользуемся методом Пуанкаре [9]. Согласно методу точное решение системы аппроксимируется своим разложением в ряд по степеням малого параметра: ^            ^            ^

P = 1/Р < i > , Q = UQ < i > , S = ^ e i S < i > . (17) i = 0                   i = 0                   i = 0

В данном случае ограничимся точностью аппроксимации порядка е , то есть оставим в (17) только первые два слагаемых. Подставим разложения (17) в систему (18) и приравняем коэффициенты при одинаковых степенях малого параметра. Получим порождаю-

С учетом порождающего решения последнее уравнение системы (20) запишется следующим образом:

•S        A - C 2 )2 C 2-2 S 0 (p„2 + Q02), а его решение с начальными условиями S <1>(0) = 0:

S < 1 > =- ( A - C 2 ) ² C 2 ^{- 2} S 0 ( P 0 ² + Q 0 ² T . (21)

С учетом (21) первые два уравнения системы (20) образуют систему неоднородных дифференциальных уравнений со специальной правой частью, решение которой при начальных условиях P < 1 > ( 0 ) = 0, Q < 1 > ( 0 ) = 0 легко найти.

Приближенное решение системы (15) для двух компонент примет следующий вид:

P ( t ) = P 0 cos ⁵ 0 1 + q 0 sin ⁵ 0 1 + ^e —^ t "^x ω ₀

cC - ⁽ r + ^ ° )

( p ₀ cos s ₀ 1 + q ₀ sin s ₀ 1 ) -

x   s 0 ^-

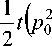
s ⁽ t ) = s 0

, 2 1 A ^{- C} 2 If

⁺ q 0 )          I ⁽ q 0^cos s 0 ^{1 -} p 0^sin s 0 ¹ )

I ^{c 2} )

,

щую систему и систему для поправок.

Порождающая система выглядит следующим образом:

st ε ⁰

ω ₀

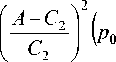
^{+ q} 02 ) .

P < ⁰ >

-

S < ⁰ > Q < ⁰ >

= 0,

Q < ⁰ > + S < ⁰ > P < ⁰ > = 0,

S < ⁰ > = 0,

решение которой:

Аналогично решается задача Дарбу. В кинематические уравнения Эйлера подставляются приближенные решения для компонент угловой скорости, и решение определяется в виде рядов (17). Из-за громоздкости полученные выражения не приводятся. Для проверки правильности полученного прибли-

P < ⁰ > = P ₀ cos S ₀ т + Q ₀ sin S ₀ т ,

^Q < ⁰ > = ^Q 0^{cos S} 0 ^{T - P} 0^{sin S} 0 ^т ,  (₁₉)

S < ⁰ > = S ₀.

Система для поправок принимает вид:

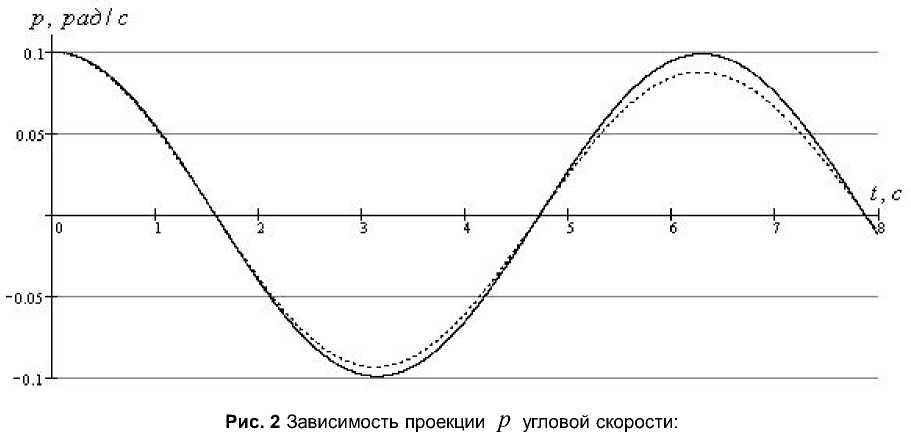
женного аналитического решения сравним его с результатами численного интегрирования системы (14). На рис. 2 показано соответствие численного и аналитического решений для проекции p угловой скорости несущего тела, на рис. 3 – для угла нутации θ . Сплошными линиями изображены аналити-

ческие решения, прерывистыми – численные.

сплошная линия – аналитическое решение, пунктирная – численное

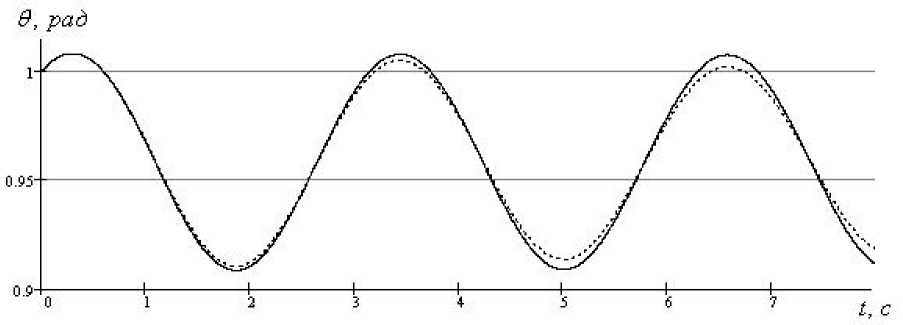
Рис. 3. Зависимость угла нутации θ от времени: сплошная линия – аналитическое решение, пунктирная - численное

По графикам видно, что метод Пуанкаре дает довольно точный результат на небольших промежутках времени. По характеру движения можно сделать вывод о диссипативных свойствах вязкой жидкости. Амплитуда колебаний со временем уменьшается; при отсутствии жидкости такой эффект для свободной системы не наблюдается. Получается, что при движении КА жидкое топливо демпфирует его пространственное движение. Таким образом, в некоторых спутниках можно упростить активную систему демпфирования или вовсе ее не использовать.

Полученные результаты могут быть использованы для исследования движения спутников-гиростатов и КА с двойным вращением, содержащих ЖРД, на пассивных участках их орбитального движения.

Работа выполнена при поддержке Российского фонда фундаментальных исследо- ваний (Грант № 06-08-00325, грант № 06-0100355) и программы поддержки технического образования фонда Alcoa (грант AYF 07003s).