Движение верхнего слоя зерновой смеси на вибрирующей рифленой поверхности

Разделение (сепарирование) сыпучих смесей по разности размеров частиц или по разности плотностей широко используется в различных отраслях промышленности. Например, в пищевой при очистке продовольственного и семенного зерна [1–18], на горнообогатительных предприятиях при отделении руды от пустой породы и т. д. Большой вклад в развитие вибрационного сепарирование зернопродуктов внесли В.В. Гортинский, А.Б. Демский, М.А. Борискин, В.Ф. Веденев и еще ряд преподавателей кафедры «Теории машин и механизмов» Московского государственного университета пищевых производств. При зер-нопереработке сепарирование осуществляется в основном с целью очистки зерна от легких и тяжелых примесей, крупных и мелких примесей, от неполноценных зерен, от семян сорных растений. При этом часто используют очистительные машины с плоскими ситами, совершающими колебательные движения с целью повышения эффективности процесса разделения смеси, для увеличения производительности машин, а также качества разделения. При этом значительное влияние на процесс оказывает конструкция рабочих органов и их кинематические параметры.

Заметим, что непосредственно сепарирование (разделение) происходит в ограниченной по габаритам зоне, за ограниченное время: у ситовых машин над поверхностью перфорированного сита; у воздушных сепараторов в объеме, где происходит контакт ниспадающего слоя зерна, подаваемого часто вибрационным питателем, и восходящего потока очищенного воздуха. Неблагоприятные условия для осуществления сепарирования возникают в том случае, когда примеси и чистое зерно распределены равномерно. Было бы целесообразно иметь большую часть мелких примесей ближе к ситу (при ситовом разделении), а легких примесей – в верхней части слоя, подаваемого в воздушный сепаратор. Таким образом, слой сыпучей зерновой смеси должен проходить предварительную подготовку к участию в процессе, что может быть оценено с помощью анализа кинематических параметров частиц зернового потока, что и является целью данного исследования.

Основное отличие описанного ниже рабочего органа заключается в том, что наклонной рабочей поверхности с рифлями задается вибрационное перемещение перпендикулярное линии наибольшего ската, т.е. перпендикулярно рифлям. Рифли способствуют более качественному разделению зернового потока по массе и размеру зерна за время его движения от начала до окончания поверхности. Положительным результатом данного процесса можно считать более интенсивное всплывание легких частиц.

Описание рабочего органа и процесса вибрационного перемещения зерновой смеси

Плоская рабочая поверхность 1 (рисуно к 1) , наклонённая к горизонтали под углом α , совершает поступательные гармонические колебания по прямой, образующей с линией наибольшего ската поверхности угол, равный 90⁰ . Ранее была опубликована работа [3], в которой этот угол был менее 90⁰ . На рабочей поверхности на некотором расстоянии друг от друга расположены рифли 2, которые выполнены в виде прямолинейных пластин. Рифли установлены параллельно друг другу вдоль линии наибольшего ската рабочей поверхности. Зерновая смесь равномерно поступает на приёмный участок рабочей поверхности, расположенный у торцевой стенки 3. Зерновая смесь под действием колебаний образует на рабочей поверхности поток постоянной толщины, непрерывно движущийся от приёмного участка к противоположному схо-довому участку поверхности. Толщина зернового потока больше высоты рифлей.

Частицы зерновой смеси, расположенные на различных расстояниях от рабочей (опорной) поверхности, имеют различия в движении вследствие неодинаковых условий связи с окружающими частицами и опорной поверхностью. Наименьшей подвижностью обладают частицы нижнего слоя зернового потока, заполняющие пространство между рифлями опорной поверхности.

Нижний слой зернового потока совершает колебания вместе с рабочей поверхностью. Верхний слой связан с нижним только силами трения, причем коэффициент сопротивления сдвигу слоёв уменьшается по мере приближения к верхней (свободной) поверхности зернового потока. Это обусловливает интенсивное послойное движение сыпучего тела и сопутствующее ему самосортирование, которое заключается во всплывании в верхние слои частиц меньшей плотности и большего размера и в погружении в нижние слои зернового потока частиц большей плотности и меньшего размера.

Расположение рифлей перпендикулярно направлению колебаний означает, что нижний слой зернового потока неподвижен относительно поверхности в направлении её колебаний. Таким образом, на рабочей поверхности созданы условия для повышения интенсивности послойного движения зернового потока.

Интенсивность послойного движения сыпучего тела оценивают степенью различия скоростей верхнего и нижнего слоёв потока. Скорость нижнего слоя в направлении колебаний равна нулю. Так как эффективность процесса само-сортирования находится в прямой зависимости от интенсивности послойного движения зерновой смеси, то это означает, что на рабочей поверхности созданы наиболее благоприятные условия для протекания процесса самосортирования.

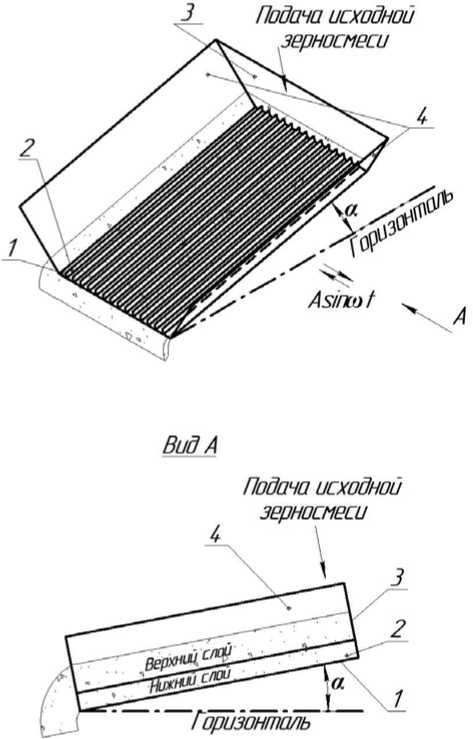
Рисунок 1. Схема рабочего органа и потока сыпучего тела на вибрирующей поверхности при непрерывной подаче исходной зерносмеси

Figure 1. The scheme of the working body and the flow of the bulk body on the vibrating surface with a continuous supply of the initial grain mixture

При колебаниях рабочего органа частицам сыпучего тела от ограничивающих его поверхностей передаются силовые импульсы, которые должны обеспечивать выполнение следующих условий. Во-первых, транспортирование зерновой смеси вдоль рабочей поверхности. Во-вторых, одинаковую на всей площади опорной поверхности интенсивность самосор-тирования зерновой смеси. Выполнение этих условий зависит от величины и направления силовых импульсов.

При осуществлении процессов сепарирования угол α наклона рабочей поверхности к горизонтали должен быть выбран таким, чтобы рабочая поверхность была самотормозящей. Следовательно, должно быть обеспечено направленное в среднем движение (транспортирование) зерновой смеси вдоль рабочей поверхности.

Верхний слой зернового потока совершает движение относительно поверхности под действием двух взаимно перпендикулярных сил: силы инерции переносного движения и составляющей силы тяжести (скатывающей силы), направленной вдоль линии наибольшего ската поверхности. При этом частицы верхнего слоя совершают сложное движение, которое может быть представлено состоящим из движений в двух взаимно перпендикулярных направлениях: «быстрое» колебательное движение относительно линии наибольшего ската и «медленное» движение вдоль линии наибольшего ската.

Для описания вибрационного перемещения зерновой смеси на предлагаемой опорной поверхности рассмотрим, как это сделано в работах [2, 3], двуслойную модель, в которую внесем изменения, обусловленные наличием на опорной поверхности рифлей в виде прямолинейных пластин. Будем считать верхний слой материальной точкой массой m _В , которая связана силами сухого трения с нижним слоем, совершающим колебания вместе с рабочим органом. Следовательно, при исследовании движения верхнего слоя зернового потока будем рассматривать движение материальной точки на наклонной плоскости, совершающей горизонтальные гармонические колебания в направлении, перпендикулярном линии наибольшего ската. При исследовании движения нижнего слоя рассмотрим элемент объёма между смежными рифлями, считая его материальной точкой, которая движется между смежными рифлями без образования зазоров и, следовательно, без ударов о боковые поверхности рифлей. При этом вследствие колебаний рабочего органа материальная частица имеет попеременно силовой контакт с боковой поверхностью то одной рифли, то другой.

Результаты и обсуждение

Движение верхнего слоя

Сложное движение материальной частицы рассмотрим как сумму переносного (вместе с рабочей поверхностью) и относительного (относительно поверхности) в системе координат xyz , жестко связанной с рабочим органом. Оси системы координат расположены следующим образом: ось x направлена вдоль рифлей

(пластин); ось y – перпендикулярно пластинам (перпендикулярно линии наибольшего ската поверхности); ось z – перпендикулярно плоскости рабочей поверхности (рисунок 2) .

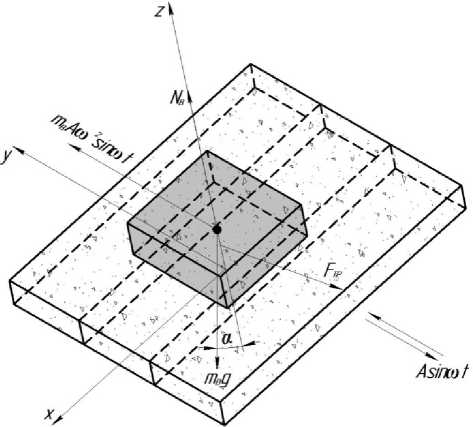
Рисунок 2. Схема сил, действующих на частицу в относительном движении

Figure 2. Scheme of forces acting on a particle in relative motion

Рабочая поверхность совершает горизонтальные гармонические колебания по закону у = A sin rot y = Arocos rot >, y = - Aro2 sin rot где A uro - амплитуда и частота колебаний рабочей поверхности.

На рисунке 2 представлена схема сил, действующих на частицу массой m_B : P B = m B A ro ² sin ro t - сила инерции переносного движения; m_Bg – сила тяжести частицы; N_B – нормальная реакция нижнего слоя; F _ТР – сила трения о нижний слой, совершающий колебания вместе с рабочей поверхностью.

Сила трения F _ТР направлена против относительной скорости V B _- H - верхнего слоя относительно нижнего и образует с осью у угол v .

Условие движения материальной частицы относительно рабочей поверхности имеет вид

( m B A ro ² sin ro t ) + ( m B g sin a ) 2 >  F- ТР . (1)

Дифференциальные уравнения относительного движения частицы в проекциях на оси координат для случая скольжения частицы в положительном направлении оси y имеют вид mBx = mBg sin a - Ftp sin v ; (2)

m B у = m B A ro ² sin ro t - F _tp cos v signy ; (3)

m B Z = - m B g cos a + N B . (4)

В рассматриваемом случае движение частицы вдоль оси x возможно только в положительном направлении. Знак проекции силы трения F _ТР на ось x не зависит от направления скольжения частицы вдоль оси y . При скольжении частицы вдоль оси y имеет место симметрия движущих сил и сил сопротивления относительному движению частицы.

Так как движение частицы происходит без подбрасывания, то z = const и Z = 0, из уравнения (4) получим выражение силы нормального давления:

N B = m B g cos a .

Следовательно,

^F tp = ^N B f= = m B gf c ^{cos a} , ⁽⁵⁾ где f_c – коэффициент сопротивления сдвигу верхнего слоя относительно нижнего.

Преобразуем неравенство (1) и подставим в него выражение силы трения F _ТР из уравнения (5), получим

( m B A ro ² sin ro t ) + ( m B g sin a ) 2 > ( m B gf c cos a ) ². (6)

Первое слагаемое неравенства (6) является переменной величиной, зависящей от времени. Максимальное значение по абсолютной величине это слагаемое принимает при |sin ro t | = 1. Следовательно, угол v , который сила трения F _ТР образует с осью y , является переменной величиной, зависящей от величины силы инерции переносного движения. Максимальное значение угол v принимает в мгновение начала относительного движения частицы. Из неравенства (6) следует, что условие начала относительного движения частицы может быть представлено в виде

( m B A ro ² sin 5 ) = ( m m B gf c cos a ) 2 - ( m B g sin a ) 2 , где 5 = ro t - фазовый угол, аналог безразмерного времени [11].

Тогда минимальное значение силы Р_В инерции переносного движения, при котором частица может начинать относительное движение, имеет вид

( Р В ) min = m B g ( ^f= ^{cos a} ) ^{2 -} sin^{2 a} .

Минимальное и максимальное значения угла v могут быть определены по формулам

v max

■ sin а

= arcsin--------, f cos а c vmin = arctg

g sin а A to²

Анализ приведенных формул позволил сделать следующие выводы. Максимальное значение угла v не зависит от кинематических параметров (амплитуда и частота) колебаний рабочей поверхности, а зависит от угла а наклона поверхности к горизонтали и от коэффициента f_c трения скольжения верхнего слоя относительно нижнего. Минимальное значение угла v зависит от амплитуды и частоты колебаний рабочей поверхности и от угла а её наклона к горизонтали. Поскольку угол v изменяется в достаточно узком диапазоне его значений, будем считать угол v постоянным и примем его значение как среднее максимального и минимального значений.

Преобразуя (2) и (3) с учетом (5) получаем, x = g ■( sin а - fc cos аsinv)

и

( g co cos а cos v )

y = Ato2 ■ sin 5 + —-----:----- .(8)

V           Ato)

В уравнении (8) верхний знак в выражении, стоящем в круглых скобках, соответствует скольжению частицы в положительном направлении оси y , нижний знак – в отрицательном.

Обозначим

7 = ₊ Sf c cos а cos v ± "      A to ^т

Тогда уравнение (8) приводим к виду y = A to ² ■ ( sin 5 - Z ± ) .         (10)

В (9) и (10) верхние индексы и знаки относятся к случаю скольжения частицы в положительном направлении оси y ( y >  0 ) , а нижние индексы и знаки – к случаю скольжения в отрицательном направлении оси y ( y <  0 ) .

Обозначим фазовые углы 5 , при которых начинается относительное скольжение частицы в положительном и отрицательном направлениях оси y , 5 _{1 +} и 5 1 - , а фазовые углы окончания этих скольжений 5^ и 5 • 2 +       2 —

Скольжение частицы в положительном направлении оси y может начаться, если y > 0, то есть при sin 51+ > Z+, где Z+ - безразмерный параметр сопротивления относительному движению частицы в положительном направлении оси y . Скольжение частицы в отрицательном направлении может начаться, если y < 0, то есть при sin 51— < Z—.

Как видно из формулы (9), в рассматриваемом случае вибрационного перемещения имеет место равенство Z ₊ = | Z _— | . Это является следствием того, что, как отмечено выше, при скольжении частицы вдоль оси y имеет место симметрия движущих сил и сил сопротивления относительному скольжению.

Как установлено в работах [10, 11], при таких условиях вибрационного перемещения частица может совершать движение относительно колеблющейся поверхности в двух режимах. Согласно принятой в этих работах терминологии это режим 1 и режим 2. Режим 1 – двустороннее скольжение частицы с двумя паузами. Режим 2 – двустороннее скольжение частицы без пауз (с двумя мгновенными остановками).

В сепарирующих машинах из перечисленных выше режимов целесообразно обеспечивать движение частиц зерновой смеси в режиме 2. Этот режим обеспечивает наиболее рациональное использование времени пребывания сепарируемой зерносмеси на рабочей поверхности, так как процесс самосортирования происходит эффективно при относительном движении слоёв зерновой смеси.

Для определения зависимости скорости частицы при её скольжении в положительном направлении оси y проинтегрируем уравнение (10) в пределах от y = 0 до текущего значения скорости y >  0 и от 5 _{1 +} до текущего значения фазового угла 5 . Зависимость скорости имеет вид y ( 5 ) = A to -[ ( cos 5 _{1 +} — cos 5 ) — Z ₊ ^ ( 5 — 5 _{1 +} ) ] .(11)

Правая часть уравнения обращается в ноль в мгновение прекращения скольжения частицы в положительном направлении оси y , то есть при 5 = 52+. Поэтому после подстановки 5 = 52+ в уравнение (11) имеем cos 51+— cos 52+= Z+\52+- 51+) . (12)

Проведем аналогичные преобразования при скольжении в отрицательном направлении, получим cos 51—— cos 52—= Z—\52—- 51—). (13)

Начало движения частицы в каждом из направлений совпадает по времени и фазовому углу с окончанием движения в противоположном направлении, то есть должно выполняться условие

У + ( 5 ) = A

( cos ⁵ 1 + ^- Z - ⁵ 1 + )( ^{5 - 5} 1 + )

5 ² -

- ( sin 5 - sin 5 _{1 +}) - Z ₊-----

= § 2 + = 51.

.

+ 2 n

Аналогично определим зависимость перемещения в отрицательном направлении оси y

Подставим значения фазовых углов 51- и 52- из системы уравнений (14) в уравнение (13) и после преобразований получим cos 51+ - cos 52+ = Z- ■ (52+ - 51+ - 2п). (15)

Из уравнения (12) и (15), имея в виду, что Z - = - Z ₊ , получим

52+ - 51+ = П , аналогично

§ - 5 = п .

2 -     1 -

Следовательно, при установившемся движении частицы в режиме 2 при выполнении условия Z ₊ = | Z _| фазовые углы начала и окончания скольжения в каждом из направлений отличаются друг от друга на п .

Максимальное значение параметра Z ₊ = ( Z ₊ ) _2max, при котором частица совершает движение относительно рабочей поверхности в режиме 2, равно

(ZA = , 2    . = 0,537.

+ /2max

V 4 + n

Аналогично имеем (Z )    =- 0,537.

^- /2min ’

Аналитические выражения для определения фазовых углов 51+ и 52+ получены в виде х П

§ 1 + = 2

• ■ nZ. arcsin — ⁺ ;

• 5.    = --arcsin — + .

„    3 п . nZ

^{2 +}     2            2

Следующим этапом решения рассматриваемой задачи вибрационного перемещения является определение траектории частицы при её движении относительно поверхности.

Для определения зависимости перемещения частицы в положительном направлении оси y про- интегрируем уравнение (11) в пределах от 51+ до текущего значения фазового угла 5 < 52+ и от у = 0 до текущего значения перемещения у+ > 0.

dy

При интегрировании имеем в виду, что у = -^-,

„    ,    . tody „ о = tot и у =----. Получаем d5

У - ( 5 ) = A

( cos 5 1 - + Z Х)( 5 - 5 1 - )

, . .    . . s _ 5 ² -

- ( sin 5 - sin 5 1 - ) - Z-----

. (17)

Полные перемещения частицы в положительном у ₊ и в отрицательном у _ направлениях оси y получим, подставив в уравнение (16) 5 = 5 _{2 +} , а в уравнение (17) 5 = 5 2 -

Для определения зависимости скорости частицы вдоль оси x проинтегрируем уравнение (7) в пределах от 5 _{1 +} до текущего значения фазового угла 5 <  2 п + 5 _{1 +} и от 5с = 0 до текущего значения скорости Х с >  0 :

x ( 5 ) = — ( sin а - f c cos a sin v )( 5 - 5 _{1 +} ) . (18) to

Для определения зависимости перемещения частицы вдоль оси x проинтегрируем уравнение (18) в тех же пределах x (5 ) = —L to

-(sinа -fc cosasinv)51+ (5 -51+) + a               52 -5+

+ (sin a - f c cos a sin v )---^

Для определения полного перемещения частицы вдоль оси x подставим в уравнение (17) 5 = 2 п + 5 _{1 +} , получим

2n2g z .                   . x x+ = —— ■ (sin a - fc cos a sin v).

to

Средняя скорость частицы вдоль оси x определяется по формуле x to ng (sin a - fc cos asinv)

^Vcp =     =------------------------ .

2 n              to

При построении траектории частицы верхнего слоя относительно рабочей поверхности вычисляем её координаты y и x при одинаковых текущих значениях фазового угла 5 , лежащих в интервале значений, соответствующих интервалам относительного движения частицы. При скольжении частицы относительно поверхности в режиме 2 координату y вычисляем по уравнениям (16) и (17). В уравнении (16) текущее значение фазового угла изменяется в интервале от 5 _{1 +} до 5 _{2 +} , в уравнении (17) - от 5 1 - до 5 2 - . Координату x вычисляем по уравнению (19). При этом текущее значение фазового угла изменяется в интервале от 5 _{1 +} до 5 2 - .

Заключение

Рассмотрена модель двуслойного вибрационного перемещения зернового потока по поверхности с рифлями в виде прямоугольных пластин, расположенных параллельно сходу зерна. При этом впервые в вибрационном сепараторе колебания рабочей поверхности направлены перпендикулярно линии наибольшего ската.

Показано, что верхний слой зернового потока, расположенный над рифлями, совершает сложное движение, состоящее из двух движений во взаимно перпендикулярных направлениях: «быстрое» колебательное движение относительно линии наибольшего ската и «медленное» движение вдоль линии наибольшего ската.