Двойственная задача к эколого-экономической межотраслевой балансовой модели с нелинейной зависимостью и монотонно разложимым оператором

DOI:

Citation. Pavlova M.N., Bednaya T.A., Borisova A.A. Dual Task for the Ecological and Economic Inter-Industry Balance Model with Non-Linear Dependence and Monotonously Decomposable Operator. Vestnik Volgogradskogo gosudarstvennogo universiteta. Seriya 3, Ekonomika. Ekologiya [Science Journal of Volgograd State University. Global Economic System], 2018, vol. 20, no. 3, pp. 42-49. (in Russian). DOI:

Цитирование. Павлова М. Н., Бедная Т. А., Борисова А. А. Двойственная задача к эколого-экономической межотраслевой балансовой модели с нелинейной зависимостью и монотонно разложимым оператором // Вестник Волгоградского государственного университета. Серия 3, Экономика. Экология. – 2018. – Т. 20, № 3. – С. 42–49. – DOI:

Известная в литературе [1] двойственная задача, построенная к линейной экономической модели, носит название модели равновесных цен. Эта модель позволяет прогнозировать цены на продукцию отраслей при известных значениях величин норм добавленной стоимости. Кроме того, с ее помощью прогнозируют изменение цен и инфляцию, являющиеся следствием изменения цены в одной из отраслей.

Больший интерес представляют модели с непрерывным временем. Построенная двойственная модель с непрерывным временем представляет собой систему нелинейных уравнений. Поскольку цены на продукцию не могут принимать отрицательные решения, то решения этих моделей должны быть неотрицательны. Поэтому нахождение условий, при которых модель будет разрешима и при этом иметь неотрицательное решение, является основной задачей. Затраты на выделение вредных отходов и их переработку влекут за собой появление в системе уравнений отрицательных величин. В результате исследуются системы, которые имеют неотрицательные решения при наличии отрицательных заданных параметров.

Ввиду большой отраслевой номенклатуры системы уравнений имеют очень большой порядок, что приводит к большой вычислительной сложности. Поэтому нахождение точного решения нелинейной модели межотраслевого баланса представляется крайне затруднительной задачей. Существенно облегчить эту задачу позволяет нахождение оценок неизвестного решения.

1. Двойственная модель для случая с непрерывным временем

Модель с непрерывным временем, в которой учитывается выделение и переработка вредных отходов и внесение инвестиций на развитие производства:

x ⁽ t ) = A i x ⁽ t ) + ( A i⁽2) — Al² ) y ⁽ t ) +

+ R ^dx(t )+f/?(i)   /?(2)'l dy ⁽ tt)

⁺ B11~T" ⁺ ( B 12 — B 12 Г-ГТ+ f 1 ⁽ t), dt                dt

(!-°)

y (t) = A21 x (t) + A12 y (t) + B21 dx^ + dt dy(t)

⁺ B 22   , — ^f 2^{( t} )

I dt

x ( t ) >  0, y ( t ) >  0, dx^ >  0, dy^ >  0, t e [0; h ]. dt dt

Перейдем от модели с непрерывным временем к модели с дискретным временем. Как известно, при достаточно малых значениях h dxt) «lim x+h - x dyt) «lim y+h - y dt      h ^0     h - dt h '0 h и модель примет вид

• ^X t + h = A 11 x t + h + ( An ^- An ) y t + h ⁺

I D x t + h ^xt . ( n(1) р(2Л y t + h y t . г

• ⁺    B 11 h ^{+ (} B 12 - B 12 )          ⁺ f^- + ^{h -}

• ‘                                 x,^ - x,

• *    t + h = A 21 x t + h ⁺ A 22 y t + h ⁺ B 21    j ⁺

h y,+h - y, f

• ⁺    B 22 h^f 2- 1 + h .

x t + h >  ^0- У, + h >  ^0- x t >  0, y, >  0.

Положим h = 1, где под единицей подразумевается отчетный период,

• (1)        (2)                      (1)         (2)

A 12 ⁽ A 12 A 12 ^{) -} B 12 ⁽ B 12 B 12 ^{) -}

• g 1 = - B 11 x t – B 12 y t + f 1, t +1 , g 2 =

= B21 xt +B22 yt + f2,t+1, тогда имеем

' х. + 1 = ^{( А}П ^{+ B} 11 ) х. + 1 ^{+ (} A 12 ⁺ B 12 ) у, + 1 ⁺ g 1 ,

‘ yl + 1 = ⁽ A 21 ^{+ В} 21 ) ^Xl + 1 ^{+ (} A 22 ^{+ В} 22 ) yl + 1 - g 2 -    (1-¹)

X, + 1 >  0, y , + 1 >  0.

Двойственная модель для (1.1), в которой учтены цены полезных продуктов и плата за выброс в окружающую среду вредных отходов, имеет вид

' p, +1 = ⁽ A _n + B ц) p , +1 + ⁽ A 21 + B 21 ) q , +1 + u 1 ,

‘ q t +1 = ⁽ A 12 ⁺ B 12 ) p t +1 ^{+ (} A 22 ⁺ B 22 ) q t +1 - u 2 -

_Pt+1 > 0-   q,+1 > 0- если рассматривать частный случай модели двойственной к модели Леонтьева – Форда [4], когда Ex = Rn, Ey = Rm, и, следовательно,

EX = Rn - E**, = Rm - p e Rn - q e Rm - u 1 e Rn - u2 e Rm - где Ex*, Ey* – пространства линейных ограниченных функционалов, сопряженные к пространствам *

E = Rn, E = Rm, а C (i,j =1,2) сопряженные опера-x            y                ij торы к операторам Cij = (Aij + Bij).

Будем интерпретировать вектор p как вектор цен полезных продуктов, то есть i -я (1 <  i <  n ) компонента вектора p равна цене одной единицы i -го полезного продукта. Аналогично пусть к -я (1 <  k <  m ) компонента вектора q равна плате за выброс в окружающую среду одной единицы k -го вредного продукта (загрязнения), являющегося побочным результатом производственной деятельности. Вектор и 1 e Rⁿ представляет собой вектор добавленных стоимостей, то есть компонента u ₁ этого вектора указывает стоимость труда, затраченного на создание одной единицы i -го полезного продукта (1 <  i <  n ). Аналогично вектор и ₂ e R^m представляет собой вектор, k -я компонента которого равна уменьшению платы за загрязнение одной единицей k -го вредного продукта окружающей среды, в силу которой сама среда «борется» с загрязнением. Вектор С * p = pC 11 - часть стоимости затрат по созданию единичного вектора полезного продукта, полученная за счет использования в производстве полезных продуктов всех отраслей в соответствующих количествах. Вектор С *, q = qC ₂₁ - часть стоимости затрат при создании единичного вектора полезного продукта, связанная с мероприятиями по охране окружающей среды. Вектор С * p = pC ₁₂ = p ( С ™ - С ₁ ⁽ ₂ ²⁾ ) - часть затрат- направленных на борьбу с загрязнением окружающей среды C ₁ ⁽ ₂ ¹⁾ и переработку отходов C ₁ ⁽ ₂ ²⁾ , равная стоимости затраченных полезных продуктов при уничтожении и переработке единицы вредного продукта. Наконец- СX-qq = qC ₂₂ - часть затрат на борьбу с загрязнением, равная плате за побочный (вредный) результат этой деятельности, связанный с дополнительными выбросами в окружающую среду вредных продуктов при уничтожении единицы этого продукта (например, выброс в воздух вредных соединений при сжигании мусора), то есть создание новых групп вредных продуктов при уничтожении вредных отходов.

В последней модели, аналогично тому, как это было сделано ранее, переходим к непрерывному времени, считая, что единица – это отчетный период.

Введем обозначения u1= s1 – B11pt – B21qt, u2= s2 + B12pt – B22qt, получим p,+h = A» p,+h+ A21 q,+h+

, _D p, + h ^— p, , _D  q, + h ^— q, , „

+ Bi i------;------+ B21-----;-----+ si,,+h’ h            h q,+h =(An — 42))p.+h+ A 22 q,+h+

+ ( B((1) — B(2) ) p ^{+ h} - p ‘ + B_n q ^{+ h} — q — s

I x 12      12 ' h 22 h p+h> 0, q,+h> 0, p t> 0, q,> 0.

Получили двойственную модель для модели (1.0).

p ^{( ,} ) = A ii p ^{( ,} ) ⁺ A 21 q ^{( ,} ) ⁺ dp ( t )        dq ( t )

+ Bi? Л + B 21       + si’ d,         d,

> q ( , ) = ( A n — A n) ) p ( , ) + A 22 q ( , ) +

+ ( b ;?

—

B™ ) dpi! + B^

• ¹² dt ²² dt

p ( , ) >  o, q ( , ) >  0-

—

s ₂ ,

Преобразуем полученную модель. Обозначим:

/ x        fdp ⁽') )

f p(,)) dz_ IT z  V q(t) J’ d, МЙ ’

I d, J

• f si ) A = f Aii A1W 00

• V— s ₂ J ’       ( A i⁽2) A 22 J ( A *²) 0 J ’

B = f B11  B21U 00

(1)                        (2)

V 12    -^22 J \ -^12

C = ( E – A )^-1 B , s = ( E – A )^-1 f .

В этом случае двойственная модель перепишется следующим образом [3]:

p(,) = d С11 p(,)+d С 21 q(,)+ s 1(, X dtdt

(?)( q (C )     7 V12 p (1)     7 V12 p (1) + 7 ^22q (1)   s 2( 1 )- l       d,           d,d,

C j ⁽ p ) = d C j p ^{( ,} ), C j ⁽ q ) = d C j q ^{( ,} ) , ¹ , ^j =1,2 tt

Экономический смысл

Первое уравнение этой модели означает, что цена полезного продукта является справедливой, так как она состоит из стоимости затраченных полезных продуктов (как в процессе производства, так и в процессе борьбы с загрязнением окружающей среды) и добавленной стоимости, то есть стоимости затраченного труда. Второе соотношение модели (1.2) означает, что плата за создание одной единицы загрязнения есть сумма стоимости затраченного на борьбу с загрязнением полезного продукта и стоимости затрат на уничтожение воспроизводимого загрязнения и затрат на утилизацию. При этом назначенная плата за загрязнение является справедливой.

Необходимо выяснить условия, при которых система операторных уравнений (1.2) имеет неотрицательное решение ( p ^*, q ^*) при заданных неотрицательных векторах s 1 >  0, s 2 >  0. Если E – линейное полуупорядоченное пространство с сильно миниэдральным (существует точная верхняя (нижняя) грань ограниченного множества) нормальным (введена норма) конусом K [5, c. 52], операторы C_ij ( i , j = 1, 2) системы (1.2) вполне непрерывные монотонные и удовлетворяют условию Липшица

II Cj(p)— Cj(q )|| ^ kj ||p — q| ^ (i, j = i,2)’ где kij – константа, причем kij таковы, что спектральный радиус r (Q) < 1, где k11 k21 k12 k22

Q =

Тогда система уравнений (1.2) имеет единственное решение p = p^* , q = q^* .

Действительно, пусть убывающие, ограниченные сверху последовательности pn и qn , которые соответственно имеют пределы p и q, и возрастающие, ограниченные снизу последовательности pn и qn , пределы которых p и q удовлетворяют системам или при

' p = С ii⁽ p ) ⁺ С 2i ( q ) ⁺ s I ,

(1)(2)

q = С 12 ( p ) — С 12 ( p ) ⁺ С 2 2 ( q ) — s 2’

(1.2)

' p = С 11 ( p ) ⁺ С 21 С q ) ⁺ s 1 ’

(1)           (2)

iq   С12 (p) С12 (p) + С22 (q)

где C_ij ( p ), C_ij ( q ) i , j = 1, 2 – монотонные операторы.

' p = С ii ( p ) ⁺ С 21 ( q ) ⁺ s i ’

⁽¹⁾fn'l C ⁽²⁾ (                  e ⁽ⁱ-4)

l q = С 12 ( p ) — С 12 ( p ) ⁺ С 22 ( q ) — s 2 -

Оценим норму разности первых уравнений систем (1.3)–(1.4)

I p ^- p\ =ll ^C ii ⁽ p ) ^{+ C} 21⁽ q ) ^{+ 5} 1 ^-

^{- C} _n( p ) ^{- C} 21⁽ q ) ^{- 5} J <

< |C„(p) - с„(p)|| + |C21(q) - C21(q)|| < используя условия Липшица

< ^k 11 | \P ^- Д + ^k 21 | q ^- q|-

Сделаем оценку нормы разности вторых уравнений систем (1.3)–(1.4)

I q — ? ! =

C ^( p ) - C <²⁾ ( p ) + C 22 ( q ) - 5 2 - - C ^( p ) + C <²⁾ ( p ) - C 22 ( q ) + 5 2

<

< Цс^ (p )2 - C12) (p )|+1 JC? (p) - c<2) (p )|+ + ||C22 (q ) - C22 (q)|| < (k1(2) - k122>)||p - p|| + + k22 ||q - q|| = k12\\p - p|| + k221|q - q|, то есть

I P — A = ^k 11| \P — Д ^{+ k} 21| ^ — ^Я |’

Ji q — Я П = ^k 12|| ^P — P l ^{+ k} 22 |i q — ^Я .

Пусть a = ( p - p |,| q - q ) ' , тогда ма неравенств (1.5) запишется в виде

(1.5)

систе-

J p 1 = ^C 11 ( pd ^{+ C} 21 ( q 1 ) ^{+ 5} 1 ,             ₍₁₉₎

_л — C ⁽¹)<-п\_Г⁽²)(-п\\Г (л\—^ ⁽ . ) j q 1 ^C 12 ( ^p 1 ) ^C 12 ( ^p 1 ) ^{+ C} 22 ( q 1 ) ⁵ 2^.

/ p 2 = ^C 11 ( p 2 ) ^{+ C} 21 ( q 2 ) ^{+ 5} 1 , p ⁽¹V_n \ P ⁽²> к _n                    ^(1.10)

^ q 2 ^C 12 ( ^p 2 ) ^C 12 ( ^p 2 ) ^{+ C} 22 ( q 2 ) ⁵ 2^.

Из (1.9) путем вычитания (1.10), учитывая условия Липшица, получим следующее:

I p 1 ^- p 2I = ^C n⁽ p 1 ) ^{+ C} 21⁽ q 1 ) ^{+ 5} 1 ^{- C} n⁽ p 2 ) ^{-- C} 21⁽ q 2 ) ^{- 5} J <  ^k 11I p 1 ^- p 2I ^{+ k} 21 q 1 ^- q 2 .

Аналогично

I q 1 ^- q 21 < ^{( k} 12) ^{- k} 1⁽2²⁾ )| p 1 ^- p 21 ^{+ k} 22 q 1 ^- q 21 < <  ^k 12 p 1 ^- p 2 1^{+ k} 22 q 1 ^- q 2 .

В итоге

J p 1 ^- p 2I <  ^k 11I p 1 ^- p 2I ^{+ k} 21 q 1 ^- q 2^ (1 11) j q 1 ^- q 2| <  ^k 121 p 1 ^- p 2| ^{+ k} 22 q 1 ^- q 2 .    ^.

Если положить a = (p 1 - p21, |q 1 - q2 |У, то система неравенств (1.11) запишется в виде a Q • a, a > 0 . Следовательно [5, c. 73], r (Q) > 1,              (1.12)

где a < Qa, a > 0.

(1.6)

Согласно [5, c. 73] из (1.6)

вытекает

Г     ^k 11         ^k 21 )   Г ^k 11    ^k 21 )

(1)        (2)

V ^k 12 ^{+ k} 12 ^k 22 7 V ^k 12 ^k 22 7

r ( Q ) >  1,

(1.7)

k 11

Q = ^(1)₊^(2) V ^k 12 ^{+ k} 12

k k 22 7

( ^kk

V ^k 12

k ”] ^k 22 7

. (1.8)

Из неравенства (1.7) следует, что в случае, когда a ^ 0 , r ( Q ) >  1, где r ( Q ) - спектральный радиус матрицы Q (1.8). Это вытекает из теоремы об оценке спектрального радиуса положительного оператора по его поведению на фиксированном ненулевом элементе конуса К . Следовательно, если r ( Q ) < 1, то a = 0 , а это значит p = p , q = q .

Убедимся в единственности решения.

Предположим, что существует несколько решений системы (1.2) ( p _1, q ₁) и ( p ₂, q ₂), удовлетворяющих системе (1.2):

Из неравенства (1.12) следует, что в случае, когда a ^ 0 , r ( Q ) >  1, где r ( Q ) - спектральный радиус матрицы Q . Следовательно, если r ( Q ) < 1, то a = 0 , а это значит, что p ₁ = p ₂ , q ₁ = q ₂ , то есть система (1.2) имеет единственное решение.

Таким образом, система уравнений (1.2) имеет на конусном отрезке решение (p* , q*). Причем для этого решения выполняются неравенства u2 < p , p < u 1, v2 < q, q < v 1. (1.13)

Рассмотрим оценки решения. Если конус K ^~ правильный нормален [5, с. 36, 42], операто-

ры С*(i = 1,2 , j = 1,2) вполне непрерывные и монотонные, а также существуют векторы ui ,vi такие, что 0 < u2 < и 1, 0 < v2 < v 1 и выполняются условия и1 > С„(uJ + С2,(v1) + 51,

_<      и 2 <  С _п( и 2 ) + С 2, ( v 2 ) + 5 1 ,

(1) А-С(2Чи v1 > С12 (и 1) С12 (и 2) + С 22 ( Ч) 5 2 , (1-14) О)         fX2)/,.

„ ^v 2 — С 12 ^{( и} 2 ) С 12 ^{( и} 1 ) ⁺ С 22 ^{( v} 2 )   ⁵ 2^-

Тогда система (1.2) имеет единственное решение (p*,q*), причем и2 < р* < ир v2 < _* < v 1.     (1.15)

Cистемы (1.3)–(1.4) с учетом (1.13)– (1.14), в силу непрерывности и монотонности операторов, запишутся:

' p = ^С 11⁽ Р ) ^{+ С} 21^{( _} ) ^{+ 5} 1 <  ^С 11^{( и} 1 ) ^{+ С} 21^{( v} 1 ) ⁺

^{+ 5} 1 <  ^и 1 ,

• ■ _ = С 1⁽2) ( р ) - С 1⁽2²⁾ ( Р ) + С 22 ( _ ) - 5 2 <  С ^С и 1 ) -

• - С1(22)(и2) + С22(v1) - 52 < v1.
2. Двусторонние оценки решения двойственной балансовой модели

' p = ^С 11 ^{( р} ) ^{+ С} 21^{( _} ) ^{+ 5} 1 >  ^С 11^{( и} 2 ) ^{+ С} 21^{( v} 2 ) ⁺

^{+ 5} 1 >  ^и 2 ,

(1V                             ^Г^1)^/

^_ С 12 ⁽ p ) С 12 ⁽ p ) ⁺ С 22^{( _} ) ⁵ 2 >  С 12 ^{( и} 2 ) ⁺

+ С^Чи1) + С22(v2) - 52 > v2- и 2 < р , p < и 1, v 2 < _, q < v 1-

Так как было установлено, что р = р , _ = _ , то и ₂ <  р <  и ₁ , v ₂ <  _ <  v ₁ , что совпадает с неравенствами (1.15).

В общей постановке модель (1.2) можно переписать в виде операторного уравнения с монотонно разложимым оператором С ( z ) = = C ₁( z ) – C ₂( z ) [2]:

z = C ₁ ( z ) – C ₂ ( z ) + s .         (2.1)

Здесь C ₁ ( z ) , C ₂ ( z ) – монотонные операторы.

Операторное уравнение (2.1) целесообразно записать в виде z = (C1 – C2)(z) + s,          (2.2)

где

z =

^р 1 , I _ J

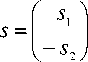
С 1 =

< С

1>

V ^С 12

С 21 1

С 22 J ,

С 1 =

Г 00

с(2)

V С12

По уравнению (2.2) построим новое

уравнение

~ = С (~) + ~,

(2.3)

где z =

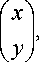
5 =

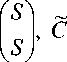
V

C 1

C 2

—

^С 2 А

C 1

У

Элемент ~ z можно рассматривать как элемент нового пространства E = ( E , E ) с нормой ~ z || = || х || + 1| j ||, полуупорядоченного конусом K ~ = ( K , - K ). При этом конус К ~ «наследует» основные св~ойства конуса К [2] .

Оператор C , очевидно, оставляет инва-р~иантным конус K , а это значит, что оператор C положителен относительно K ^~. С помощью изложенной схемы мы фактически можем сводить изучение уравнений с монотонно разложимыми операторами к изучению в~спомо-гательного уравнения с оператором C в но~-вом пространстве E , при этом оператор C является положительным относительно.

Оператор C ₁ является монотонным (то есть из х j <  х 2 => С ( x ₁ ) <  С ( x ₂ )), а С ₂ - анти-тонным (то есть из х ₁ <  х 2 => С ( x 1 ) >  С ( x 2 )) [2].

Пусть оператор C (~ z ) уравнения (2.3) монотонен, непрерывен и вполне непрерывен, удовлетворяет условиям Липшица

||Q^{( и} ) ^- Q^{( v} )|| <  _L. ^и - ^v |( i = 1,2)

и пусть u_{k + 1} = C ₁ ( u_k ) – C ₂ ( v_k ) + s , v_{k + 1} = = C ₁ ( v_k ) – C ₂ ( u_k ) + s , причем u ₀ , v ₀ удовлетворяют неравенствам С ₁ ( и ₀ ) - С ₂ ( v ₀ ) + 5 >  и ₀ , C ₁ ( v ₀ ) – C ₂ ( u ₀ ) + 5 <  v 0 и положим

„ • . ^ик +1 ⁺ m k ^v k +1 „♦ _ ^vk +1 ^{+ т}к^ик +1

ик + 1            1 ,               , vk + 1            1 ,,

1 + m,                1 + m, kk где m, = max{m: и,^, - и, > m(v, - v,^), k             l        k+1       k k кk v, - v,^. > m(и,^, - и,)}.

k       k+1        \ k+1

Тогда имеют место неравенства

u 0 ^- u * ^- u k ^- ... ^- z * ^- ... ^{- v} k ^{- v} * ^{- v} о , (2.⁴⁾

и либо метод сходится за конечное число шагов, либо верна оценка:

Ivk+1 - uk+1l - Х+1 ^L^Vk — uklI, qL – константа Липшица.

Действительно, покажем, что

Рассмотрим норму разности v k _{+ 1} и u k _{+ 1}

1	— ( C ( V k ) — + m, k		C 2 ( u k ) + 5 ) + m k ( C , ( u k ) —	C 2( V k ) + 5 )	—
— r^( C ( u k ) — 1 + m, k			C 2 ( v k ) + 5 ) + m k ( C 1 ( v k )	C 2 ( u k ) + 5	-
-	1 — mk 1 + mk	(I C 1 ( v k ) — C , ( u k )|| + | C 2 ( V k )		— C 2 ( u k ))	-
	-	1 — m k 1 + m k	( q ^l v k — u k\ + q 2 L u k	- v k l ^’

uk+1 - C 1(ukj - C2(vk+1) + 5, а vk+1 - C 1(Vk+1) - C2(uk+1) + 5 .

На основании свойства линейности оператора имеем

^C 1⁽ u k +1 ) — ^C 2^{( V} LD ^{+ 5} — u k +1 =

так как

9 - C 1 ( V k ) — C 1 ( u k )| + C _z( V k ) — C 2 ( u k )| - ^{- (} q 1 l ⁺ q 2 l ) u k ^— v k |.

На основании [2] данное выражение

1 — mt k 1 + mt k

меньше либо равно

1- χ 1 + X

Тогда

_{= r} I u k + 1 ⁺ m k v k + 1

= С ₁

I ^{1 +} m k

—

I v^ + m: U i k+1         k k+1      I r 1V

С I                 I + 5 — u

2           i                                     k + 1

I ^{1 +} m k   J

= .  ¹     <  ^C 1⁽ u k + 1 ⁺ m k v k + 1 ) — ^C 2⁽ v k +1 ⁺ mkuk +1 ) ⁺

• ^{1    +} mk

+ 5 (1 + m, ) — u_. — m,v_ .) = V          k /      k +1         k k +1 /

= r^( C 1 ( U k +1 ) — C 2 ( Vk +1 ) + 5 +

• ^{1    +} m k

⁺ m k ^{( C} 1 ⁽ v k + 1 ) — ^C 2 ⁽ u k +1 ) ^{+ 5} ) — u k + 1 — m k v k + 1 ) =

I v k +1

—

u k +1 II ^-

X — 1X +1

q L\\ v k ^— u k

Таким образом, метод сходится со скоростью геометрической прогрессии [2].

. ¹     (( u k + 2 — u k + 1 ) — m k ( v k + 1 — v k + 2 )) >  ⁹ ,

1 + mk так как (uk+1 — uk) > m(vk — vk+1), а следовательно,

u k +1 ^- C 1⁽ u k +1 ) — C 2⁽ v k +1 ) ^{+ 5} .

Аналогично можно показать, что

V *+1 - C , ( v k +1 ) — C 2 ( u k +1 ) + 5 .

Построение отрезка (2.4) можно рассматривать как один шаг рекуррентного процесса по уточнению двусторонних границ неизвестного решения х^* исходного уравнения. Повторяя этот процесс достаточное число раз, мы в итоге получим метод построения двусторонних приближений, который можно рассматривать как метод ускорения сходимости двусторонних приближений в случае уравнения с монотонно разложимым оператором [2].