Двухчастичный элемент магнитореологического эластомера под действием осциллирующего магнитного поля и переменной механической нагрузки

Среди множества разрабатываемых новых материалов особый интерес привлекают так называемые смарт-материалы, свойства которых могут контролируемо изменяться и подстраиваться под переменные внешние условия. К таким материалам относят и магнитореологические эластомеры (МРЭ) — композиты, состоящие из эластомерной матрицы и намагничивающихся частиц микронных размеров в качестве наполнителя. Особенностью этих материалов является их магниточувствительность: при приложении внешнего магнитного поля частицы внутри композита намагничиваются и, взаимодействуя друг с другом, меняют свое пространственное положение. Это вызывает изменение макроскопических свойств МРЭ (модуля упругости, вязкости, электрической и магнитной проницаемостей, проводимости и других) Перспективным представляется применение МРЭ для создания адаптивных демпферов, микроманипуляторов, клапанов и насосов. В подобных устройствах в ответ на приложенное поле или механическую нагрузку характеристики элемента из МРЭ или его форма должны изменяться в режиме реального времени. Поэтому изучение динамических характеристик МРЭ является важным, о чём свидетельствует достаточно большое число опубликованных по этому направлению экспериментальных работ [1–6].

2.    Двухчастичный элемент

Сложные механизмы взаимодействия компонентов МРЭ, обусловливающие перестройку его внутренней структуры, необходимо изучать на мезоскопическом уровне. При этом матрица и частицы считаются отдельными сплошными средами со своими собственными свойствами, и принимается гипотеза об их контакте на границе раздела фаз.

С этих позиций в настоящей работе рассматривается представительный элемент МРЭ (Рис. 1 а ) — часть композита, включающая пару сферических частиц, демонстрирующий изменение пространственного положения частиц наполнителя в структуре материала. Элемент имеет вид цилиндра, размеры которого подобраны так, что пара частиц с центрами на его оси занимает 30% его геометрического объёма. Центры частиц соединяются вектором l , их радиусы равны a . Контакт частиц с матрицей считается идеальным. Введём цилиндрическую систему координат: ось z направим вертикально вверх по оси вращения элемента, центр координат O разместим в середине вектора l .

Наиболее значимые эффекты демонстрируют мягкие МРЭ с модулем Юнга ~8–30 кПа (см., например, [4]). Вязкоупругость такого композита характеризуется временами релаксации порядка нескольких секунд [7]. Такие времена присущи МРЭ, наполненным карбонильным железом с микрочастицами размером 2–5 мкм, обладающими высокой восприимчивостью порядка 104 и намагниченностью насыщения 1500 кА/м [8]. Отметим, что при определённых условиях нелинейностью как упругих свойств эластомера, так и намагничивания частиц можно пренебречь, по крайней мере, в первом приближении.

Внешнее однородное магнитное поле прикладывается параллельно оси элемента H 0 = ( 0,0, H 0 ) (Рис. 1 а ). В такой конфигурации между намагничивающимися частицами возникают силы притяжения, стремящиеся сблизить их. В то же время в вязкоупругом эластомере появляются силы, сопротивляющиеся их перемещению. При достаточно быстром изменении приложенного магнитного поля смещение частиц внутри матрицы во многом будет обусловливаться вязкими свойствами эластомера. Если же поле изменяется медленно или его величина зафиксирована, то частицы через некоторое время займут в матрице равновесное положение, определяемое балансом между магнитными и упругими силами.

Магнитомеханический отклик исследуемой системы в квазистатическом случае подробно изучался в работах авторов [9–11]. При моделировании учитывались нелинейность и неоднородность намагничивания частиц, а также неоднородность деформирования нелинейно-упругой эластомерной матрицы. Установлено, что при определённом соотношении свойств частиц и матрицы система демонстрирует бистабильное поведение. При циклическом изменении напряжённости приложенного магнитного поля возникает магнитомеханический гистерезис: путь, который частицы проходят при увеличении напряжённости поля, не совпадает с путём при её уменьшении (Рис. 1 б ). Основным параметром, определяющим этот эффект, является Р = ц ₀ M S (с_х , где ц ₀ — магнитная постоянная, M s — намагниченность насыщения, c ₁ — константа упругости модели нелинейно-упругой среды Муни–Ривлина, использовавшейся для описания эластомера.

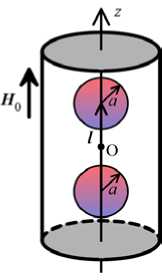
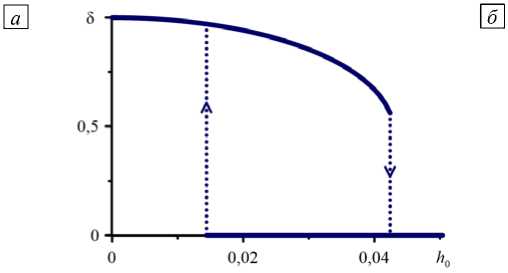
Рис. 1. Мезоскопический двухчастичный элемент ( а ); квазистатический магнитомеханический гистерезис для пары частиц с начальным межцентровым расстоянием l = 3 а и параметром р = 2500 ( б )

Конфигурацию частиц внутри элемента можно охарактеризовать или безразмерным расстоянием между центрами частиц — q, или относительным изменением величины зазора между ними — 5, определяемыми соотношениями:

q = lja    и 5 = (q - 2)/(q0 - 2).

Здесь q ₀ — начальное межцентровое расстояние, q = 2 — предельное значение, отвечающее плотному контакту частиц друг с другом.

На рисунке 1 б представлен пример бистабильного поведения элемента с начальным межцентровым расстоянием q 0 = 1 0 / a = 3 и магнитомеханическим параметром р = 2500, соответствующим МРЭ с намагниченностью насыщения частиц 1500 кА/м и модулем Юнга ~8 кПа. Здесь и далее напряжённость внешнего магнитного поля выражается в безразмерных единицах: h ₀ = H ₀ /M s . Указанные параметры относятся к достаточно мягкому материалу, так что частицы коллапсируют в полях с напряжённостью ~0,04, или в размерных единицах ~60 кА/м (750 Э), далёких от полей насыщения. В полях такой напряжённости для сил магнитного взаимодействия частиц с достаточной степенью точности допустимо использовать линейный закон намагничивания. В дальнейшем для качественного понимания динамических процессов рассмотрение ограничим приближением линейного намагничивания частиц. Их магнитное взаимодействие учтём с помощью решения задачи магнитостатики в виде мультипольного разложения [9]. Такое упрощение нельзя назвать мало реалистичным, поскольку микрочастицы карбонильного железа намагничиваются линейно в полях до нескольких килоэрстед. Несмотря на то, что линейно намагничивающаяся среда не имеет насыщения, сохраним величину M_s как единицу измерения поля.

В случае, когда напряжённость магнитного поля или приложенная нагрузка зависят от времени, кроме магнитных и упругих сил, являющихся потенциальными, движение частиц сопровождается также диссипацией, имеющей два очевидных источника. Во-первых, это взаимодействие вихревых токов, индуцируемых внутри зёрен металла, с приложенным полем (однако этот эффект пренебрежимо мал при малых частотах, не выше нескольких килогерц, используемых в настоящей работе). Во-вторых, — это вязкое трение при движении частиц относительно матрицы. Если движение не слишком быстрое, сила, действующая на частицу, пропорциональна её скорости.

В настоящей работе рассмотрим только малые деформации матрицы, то есть будем считать, что при изменении поля взаимное перемещение частиц 5 происходит так, как показано на рисунке 1 б . В приближении малых деформаций напряжения σ , возникающие в эластомере, могут быть представлены в виде суммы упругой и вязкой составляющих

° = °упр + "вяз = Х11 (e) I + 2Ge + Пe , что соответствует модели Кельвина–Фойгта вязкоупругой среды, в которой вязкий и упругий элементы соединяются параллельно. Здесь e — тензор малых деформаций, X — первый параметр Ламе, G — модуль сдвига, п — вязкость материала.

В рамках линейного закона намагничивания межчастичная магнитная сила может быть описана с помощью аналитического выражения, полученного в [9]. В принятых обозначениях сила запишется следующим образом:

Fмаr = О0 H02 a2 F (q), где безразмерная сила Рмаг зависит от расстояния q между частицами, но не от напряжённости приложенного поля. Так как частицы, по сравнению с матрицей, могут считаться абсолютно твёрдыми телами, введём однородно распределённую объёмную плотность fмаг этой силы таким образом, чтобы она была отлична от нуля только внутри частиц и всегда имела направление вдоль локального магнитного поля. Получим уравнение равновесия . маг .

В рассматриваемых материалах частицы наполнителя микронного размера движутся в полимерной каучукоподрбной матрице. Простые оценки показывают, что инерционное время для такого процесса составляет 10–4 с и менее. Это означает, что в частотном диапазоне, ограниченном несколькими килогерцами, инерцией частиц можно пренебречь [12]. Именно по этой причине инерционное слагаемое в уравнении опущено.

Зададим временную шкалу задачи, используя в качестве единицы измерения время релаксации т R =п/ G согласно модели Кельвина-Фойгта: Г = tj т R . В соответствии с этим введём безразмерную производную тензора малых деформаций по времени и запишем систему уравнений задачи в безразмерном виде:

• V ■ ° + Kh0²f маг = 0,

• ° = — I. (e) I + 2 e + ~e .

3.    Элемент в переменном магнитном поле

G ¹

Здесь напряжение 6 определено как 6 = о/ G , набла-оператор — V = a V , а коэффициент перед безразмерной магнитной силой — к = ц ₀ M S a³ /G . Завершим постановку заданием условия свободной от напряжений боковой поверхности элемента и безразмерного усилия в виде вектора p на его торцах.

Пусть переменное внешнее магнитное поле h0 = hA sin (юt) = hA sin (cot),      ю = ютR с амплитудой hA приложено вдоль оси двухчастичного элемента; здесь ю — безразмерная частота колебаний поля. Частицы являются магнитомягкими и не обладают остаточной намагниченностью. Магнитная сила, возникающая между ними, не зависит от направления приложенного поля и будет осциллировать с удвоенной частотой. То же относится к временно́й зависимости вынужденного изменения межчастичного зазора 5.

Магнитомеханическая задача колебаний в переменном магнитном поле, представленная в предыдущем разделе, решалась в осесимметричной постановке численно методом конечных элементов с помощью программы на языке Python с использованием библиотеки FEniCS [13].

Наиболее интересный случай поведения рассматриваемого мезоскопического элемента — это случай, при котором напряжённость приложенного магнитного поля достаточно велика для того, чтобы спровоцировать коллапс частиц. В течение определённой части цикла колебаний поля, когда напряжённость максимальна, частицы, несмотря на вязкое сопротивление, будут находиться в состоянии кластера, падая друг на друга в начале этого периода и разделяясь в конце. Вследствие существенной нелинейности задачи построить её аналитическое решение не представляется возможным. Единственным способом получения результатов является численное моделирование. Однако следует отметить, что подход, используемый в настоящей работе, не давая представления о подобных режимах, позволяет, тем не менее, приблизиться к их пониманию.

В работе [12] рассмотрены колебания пары магнитомягких частиц, заключённых в эластомер, возбуждаемые переменным (гармоническим) магнитным полем в отсутствие механической нагрузки. Показано, что в достаточно сильном поле возможна динамическая кластеризация: в течение некоторой части цикла частицы находятся в состоянии кластера. При этом мгновенное значение поля перехода в «сжатое» состояние всегда превышает значение поля перехода в квазистатическом гистерезисе. Величина этого превышения возрастает с частотой. Наличие такой зависимости легко объяснить. Чтобы образовать кластер, частицы должны переместиться в матрице на расстояние порядка собственного размера. При наличии вязкого трения со стороны полимера этот процесс требует некоторого конечного времени. Если период поля (пусть даже его амплитуда весьма велика) меньше, чем это необходимое время, коллапс пары произойти не может. В этих условиях частицы реагируют на воздействие поля только малыми колебаниями вокруг исходного положения. Соответствующий такому движению магнитодеформационный цикл, то есть траектория системы на плоскости ( h 2 , 5 ) , замкнут. При снижении частоты колебаний поля до значений, при которых соотношение временных интервалов меняется на обратное, траектория терпит разрыв. Указанные ситуации иллюстрируют сплошные линии на рисунке 2.

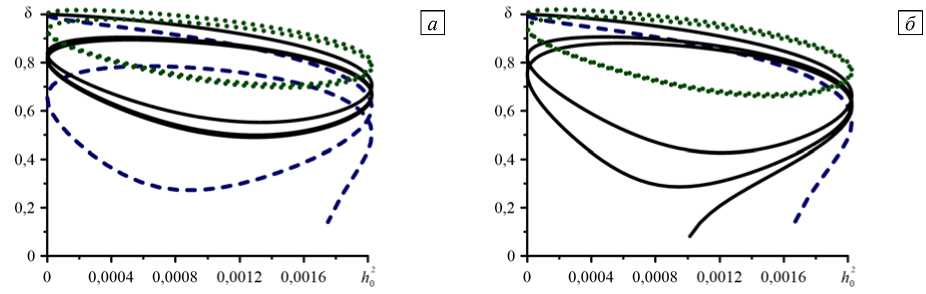
Рис. 2. Установление магнитодеформационного цикла поведения двухчастичного элемента в магнитном поле, осциллирующем с амплитудой 0,045 и частотами 65 0,6 (а) и 0,5 (б) при различных значениях постоянного давления: 0 (сплошная линия); 270 (пунктирная линия); -270 (штриховая линия)

Очевидно, что дополнительная механическая нагрузка может оказывать влияние на поведение частиц, подверженных действию переменного магнитного поля. Так небольшое сжатие ( p <  0) мезоскопического элемента упрощает кластеризацию частиц (Рис. 2 б ), а при чуть более высоких частотах 6 даже устойчивый цикл колебаний частиц может привести их к коллапсу (Рис. 2 а ). Растяжение образца ( p >  0), напротив, затрудняет перемещение частиц навстречу друг другу. Цикл на фазовой диаграмме становится более узким и смещается в область больших 5 , вплоть до полной блокировки коллапса.

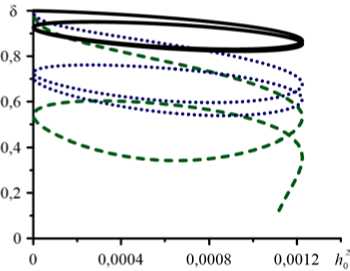
Рис. 3. Установление магнитодеформационного цикла двухчастичного элемента в магнитном поле, осциллирующем с амплитудой 0,035 и частотой 0,75 при значениях постоянного давления: 0 (сплошная линия); - 300 (пунктирная линия); - 500 (штриховая линия)

Более того, как показывает квазистатический случай [11], при существовании в системе с некоторым значением параметра Р магнитомеханического гистерезиса, последний под воздействием внешней механической нагрузки может возникать в поле любой напряжённости. Например, при осцилляциях поля с амплитудой ниже критической, установленной в квазистатическом случае для коллапса, движение частиц будет устойчивым при любых частотах 6 [12]. Однако сжатие двухчастичного элемента давлением определённой величины снижает напряжённость поля, необходимую для кластеризации. На фазовой диаграмме (Рис. 3) видно, что зазор 5 между частицами после пары циклов устремляется к нулю лишь при приложении достаточно большого давления ( p = - 500).

4.    Двухчастичный элемент под действием переменной механической нагрузки

Пусть теперь к торцам рассматриваемого мезоскопического элемента приложено усилие p = ( 0,0, p ) , меняющееся во времени: