Двухфазная фильтрация в трещиновато-пористой среде

Деформация каркаса сильно влияет на течение жидкости и газа в трещиновато-пористой среде. Для построения вычислительной технологии мы опирались на математическую модель фильтрации газовой и жидкой фаз в анизотропных средах, построенную на основе трудов Ван Генухтена ( Van Genuchten):

др Gm (1 - s) ------------ - div

д t

я F др ms дt

- div

IK k^G

Ц G

IK k F

Ц F

GrGGr р (Vp -р g)

рF ('TpF -рFg)

= q^G ;

= q^F ;

р G=рG(pG)=р

G ,0 p^{G ,}

p ⁰ — атмосферное давление;

GV m = m (p ) — пористость (-^n , Vn — объем пор);

s — эффективная влагонасыщенность;

IK — тензор проницаемости, в общем случае полно заполненный;

k G = V1 - s ( 1 - s ² ) — относительная проницаемость для газовой фазы; ц ^G — вязкость газа; q^G — источниковый член в балансе газовой фазы; q^F — источниковый член в балансе жидкости;

рF =рF,0 p-, рF,0 — плотность флюида при атмосферном давлении; p kF = Vs (1 - V1 - s2) — относительная проницаемость для жидкой фазы; цF — вязкость флюида;

p^F = p G ^- p ( s ) ; p c ( s ) = p

d ^{1 -} s²                                        d

- ------ — капиллярное давление; p

—

пороговое давление, причем p“

s р Fg

, где а — параметр, характеризую- a

щий пористую среду.

Для построения численной модели будем использовать итерационноразностный алгоритм и формулы расчета давлений газа, которые подробно расписаны в работе [5]:

„ a p^G , + a p^G , + a p^G , + a p^G , + a n' . + a p^G . + b

, (3)

G             ei  j - 1, k , l         wi  j + 1, k , l         si  j , k - 1, l         n Г j , k + 1, l         bi  j , k , l - 1          ti  j , k , l + 1

p,. k,l =----------------------------------------------------------------------------------------------- a p

Здесь

(a(a (p V) j , k , l                                           j , k , l                     j , k , l

a = a + a + a + a + a. + a, + ------—, b = ------—-----—.       (4)

p ewsnbt

A t               A t

При этом будем иметь

2в G1

__                         j 2                               аe (x+1 -xj-1)(xj -xj-1)’ w    (x+1 -xj-1)(xj+1 -xj) ’

2e g- 1^ц a = 7----------7T2--------7 , a = 7----------77^7,

( y_t + , - y_t - i )( y_t - y_t - i )    " ( y_t + , - y_t - i )( y_t + , - y_t )

2в G -                            2p g+ , a =--------------2----------. a =--------------2

( z, + 1 - z, - 1 )( z , - z , - 1 )     ' ( z , + 1 - z , - 1 )( z , + 1 - z , )

Для упрощения записи у коэффициента в опускаем целые индексы. Значения в в дробной точке определяем через значения в целых точках:

в G +в G - 1

- G - 1

Деформация пористого пласта

Отметим, что предложенная разностная схема обладает большой универсальностью, поскольку позволяет решать задачи в предельно широком диапазоне изменения влагонасыщенности. Опытные зависимости для коэффициентов относительной проницаемости для жидкой фазы, так и для газовой среды имеют нулевые значения при S = 0 и при S = 1. Это приводит к многообразию ситуаций по влиянию окружения на разностное решение в точке. Из-за этого специализированные методы, ориентированные на конкретный тип уравнения, не справляются с решением задачи двухфазной фильтрации. Рассмотрим возникающие ситуации, характерные для плоской задачи фильтрации. В то же время пласт будем считать линейно деформируемой средой, следующей закону Гука. В случае отсутствия влияния массовых сил перемещения точек пористой среды будут зависеть только от коэффициента Пуассона. Этот коэффициент, в свою очередь, будет зависеть от влагонасыщенности пласта. Однако из-за отсутствия данных о влиянии влаги, находящейся в порах, на характер деформации пористого каркаса будем исходить из постоянной величины коэффициента Пуассона. При этом предлагаемая вычислительная технология без труда обобщается на случай переменной величины этого коэффициента. Таким образом, мы включаем в расчет напряжения, которые возникают в пористой среде из-за воздействия слоев, окружающей пласт среды.

Значения этих напряжений напрямую зависят от свойств упругости материала, из которого состоит пласт, а также от величины его деформации. Для решения задачи мы вначале найдем перемещения. Для нахождения компонентов тензора искомых напряжений будем использовать реологическую модель упругого тела .

В декартовых координатах уравнения равновесия в перемещениях выглядят так [8]:

х 1 д0 р

V ² и ++ f = 0, 1 - 2 v д x G

х 1 д0 Р , n

V ² v ++ f = 0, 1 - 2vд у G

x 1 д0 Р , .

V ² w +-- + — f = 0,

1 - 2 v д z G

„ ди д v д w

0 = — + — + —, д x д у д z

где и, v, w — проекции смещения точки; x, у, z — декартовы координаты; р — плотность; fx, fy, fz — проекции массовой силы на оси выбранной сис-E темы координат; 0 — объемная деформация; G = —---- — модуль уп-

2 ( 1 + v )

ругости при сдвиге; v — коэффициент Пуассона; E — модуль Юнга;

, д2 , д2 , д2

V = —7 + —7 + —7 — оператор Лапласа.

д x ² д у ² д z z

В дальнейшем положим, что нагрузки на контактирующие элементы системы настолько велики, что можно пренебречь их собственным весом по сравнению с нагрузками. Электромагнитное воздействие не будем рассматривать, так что, исходя из вышеизложенного,

Подставляя (11) в (8)-(9) и раскрывая оператор Лапласа, получим следующую систему уравнений в перемещениях:

где b =

1 - 2v

, д 2 и д 2 и b —т + —2 д x 2 д у 2	+	д 2 и ТГ + д z
д 2 v д 2 v —7 + b —7 д x 2 д у 2	+	д 2 v 1+ + l д z
д 2 w д 2 w + д x 2 д у 2	д 2 w + b —Г" д z 2
2 - 2 v

•

д ² v д x д у д ² и -----+ д x д у

I ^ ' дx д z

д ² w д x д z д ² w д у д z

'

' дудz

= 0,	(12)
= 0,	(13)
-= 0,	(14)

После того как найдены компоненты перемещений, используя запись тензора Коши, можно определить компоненты деформации. Для нахождения компонентов тензора напряжений можно использовать обобщенный закон Гука.

Разностная схема

Умножая каждое из определяющих уравнений на r ² и аппроксимируя производные в уравнениях (12)-(14) симметричными разностями на неравномерной сетке, получим следующие соотношения:

a s ( u i , j + 1, k - u i , j , k )^- a n ( u jk - u ij - lk ) ⁺ ba w ( u i + 1, j,k ui, j,k )

• ^- ba e ( u i , j , k ^- u i — 1, j , k ) + a ( u i , j , k + i ^- u i , j , k )^{-                                  (15)}

• - at ⁽ ui , j , k - ui , j , k - 1 ) ^- ui , j , k ⁺ s p 1 = ⁰,

bas ( vi, j + 1, k ^- vi, j , k )^- ban ( vi, j , k ^- vi, j - 1, k ) ⁺ aw ( vi + 1, j , k ^- vi, j , k )^-

- a e ( v jk ^- vi - J k ) ⁺ a b ( v jk + 1 ^- v jk ) ^- a t ( vi,j, k ^- v k - 1 ) ^-             (16)

• - bv i J k ⁺ s p 2 = ⁰,

a s ( w i , , + 1, k ^- w J ) ^- a n ( w, j,k ^- w i , j - 1, k ) ⁺ a w ( w + 1, j , k ^- w i , J , k ) ^-

- a e ( w J ^- w i -U k ) ^{+ b}a b ( w i j , k + 1 ^- w i , J , k ) ^-

-bat (wi,j,k - w,j,k-1 ) + sp3 = 0, где

=2    =________2________ e   (x-x-1)(x+1 -x-1), w (x+1 -xi)(x+1 -X-1),

_________2_________ a =_________ 2_________

⁽ y, ^- y j - 1 ⁾⁽ У , + 1 ^- y j - 1 ) , s ⁽ У , + 1 ^- y, ⁾⁽ y j -+ 1 ^- y j - 1 ) ,

2     =_________ 2_________

( zk - z k - 1 )( zk + 1 - z k - 1 ) , ^b   ( z k + 1 - zk )( zk + 1 - z k - 1 ) ,

^{( b    1)(} vi + 1,J + 1, k    vi + 1, j - 1, k    vi- 1,J + 1, k ⁺ v i - 1, j - 1, k )

⁽ x i + 1 ^- x i - 1 ⁾⁽ у , + 1 ^- у , - 1 )

+

^{( b - 1)(} w i + 1, J , k + 1 ^- w i + 1, J , k - 1 ^- w i - 1, J , k + 1 ⁺ w i - 1, J , k - 1 ) ⁽ x i + 1 ^- x i - 1 ⁾⁽ z k + 1 ^- z k - 1 )

S p 2

^{( b    1)(} u i + 1, j + 1, k     u i + 1, j - 1, k     u i - 1, j + 1, k ⁺ u i - 1, j - 1, k )

⁽ x i + 1 ^- x i - 1 ⁾⁽ у , + 1 ^- у , - 1 )

^{( b - 1)(} w i , j + 1, k + 1 ^- w i , j + 1, k - 1 ^- w i , j - 1, k + 1 ⁺ w i , j - 1, k - 1 ) ⁽ y , + 1 ^- y , - 1 ⁾⁽ z k + 1 ^- z k - 1 )

_ ^{( Ь    1)(} ui + 1, j , k + 1     ui + 1, j , k - 1     ui - 1, j , k + 1 ⁺ ui - 1, j , k - 1 )

p ^{3                      (} xi + 1 ^- xi - 1 ⁾⁽ z k + 1 ^- z k - 1 )

⁽ b ^{- 1)(} vi,j + 1, k + 1 ^- v i , j + 1, k - 1 ^- vi,j - 1, k + 1 ⁺ vi,j - 1, k - 1 )

⁽ y j + 1 ^- y j - 1 ⁾⁽ z k + 1 ^- z k - 1 )

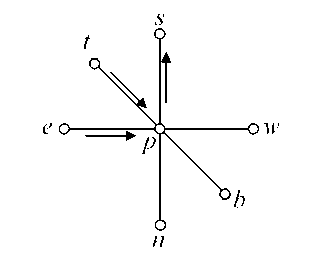
Шаблон разностной сетки (стандартный для регулярной сетки)

Стрелками показаны направления возрастания индексов.

Из разностных уравнений (15) - (17) получаем следующие рекуррентные формулы для определения значений перемещений во внутренних точках:

a e u i , j - 1, k ⁺ a w u i, j + 1, k ⁺ ba n ui - X, j , k ^{+ b}a s u i + 1, j , k ⁺ a t u i, j , k - 1 ⁺ a b u i, j , k + 1 ⁺ s p 1 a p ⁺ a n ( ^Ь " 1 ) ⁺ a s ( ^Ь " 1 )

^ba e v _lJ-1, k ⁺ Kj k ⁺ aW - 1, j , k ⁺ a s V +U , k ⁺ aiv j k - 1 ⁺ a b V j, k + 1 ⁺ s p 2 a p ⁺ a e ( ^{b -} 1 ) ⁺ a w ( ^{b -} 1 )

a e w i , j - 1, k ⁺ a w W , j + 1, k ⁺ a n w i - 1, j , k ⁺ a s w i + 1, j , k ^{+ b}a t W , j , k - 1 ⁺ ba b W, j , k + 1 ⁺ s p 3 ^a p ⁺ a t ( ^{b -} 1 ) ⁺ a b ( ^{b - 1} )

, (26)

которые могут быть использованы при проведении расчетов по методу простой итерации.

Здесь a = a + a + a + a + . p e w n s t b .

Формулы (24)-(26) реализуют решения пространственных уравнений Ляме. Используя их вместе с разностными граничными условиями можно решить все задачи линейной теории упругости в декартовых координатах на неравномерных сетках. Таким образом, с помощью итерационного метода мы решаем задачу упругого деформирования пласта.

Характер влияния ближайшего окружения в стационарных плоских задачах двухфазной фильтрации

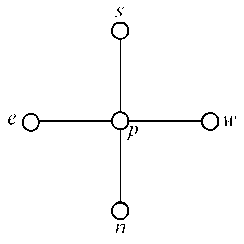
• 1.    Если все a e , a s , a n , a w > 0, задача является эллиптической в точке p .

  

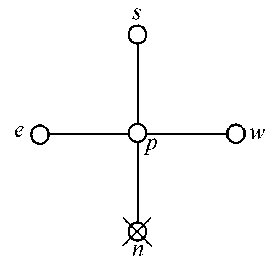
• 2.    Если один из коэффициентов равен нулю, например a n =0, задача параболическая в точке p , причем ось параболичности вертикальная.

  

• 3.    ID-эллиптичность. По одному из направлений отсутствует связанность задачи, в то время как по другому направлению присутствуют двусторонние связи.

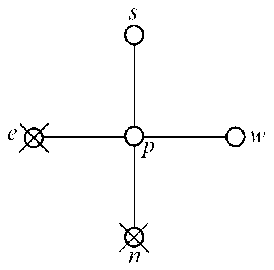
• 4.    Гиперболичность с характеристиками, совпадающими с направлением координатных осей

  

• 5.    Ультрагиперболичность. Характеристики совпадают между собой.

  6. Полное отсутствие влияния окружения. Стабилизация состояния в точке p при продвижении процесса по итерационной оси.

  
  
  

Ор еО----Ор----Cw о п

Результаты расчетов

Описанная ранее вычислительная технология была применена к решению задачи об упругом вдавливании базальтовой плиты в прямоугольную область нефтеносного пласта. Предполагается, что пористая структура пласта, заполненная нефтью, при небольших деформациях ведет себя как упругая среда, подчиняющаяся закону Гука. Квадратный пласт 100 х 100 м 2 и толщиной 4 м в центральной части подвергается действию плиты, которая вдавливается на глубину 0,1 м.

На рис. 1, 2 представлены распределения нормальной и касательной компоненты (одной из двух касательных, которые из-за глобальной симметрии условий деформирования ведут себя схожим образом). Как видно из рис. 1, продавливание породы в центральной части приводит к глобальному выталкиванию всего остального фона и локальному несимметричному выходу материала с левой стороны рисунка. Причем эта асимметрия при использованном направлении перебора внутренних узлов всегда появлялась в одном месте.

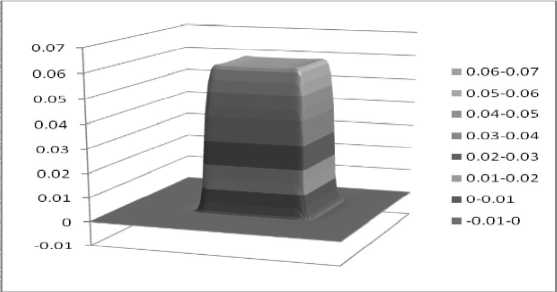
Рис. 1. Нормальная компонента перемещений точек пласта в сечении z = 2 м

Область по вертикали(в направлении z координаты) составляет 4 м, поэтому z = 2 м — это среднее сечение пласта.

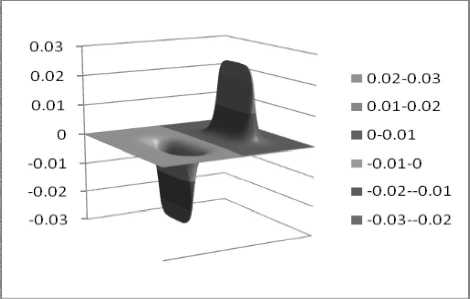
Рис. 2. Касательная компонента перемещений точек пласта в сечении z = 2 м

Рис. 2 иллюстрирует касательную составляющую перемещений в пласте, которая ведет себя асимметричным образом из-за растекания частиц упруго-пористой среды в горизонтальном направлении (перпендикулярном направлению вдавливания).

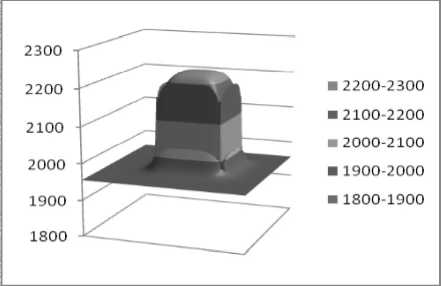
Рис. 3. Изменение плотности при вдавливании квадратной базальтовой области в пласт

Необходимо отметить, что, проявляя свойства несжимаемой среды, материал (каркас и заключенный в нем флюид) деформируется так, что совокупная плотность все-таки изменяется. При этом нами разработана вычислительная технология расчета плотности среды по найденному полю перемещений.

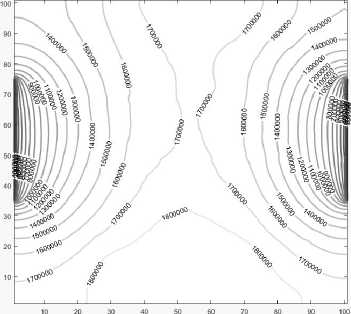
Рис. 4. Изолинии давления газа при вдавливании квадратной базальтовой области по центру.

На западной и восточной стенках находятся окна проницаемости

Из-за разности проницаемостей индивидуальных компонентов в задачах просачивания флюида и выдавливания метана наблюдается относительно быстрое прохождение газовой фазы. Это отражается в том, что даже в стационарных задачах быстрее происходит установление параметров газовой фазы. На рис. 4, 5 показаны распределения давления в среднем сечении пласта в двух формах: в виде изолиний (рис. 4) и поверхности (рис. 5). Почти симметричная форма графиков определяется симметрией в постановке задачи и свидетельствует о завершении процесса установления.

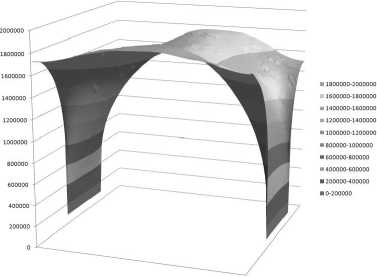
Рис. 5. Поверхность, характеризующая распределение давления газа

Заключение

Таким образом, в настоящей работе разработана и реализована технология решения задач двухфазной фильтрации в деформируемых пластах. Реализация выполнена на примере модели Ван Генухтена для движения флюида и метана в угольных пластах и модели линейно-упругой деформации пористого пласта пористого скелета, содержащего флюид в различной степени насыщенности. Универсальность вычислительной технологии позволяет проводить дальнейшие обобщения математической модели, включая влияние влагонасыщенности на упругие параметры, а также появление новых трещин в пористом каркасе.