Двухпараметрический метод определения коэффициента интенсивности напряжений KI трещиноподобных дефектов методом голографической интерферометрии

Работа посвящена описанию нового метода нахождения коэффициента интенсивности напряжений пластины с трещиноподобным дефектом, использующегося при прогнозировании хрупкого разрушения [1, 2].

В случае тел и дефектов сложной геометрии при попытке получить аналитическую зависимость для вычисления коэффициента K_I методами теории упругости возникают значительные математические трудности. Среди методов натурных экспериментов большое развитие получили методы фотоупругости [3–8], которые позволяют решить широкий круг сложных задач линейной механики разрушения, но сдерживаются недостаточной разработанностью методов.

Можно отметить метод голографической интерферометрии, основанный на использовании картин полос абсолютных разностей хода (АРХ) [4–7, 9, 10]. В работах [5, 8] рассмотрен случай оптически чувствительных пластин с центральной и боковой трещиной. Для них дан обзор и сравнительный анализ фотоупругих методов, используемых при определении величины K .

В линейной механике в рамках теории упругости было принято разлагать компоненты напряжений и перемещений по степеням расстояния до вершины дефекта. В непосредственной близости от конца прямолинейной трещины использовалось «однопараметрическое» представление, т. е. зависящее от коэффициента интенсивности напряжений KI [3]. При таком подходе геометрия тела с трещиной и граничные условия нагружения не учитываются.

Цель статьи - разработка нового метода нахождения коэффициента интенсивности напряжений и номинального напряжения o ox .для пластины с трещиноподобным (эллиптическим) дефектом, основанного на независимом нахождении этих величин. Идея независимости позволяет найти поправочный коэффициент в аналитической формуле для вычисления K . В качестве данных натурного эксперимента используется информация, которая снимается с картин, полученных на основе метода голографической интерферометрии.

Отличие предлагаемого метода заключается в более точном представлении тензора напряжений в окрестности вершины трещиноподобного дефекта. Такое представление позволяет учитывать геометрию дефекта. Вычисленные по предложенному методу значения поправочной функции в формуле для теоретического определения коэффициента интенсивности напряжений оказались выше, чем полученные по ранее использовавшимся методикам. Это, возможно, говорит о недооценке величины коэффициента интенсивности напряжений при использовании ранее предложенных методов. Помимо использования более точных формул для тензора напряжений, подход предусматривает рассмотрение номинального напряжения и коэффициента интенсивности напряжений как независимых параметров. Полный учет геометрии трещины и особенностей нагружения невозможен с аналитической точки зрения, однако данная особенность метода позволяет частично компенсировать упрощения аналитических выражений тензора напряжений. Также данный метод дает возможность определить главные напряжения и интенсивность напряжений в окрестности вершины дефекта.

Описание метода

Для получения значений коэффициента интенсивности напряжений и номинальных напряжений в вершине дефекта выполняются следующие действия. Значения номеров полос совместно с расстояниями от вершины дефекта до середины полосы находятся в результате эксперимента. Далее, с помощью приведенных ниже формул (9) и (10) они преобразуются в значения коэффициента интенсивности напряжений и интенсивность напряжений соответственно. Полученные величины совместно со значениями расстояния до середины полосы аппроксимируются по методу наименьших квадратов или с применением аналогичных методов линейной функцией c_I ( r ). Строгим обоснованием применения линейной аппроксимации авторы пока не располагают. Во всяком случае, в идеальном случае аппроксимирующая зависимость должна быть постоянна (и следовательно, линейна). Таким образом, значения коэффициента интенсивности напряжений и интенсивность напряжений находятся не в вершине трещины, а на некотором расстоянии от неё по оси дефекта. Итоговое значение а ^к получается как предельное значение данной функции в нуле (что следует интерпретировать как вершину дефекта).

Компоненты напряжения при разложении в ряд по степеням r в окрестности вершины трещины с точностью до второго члена при двухосном нагружении трещиноподобного дефекта имеют вид [10]

ст- сх

+

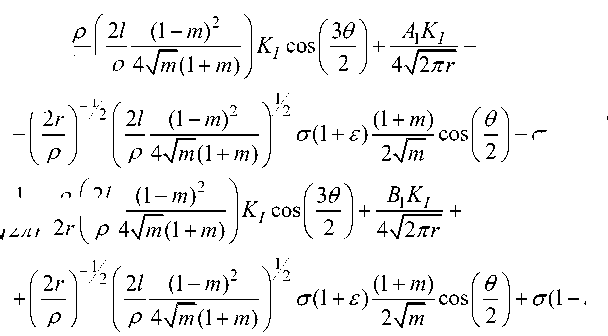
Р

² Г 2 l  (1 - m )²

² Г 2 l  (1 - m )²

K_I cos

K_I cos

..    . (1 + m )      Г 0 )     „    .

^{с (1 + £} ) „ / cos I I — ^{с (1} - ^£

2у m    V 2)

_{л х} (1 + m ) Г 0 ) _{л х} ^{с (1 + £} )    I- cos I I + ^{с (1} - ^£ )

2у m    V 2)

+

1 + m

1 - m

2 m

2 m

Механика

^T xy

1 p Г 2 l (1 - m )²    '

V 2nr 2 r V p 4 4m (1 + m ) _y

K_I sin

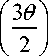
C 1 K I

442nr

2 r

² Г 2 l  (1 - m )²

p

p 4 4m (1 + m )

„    . (1 + m ) .

(j (1 + £ )----j=^-sin

2 m

где с т - номинальное напряжение; £ - параметр двухосности нагружения; m = — ,   , 2 1 -

1 + Jp /l длина трещины, а коэффициенты

A 1 = cos

5 0 I - 17 m ² + 26 m + 15 Г 0

— +------------cos -

8 m

, B 1 = - cos

5 0 I 17 m ² + 38 m - 15

— +--cos

8 m

0 I

2 J ’

C 1 = sin

5 0 I 17 m ² + 6 m - 15 . Г 0 —--------sin -

8 m

•

Коэффициент интенсивности напряжений K для эллиптической трещины ищется по фор муле:

K I

4 m

V (1 + m ) 2

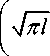
с ( m (1 + к ) + (1 - к )) 2 m

—

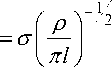
p IV

a

^{1 -} k ^

-

Для случая одноосного растяжения и значений параметра m (зависящего от главных осей эллиптического дефекта), близких к 1, формула (2) упрощается и приобретает вид:

K I / ( ст4П ) « 1 + (1 - m )/2 •

Известно [6], что в плоской фотоупругой модели существуют два семейства полос АРХ N и N2. Номера полос связанны с главными напряжениями 71 и с2 соотношениями Фавра [9]. Для плосконапряженного состояния эти соотношения имеют вид:

N1 = ас1 + bc2; N1 = ас2 + Ьс1, (3) где N2 и a - константы материала исследуемого образца. Эти постоянные определяют на основе модельного эксперимента с пластиной, не содержащей дефекта [7]. Номера полос N[ и N2 в картинах АРХ берутся при различных поляризациях опорного пучка - вертикальной (в = 0°) и горизонтальной (в = 90°) соответственно [4]. Значения констант для рассматриваемого натурно- го эксперимента:

полос           полос a = 0,625------; b = 0,453------•

МПА       МПА

Картины АРХ удобнее всего обрабатывать вдоль оси трещины, так как вдоль нее наблюдается наибольшее количество полос и происходит значительное упрощение формул (1). В этом случае выражения для напряжений [10] приобретают вид: при угле 0 = 0 ° , т_ху = 0 в формулах (1)

DK I p  Г 17 m ² + 30 m - 15 1 K I

42nr 2 r   _v 32 m _y 42nr

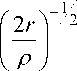
2 3Z                    I - m

D ^Z2 ct (1 + £ ) + < r (1 - £ ) I ----- I ,

V 2 m J

DK, p  Г- 17 m ² + 34 m + 15 1 K   Г 2 r I ^{12 2}Z „           /1 + m I ²

,—L — +-- =I = -I — I    D^{z 2} c(1 + £ ) - c t (1 - £ ) I----I ,

42nr 2 r  V       32 m      J 42nr  V p J                     V 2 m J

(1 + m )

где r - расстояние до вершины трещины, D = —^— •

Из уравнений (1), (3)-(5) для первой картины АРХ выражение

N 1 = K I

D P ( к X 1 ----—( a — b ) — -^

V2 nr 2 r       72

—

a

17 m ² - 30 m — 15

32 m

+ b

— 17 m ² + 34 m + 15

32 m

> —

-т 1

2r i /²    1/       (1 +

_ I    d /2(1 + E )(--=)( a — b ) + (1 — e ) a

V P )            2V m

1 — m 1

2 m 7

—

, i 1 + m 1 b I-----------I

V 2 m 7

,

Для второй картины АРХ соответственно получим

N ₂ = K I <

D P (u A 1

J--- —( b — a ) — —=

V2 nr 2 r       72

-т 1

2 r

—

b

17 m ² - 30 m — 15

32 m

2 U (1 + m)

D /2 (1 + E )(   .   ( b — a ) + (1 — e ) b

— 17 m ² + 34 m + 15

32 m

H

1 — m 1

2 m 7

—

( 1 + m 1 a I —— I

V 2 m )

Считая параметры K I и т независимыми, объединим формулы (6), (7) в систему, решение которой дается формулой:

K = 1

т

где

₊ (1 — E ) 2Плр

2 r_i

D

A =

D /2(1 + e) + (1 — e)----

4 m

17 m ² — 2 m — 15

32 m

' D ^р (t- ^ x 12nr 2 r m

( - ² — b ²) + ( P

V

( b ² — a ²

— 17 m ² + 34 m + 15

32 m

(1 — e)( a + b) ( N — N2)'

(a — b)( n1 + N2) +

—

2 m

^ / A ,  (8)

/ A ,    (9)

D ^/2 (1 + E )( b ² — a ² ) -=^ +

- ( b ² — a ²

17 m ² - 30 m — 15

32 m

\

,

)J 7

где N _{1 i} – номер полосы в i -й точке, расположенной на оси трещины на расстоянии r_i от ее вершины.

Как известно [1, 2], при растяжении пластины с конечными размерами с трещиной коэффициент интенсивности напряжений равен:

K i = т_н па • f i ,

где a_H - номинальные напряжения вдали от трещины; l - полудлина трещины; f₁ - поправочная функция. зависящая от геометрии образца и вида нагружения.

Из выражения (10) получаем:

f. = -Ku , т_н HP

Таким образом, для получения значения поправочной функции f _{1 i} замеряются координаты полос АРХ N_u и N ₂ i на оси трещины ( 0 = 0°), после чего по формулам (8), (11) определяют f_1t . Точность приближенных формул (1) возрастает в окрестности вершины трещины, поэтому полученные значения f_1t экстраполируются в вершину дефекта r = 0. Согласно [5] экспериментальное значение для г мин = ( 3,5 — 4 ) р . Отношение этих величин сохранялось при варьировании радиуса надреза р от 0,1 до 0,25 мм и длины надреза от 3 до 30 мм для пластины шириной 100 мм. Величину r_макс определяли совпадением теоретического по формулам (4), (5) и фактического напряжения [5].

Механика

Также по графикам N и N определяются номера полос в выбранных точках исследуемого сечения, и вычисляются главные напряжения т и ст₂ [7]

aN - bN     aN - bN

•

⁷ 1 =     2   ^2^{2 ;   7} 2 =     2   7,2 1

a - b          a - b

На точность определения главных напряжений с т , , т ₂ влияет точность определения порядков АРХ в исследуемой модели, а также точность тарировочного эксперимента.

Применение метода к результатам натурного эксперимента

Для проверки предложенного метода определения коэффициента KI были использованы данные натурных экспериментов. При проведении экспериментов трещиноподобный надрез имел ширину 0,3 мм и длину 2/ = 13 мм в пластине шириной 2B = 13 мм, толщиной 3,83 мм, выполненной из материала ЭД-20ММГФА. Эксперименты проведены при двух значениях относи тельной длины надреза W = — = 0,13; 0, 3 . Номинальное напряжение для W = 0,3 равно

B

7 H = 3,28МПа, для W = 0,13 равно T H = 4,7 МПа. По обеим картинам N 1 i и N ₂ i по формуле (11) определены значения f 1 i для W = 0,13;0,3 •

Данные натурного эксперимента представляют из себя значения номеров полос и расстояния до центра полосы. Эти значения с помощью формулы (9) преобразуются в значения коэффициента интенсивности напряжений. Полученные значения совместно со значениями расстояния до центра полосы аппроксимируются по методу наименьших квадратов линейной функцией K ( r ) • Применение других методов аппроксимации (метод наименьших модулей, обобщенный метод наименьших модулей) не дало заметных улучшений результатов. Итоговое значение K /кс получается как значение данной функции в нуле (что следует интерпретировать как вершину дефекта).

Для получения интенсивности напряжений выполняются аналогичные процедуры. Значения номеров полос совместно с расстояниями по формуле (10) преобразуются в значения коэффициента интенсивности напряжений. Полученные значения совместно со значениями расстояния до центра полосы аппроксимируются по методу наименьших квадратов линейной функцией 7 ( r ) • Итоговое значение т /кс получается как значение данной функции в нуле (что следует интерпретировать как вершину дефекта).

На рис. 1-2 построены графики для интерполирующей линей функции Kj ( r ) совместно с точками K ) , а на рис. 3-4 графики для линейной аппроксимации 7 I ( r ) и точки т ) (значения интенсивности напряжений в точке r i )• При вычислении т¹ использовались формулы (12) для определения главных напряжений. По значениям K ) построены прямые, приближающие полученные значения и определено значение K ) ^KC . Значения для т¹ выходят на значение т_н при увеличении расстояния. Значения f аппроксимируются прямыми линиями, сходящимися в одну точку.

Экспериментальные средние значения f эксп для двух значений W , полученные по формуле (11), приведены в таблице. Здесь же приведены теоретические значения f , полученные по различным методикам: формула Феддерсена [1, 2], экспериментальные значения, полученные методом фотоупругости по картинам изохром [3], экспериментальные результаты, полученные с помощью метода голографической фотоупругости по картинам АРХ [4].

Дильман В.Л.,                      Двухпараметрический метод определения коэффициента

Рис. 3. Экспериментальные точки с ) , W = 0,3          Рис. 4. Экспериментальные точки C I , W = 0,13

Таблица

W = - B	f = /sec -W 12 Феддерсен [1, 2]	f 1 [3]	f 1 [4]	f 1 (предложенный метод)
0,13	1,01	–	1,00	1.05
0,3	1,06	1,06	1,06	1.08

В случае центрального эллиптического выреза с радиусом кривизны в вершине р = 0,15 мм экспериментальные значения главного напряжения с , определенные методом голографической интерферометрии, согласуются с расчетными значениями с погрешностью 10 %, значения коэффициента интенсивности напряжений K с погрешностью 13 %.

Погрешность составила 2 % по формуле (6) из [4] с результатами натурного эксперимента взятыми из [3]. Расчет велся по формулам с однопараметрическим представлением тензора напряжения на основе коэффициента К_т . Второй член в представлении М. Вильямса с не учитывался. Анализ результатов таблицы показывает, что экспериментальные значения f _{1 i} для W = 0,13 выше значений f = 1,00, приведенных в [4], что произошло за счет добавления слагаемого с в формулах (6)-(7) и последующего их учета в формуле (8). Аналогичные экспериментальные результаты, полученные по картинам изохром методом фотоупругости, приведены в [8] с погрешностью 2–5 % двухпараметрическим методом на основе решения Ирвина.

Некоторые теоретические и экспериментальные исследования по механике разрушения трещиноподобных дефектов в случае двухосного нагружения конструкции приведены в работах [10].

Таким образом, предложенный двухпараметрический метод определения K может быть использован для решения задач линейной механики разрушения с использованием метода голографической интерферометрии по картинам АРХ. Предложенные формулы для расчета K хорошо согласуются с теоретическими результатами.

Механика