Двухсредный автомодельный пограничный слой на плоской пластине

a u a v

— +— = 0        m ax ay    ’               (1)

a u a u

u— + v— = V

ax

ay

g

a2 u a? ’

где X, y - продольная и поперечная декартовы координаты, u, V - соответствующие компоненты скорости, V g - кинематическая вязкость набегающего потока (для определённости будем эту среду называть газом – gas). При необходимости в дальнейшем индекс g будет указывать на принадлежность к набегающему потоку, соответственно среду в узкой плёнке на поверхности обтекаемого тела будем называть жидкостью, и её величины будем писать с индексом l (жидкость –liquid).

Система уравнений (1)–(2) должна быть решена при граничных условиях [3]

y = 0: u = u w ,

a u a y

Mt 2 ^ Q ’

y >^ : u ^ u „ . (4)

Здесь u _м - скорость набегающего потока, u w – скорость потока на границе раздела двух сред (рис. 1), ^ l , Ц _д - динамическая вязкость жидкости и газа соответственно, Q ( x ) - объемный расход жидкости на единицу размаха двухмерного обтекаемого тела, вводимой на твёрдую стенку рассматриваемого сечения x , который зависит от скорости ввода жидкости через пластину v w ( ^X ) ⁽ри^с. 1) ^{(см. [5])}

x

Q ( X ) = j V w ( X ) dx .

Введением переменных Блазиуса [6]

u = u„ f '(n), v = y_

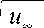
V g X ’

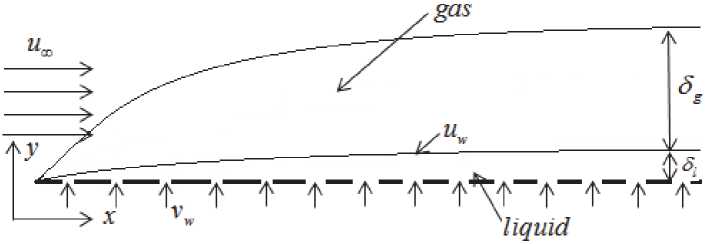
Рис. 1. Схема течения

где f ( у ) - безразмерная функция тока, а f' = df j йу , система уравнений (1)-(2) сводится к одному нелинейному обыкновенному дифференциальному уравнению

2 f "■ ff ' = 0 ,           (6)

что свидетельствует о существовании автомодельных решений уравнений пограничного слоя.

Граничные условия (3) и (4) переходят в сле дующие:

у = 0: f (0) = 0, [f'(0)]2 = ^Qf 10), (7) Д £vgxu у ^те : f '(те)^. 1.          (8)

Для полной автомодельности задачи необхо димо выполнение условия

2 д Q

Л =---- . ^g = const .       (9)

Д ^V_g XU те

В общем случае, когда Л = Л ( X ) , имеет место квазиавтомодельности. Полученные ниже результаты в предположении Л = const могут быть использованы и при приближённом решении аналогичной задачи квазиавтомодельного течения в пограничном слое.

Из (5) и (9) следует, что подвод жидкости через поверхность пластины для обеспечения автомодельности задачи должен происходить с нормальной скоростью вдува v w (см. рис. 1), изменяющейся с координатой x по закону

Д /^gu„

V w ⁽ x ⁾ = ^Л —J— .

Д д V X

Второе граничное условие в (7) запишется как у = 0: [ f ' ( 0 ) ] ² =Л f ' ( 0 ) .       (10)

Краевая задача (6)–(8) и (10) может быть сведена к задаче с начальными условиями. Процедура такого преобразования для уравнения Блазиуса описана в [7], использована в работах автора (первая краткая публикация [8], полное изложение которой появилось лишь в [9]). Систематическое изложение такого преобразования можно найти в [10].

Введение новых переменных f (у )= AF (£), £ = Ау (11) приводит уравнение (6) к тождественной форме

V W          * *

2 F ₊ FF = 0 ,           (12)

где F = dF[d ^ , а постоянная А будет определена позже. Граничные условия (7), (8) и (10) примут вид

£ = 0: F ( 0 ) = 0, [ F ( 0 ) ] ² = A F ( 0 ) ( А = Л/ А ) , (13)

£ ^те : F ( те ) ^ 1/ А ² .       (14)

Из граничного условия (8), формул преобразования (11) и преобразованного граничного условия (14) следует, что постоянная A должна удовлетворять условию

А = V#Н .        (15)

начальные граничные условия можно выбрать равными

£ = 0: F ( 0 ) = 0, F ( 0 ) = 7 я , F ( 0 ) = 1 . (16)

Таким образом, задача решается в следующей последовательности.

Для произвольно выбранного А определяются все условия (16) и выполняется численное интегрирование дифференциального уравнения (12). Оно производится до тех значений £ , при которых F ( £ ) перестаёт изменяться. Это значение F ( £ ) принимается равным F ( те ) . Таким образом, устанавливается значение постоянной A по формуле (15).

После этого с помощью (10) и (13) определяются величины f '(у) = F (£ )/ F (те), у = £ А = V^£, f '(0) = ^FT0^, f "(0) = г—Цк, Л = [f(0)]

F(те) J V ’ [F(те)]^/2         f (0) -

Если необходимо получить функции f (у), f '^п), f "(у) , то они вычисляются ещё од ним интегрированием уже уравнения (6) с извест

-

ными начальными условиями f (0),f '(0) и f '(0) -На рис. 2 – 4 приводятся результаты расче тов F(те) для ряда значений А .

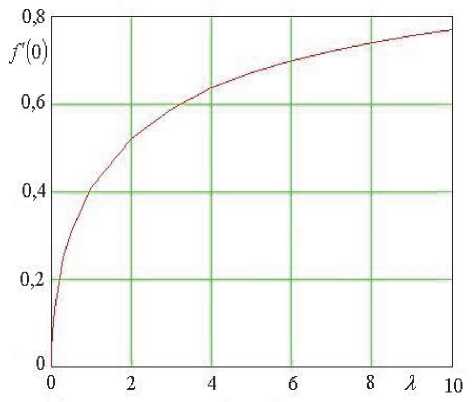
Рис. 2. Зависимость безразмерной скорости газа на границе раздела сред от параметра X

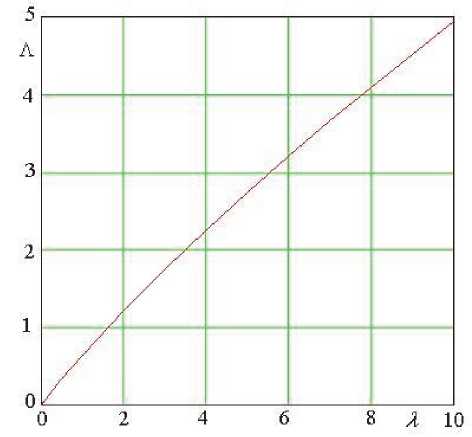
Рис. 4. Связь между параметрами X и Л

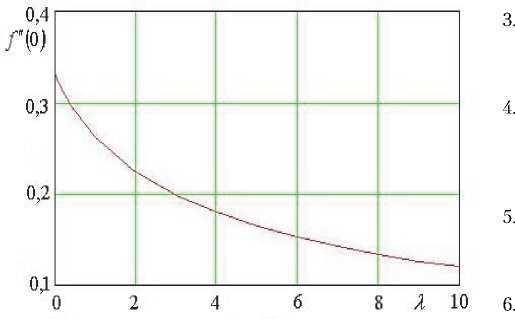
Рис. 3. Безразмерное трение на поверхности пластины в зависимости от параметра X