Двухстороннее связывание при моделировании взаимодействия сверхзвукового потока и деформируемой пластины. Cравнение численных схем и результатов эксперимента

Задачи численного моделирования взаимодействия деформируемого твердого тела и газа/жидкости (FSI — Fluid-Structure Interaction) в последнее десятилетие привлекают к себе все большее внимание, что обусловлено как развитием методов, алгоритмов, вычислительных систем, так и растущей востребованностью результатов при решении широкого круга прикладных проблем. В качестве типичных примеров можно привести задачи внутренней баллистики ракетных двигателей на смесевом твердом топливе [1], исследования аэрогидроупругости аэродинамических элементов летательных аппаратов [2], предотвращения флаттера лопаток турбореактивных двигателей, гидродинамики судов на воздушной подушке с эластичными юбками, определения деформаций конструктивных элементов турбин и компрессоров и многие другие.

Подобного рода задачи являются сопряженными, прежде всего в том смысле, что требуют совместного решения как уравнений динамики деформирования твердого тела, так и уравнений газодинамики. Существуют два основных подхода для связывания: монолитный и последовательный. Монолитный подход подразумевает применение таких численных схем, результатом которых является формирование и последующее решение единой системы алгебраических уравнений. При последовательном подходе, основанном на раздельном решении систем уравнений для каждой подзадачи, требуется реализация обменов данными вычислений между подзадачами через заданный интервал времени [3].

Последовательный (раздельный) метод решения газодинамических и прочностных задач позволяет очевидным образом учитывать их специфику. Однако, как все явные методы разделения, он проявляет неустойчивость, так как на каждом временном шаге численные решения физических подзадач, строго говоря, не согласованы между собой. Для большинства типов схем разделения обеспечивается согласование положения границ расчетных областей, но при этом нагрузки на эти границы получаются разными со стороны конструкции и стороны газа [3]. Тем не менее, для определенного класса задач необходимая точность решения может быть достигнута.

Исследование вопросов адекватности различных методов и алгоритмов, применительно к рассматриваемому классу сопряженных задач, осложнено отсутствием точных аналитических решений и недостаточным количеством экспериментальных исследований, что значительно затрудняет верификацию применяемых алгоритмов и программ.

В настоящей работе рассматривается математическая модель нестационарного течения в канале сложной формы, имеющем преграду в виде защемлённой деформируемой упругой панели. Тестируются

различные подходы двухстороннего связывания для учёта взаимодействия потока газа и деформируемой панели, использующие различные методы дискретизации уравнений по пространству и, как следствие, несогласованные расчетные сетки. В газодинамике — это метод конечных объёмов, в механике деформируемого твердого тела — метод конечных элементов. Результаты численного моделирования сравниваются с данными одной из немногих известных экспериментальных работ в данной области [4].

1.    Постановка задачи

В работе формулируется математическая модель взаимодействия сверхзвукового потока газа и деформируемой пластины в ударной трубе с учетом максимального соответствия условиям проведения эксперимента [4]. Рассматриваемые экспериментальные результаты получены на установке «Т80» [5], которая представляет собой ударную трубу длиной 3,75 м (Рис. 1). Рабочий поток создаётся в результате нестационарного расширения воздуха, сжатого в камере высокого давления до величины 0,254 МПа. Разрыв мембраны при запуске установки обеспечивает формирование распространяющейся со скоростью 1,21 M ударной волны, которая в дальнейшем взаимодействует с защемлённой по краю деформируемой пластиной. Малая продолжительность испытания позволяет пренебречь влиянием турбулентности и процессов теплообмена между газом, корпусом установки и деформируемой панелью. В рассматриваемом диапазоне температур и давлений рабочее тело (воздух) можно считать совершенным газом с показателем адиабаты у = 1,41.

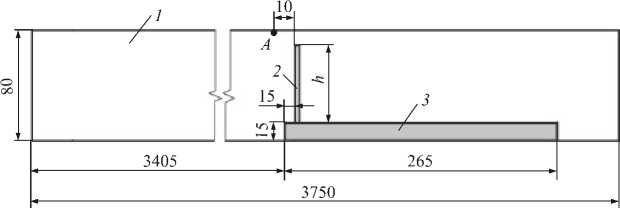
Рис. 1. Схема экспериментальной установки: 1 - труба; 2 - пластина толщиной l = 1 мм; 3 - недеформируемое основание

Деформируемая пластина, изготовленная из стали плотностью р = 7600 кг/м³ и модулем Юнга E = 220 ГПа, полагается изотропным и однородным упругим телом. Малые величины деформаций и скоростей деформаций делают влияние демпфирования пренебрежимо малым, что дает возможность решать задачу деформирования в рамках физически и геометрически линейной трехмерной теории упругости.

К сожалению, недостаточные точность и подробность имеющихся экспериментальных данных не позволяют дать обоснованную оценку необходимости учета в математической модели турбулентности потока, теплопередачи в стенки, трехмерных эффектов (неизбежно имеющих место при проведении любого физического эксперимента) и даже влияния вязкости. Поэтому все эти вопросы оставлены за рамками данной статьи.

В задачах взаимодействия газа с деформируемым телом необходимо сформулировать дополнительные кинематические и динамические граничные условия на контактных поверхностях. Пусть имеется физическая область Q , ограниченная поверхностью 50 . Область разделена на части, занимаемые газом Q g ( t ) и деформируемым твердым телом (пластиной) Q s ( t ) так, что Q ( t ) = Q s ( t ) U Q g ( t ). Граница раздела Г ( t ) между Q s ( t ) и Q g ( t ) существует и в каждый момент времени определяется как Г ( t ) = Q s ( t ) П Q g ( t ). Далее будем применять обозначения Г g и Г s , если речь пойдет только о подобластях, занятых газом и деформируемым телом соответственно.

Так как пластина предполагается непроницаемой для газа, то для произвольного момента времени на Г ( t ) скорости и ускорения тела должны быть равны скоростям и ускорениям газа:

I

u , ( t ) = U g ( t ),       u , ( t ) = U g ( t ).

Эти равенства выражают условия кинематической совместности. Условия динамической совместности имеют вид

Ps n s = Pg n g , где ps, pg — давление; ng,ns — внешние нормали (ng =-ns).

Из (1) и (2) следует, что на границе Г, движущейся со скоростью UГ, справедливы законы сохранения массы, импульса и энергии. При этом для удовлетворения закона сохранения энергии на границе необходимо выполнение равенства t+A t

J J U r g ■ P g n g dtd ^Г g = J ( u s ( t ^{+ A} t ) - u s ⁽ t ) ) • P s n s d ^Г s .                             ⁽³⁾

^Г g t                                  ^Г s

Отметим, что наличие в (3) интеграла по времени говорит о том, что при численной реализации может сыграть существенную роль не только способ интегрирования, но и момент времени, при котором происходит обмен информацией между подобластями Q _s и Q _g . Рассматриваемое течение газа, с учетом сделанных допущений, может быть описано следующей системой уравнений сохранения:

|p+v(pgиg)=0, Hp.' 1+V(pgиgиg)=-vPg-^g, ^^ + V^ gEg U g ) = — Pg (V U g ^V q — ^ g ' VU g ) ,

где p _g — плотность газа, p_g — давление, U _g — вектор скорости, ст _g =-p ( v U _g + ( V U _g ) ) + 2 ц ( V U _g ) I /3 — тензор вязких напряжений, E_g = U g /2 + c v T — полная энергия, T — температура, q — тепловой поток. Система (4) замыкается уравнением состояния идеального газа p_g = p _gRT .

Расчетная область Q _g представляет собой внутреннее пространство ударной трубы с закрепленной в измерительной секции деформируемой пластиной (Рис. 1). Граничные условия определяются обычным образом для непроницаемой твердой теплоизолированной стенки: U _g = 0 на Г \ Г _g d q /5 п = 0 на Г . ^,

На границе Г скорость газа совпадает со скоростью движения границы U = Ur . Начальные данные g                                                                                                                  g        1 g соответствуют условиям проведения эксперимента [4]: T = 293 K, Ug = 0 , давление в камере (x < 0,75 м) p1 = 0,254 МПа и канале p2 = 0,1 МПа.

Динамику напряженно-деформированного состояния пластины опишем системой уравнений divGs +p sb =psus , где стs = Xtrs(us)I + 2ps(us) — тензор напряжений Коши; e(us) = (1/2)(Vus +VuT) — тензор малых деформаций; ps — плотность тела.

Выбор между слабосвязанной и жесткосвязанной постановками сопряжения зависит от класса решаемой задачи и обуславливается интенсивностью взаимодействия (прежде всего количеством обменов импульсом за время шага интегрирования по времени) между деформируемым телом и потоком газа. Анализ экспериментальных данных [4] позволяет предположить, что для численного решения рассматриваемой задачи с использованием схемы интегрирования, реализующей слабое связывание, удовлетворительные результаты могут быть получены при одном обмене данными (вычисленным полем давления в газе и перемещениями в конструкции) на каждом шаге по времени. Отметим, что в данной работе рассмотрены особенности взаимодействия газа с пластинами различной высоты h = 50 мм и h = 40 мм. Кроме того, сопоставление приведенных в работе [4] численных результатов с экспериментальными выявляет порой существенное их различие. Поэтому представляется интересным сравнительный анализ применения алгоритмов слабого и жесткого двухстороннего связывания, обеспечивающих достижение заданной точности решения на общей границе Г ( t ) — интерфейсе.

Для наглядности представления схем связывания отдельных задач введем обозначения: p _Г , и _Г — давление и перемещение границы сопряжения. Тогда на временном шаге t n ⁺¹ перемещения u Г⁺¹ , полученные из решения задачи деформирования с заданной на границе нагрузкой, обусловленной давлением газа p Г ⁺¹ , можно выразить через функцию S : и Г⁺¹ = S ( p Г⁺¹ ) . Аналогично, решение газодинамической задачи для давления на интерфейсной границе обозначим как p Г⁺¹ = F ( и Г⁺¹ ) . Теперь, используя введенные обозначения, задачу сопряжения можно представить в виде системы нелинейных уравнений

u ;⁺¹ = S [ F ( u ;⁺¹ ) ] = S о F ( u ;⁺¹ ) .

При применении неявных схем интегрирования, используемых в каждом приложении, соответствующие отдельным задачам системы уравнений примут вид

u:+1 = s (un+1, u n, p;+1), n+1 =F / n+1   n   n+1\ pg          pg,pg,s .

Тогда в случае слабосвязанной постановки задачи система уравнений будет иметь следующий вид:

u n ⁺¹ = s ( u n ⁺¹ , u n , p g ⁺¹ ) , p g ⁺ F ( p g ⁺ . p g , u n ) ■

Для решения системы уравнений (5) требуется единственный обмен данными на каждом временном шаге. В жесткосвязанной постановке соответствующая система un+1, k+1 = S (unn+1, k+1, unn, pn+1, k+1

_ n+1, k+1             n+1, k+1    n n+1, k pg     = F ( pg , pg , us

решается итерационным методом. Последовательное решение каждой задачи на временном шаге t^{n +1} (внешний итерационный цикл) использует решение на предыдущем временном шаге, и затем выполняется несколько приближений, обозначенных индексом k (внутренний итерационный цикл для каждой физической подзадачи) по схеме (6) до достижения сходимости по скоростям ||U g⁺¹’^{k + 1} - U g⁺¹’^k ||, перемещениям ||u n ^{+1, k +1} - u n ^{+1, k} || или давлению || p g ^{+1, k +1} - p"_g ^{+1, k} ||. Как правило, в этом случае используются классические итерационные методы типа Гаусса–Зейделя или ньютоновского типа.

2.    Математические модели и алгоритмы расчета

В работе рассматривалось два подхода к решению поставленных задач. Первый реализован при помощи авторской системы связывания, объединяющей программное обеспечение (ПО) OpenFOAM [6] и FEStudio [7], и использует механизмы синхронизации и передачи данных ICE [8]. Второй подход заключается в применении средств коммерческого программного комплекса ANSYS 12.1 для решения сопряженных задач на кластере «Уран» ИММ УрО РАН (г. Екатеринбург). В рамках первого подхода задачи газовой динамики и механики деформируемого твердого тела решались последовательно, соответственно, с помощью ПО OpenFOAM и FEStudio. При этом двухсторонний обмен данными на границе сопряжения, допускающий использование только алгоритмов слабого связывания, реализован и в разработанном авторами промежуточном ПО, и в его текущей реализации. В связи с этим, значительный интерес представляет тестирование функциональных возможностей комплекса ANSYS 12.1 и встроенного ПО Multi-Field Solver, которое обеспечивает решение сопряженных задач как в слабосвязанной, так и в жесткосвязанной постановках.

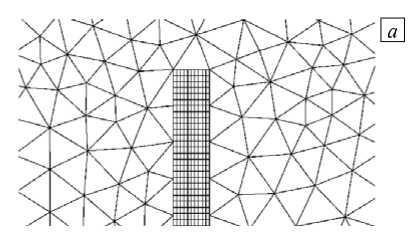
Во всех рассматриваемых случаях задачи решались на несогласованных сетках, примеры которых приведены на рисунке 2.

а

Рис. 2. Увеличенные фрагменты несогласованных расчётных сеток вблизи верхнего края пластины, используемые при расчетах: ПО OpenFOAM [6] и FEStudio ( а ); ANSYS Multi-Field Solver 12.1 ( б )

б

Отметим некоторые особенности применения ANSYS Multi-Field Solver 12.1. Двухстороннее связывание ANSYS CFX 12.1 и ANSYS Structural 12.1 обеспечивается модулем MFX, предоставляющим довольно скудный выбор параметров и алгоритмов связывания, интерполяции и деформирования сеток [9]. Особо следует выделить его значительные требования к объему оперативной и дисковой памяти для применяемых расчётных сеток. Решение сопряженной задачи потребовало существенных временных затрат. Расчет на одном временном шаге ( A t = 10 -6 с) при слабосвязном алгоритме занимал 6 с физического времени для 64 узлов (против 5 с на OpenFOAM+FEStudio), а при жесткосвязанном алгоритме (при к = 20 ) — 60 секунд для 8 узлов, 54 с для 16 узлов и 21 с для 64 узлов. Как видно, параллельная масштабируемость и эффективность вычислений невысоки. В реализации первого подхода OpenFOAM+FEStudio потенциально заложено несколько уровней распараллеливания и больше возможностей выбора алгоритмов при решении связанной задачи. Апробированные алгоритмы и схемы представлены в таблице.

Таблица. Характеристики использованных моделей, алгоритмов и программ

Оригинальные методы и алгоритмы [4]	Рассмотренные в данной работе алгоритмы OpenFOAM+FEStudio	Коммерческий программный пакет ANSYS Multi-Field Solver 12.1
1. Расчетная сетка
Расчетная сетка в области, занятой газом, содержала 80 000 ячеек в 8 доменах, сгущалась до характерного размера 0,01 мм	Расчётная сетка (Рис. 2, а ) содержала 380 000 ячеек, сгущалась до характерного размера 0,1 мм. Применялись элементы в виде треугольных призм, совпадающие с ячейкой сетки [6], обеспечивающие устойчивость алгоритма деформирования сетки [7]	Расчётная сетка (Рис. 2, б ) содержала 140 000 элементов, 530 000 узлов, имела дополнительное разрешение до характерного размера 1 мм. Применялись элементы в виде шестигранника
2. Газодинамика
Система уравнений газовой динамики численно решалась конечно-объемным методом с применением ограничителя Ван Лира [10]		Система уравнений газовой динамики решалась конечно-объемным методом, встроенным в пакет ANSYS CFX 12.1 [11]
3. МДТТ
Использовались линейная конечно-элементная аппроксимация перемещений и схема Ньюмарка по времени		Использовался      пакет      ANSYS Structural[11]
4. Постановка задачи FSI
Cлабосвязанная	Cлабосвязанная	Слабосвязанная и жесткосвязанная
а) Интерполяция сеточных данных
Применялся метод интерполяции данных [12]	Применялся метод интерполяции данных, основанный на построении матриц преобразований [13]	Применялся консервативный тип интерполяции, производящий полный перенос параметров, полученных с использованием одной сетки, на другую сетку [11]
б) Алгоритм деформации сетки
Реализовался     оригинальный алгоритм [4]	Модификация сетки осуществлялась методом, сохраняющим топологию исходной сетки и основанным на представлении связности узлов через «пружинную» аналогию [14]. Новые координаты узлов сетки определялись из решения методом конечных элементов в ПО FEStudio краевой задачи упругого деформирования	Модель движения и деформации сетки основывалась на представлении связности узлов через «пружинную» аналогию [11]

3.    Результаты численного моделирования

По аналогии с [4] исследованы два варианта взаимодействия нестационарной ударной волны с деформируемой пластиной, различающиеся только высотой пластины ( h = 50 мм и h = 40 мм), что дало возможность выполнить непосредственное качественное и количественное сравнение полученных результатов с данными, представленными в [4].

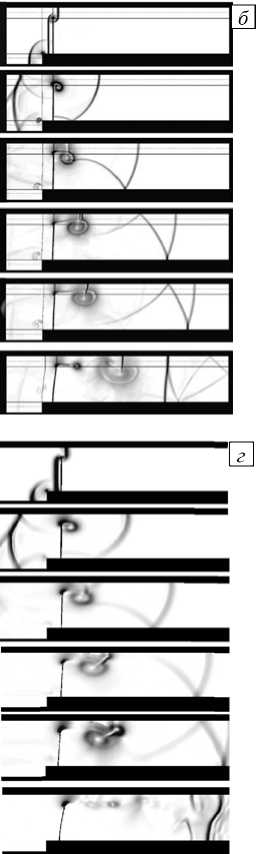
Общая картина течения (Рис. 3) в основном определяется динамикой падающей ударной волны и порождаемым ею семейством отраженных волн. На рассматриваемом отрезке времени различия течения между экспериментальными вариантами h = 50 мм и h = 40 мм незначительны, поэтому приведены результаты только для h = 50 мм. За начальный выбран момент времени, когда в результате взаимодействия пластины и падающей прямой ударной волны образуется отраженный плоский скачок уплотнения, движущийся против потока. При этом скорость набегающего потока вблизи пластины существенно понижается. Одновременно начинается образование цилиндрической ударной волны на верхней кромке пластины, фронт которой к моменту времени t = 140 мс достигает нижней стенки.

Обтекание потоком газа верхней кромки пластины приводит к зарождению устойчивого вихря, который затем, смещаясь вниз по потоку, увеличивается в размерах (к моменту t = 280 мс). Сформировавшаяся в результате переотражений цилиндрической волны от нижней и верхней стенок канала система скачков уплотнения ( t = 420 мс), теряя интенсивность, образует так называемую X -конфигурацию ( t = 490 мс), сохраняющуюся вплоть до достижения правой границы канала. До этого момента времени численное решение, полученное как в разрабатываемом комплексе OpenFOAM+FEStudio, так и в ANSYS (Рис. 3, в , г ) хорошо согласуются и с результатами расчета (Рис. 3, б ), и с экспериментальными данными (Рис. 3, а ) из [4].

Заметное различие результатов моделирования обнаруживается далее, когда отраженная от правой границы канала волна, движущаяся против потока, взаимодействует с вихревыми структурами ( t = 910 мс), при этом отклонение верхней кромки пластины ( u s ( t ) = - max [ u _s (0) - u _s ( t ) ] i , где i = (1,0,0)), близко к максимальному (Рис. 3, б ). На теневой фотографии (Рис. 3, а ) и в картинах, установленных расчетами по авторской модели связывания задач (Рис. 3, в ) и жесткосвязному алгоритму с применением ANSYS (Рис. 3, г ), отсутствуют вихри (Рис. 3, б ), выявленные в результате численного моделирования в [4]. Вероятнее всего появление вихрей в [4] объясняется физически некорректной постановкой краевых условий на левой границе расчетной области, вследствие чего получаются завышенные значения скорости набегающего потока.

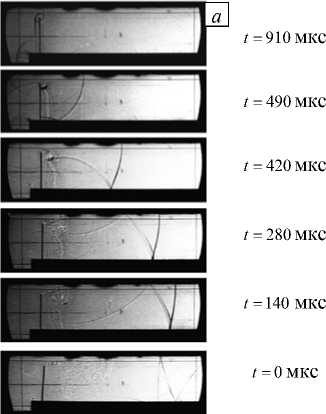
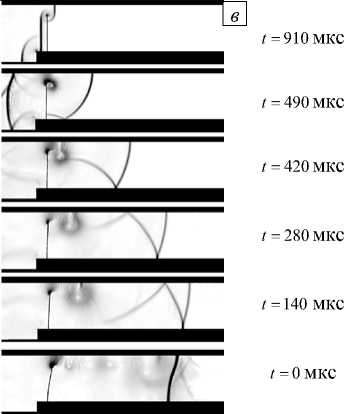
Рис. 3. Картина течения в различные моменты времени при высоте пластины h = 50 мм: эксперимент [4] ( а ); расчет [4] ( б ); расчет по авторской модели ( в ); расчет в ANSYS при жесткосвязной постановке ( г )

На рисунке 4 представлены результаты изменения во времени отклонения верхней кромки пластины ( h = 40 мм) и значений давления в точке «А» (Рис. 1). Смещению кромки против потока соответствуют положительные значения на графиках. Прежде всего следует отметить хорошее соответствие отклонения пластины, рассчитанного с использованием рассмотренных алгоритмов и программных сред (Рис. 4, а , кривые 3 , 4 ) с экспериментальными данными (кривая 1 ), так как именно определение деформации конструкции под воздействием потока газа и представляет основной практический интерес в подобного

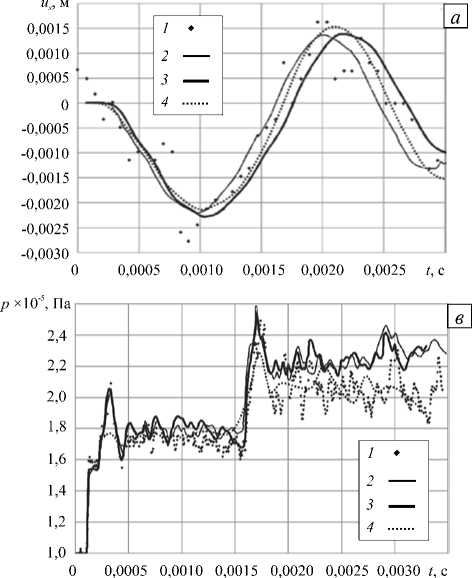
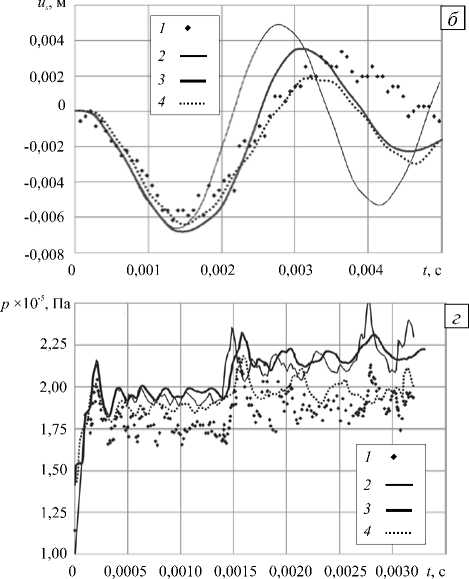
Рис. 4. Зависимости перемещения края пластины ( а , б ) и давления ( в , г ) от времени при h = 40 мм ( а , в ) и h = 50 мм ( б , г ): кривая 1 – эксперимент [4]; 2 – расчет [4]; 3 – расчет по авторской модели; 4 – расчет в ANSYS при жесткосвязной постановке

рода задачах. Рассчитанные колебания давления (Рис. 4, б , кривые 3 , 4 ) также удовлетворительно согласуются с физической картиной течения, что следует из совпадения положений максимумов, соответствующих прохождению отраженной от пластины ударной волны ( t = 0, 0002 с) и затем волны, отраженной от правой стенки канала ( t = 0, 0017 с).

Анализ результатов моделирования колебаний более податливой пластины высотой h = 50 мм свидетельствует, что рассчитанная зависимость отклонения верхней кромки (Рис. 4, в , кривые 3 , 4 ) существенно ближе к экспериментальным данным (кривая 1 ), чем результаты вычислений [4] (кривая 2 ). По-видимому, это объясняется тем, что в данной работе расчетная область в точности совпадает с внутренним пространством экспериментальной установки, что дает возможность на всех границах использовать условия для непроницаемой теплоизолированной стенки и избежать введения в модель каких-либо дополнительных искусственных границ. По этой же причине достигается более точное совпадение во времени положений максимумов рассчитанного давления (Рис. 4, г , кривые 3 , 4 ) с экспериментальными данными (кривая 1 ).

Однако влияние схемной вязкости сказывается на размывании и вытягивании кривой при использовании жесткосвязанной постановки при реализации в ANSYS, (Рис. 4, г , кривая 4 ). Отдельно для сравнения приведены результаты, полученные в ANSYS в слабосвязанной и жесткосвязанной постановках (Рис. 5). Применение слабосвязного алгоритма+ANSYS приводит

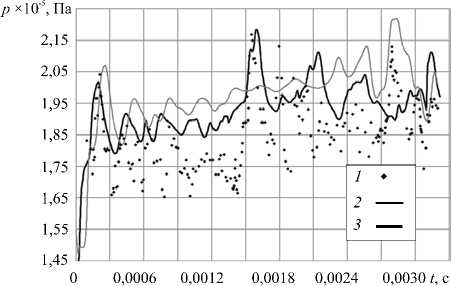
Рис. 5. Графики зависимостей давления от времени h = 50 мм: 1 — эксперимент [4]; 2 — расчет в ANSYS при жесткосвязанной постановке; 3 — расчет в ANSYS при слабосвязанной постановке

к сглаживанию второго пика давления, уменьшению амплитуды колебаний до 15%, снижению частоты колебаний на 23%. Отметим, что при моделировании с помощью ПО OpenFOAM+FEStudio подобное поведение численного решения не наблюдается. Это может быть обусловлено особенностями алгоритма ANSYS CFX 12.1, использующего искусственную вязкость для обеспечения вычислительной устойчивости. В случае жесткосвязанной постановки+ANSYS максимальное число итераций связывания на временном шаге задавалось k = 20 . Полученная кривая давления (Рис. 4, г, кривая 4) близка к результатам для слабосвязанного алгоритма+OpenFOAM+FEStudio до момента времени t = 0, 015 (Рис. 4, г, кривая 2), а для последующих значений времени наблюдается ее хорошее соответствие экспериментальным данным [4] (Рис. 4, г, кривая 1). Диссипативные свойства численной схемы ANSYS CFX 12.1, по-видимому, точнее соответствуют процессам перехода кинетической энергии потока в тепловую, происходящим при взаимодействии отраженных от правой стенки канала ударных волн как с пластиной, так и с вихревыми структурами.

4.    Заключение

Рассмотренная задача исследования колебаний упруго-деформируемой пластины под действием набегающего сверхзвукового потока газа является одной из немногих, имеющих подробное экспериментальное описание, что дает возможность выполнять проверку и сравнительное тестирование разрабатываемых моделей, алгоритмов двухстороннего связывания и создаваемых новых программ, предназначенных для численного изучения широкого круга явлений нестационарного взаимодействия в системе «газ – конструкция».

Выполненное сравнение результатов численного моделирования с экспериментальными данными позволяет заключить, что предложенные модели и алгоритмы связывания адекватно описывают происходящие физические процессы как в газе и деформируемой пластине, так и их взаимное влияние в рамках слабосвязной постановки задачи OpenFOAM+FEStudio и жесткосвязной постановки ANSYS. Некоторые алгоритмы, как например интерполяция данных между узлами несогласованных сеток, деформация сеток, требуют дополнительного совершенствования и тестирования при рассмотрении трехмерных задач в разрабатываемом программном комплексе. Кроме того, актуальным является снижение вычислительных затрат на решение сопряженной задачи и распараллеливание всех шагов алгоритма жесткого связывания.

Работа выполнена в рамках программы Президиума РАН № 18 при финансовой поддержке УрО РАН (проект 12-П-1-1005) и РФФИ (проекты № 11-01-00275-a, 12-07-00080-а).