Двухуровневая модель для описания поведения сталей при термомеханическом нагружении с учетом мартенситных превращений: алгоритм реализации модели
Автор: Исупова Ирина Леонидовна, Трусов Петр Валентинович
Журнал: Вычислительная механика сплошных сред @journal-icmm
Статья в выпуске: 4 т.6, 2013 года.
Бесплатный доступ
Приведено краткое описание модели для анализа поведения сталей при термомеханическом нагружении с учетом мартенситных превращений. При построении модели применяется многоуровневый подход, основанный на введении в ее структуру внутренних переменных – параметров, характеризующих состояние и эволюцию мезо- и микроструктуры материала. Решение связанной задачи сводится к решению трех подзадач – теплопроводности, определения напряженно-деформированного состояния и нахождения объемных долей сосуществующих фаз, что значительно облегчает процесс получения решения. Для решения указанных подзадач, в свою очередь, предлагаются различные типы моделей. В статье представлен подробный алгоритм реализации модели, включающей все три подзадачи, на двух рассматриваемых масштабных уровнях. С использованием разработанного алгоритма выполнены численные эксперименты и проанализированы результаты расчетов в случаях простого и сложного нагружения представительного объема макроуровня. При проведении численных экспериментов учитывается изменение температуры за счет пластической деформации и теплоты фазовых превращений.
Стали, мартенситные превращения, двухуровневая модель
Короткий адрес: https://sciup.org/14320701
IDR: 14320701 | УДК: 539.3 | DOI: 10.7242/1999-6691/2013.6.4.54
Текст научной статьи Двухуровневая модель для описания поведения сталей при термомеханическом нагружении с учетом мартенситных превращений: алгоритм реализации модели
Между структурой и физико-механическими свойствами сталей существуют тесные связи. Различные режимы термомеханического воздействия позволяют в широких пределах изменять микроструктуру, а следовательно, механические, физико-химические и эксплуатационные свойства сталей. Очень часто термомеханические воздействия могут стать причиной появления различных типов фазовых превращений. Возможность протекания тех или иных фазовых превращений и их кинетика зависят от таких параметров воздействия, как температура, условия нагрева, длительность выдержки, скорость охлаждения, характеристики механического нагружения. Корректное описание изменения структуры материалов, в том числе и за счет протекающих фазовых превращений, дает возможность разработки новых методов создания материалов с заданным набором свойств и оптимизации уже существующих материалов и технологий.
Экспериментальное исследование данного вопроса является достаточно ресурсоемким, особенно в случае сложного механического нагружения, поэтому в механике деформируемого твердого тела актуальной становится задача построения моделей, описывающих состояние и эволюцию структуры материала с учетом твердотельных фазовых превращений. В последнее время в литературе появилось значительное количество работ, где для моделирования как диффузионных [1, 2], так и бездиффузионных (мартенситных) [3–5] превращений применяется метод фазового поля, который предполагает наличие «размытой» границы между фазами. Форма и взаимное расположение областей, занимаемых отдельными фазами, устанавливается совокупностью параметров, определяющих доли фаз, изменение которых во времени подчиняется кинетическому уравнению, полученному в рамках термодинамики необратимых процессов. При таком подходе для решения задачи чаще всего используется метод конечных элементов; в качестве моделируемой области выступает объем, состоящий из нескольких зерен. Подобным образом с помощью метода фазового поля можно детально воспроизвести внутреннюю структуру материала,
но для моделирования процессов термомеханической обработки этот подход малопригоден из-за огромных вычислительных затрат.
Часто для определения поведения сталей с учетом фазовых превращений прибегают к прямым моделям, основанным на физической теории пластичности и учитывающим происходящие фазовые превращения [6–9]. При этом конститутивная модель строится исходя из термодинамического подхода. Данные модели также применяются для представления поведения областей, являющихся отдельными зернами или их совокупностями, поскольку математическое описание реальных процессов с последующим применением метода конечных элементов в трехмерной постановке требует существенных вычислительных затрат.
Процессы фазовых превращений при термомеханической обработке сталей на уровне целых конструкций описываются, как правило, с помощью кинетических макромоделей [10, 11]. Далее для решения поставленной задачи также используется метод конечных элементов. Объемные доли сосуществующих фаз находятся из феноменологических соотношений, полученных при большом числе допущений. При рассмотрении неупругого поведения применяются достаточно простые модели, в которых отсутствует прямое включение механизмов деформирования и фазовых превращений, а также вызывающих их воздействий, присущих в реальном материале различным структурным уровням.
Из приведенного краткого обзора можно сделать вывод, что проблему построения наиболее полной модели неупругого деформирования сталей с учетом мартенситных превращений при разнообразных условиях термического и механического воздействия нельзя назвать полностью решенной. В данной работе авторами предлагается многоуровневая модель поведения сталей при термомеханической нагрузке с учетом фазовых превращений в мартенситном диапазоне. Преимуществом модели является введение в ее структуру параметров (внутренних переменных), описывающих состояние и изменение микроструктуры материала [12, 13]. Рассматриваются структура модели, ее масштабные уровни и алгоритм реализации на всех уровнях. Возможности модели продемонстрированы на примере решения задачи исследования деформирования представительного объема материала на макроуровне в условиях простого и сложного нагружения. Проведены анализ результатов моделирования и сопоставление с доступными данными натурных экспериментов.
-
2. Двухуровневая модель поведения сталей при термомеханическом нагружении, учитывающая мартенситные превращения
При построении модели поведения сталей в работе применяется многоуровневый подход. В этом случае процессы деформирования и фазовых превращений в материале исследуются не только на макроуровне, но и на более глубоких масштабах, на которых учитываются присущие им механизмы деформирования и фазовых превращений. Связь уровней осуществляется за счет введения в определяющие соотношения каждого масштабного уровня явных внутренних переменных, которые находятся из замыкающих уравнений, отображающих процессы деформирования и фазовых превращений на более глубоких (по отношению к рассматриваемому) масштабах. В соответствии с особенностями процессов деформирования и микроструктуры вводятся следующие масштабные уровни: уровень физического тела (макроуровень I), уровень представительного макрообъема (макроуровень II) и мезоуровень. При этом непосредственно к модели материала относятся только макроуровень II и мезоуровень. Элементом мезоуровня является зерно, а представительный объем макроуровня состоит из множества элементов мезоуровня.
Для облегчения моделирования процессов, происходящих в сталях при термомеханическом нагружении, связанная задача «расщепляется» по физическим процессам. Этот прием позволяет при постановке и последующем решении выделить относительно независимые подзадачи, а именно подзадачи нахождения НДС, температуры и фазовых долей всех сосуществующих фаз.
На макроуровне I ставится и решается краевая задача, включающая в свою постановку уравнение равновесия в скоростях, определяющие и кинематические соотношения, уравнение теплопроводности, необходимые граничные и начальные условия [14, 15]. В задаче НДС элемент макроуровня II представляется выборкой соответствующих элементов мезоуровня [16, 17]. Параметры нагружения с макроуровня II на мезоуровень передаются с помощью гипотезы Фойгта. Неупругая составляющая градиента относительной скорости перемещений, тензор спина и физико-механические свойства на макроуровне II устанавливаются из условия согласования определяющих соотношений двух масштабных уровней. При этом на мезоуровне используются несимметричные меры напряженного и деформированного состояний, а при переходе на макроуровень осуществляется симметризация меры напряжений [18].
На мезоуровне принимается приведенная ниже совокупность основных положений и соотношений. В качестве меры скорости изменения деформированного состояния берется транспонированный градиент относительной скорости перемещений Z r : Z r = v V - to , где v — скорость перемещений; го — тензор спина; индекс « r » указывает на величины, характеризующие относительное движение, фиксируемое наблюдателем в жесткой подвижной системе отсчета мезоуровня. Неупругое деформирование элемента мезоуровня может осуществляться за счет мартенситных превращений и пластических деформаций.
Изменение объемной доли i -го варианта мартенсита ^t описывается следующим кинетическим соотношением [15]:
5^ -- m l [ 1 5 f - 1 5 f ' d t Z j ^3^ 05 j
где I j — кинетические коэффициенты, 0 — температура, f — свободная энергия Гиббса.
Скорость сдвига по системе скольжения у ( к ) записывается в виде вязкопластического закона:
Y ( k )
( к )И(А к ) _( к )\
-У 0 H ( Т i -т ci )
т ( к )
ci
1/ mci
т ( к ) - b ( к ) n ( k ) : о ,
где у 0 k ) — материальный параметр; mci — параметр скоростной чувствительности; H ( ■) — функция Хэвисайда; т ( к ) и т ( к ) — сдвиговое и критическое напряжения, действующие в к -й системе скольжения; о — тензор напряжений Коши; b ( к ) — единичный вектор по направлению вектора Бюргерса, n ( к ) — единичный вектор нормали к плоскости скольжения. Стоит отметить, что принимается удвоенное число систем скольжения, то есть системы скольжения с положительным и отрицательным направлениями сдвига считаются различными. Индекс « i » указывает на принадлежность величины конкретной фазе (аустениту или одному из вариантов мартенсита).
Скорости изменения критических напряжений сдвига для k -й системы скольжения являются функциями параметров процесса и материала [19, 20] и вычисляются по формуле:
\ V ,
т( к ) = т1 т ci т
n
: С 0 Z a к k
V
_i
n
Zy“
V i -1 7
Y ( i )
- B,0
p k ) p ci
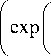
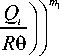
m 2 i
- 1
n
Z 7+g ( k 1 ,
где p — начальный предел текучести в к -й системе скольжения; v,, B, m1i, m2i, т ci — материальные константы; Q, — энергия активации; a('ki) — модули упрочнения; y(j) — накопленный сдвиг по i -й m2
системе скольжения. Последнее слагаемое для аустенита имеет следующий вид: g(k) - z; H*кi, где H*кк i-1
характеризует скорость упрочнения аустенита из-за увеличения объемной доли образующегося i -го варианта мартенсита. Для мартенсита функция g(к) выглядит как g(к) - ^, < т^к) - Тк0 >, где < х >- х Н (х). Таким образом, в многофазной системе скорость неупругих деформаций за счет двух описанных выше механизмов находится из соотношения
n zг -Z1 ^i Z b(к)n(к)Y(кк
( к -1
m
-Z^ i f i ,
f i * — градиент трансформационной деформации; m 1 — число фаз, испытывающих пластическую деформацию; m 2 — количество разновидностей мартенсита, которые могут образоваться в процессе фазового превращения.
Спин ω вычисляется в соответствии с моделью полностью стесненного поворота Тейлора:
№ - 2 ( v v - v v ) - 2 ^Z Y A ) ( ь Ак ) п Ак )- п Ак ) ь Ак ) ) .
Для меры скорости деформаций принимается гипотеза о возможности ее разложения на упругую, неупругую (пластическую и трансформационную) и термическую составляющие. В качестве определяющего соотношения используется закон Гука в скоростной релаксационной форме:
a cr = a - to ■ a + a ■ го = и : ( Z r - Z in - « 9 ) ,
где индекс « cr » означает коротационную производную. Следует отметить, что в многофазной системе тензор упругих свойств п и тензор термического расширения α подчиняются правилу смеси.
Определяющее соотношение на макроуровне II (в скоростной форме) также записывается в виде обобщенного закона Гука:
E cr = E + E ■ Q + Q1 ■ E = П: (Zr - Z‘rn - A0), где E, Ecr — тензор напряжений Коши и его коротационная производная; Zr = VV -Q — транспонированный градиент относительной скорости перемещений (V — скорость перемещений); неупругая составляющая градиента относительной скорости перемещений Zrin , тензор спина Ω , тензор упругих свойств П и тензор термического расширения А находятся из условий согласования определяющих соотношений макроуровня II и мезоуровня:
Z in ! у in \ । / / А/ \ । ТТ-1 . /с . / . f in / । । ,„/А/ \\ ТТ-1 . / С . (/ \ / \\\
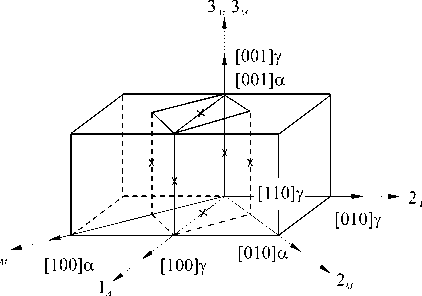
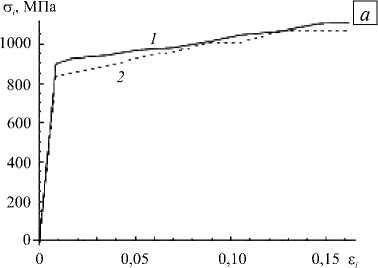
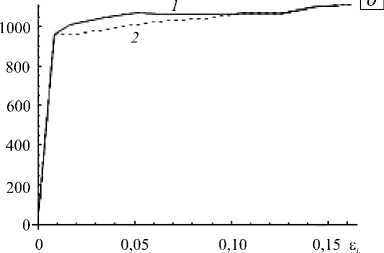
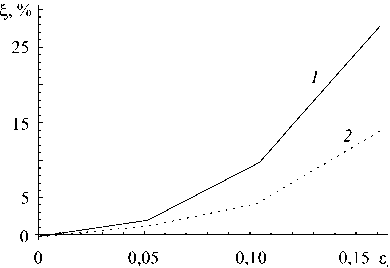
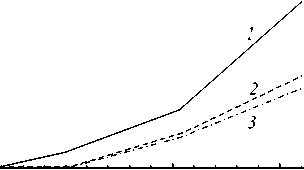
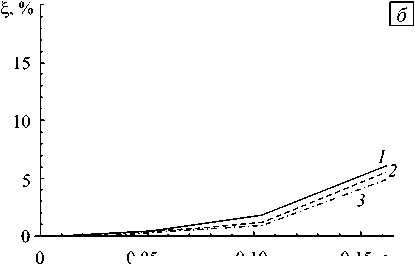
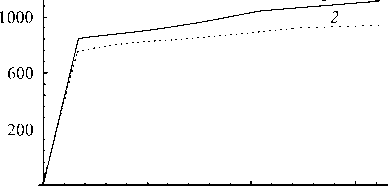
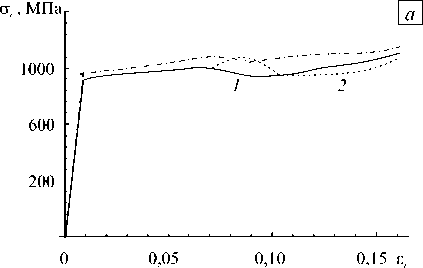
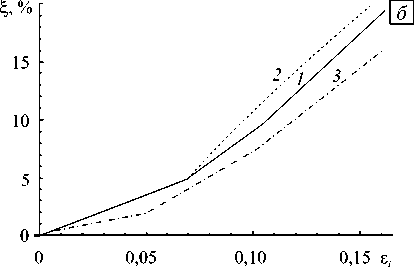
r = Q = (to), П = (S: и), A = (a). Здесь S = (CII + Сш)/2 — тензор четвертого ранга (CII, Сш — изотропные тензоры четвертого ранга), который на произвольный тензор второго ранга T действует следующим образом: S: T = (T + TT)/2 = Ts; штрихом обозначаются отклонения величин от их средних значений. В температурной задаче каждой макроскопической точке интегрирования (элементу макроуровня II) приписывается совокупность зерен с заданным распределением ориентаций, а каждый элемент мезоуровня аппроксимируется совокупностью конечных элементов [16, 17]. Тензор теплопроводности λ и теплоемкость к в каждом зерне находятся по правилу смеси, а мощность внутреннего теплового источника у обусловливается не только теплотой фазовых превращений, но и пластическими деформациями: N1nN к9 - V ■ (X ■ V9) = ^Z, I т(k)Y(k) + ^pig,Z,,(7) i=1 k=1 где gi — скрытая теплота фазового перехода, pi — плотность материала i -й фазы. В механике сплошных сред часто возникает необходимость рассмотрения проблем, в которых те или иные характеристики исследуемого процесса позволяют выделить «плавную» — регулярную составляющую, и быстро меняющуюся — осциллирующую, части (характерный пример — турбулентные течения). При установлении связи для однотипных характеристик различных масштабных уровней температура и ее градиент на уровне представительного макрообъема представляются в виде суммы средних по представительному объему (9^ и некоторых флуктуаций 9/: 9 = ^9^+ 9/, V9 = (V9) + (V9)/, где оператор осреднения ^ обладает следующим свойством: ^9/^ = 0, ^(V6)/^ = 0. Принимается гипотеза о том, что средние значения по представительному объему в точности равны соответствующим значениям на более высоком масштабном уровне, то есть ^9^ = 0, ^V9^ = V0. Таким образом, данное разложение можно интерпретировать как возмущение температурного поля за счет флуктуации температуры на более низком уровне из-за изменения материальных свойств в представительном макрообъеме. Такое представление позволяет свести задачу теплопроводности к задаче, записанной в терминах флуктуаций температуры [21]. 3. Общая структура алгоритма реализации модели 4. Алгоритм решения задачи теплопроводности для представительного макрообъема На макроуровне I ставится и решается краевая задача. Решение краевой задачи на макроуровне I позволяет найти в каждой точке интегрирования градиент скорости перемещений, температуру и ее градиент после интегрирования уравнения теплопроводности, которые необходимы при решении задачи на следующем временном шаге. Для задачи определения НДС каждой макроскопической точке интегрирования ставится в соответствие элемент макроуровня II, который представляет собой статистическую выборку элементов мезоуровня — отдельных зерен, то есть используется прямая модель второго типа. В задаче теплопроводности применяется прямая модель первого типа, то есть каждой точке интегрирования приписывается совокупность зерен с заданным распределением ориентаций, которые, в свою очередь, аппроксимируются совокупностью конечных элементов. Для каждой из точек интегрирования макроуровня I решаются три задачи: задача теплопроводности, задача установления долей сосуществующих фаз, задача описания НДС. НДС обуславливается не только пластической и трансформационной деформациями, но и температурным режимом. Помимо этого от температуры и фазового состава зависят практически все физико-механические свойства материала. Для связывания задач нахождения НДС и температуры кристаллиты, являющиеся статистическими элементами мезоуровня в задаче определения НДС, ассоциируются с реальными зернами, имеющими конкретную геометрию. Ниже приводятся алгоритмы решения каждой из трех подзадач. При решении температурной задачи для представительного объема макроуровня каждое зерно аппроксимируется совокупностью конечных элементов. Входной информацией служит температура 0, известная для каждой точки интегрирования к моменту начала нового шага по времени из решения задачи на макроуровне I. Также требующиеся для решения краевой задачи теплофизические характеристики, а именно теплоемкость и тензор теплопроводности конкретизируются по правилу смеси для каждого зерна после нахождения объемных долей сосуществующих фаз. После установления ориентационного тензора для каждого элемента мезоуровня осуществляется переопределение тензора теплопроводности. Теплоемкость, тензор теплопроводности и мощность внутреннего теплового источника берутся одинаковыми для всех конечных элементов, покрывающих элемент мезоуровня. После решения краевой задачи получается значение температуры во всех узлах конечно-элементной сетки. Температура в конечном элементе представляет собой среднее арифметическое температур в узлах элемента. Температура в элементе мезоуровня (зерне) находится осреднением по всем элементам, аппроксимирующим зерно. Полученные значения температуры используются в качестве начальных данных при решении задачи на следующем временном шаге. Температура в каждом узле расчетной сетки задается как сумма значений на макроуровне I (0) и некоторых флуктуаций (0/): 0 = 0 + 0/. Значения величины 0 известны в каждой точке интегрирования из решения задачи на макроуровне I, поэтому уравнение теплопроводности для рассматриваемой области можно записать в терминах флуктуаций 0/: [ С 6]{0 /} + [ K 6]({0} + {0/}) + [ C в]{<0}-{W } = 0, где {0/} — вектор узловых флуктуаций температур; [С8] — матрица теплоемкости; [K8] — матрица теплопроводности; {W} — мощность внутренних тепловых источников / стоков. Из условия связи между различными масштабными уровнями следует, что среднее значение температуры и ее градиента на мезоуровне равны значениям этих величин на макроуровне: {0^ = 0, (V0) = V0 . Если воспользоваться простейшим способом осреднения — осреднением по объему, то последнее условие можно записать в следующем виде: JV0/dV =J0/n d Г = 0. V Г Поэтому при решении краевой задачи для области, представляющей собой совокупность элементов мезоуровня, граничные условия выбираются таким образом, чтобы данное равенство выполнялось. Например, можно принять, что на границе все флуктуации равны нулю, или воспользоваться периодическими граничными условиями. 5. Определение долей фаз и НДС на мезоуровне Скорость изменения объемных долей всех сосуществующих в отдельном зерне фаз устанавливается из решения кинетического уравнения (1). Значения самих объемных долей находятся из следующих конечно-разностных соотношений, которые записываются для (N -1) сосуществующих фаз (фазовая доля N -й фазы следует из условия равенства единице суммы всех долей): 7 X t + Д t zt+дt=zt-ij^ f At, f=f(z+At,z2+Atci,c2,...,6t+At,(q)t+At). U ^d^jJ Прежде, чем решать кинетическое уравнение, необходимо найти свободную энергию многофазной системы. Свободная энергия зависит: от упругой составляющей меры деформационного состояния qe ; от температуры, известной из решения задачи теплопроводности на рассматриваемом временном шаге; от концентраций легирующих элементов c1,c2,... , которые остаются такими же, как и в исходном аустените. Параметры материала в многофазной системе обуславливаются фазовым составом и рассчитываются по правилу смеси: mmmm t+A t t++A t-r-r t+A t ^t +A t t+A t ^t+A t t + A t t++ A t П = 5Z i П , a = £Z i а,, X = £Z , X, , к = £Z,к i =1 i=1 i=1 где нижний индекс «i » указывает на принадлежность величины конкретной фазе. Параметры материала отдельных фаз могут в значительной мере зависеть также от температуры, поэтому при необходимости требуется их перерасчет в соответствии с найденными значениями. На каждом временном шаге решение задачи определения НДС включает три этапа: 1) нахождение скоростей неупругих деформаций, скоростей напряжений и спинов элементов на основе разработанной модели мезоуровня; 2) процедуру интегрирования для установления параметров процесса (напряжений, изменения ориентации элементов) на конец текущего – начало следующего временного шага; 3) изменение ориентаций элементов мезоуровня. В качестве «входной» информации на каждом временном шаге выступает информация о внешнем воздействии — транспонированный градиент скорости перемещений, известный из решения задачи на макроуровне I, скорость изменения температуры (6) и температура (6), известные из решения задачи теплопроводности на рассматриваемом временном шаге. Кроме этого для решения задачи необходимо знать параметры процесса нагружения (напряжения и тензоры упругих свойств, переопределенные с учетом изменения ориентации решетки), рассчитанные на конец предыдущего шага по времени и накопленные в процессе деформирования сдвиги по системам скольжения в зерне. В результате применения модели мезоуровня на «выходе» становятся известными неупругая составляющая транспонированного градиента скорости перемещений ZП, тензор спина го и скорость изменения напряжений ст, с учетом ротаций — тензоры упругих свойств отдельных зерен. Неизвестной остается только мощность внутреннего теплового источника, которая зависит как от протекающих фазовых превращений, так и от пластической деформации (7). В качестве элемента мезоуровня рассматривается зерно. Использование в рамках модели гипотезы Фойгта (расширенной) приводит к соотношению vV = VV. Поскольку компоненты градиента скорости перемещений для представительного объема макроуровня «привязаны» к лабораторной системе координат, для задания воздействия на мезоуровне требуется их преобразование в систему координат, связанную с решеткой аустенита, так как при рассмотрении фазовых превращений все величины принято записывать в базисе родительской фазы. Система уравнений, в которую входят соотношения (2)–(6), на каждом шаге по времени разрешается в скоростях. Для упрощения записи соотношений модели мезоуровня такие величины, как тензор упругих свойств, градиент трансформационной деформации и другие записываются в системе координат, связанной с решеткой кристаллита. Кроме того, вследствие перехода к решеточному базису (аустенита), в законе Гука исчезают слагаемые (- го ■ ст), (ст ■ го), поскольку физический смысл коротационной производной есть скорость изменения компонент тензора по отношению к подвижному наблюдателю (в данном случае — связанному с решеткой аустенита). Неупругая ( ζ irn ) и термическая ( ζ trh ) составляющие градиента относительной скорости перемещений в многофазной системе устанавливаются из уравнений: {ZП}t+At = £ Z ‘+At£Yt ^tb(k)n(k)+£Zi {f *}t+At, i k=i i {z th} t+At = at+At 6 . При этом скорости сдвига вычисляются как • t +A t _ •(k) rr ( t+A t _ t+A t \ Y(k)i =Y0i H (T(k)iTc(k)i ) t+A t T( k )i t+A t 1c (k) i 1/ mci . Здесь t+A t τ c (k) A = Tt x + T(k) c (k) A cA 0 j=1 r V t+At YA (j) n 5 Ytj ^A A YA (j) — BAθt t *- c (k) A m 2A —1 J n у v t+At (k) £ YA (j)+g А . j=1 Тензор спина решетки рассчитывается с помощью соотношения: ω t+ A t 1 // «-.V+A t = — (vv ) N1 n -(vv) t+At)-1 Ze;- Zt (:? (ь'k 'n'k ’-nik ’ь ik ’). 7 2 i=1 k=1 Далее осуществляется интегрирование соотношения (6) по известным транспонированному градиенту относительной скорости перемещений и его неупругой и термической составляющим. В результате в системе координат, связанной с решеткой аустенита, находятся напряжения на конец данного временного шага: (c)t+At = (c)t + П : (Zr -zin -Zth ’At. Для интегрирования соотношения ю = 0) ■ oT(o — ориентационный тензор зерна, характеризующий положение его кристаллографической системы координат по отношению к лабораторной системе координат и переводящий лабораторную систему координат в систему координат, связанную с решеткой аустенита) применяется следующий алгоритм: – определяется вектор угловой скорости χ как ассоциированный вектор для тензора спина ω — Xt = (G : юt ’/1 (С — тензор Леви-Чивиты); - по X находятся единичный вектор оси скорости (приращения) поворота e = (Ar/1Ar|) (Ar = (xt + Xt+At ’a1jl) и угол Аф, на который необходимо повернуть решетку из текущего положения; - по вычисленным значениям компонент вектора e, относительно которого тензор ротации AR поворачивает решетку, и угла такого поворота Аф восстанавливается ортогональный тензор ротации ARt = cos АфtI + (1 + cos Афt ’ ee + sin Афte x I; - с учетом нового значения тензора ротации переопределяется ориентационный тензор o*+Аt = AR ■ ot, то есть явные внутренние переменные из системы координат, связанной с решеткой аустенита, преобразуются в лабораторную систему координат. 6. Решение температурной задачи на макроуровне I Мощность внутреннего теплового источника вычисляется как m1n m2 _t+At X4t+AtV,t+At-t+At , V* _ _ y L- LTk/у(k'i+LPigi-■ i=1 k=1 i =1 Решение уравнения теплопроводности для представительного макрообъема дает на «выходе» для каждой точки интегрирования значения параметров и характеристик, входящих в уравнение теплопроводности макроуровня I, а именно коэффициента теплоемкости, тензора теплопроводности, мощности внутреннего теплового источника: К t+At к t+At Использование метода конечных элементов позволяет свести температурную задачу на макроуровне I к следующей системе алгебраических уравнений: [ C *6]{®}+[ K *6]{®}+{^ *} = 0, где {©} — вектор узловых температур физического тела; Nинт [с*6] = А [ V£ [ф(n’] кt+Аt (n )[ф(п)] матрица теплоемкости; Nинт [K^ = А ^ V £ [B (п ’] [лt+Аt (п)] [B (п,)] [+А I i=1 J h [ф]т [ф] dГ > Г8/Q матрица Nm I теплопроводности; {^} = АI-V £[ф( п’] {у*+А t (п’}[+А [J q [ф] d г-J h @„[ф] > i=1 т г вектор |Г q Ге/q тепловой нагрузки; [ф] — матрица функций формы; [B] — матрица производных функций формы; Nинт — количество точек интегрирования в конечном элементе; А — символ операции ансамблирования; V — объем конечного элемента; К(nij, [Л (nij], Y (nij — значения теплоемкости, элементов матрицы коэффициентов теплопроводности и мощности внутренних сил соответственно, известные в каждой точке интегрирования после решения задачи для представительного объема макроуровня; ГG — часть границы, на которой задается проекция вектора теплового потока на внешнюю нормаль; Г0/G — часть границы, на которой задается условие теплообмена с окружающей средой по закону Ньютона; h — коэффициент теплообмена; 0у— температура окружающей среды. 7. Задача определения НДС на макроуровне I В результате решения задачи нахождения НДС на мезоуровне в каждой точке интегрирования становятся известными тензор упругих свойств Пt+Дt = (S : nt+Дt \, тензор спина Qt+Дt = (гоt+Дt), неупругая составляющая градиента относительной скорости перемещений (t+Дt —1 t+Дt t+Дt / / \t+Дt t+Дt —1 t+Дt / / \t+Дt / / \t +Дt / / \t +Дt 7 m t+Д t / in / / / t+Д t / / / / Zr ) =(П ) : \S : ( П ) : ^ Г j j б) (П j ' ' j j j j t+Д t \ / / ! * \t+Д t \ +{(£ in j ) + ((a / 9 j } , входящие в закон Гука, который затем используется при решении краевой задачи на макроуровне I. Уравнение равновесия на макроуровне I при переходе к конечно-элементному виду сводится к следующей системе алгебраических уравнений ([ K- ]+[ K vv ]+[ K3v ]+[ Kv ]}{V} t+Д t = {R} t+Д t. Здесь {V} — вектор узловых скоростей физического тела; [ф] — матрица функций формы; [B- стандартная конечно-элементная B-матрица; [K1- ] = А I 1=1 жесткости; {R} = A|v^{[B-(n,)]T [П(n J]t-*t ({Z- (n j}t•*t + Q(n, )}+{zth (nj}t-t j+[B'(n j]'[T(n j]■ “■ {Z(n j|t-}}+ l i=1 +А j J [ф]' {T}dГ + J [ф]' {li} dV ■ — вектор нагрузок; In(ni j], {Zin (ni j}, {Q(ni j} — матрица упругих l Гs Ve свойств, векторы неупругой составляющей градиента относительной скорости перемещений и спина, установленные в каждой точке интегрирования; {T} — вектор поверхностных сил; {В} — вектор объемных сил; rz — часть границы, на которой задаются силовые граничные условия; ■ 0 0 0 -2Q12 -2Q13 0 " 0 0 0 2Q12 0 -2Q23 [ T1 ] = 0 Q12 0 12 0 0 0 0 2Q13 -^23 2Q23 -Qn . Учет нелинейности обусловил появление матриц IK- ], ^13 0 —Q13 ^23 0 -Q12 [ 0 ^23 —Q23 ^13 ^12 0 J Kз- ], IK- ] которые не обладают свойством симметрии и находятся следующим образом: IK- ] = А НIB- ]' {I} {S}' [B- ] dV}; IK- ] = А И [ф]' {В} {I}' IBv ] dV\; l Vs l Vs„ IK- ]=АIJ [ф]' ({T} {I}T — {N}{N}' {N} {Z}' IBv ] dг) I. lr= Приведенный алгоритм реализован в виде вычислительной программы на языке программирования FORTRAN. В задаче теплопроводности предусмотрена возможность распараллеливания процесса решения на машине с несколькими процессорами с использованием технологии OpenMp. 8. Обсуждение результатов С помощью программы, созданной на основе разработанного алгоритма, осуществлено численное моделирование деформирования представительного объема макроуровня при одноосном растяжении, Рис. 1. Расположение осей лабораторной системы координат ( 1A , 2A , 3A ) и схема перестройки решетки ГЦК в решетку ОЦК простом сдвиге и сложном нагружении (растяжении–сдвиге, сдвиге–растяжении). Аналогично деформировался образец и при натурных испытаниях. Представительный объем состоял из 3375 зерен, шаг интегрирования по времени составлял 0,05 с. На рисунке 1 показано расположение осей лабораторной системы координат. Во всех вычислительных экспериментах в качестве моделируемого материала принималась сталь AISI 301, физические свойства которой можно найти на сайте Расчеты проводились для комнатной температуры, при этом полагалось, что изменение температуры образца может происходить за счет пластической деформации аустенита и мартенсита, а также протекающих фазовых превращений. Параметры модели для описания поведения стали AISI 301 брались такими же, как и параметры для стали AISI 304, которые найдены ранее. Рис. 2. Кривая «интенсивность деформаций–интенсивность напряжений» для случая одноосного растяжения (а) и простого сдвига (б): расчет (кривая 1); эксперимент (2) ст„ МПа Для обоснования возможности использования выбранных параметров проводились численные эксперименты на одноосное растяжение и простой сдвиг и полученные зависимости «интенсивность деформаций–интенсивность напряжений» сравнивались с экспериментальными кривыми [22]. На рисунке 2 представлены результаты натурного эксперимента и кривая, построенная по расчетным данным. Максимальное отклонение вычисленной кривой от экспериментальной составляет порядка 8% для одноосного растяжения и 10% для простого сдвига. Рисунок 3 содержит зависимость относительной объемной доли мартенсита, образовавшегося в процессе превращения, от интенсивности деформаций при простых видах деформирования. Здесь относительная объемная доля мартенсита есть отношение суммы объемов всех вариантов мартенсита к рассматриваемому объему материала. В случае одноосного растяжения при жестком нагружении известной являлась только одна компонента градиента скорости перемещений Z11 = 1,3-10-4с-1; кроме того, все компоненты тензора Ё1у, за исключением Ё 11, были нулевыми; остальные компоненты градиента скорости перемещений и компонента тензора Ё 11 находились из решения системы Рис. 3. Зависимость доли образовавшегося мартенсита от интенсивности деформаций: одноосное растяжение (кривая 1); простой сдвиг (2) алгебраических уравнений, построенной на основе закона Гука. При моделировании простого сдвига реализовано жесткое нагружение Z12 =-0,5 -10-5с-1, Zj = 0, (ij) ^ (12). Предполагалось, что в процессе деформирования может образовываться мартенсит трех разновидностей, соответствующих трем возможным деформациям Бейна [23]. Для анализа процессов деформирования и фазовых превращений на мезоуровне рассматривалось два положения зерна: зерно благоприятно и неблагоприятно ориентированное по отношению к внешней нагрузке (вид деформирования — одноосное растяжение). Для пояснения термина «благоприятная ориентация» следует обратиться к рисунку 1: если тетрагональную ячейку сжимать вдоль направления [001]γи одновременно растягивать по направлениям 110 , то ее тетрагональность будет уменьшаться и в пределе получится ячейка ОЦК решетки. Экспериментально показано, что наибольшее количество мартенсита в зерне образуется в том случае, если ось сжатия решетки соответствующей разновидности мартенсита близка к направлению приложения нагрузки; в расчетах оказалось, что для одного из зерен система координат, связанная с решеткой аустенита, практически совпадает с лабораторной системой координат. На рисунках 4 и 5 приведены зависимости долей каждого из трех вариантов образовавшегося мартенсита и интенсивности напряжений от интенсивности деформаций для обоих зерен. а 0,05 0,10 0,15 е, 0 0,05 0,10 0,15 Е, Рис. 4. Зависимость долей ^ образовавшихся разновидностей мартенсита от интенсивности деформаций е, для зерна с благоприятной (а) и неблагоприятной (б) ориентацией: доля первого (кривая 1); второго (2); третьего (3) вариантов мартенсита а,, МПа / 0 0,05 0,10 0,15 е, Рис. 5. Кривая «интенсивность деформаций– интенсивность напряжений» для случая одноосного растяжения; ориентация зерна благоприятная (кривая 1) и неблагоприятная (2) Из рисунка 4 видно, что при благоприятной ориентации зерна наибольшее количество мартенсита образуется, если ось сжатия решетки соответствующей разновидности мартенсита близка к направлению приложения нагрузки. Доли двух остальных вариантов мартенсита практически одинаковы. При неблагоприятной ориентации зерна нельзя выделить вариант мартенсита, который имеет преимущество, так как их доли отличаются незначительно. Расчеты показали (см. Рис. 5), что в зерне с благоприятной ориентацией уровень напряжений выше, что может быть связано с увеличением объемной доли жесткой мартенситной фазы, обладающей высоким пределом текучести (подобная зависимость, конечно же, не всегда справедлива, так как напряжения могут расти и за счет взаимодействия с соседними зернами, имеющими различные ориентации). При сложном нагружении рассмотрены следующие процессы деформирования: «растяжение–сдвиг» для различных уровней предварительной деформации (0,068; 0,085), а также процесс с обратным порядком нагружения, то есть «сдвиг–растяжение». На рисунках 6 и 7 приведены зависимости интенсивности напряжений и относительной объемной доли образовавшегося мартенсита от интенсивности деформаций для трех названных выше процессов деформирования. Как видно из рисунка 6, после излома траектории деформирования наблюдается характерное снижение интенсивности напряжений. Можно отметить, что при изменении уровня предварительной деформации характер зависимости интенсивности напряжений от интенсивности деформаций не меняется, остается практически одинаковый относительный объем образовавшегося мартенсита. Также следует отметить, что во всех трех процессах относительный общий объем образовавшегося мартенсита меньше, чем Рис. 6. Кривая «интенсивность деформаций–интенсивность напряжений»: растяжение (до интенсивности 0,068)–сдвиг (кривая 1); растяжение (до интенсивности 0,085)–сдвиг (2); сдвиг (до интенсивности 0,068)–растяжение (3) Рис. 7. Зависимость относительной объемной доли мартенсита от интенсивности деформаций: растяжение (до интенсивности 0,068)–сдвиг (кривая 1); растяжение (до интенсивности 0,085)–сдвиг (2); сдвиг (до интенсивности 0,068)–растяжение (3) и при одноосном растяжении, и при простом сдвиге. Возможно, основное влияние на наблюдаемые зависимости оказывают процессы разворотов кристаллических решеток зерен и изменение микроструктуры. После излома траектории из-за появившегося изменения микроструктуры материала скольжение по некоторым системам замораживается, а вместо этих систем включаются другие. Можно предположить, что после увеличения продолжительности первого участка траектории деформирования (деформирование идет до большего значения интенсивности деформаций) необходимо большее время на стабилизацию процесса, вследствие чего интенсивность напряжений в этом случае меньше. Тот факт, что ни в одном из процессов деформирования объем образовавшегося мартенсита не достигает значений, полученных при простом нагружении, можно объяснить тем обстоятельством, что на первом участке траектории деформирования разворот кристаллических решеток может привести к появлению преимущественного направления. Поэтому при смене траектории деформирования рост объема мартенсита менее интенсивен, чем в случае простого нагружения. 9. Заключение Предложена модель поведения сталей при термомеханическом нагружении с учетом мартенситных превращений. Для облегчения постановки и решения связанной задачи последняя представляется совокупностью трех подзадач: теплопроводности, определения НДС и нахождения объемных долей сосуществующих фаз. В статье представлено подробное описание алгоритма реализации модели для всех трех подзадач на двух масштабных уровнях. С использованием разработанного алгоритма выполнены численные эксперименты и проанализированы результаты расчетов при простом и сложном нагружениях представительного объема макроуровня. В случае простого нагружения следует отметить приемлемое согласование результатов вычислений с экспериментальными данными; в случае сложного нагружения сравнение результатов численного эксперимента с данными натурных экспериментов не проводилось в силу отсутствия последних. Работа выполнена при финансовой поддержке РФФИ (проект № 13-01-96006-р_урал_а) и Правительства Российской Федерации (Постановление № 220 от 9 апреля 2010 г.; договор № 14.В25.310006 от 24 июня 2013 года).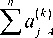
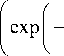
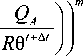
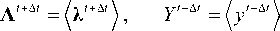
Список литературы Двухуровневая модель для описания поведения сталей при термомеханическом нагружении с учетом мартенситных превращений: алгоритм реализации модели
- Loginova I., Agren J., Amberg G. On the formation of Widmanstäten ferrite in binary Fe-C-phase-field approach//Acta Mater. -2004. -V. 52, N. 13. -P. 4055-4063.
- Steinbach I., Apel M. Multi-phase field model for solid state transformation with elastic strain//Physica D. -2006. -V. 217, N. 2. -P. 153-160.
- Artemev A., Jin Y., Khachaturyan A.G. Three-dimensional phase field model and simulation of cubic → tetragonal martensitic transformation in polycrystals//Philos. Mag. A. -2002. -V. 82, N. 6. -P. 1249-1270.
- Wang Y., Khachaturyan A.G. Three-dimensional field model and computer modeling of martensitic transformations//Acta Mater. -1997. -V. 45, N. 2. -P. 759-773.
- Yamanaka A., Takaki T., Tomita Y., Yoshino M. Crystal plasticity phase-field simulation of deformation behavior and microstructure evolution in polycrystalline material//Proc. of X Int. Conf. on Computational Plasticity. COMPLAS X, Barselona, Spain, September 2-4, 2009. -P. 1-4.
- Tjahjanto D.D., Turteltaub S., Suiker A.S.J. Crystallographically based model for transformation-induced plasticity in multiphase carbon steel//Continuum Mech. Therm. -2008. -V. 19, N. 7. -P. 399-422.
- Turteltaub S., Suiker A.S.J. A multiscale thermomechanical model for cubic to tetragonal martensitic phase transformations//Int. J. Solids Struct. -2005. -V. 43, N. 14-15. -P. 4509-4545.
- Yadegari S., Turteltaub S., Suiker A.S.J. Coupled thermomechanical analysis of transformation-induced plasticity in multiphase steels//Mech. Mater. -2012. -V. 53. -P. 1-14.
- Lee M.-G., Kim S.-J., Han H.N. Crystal plasticity finite element modeling of mechanically induced martensitic transformation (MIMT) in metastable austenite//Int. J. Plasticity. -2010. -V. 26, N. 5. -Р. 688-710.
- Mahnten R., Schneidt A., Antretter T. Macro modeling and homogenization for transformation induced plasticity of a low-alloy steel//Int. J. Plasticity. -2009. -V. 25, N. 2. -P. 183-204.
- De Oliveira W.P., Savi M.A., Pacheco P.M.C.L., de Souza L.F.G. Thermomechanical analysis of steel cylinders quenching using a constitutive model with diffusional and non-diffusional phase transformations//Mech. Mater. -2010. -V. 42, N. 1. -P. 31-43.
- Трусов П.В., Ашихмин В.Н., Волегов П.С., Швейкин А.И. Определяющие соотношения и их применение для описания эволюции микроструктуры//Физ. мезомех. -2009. -Т. 12, № 3. -С. 61-71.
- Трусов П.В., Ашихмин В.Н., Швейкин А.И. Двухуровневая модель упругопластического деформирования поликристаллических материалов//Механика композиционных материалов и конструкций. -2009. -Т. 15, № 3. -С. 327-344.
- Поздеев А.А., Трусов П.В., Няшин Ю.И. Большие упругопластические деформации: теория, алгоритмы, приложения. -М.: Наука,1986. -232 с.
- Исупова И.Л., Трусов П.В. Математическое моделирование фазовых превращений в сталях при термомеханической нагрузке//Вестник ПНИПУ. Механика. -2013. -№ 3. -С. 126-156.
- Трусов П.В., Швейкин А.И. Многоуровневые физические модели моно-и поликристаллов. Статистические модели//Физ. мезомех. -2011. -№ 4. -С. 17-28.
- Трусов П.В., Швейкин А.И. Многоуровневые физические модели моно-и поликристаллов. Прямые модели//Физ. мезомех. -2011. -Т. 14, № 4. -С. 5-30.
- Трусов П.В., Нечаева Е.С., Швейкин А.И. Применение несимметричных мер напряженного и деформированного состояния при построении многоуровневых конститутивных моделей материалов//Физ. Мезомех. -2013. -Т. 16, № 2. -С. 15-31.
- Трусов П.В., Волегов П.С. Физические теории пластичности: приложение к описанию упрочнения в поликристаллах//Вестник Тамбовского университета. Серия: Естественные и технические науки. -2010. -Т. 15, № 3-1n. -С. 983-984.
- Трусов П.В., Швейкин А.И., Нечаева Е.С., Волегов П.С. Многоуровневые модели неупругого деформирования материалов и их применение для описания эволюции внутренней структуры//Физ. мезомех. -2012. -Т. 15, № 1. -С. 33-56.
- Özdemir I., Brekelmans W.A.M., Geers M.G.D. Computational homogenization for heat conduction in heterogeneous solids//Int. J. Numer. Meth. Eng. -2008. -V. 73, N. 2. -P. 185-204.
- Beese A.M. Experimental investigation and constitutive modeling of the large deformation behavior of anisotropic steel sheets undergoing strain-induced phase transformation/PhD Dissertation in Mechanical Engineering. -Massachusetts Institute of Technology, 2011. -146 p.
- Cho J.-Y. Finite element modeling of martensitic phase transformation/PhD Dissertation in Mechanical Engineering. -Texas Tech University, 2009. -109 p.


