Двухуровневая оптимизация перестановки сенсоров

Современные методы хранения, обработки и интеллектуального анализа больших объемов информации, полученной с помощью сенсоров, предоставляют богатые возможности для различных отраслей науки и промышленности, помогая делать новые выводы и углублять понимание природы известных явлений, отслеживать динамику важных параметров и предупреждать нежелательное развитие событий, обеспечивать безопасное и сбалансированное развитие технологий.

Размещение сенсорных устройств на больших площадях связано с существенными трудозатратами, которые многократно возрастают в случае, когда, устройства, требуется периодически перемещать для увеличения достоверности наблюдений. При проведении таких регулярных перемещений даже небольшой выигрыш в каждом конкретном маршруте приводит к ощутимой экономии сил и средств в ходе всего измерительного эксперимента.

В настоящей статье будет рассмотрена, двухуровневая задача, оптимизации перемещений при планировании эксперимента, связанного с использованием сенсорных устройств. Первый уровень предполагает оптимизацию движения агента, при перестановке сенсоров с текущих позиций на новые заданные (задача, известна в литературе как 1-PDTSP [1-3]) (см. рис. 1). В предшествующей работе автора [4] для данной задачи был предложен специальный метод динамического программирования (МДП).

Второй уровень оптимизации связан выбором наилучшего порядка на множестве самих расстановок. Предполагается, что на этапе планирования эксперимента заранее выбирается множество наборов позиций в соответствии с содержательными требованиями измерительной задачи. На позициях из каждого набора сенсоры остаются в течение некоторого времени, после чего перемещаются на позиции следующего набора. В случае, если на порядок следования наборов позиций в ходе замеров не накладывается ограничений из содержательных условий задачи, можно сформулировать задачу оптимизации этого порядка в смысле совокупных трудозатрат (см. рис. 2).

Рис. 1. Допустимые (А и В) и недопустимые (С и D) маршруты в задаче перестановки 3 сенсоров (черные точки) на новые позиции (выколотые точки)

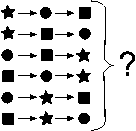
Рис. 2. Внешняя задача: выбор оптимального из 6 возможных порядков, в которых могут следовать 3 расстановки

1.    Дискретизация карты

Пусть задана дискретизация некоторой карты местности в виде взвешенного неориентированного графа (целочисленной решетки) G = ( V, E ), каждая « внутренняя » вершина которого имеет степень 4, каждая « угловая » - 2, а остальные - 3. Весом w : E ^ R всякого из ребер этого графа будем считать трудоемкость перемещения между инцидентными данному ребру вершинами. Вообще говоря, граф может моделировать неоднородную местность, соответственно ребра графа могут значительно различаться по весу (см. рис. 3).

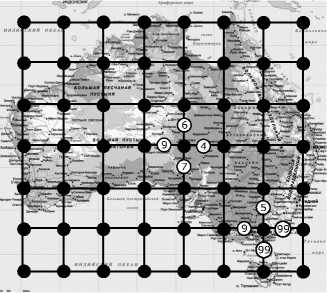
Рис. 3. Пример графа, обеспечивающего дискретизацию карты местности. Перемещение по горам более затратно, чем по равнине, кроме того, за счет выбора весов ребер ограничены переходы между сушей и морем

Далее мы считаем, что сенсоры могут размещаться лишь в вершинах графа. Для каждой пары ( v 1 , v 2) Е V ² определим стоимость перемещения

d : V ² ^ R                                 (1)

как кратчайший путь между этими вершинами в графе. Для решения задачи нахождения кратчайшего пути можно использовать, например, алгоритм Дейкстры (подробнее см. обзор [5]).

2.    Внутренняя задача перестановки

Как уже отмечалось выше, в большинстве случаев измерительный эксперимент позволит получить более достоверные данные, если доступные исследователю n сенсоров периодически перемещать на новые позиции изучаемой области. Итак, в ходе эксперимента целесообразно периодически переставлять n сенсоров на n новых позиций. Мы предполагаем, что n << |V ² | и считаем, что сенсоры взаимозаменяемы, то есть любой сенсор может одинаково эффективно функционировать на любой из позиций. Среди вершин графа выделим множество точек, в которых допустим старт и финиш V С V. Содержательно множество V определяется наличием возможности подъезда (подхода). Так, например, естественно потребовать, чтобы маршрут каждой перестановки начинался и заканчивался на дороге, с которой работника может забрать транспорт; в данном случае точки V , соответствующие дороге, составят множество V.

Приведем строгую постановку задачи. Введем 2 n -элементное множество X = {v 1 ,... ,v ₂ n} С V , точку старта s Е V и точку финиша e Е V. Определим, кроме того, X о , X U {s,e} . Пусть X 1 , {v 1 ,..., vn} С X есть множество позиций, с которых сенсоры необходимо собрать, а X ₂ , {vn ₊₁ ,..., v ₂ n} С X есть множество позиций, на которые собранные сенсоры следует установить. Напомним, что на элементах множества X ₀ х X ₀ задана функция стоимости перемещения (1).

Пусть функция f : P ( X ) ^ N показывает число сенсоров, оставшихся в наличии у осуществляющего перестановку агента, после того как, стартуя из точки s, агент посетил некоторый произвольный набор K С X позиций, собрав сенсоры на всех позициях X 1 П K II установив на всех позициях X ₂ П K:

{ 0 ,        если K = 0:

{ — 1 , если v Е X ₂:

1 , если v Е X 1.

^                               I ( v ) =

) , I ( v ) , иначе:                          ^{v 1}

v ∈ K

Здесь функция I определяет, что а) при посещении каждого установленного сенсора происходит его изъятие (число сенсоров у агента увеличивается на 1); б) при посещении каждой позиции для установки происходит размещение сенсора (при этом число сенсоров у агента уменьшается на 1).

Всякий кортеж ( x 1 ,..., xk ) Е Xk, г де к Е 1 , 2 n , будем называть допустимим, если справедливо условие

^j Е 1 , k f ( {x i , ...,Xj } ) >  0;

-

в этом случае « расширенный » кортеж ( s, x 1 , ...,x _k , e ) также будем называть допустимым.

-

Введенных обозначений достаточно, чтобы сформулировать постановку внутрен ней оптимизационной задачи: требуется найти перестановку y0 : 1, 2n о 1, 2n, на которой достигается

(2 п-1\

V d(vy(i) v(i+1)) + d (vy(2n) ,e) ^ min,(2)

γ∈G i=1/ где

G , Щ: 1 , 2 n о 1 , 2 n | ( V y (1) ,..., V y (2 n )) - допустим }.

Здесь условие (2) обеспечивает минимальность « трудоемкости » выбираемой очередности посещения сенсоров и позиций для установки в смысле заданной функции стоимости перемещений d, а условие (3) не допускает ситуации, в которой агент прибыл на позицию для установки, не имея в наличии сенсоров.

Для решения каждой единичной задачи перестановки, являющейся, фактически, частным случаем задачи 1-PDTSP, можно использовать как ряд известных методов [1-3], так и предложенный ранее автором [4] специальный вариант метода динамического программирования, который будет далее рассмотрен для полноты изложения кратко и без доказательства:

\ I d ( s,x ) , если I ( x ) = 1;

Vx G X v (0 , x ) =

H, иначе;

VK С X :1 < |K| < |X|, Vx G X \ K min{d(У, x) + v(K \ {У} У)} если f(К U {x}) > 0:         (5)

v ( K, x )= y^K

H,                          иначе:

v(X,e) = min{d(y.e) + v(X \ {У}.У)} y∈X где H некоторое достаточно большое число, например. H = 2 ^ d(x, У)•

Для восстановления очередности посещения элементов X используется обычный для динамического программирования алгоритм, действующий «в обратном порядке»:

• 1)    пусть z 2 n G X такой, что при y = z 2 n выражение (6) достигает своего минимума;

• 2)    при x : = z 2 n, K : = X \ {z 2_n } выберем z 2 n- 1 G K так. чтобы при y = z 2 n- 1

выражение (5) достигало своего минимума;

• 3)    при x := z 2 n- 1 , K := X \ {z 2 n,z 2 n— 1 } выберем z 2 n— 2 G K так. чтобы z 2 n—- 2

минимизировал выражение (5);

2n) при x := z ₂ , K := X \ {z ₂ n,..., z ₂ } z 1 G K определяется единственным образом.

В результате применения описанной процедуры восстановления получим допустимый кортеж ( z 1 , ...,z _{2 n} ). Пусть y 0: 1 , 2 n о 1 , 2 n есть взаимно однозначное отображение индексов такое, что Vi G 1 , 2 n zi = v _{Y ь}( i ), тогда y 0 является искомым решением задачи (2),(3): y 0 = Y 0' Трудоемкость приведенного метода решения не отличается от трудоемкости стандартного метода динамического программирования: O ( n 22 ⁿ ).

Введем обозначения для решения единичной внутренней задачи перестановки с оптимально выбранными точками старта и финиша

D ( X i ,X 2)= min F ( s,e,X 1 ,X 2) .                      (7)

( s,e ) ∈ V ²

В большинстве прикладных постановок эту задачу можно решить перебором, сужая по необходимости множество V. Отметим, что точка старта и точка финиша могут совпадать s = e Е V (случай, когда работник прибыл на собственном транспортном средстве и должен вернуться к нему после окончания работ), либо различаться (после окончания работ в любой точке множества V работник может быть подобран в любой доступной для транспорта точке).

3.    Внешняя задача оптимизации порядка перестановок

Пусть у исследователя имеется набор расстановок сенсоров { {x 1 , ...,x П},..., {xM ,...,xM} }, где Vi Е 1 , n Vj Е 1 , M xj Е V , сформированный заранее с учетом эмпирических предпочтений к выбору позиций для измерения (далее Yj , {x { , ...,xn} ). Предполагается, что сенсоры находятся на позициях каждого набора в течение некоторого времени, после чего перемещаются к позициям следующего не использованного ранее набора. Для каждой упорядоченной пары ( Yi,Yj ) с помощью решения соответствующих задач (2), (3), (7) может быть рассчитана функция стоимости перестановки сенсоров с позиций {xi,...,х^г _п } на позиции {x { , ...,xn} . Используя введенные обозначения, сформулируем внешнюю задачу поиска оптимального порядка следования расстановок в виде классической задачи коммивояжера:

• 1)    минимизация совокупных затрат

M - 1

У D ( Yф ( i ) , Yф ( i +1)) ^ _min_;                        ( 8 )

^—^                       ф : 1 ,М о 1 ,М

• 2)    постановка «на узкие места»

4.    Вычислительный эксперимент

max _{ D ^{( Y}ф ( i ) ^,Yф ( i +1))} ^    min .                       (9)

iE 1 ,M- 1                           ф : 1 ,Mо 1 ,M

Насколько известно автору, подобная задача оптимизации порядка расстановок ранее не рассматривалась в литературе. В следующем разделе приводятся результаты вычислительного эксперимента, демонстрирующего влияние внешней оптимизационной компоненты двухуровневой задачи (в форме (8)) на совокупные трудозатраты в процессе измерений с периодическим перемещением сенсоров.

В ходе вычислительного эксперимента решалась задача (8) при условии, что вершина старта совпадает с вершиной финиша и располагается в угловой точке V = { (1 , 1) } дискретной сетки V = 1 , 100 х 1 , 100. Позиции для сенсоров равновероятно выбирались среди элементов V . Серии повторяющихся единичных экспериментов проводились для числа сенсоров n = 5 и различного количества расстановок M с целью оценить динамику изменения влияния внешней оптимизационной компоненты (8) на трудоемкость модельных наблюдений при росте числа расстановок.

В каждом k -том единичном эксперименте M наборов по 5 позиций случайным образом размещались на вершинах сетки V: {Y 1 = {x 1 , ...,x 5 },..., Y _M = {xM,... ,x M} }. Для каждой упорядочен ной пары наборов позиций ( Yi,Yj ) с помощью (4) - (6) оптимально решалась задача перестановки сенсоров с позиций {^x 1 , . . . , ^x 5 } И ^-I¹ позиции {x 1 ,... ,x 5 } . Полученные значения определяли функцию D из (7) (в данном случае s = e = (1 , 1)). после чего:

• 1)    оптимально решалась задача (8) с результирующим значением минимума. Hk ( M ):

• 2)    рассчитывалась совокупная трудоемкость перестановок без оптимизации второго уровня Hk ( M ) = £ iM- ¹ D ( YiY +1);

• 3)    результатом единичного эксперимента считался коэффициент ck ( M ) = H 0( M ) /Hk ( M ) .

Для всякого значения M Е { 5 , 10 , 15 , 20 , 25 } единичный эксперимент повторялся 100 раз, позволяя вычислить усредненный коэффициент (см. рис. 4)

c ( M Е Ck ( M ) .                       U0)

к =1

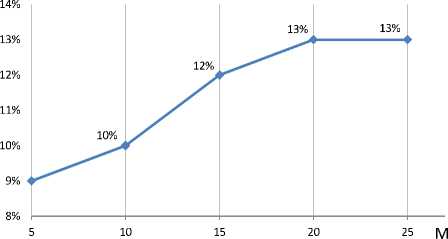
Рис. 4. Зависимость относительного выигрыша (10) в трудоемкости совокупных перемещений при использовании пяти сенсоров от числа перестановок M

Заключение

В работе исследовано влияние оптимизации порядка, в котором сменяют друг друга, группы позиций сенсоров, на совокупную трудоемкость перемещений при проведении измерительных работ. Полученные в ходе эксперимента результаты показывают, что даже при небольшом числе сенсоров (в проведенных экспериментах 5) и относительно небольших количествах перестановок, оптимальное решение внешней задачи позволяет добиться существенного (до 13 %) выигрыша в трудоемкости по сравнению со случайным порядком следования перестановок. В дальнейшем предполагается численно исследовать влияние на трудоемкость эксперимента внутренней задачи оптимизации маршрута, перестановки сенсоров (в сравнении с аналогичной маршрутной задачей, решаемой человеком [6]), использовать приближенные к реальности модели карт местности ( V, d ) и существенно расширить вычислительный эксперимент.