Двухволновое приближение при дифракции света на бинарной диэлектрической решетке

Рассмотрим диэлектрическую бинарную дифракционную решетку (рис. 1) периодическую вдоль оси x, штрихи которой направлены вдоль оси y. Пусть на такую решетку падает плоская волна под углом 9 в плоскости (x,z) и электрический вектор линейно - поляризованной волны направлен вдоль оси y (случай ТЕ - поляризации). Тогда векторная задача полностью решается с помощью уравнения Гельмгольца для электрического вектора E(x,y)ey:

d2 E (x,z) d2 E (x,z)

+           + k e (x,z) E (x,z ) = 0,(1)

dx2d где ey - единичный вектор вдоль оси y, k=2n/X - волновое число, 8(x,z) - функция относительной диэлектрической проницаемости решетки в зоне модуляции рельефа (зона 2 на рис. 1), которую удобно представить в виде ряда Фурье:

^£ ( x , z ) = £ + ( £ 3 ^- £ ) £ C n ⁽ z ) exp f i^ ^ hx- 1 ,    ⁽²⁾

h =-^           \ T /

cr„_r = k sin 0 - n K , nx

^ nz = k ^[ £ 0 — £ 1 sin² 0 ^{] /2}

8 ₀ - среднее значение диэлектрической проницаемости в зоне 2 модуляции рельефа решетки.

Подставляя разложения (2) и (3) в уравнение (1), получим систему дифференциальных уравнений для амплитуд дифракционных порядков решетки:

d ² S„ ( z )

n   - 2ikl£n - £ Sin 0 lx dz2            0    1

x /2 ^ⁿz + к ² n ( m - n ) S „ ( z ) +              (4)

dz

+ k ² ( £ 1 - £ 3 ) £ [ CS - 1 ( z ) + Ci S n + 1 ( z ) ] = 0.

1 = 1

Для бинарной решетки Cl не зависят от z и

a a J ^£ 0 = ^£ 3 t ⁺ l ^{1 -} t J ^£ 1 ,

2 T Jas sin 0

m =--------

число

где 8 1, 8 3 - диэлектрические проницаемости окружающей среды и материала решетки, T =2 n /K - период решетки с волновым числом K. Если решетка бинарная, то Cn ( z ) не зависит от z , и для бинарных решеток с одним скачком рельефа на периоде коэффи-

циенты разложения равны

C

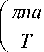
Брегга. Если m =1, то говорят, что выполняется условие Брегга. Систему уравнений (4) можно решать методом собственных функций (модовый подход) [1].

При условии, что период решетки T близок к длине волны X , в решетке возбуждаются только два дифракционных порядка, что следует из уравнения для угла наклона дифракционного порядка 9 n:

тг

Ja s sin 0 - Ja s sin 0_n

= n — .

T

где a - величина ступеньки рельефа решетки.

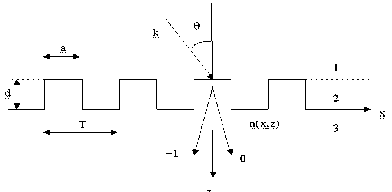
Рис. 1. Схема дифракции плоской волны на бинарной диэлектрической решетке.

При условии T »X внутри зоны модуляции будут эффективно возбуждаться только две волны S ₀(z) и S ₁(z). Тогда система уравнений (4) в двухволновом приближении запишется в виде:

.S 1 + a S 1 + n S 1 = y S ₀

• •                  •

S 0 + a S 0 = Y S 1

Комплексную амплитуду электрического вектора светового поля в зоне модуляции рельефа решетки можно представить в виде разложения по дифракционным порядкам решетки (разложение Ре-лея):

где

& &  d ² S 1,0   & _ ^dS 1,0      ‘ _ z

¹⁰ "  dz" dz' ’ z " T

a = - i 4 n^ ( £ 0 - £ 1 sin 0 ) ¹², ^ = 2 ,

П = 4 n ² ( m - 1 ),

Y = ^{- 4 n2}^ ² ( ^£ з ^{- £} 1 ^{) c} 1 ,

где

”

E (x, z )=£ Sn (z e^x' '), n =1

C 1 =

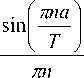
a J a)

^£ 0 = ^£ з T ^{+ £} 1 | ^{1 -} T I"

Заметим, что система уравнений (6) аналогична системе уравнений, описывающей дифракцию света

на объемных голограммах, впервые рассмотренную Когельником [2].

Пренебрегая отраженным от решетки излучением, граничные условия для системы (6) можно выбрать в виде:

S 0 ( z = 0 ) = 1, S 1 ( z = 0 ) = 0.                    (7)

Общее решение системы уравнений (6) будет иметь четыре неопределенных константы, так как имеются два дифференциальных уравнения второго порядка, которые полностью нельзя определить из двух граничных условий (7). Для однозначного решения задачи предположим, что вторыми производными можно пренебречь ( S = 0). Тогда вместо системы (6) запишем:

a S i +n S i =YS 0 ■ aS 0 =7* S i

С учетом граничных условий (7) решение системы (8) имеет вид:

S 1 ( z ‘ ) =

2 / - ⁿ     Dz'

—e ^{2 a} sh|---

2 a

S 0 ( z ') =

D

- V Г f Dz') n J Dz') e 2a chl----I + — shl----I ,

I 2a J D I 2a J

где

D = n ² + 4 |Y ² .

Параметр n - есть расстройка Брегга. При П =0 решение (9) упрощается:

S1(z ') = shf ^-I

I a J

S0 (z ‘) = chf ^-1

I a J или в исходных обозначениях:

^S i ^{( z} ) = i sin

S ₀ ( z ) = cos

n(£1 - £3 )C1 z

X£ 0 - £ 1 sin² 9

n ( £ 1 - £ 3 ) C 1 z

^£ 0 - £ 1 sin² 9

Из решений (11) видно, что суммарная энергия обоих порядков при распространении в зоне модуляции рельефа решетки сохраняется ( S 1 ² ( z ) + S ₀ ² ( z ) = 1, 0 <  z <  d ).

Световая энергия «перекачивается» по мере проникновения излучения вглубь решетки из нулевого порядка в первый и обратно.

На рис. 2 показаны зависимости дифракционной эффективности нулевого порядка от глубины решетки (z/ X = d / X ), рассчитанных в разных приближениях: на основе решения системы уравнений (6) с сохранением вторых производных (кривая из темных квадратов); на основе решения двухволнового приближения с решением (11) (кривая из светлых квадратов); на основе численного решения исходной системы уравнений (4) при сохранении 2-х отраженных и 4-х прошедших порядков дифракции (кривая из треугольников). Расчет проводился для бинарной решетки с одной ступенькой рельефа на периоде и при следующих параметрах:

T a = , £ = 1, £ = 2.5, X = 0.63 мкм, 21          3

9 = 30o, X = 1, £ = £1+£3, m = 1, C = -.

T ⁰     2               ¹ n

Второе уравнение в системе (11) предсказывает значение первого минимума кривых на рис. 2. Из условия

n(£1 - £3 )C1 d _ П

X£o - £1 sin2 9  2

при выбранных параметрах получаем — « 1.39 . X

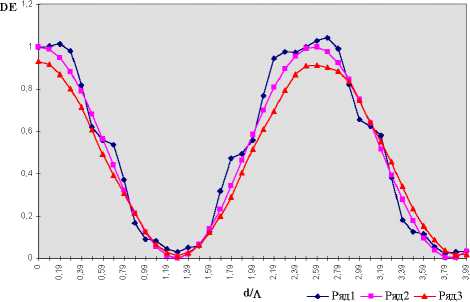
Рис.2. Зависимость дифракционной эффективности 0-ого порядка (рассчитанной в разных приближениях) от глубины бороздки решетки (бинарная решетка).