На протяжении более 40 лет научный коллектив, возглавляемый С.Э. Шнолем, проводил исследования закономерностей различных физических, химических и биологических процессов [1]. Было обнаружено, что радиоактивный распад – это процесс, который подчиняется статистике Пуассона, но гистограмма распределения имеет тонкую структуру – множественные пики и впадины (полиэкстремальность). Аналогичные результаты были получены при изучении закономерностей химических реакций и биологических процессов. Более того, авторы исследования доказали, что форма тонкой структуры процессов разной природы подвержена периодическим изменениям с периодами 24 ч, около 27 суток и 365 суток, однако этим фактам не было дано никаких объяснений и не было выдвинуто никаких гипотез о возможных механизмах возникновения этих явлений. На основании этих результатов можно сделать предположение о существовании неизвестной космофизической причины, которая влияет на случайные процессы различной природы. Эта публикация вызвала дискуссию в научных кругах. В частности, Е.А. Кушниренко и И.Б. Погожев дали критические замечания к статье С.Э. Шноля [2]. В своих комментариях авторы предположили, что в работе не хватает оценок статистической значимости, которые помогают отделить твёрдо установленные научные факты от правдоподобных предположений и научных гипотез.

На протяжении 10 лет А.В. Каравайкин работал над созданием устройства, которое способно повлиять на процесс радиоактивного распада [3]. По его утверждению, ему удалось создать прибор «НГК-ВЕГА» – генератор неэлектромагнитной информации. А.В. Каравайкин совместно с А.Г. Пархомовым провели измерения влияния излучения этого генератора на процесс радиоактивного распада препарата Co60 [4]. Оказалось, что такое воздействие никак не сказалось на средней активности препарата, но значительно уменьшило разброс результатов измерений. Это дало основание авторам исследования утверждать о возможности управления хаотическими явлениями, такими, как радиоактивный распад. Эти выводы столь фундаментальны и совершенно изменяют устоявшиеся представления о закономерностях хорошо изученных ранее физических явлений, что нуждаются в тщательной проверке независимыми исследователями.

Измерения гамма-фона

В настоящей статье представлены результаты исследования гамма-фона. Измерения проводились в одной из лабораторий Южно-Уральского государственного университета в круглосуточном режиме на протяжении 7 суток. Счётчик Гейгера с трубкой СБМ-20 был соединён с компьютером. Никаких источников радиоактивного излучения вблизи трубки Гейгера не было. Счёт производился непрерывно, но результаты измерений записывались с периодом 32,8 с. Всего было зафиксировано N = 16 300 временных интервалов. Помимо текущего времени, в файл записывались следующие данные за каждый период j (j = 1, …, N): Nj – число всплесков, Rj – средний вре- менной интервал между всплесками и VRj – коэффициент вариации временных интервалов между всплесками (среднеквадратичное отклонение, делённое на среднюю величину - GRj /Rj ). Число всплесков за определённый период должно иметь распределение Пуассона, а интервалы между всплесками – экспоненциальное распределение. Согласно [5], коэффициент вариации VRj экспоненциального распределения равен 1, а для пуассоновского процесса коэффициент вариации VNj = У^Nj^. Гистограмма количества скачков N в течение выбранного интервала времени имела вид пуассоновского распределения. Никакой тонкой структуры, а тем более полиэкстремальности, гистограммы не отмечено. В дополнение к этому, было произведено моделирование процесса. При моделировании процесса учитывалось, что трубка Гейгера после всплеска в течение 0,2 с не регистрировала частицы (время латентности). Поэтому процесс не являлся чисто пуассоновским. Полагалось, что усреднённый по N измерениям средний временной интервал между всплесками, полученный в эксперименте ( = 2,17 c), такой же, как и при моделировании. В то же время, усреднённый по N измерениям коэффициент вариации случайной величины Rj по экспериментальным данным оказался равным = 0,89, а при моделировании = 0,81. Это указывает на то, что при моделировании не были учтены какие-то факторы. На это же указывает некоторое отличие в ширине гистограмм (VNj = 0,228, 1J^Nj^ = 0,248).

Неожиданные результаты были получены при построении функции плотности вероятности нормированного среднего интервала между всплесками Rjj =(Rj -M (Rj))/or (рис. 1). Оказа лось, что f (Rij) не является гауссовой кривой, как можно было ожидать, а имеет тонкую структуру, в которой проявляется полиэкстремальность. Столь же интересные результаты были получены при построении функции плотности вероятности от двух переменных – Rɶj и Vj =( Vj - M (Vj))^VV (рис. 2). Количество временных интервалов при моделировании варьировалось от 20 млн. до 200 млн. Это не повлияло на график существенно. Дополнительно было проведено моделирование процесса при условии, что время латентности трубки СБМ-20 равно нулю. Это лишь немного изменило форму изолиний, но тонкая структура осталась подобной.

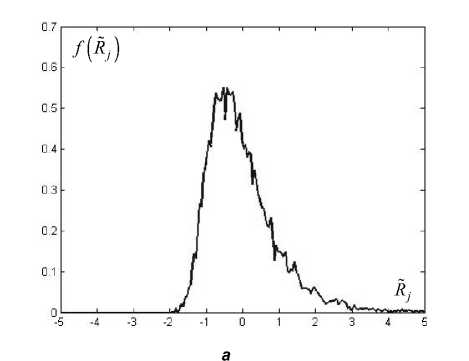
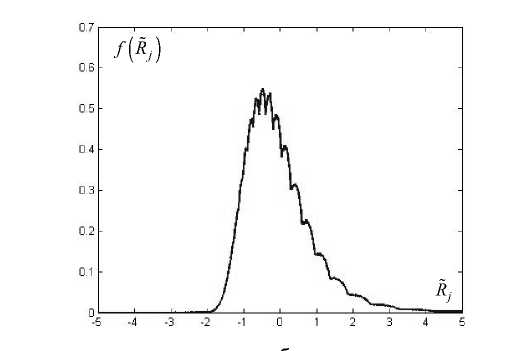
Рис 1. Функция плотности вероятности f ( R j ) , полученная по экспериментальным данным ( а ) и путём моделирования ( б )

Выводы

• 1)    Обнаружена полиэкстремальность функции распределения гамма-фона.

• 2)    Тонкая структура распределения случайных величин, например, среднего временного интервала между всплесками тока в трубке Гейгера может проявиться по естественным причинам, даже если не предполагать влияние космофизических условий.

  Физика

  
  
  
  
  
  
  
  

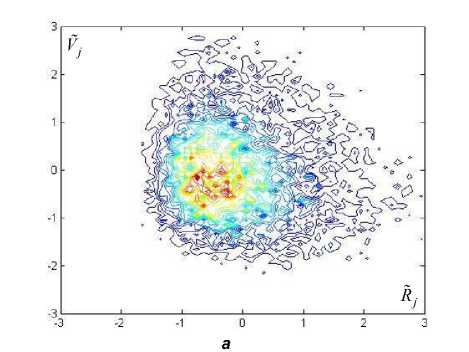
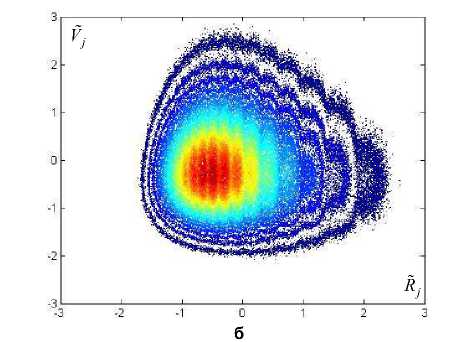
Рис 2. Изолинии функции плотности вероятности f ( R j , V j ) , полученные по экспериментальным данным ( а ) и путём моделирования ( б )