Двумерный алгоритм половинного деления и метод пристрелки при линейном анализе устойчивости равновесия конвективных процессов

Исследование любой физической задачи в идеальной ситуации включает в себя разные методы: теоретический, экспериментальный, численное моделирование. Созданные при этом подходы и методики часто дополняют друг друга, позволяют проверять полученные результаты, полно объяснять изучаемые явления, прогнозировать поведение физических систем в области параметров за пределами их известных значений и другое.

Отправной точкой многих теоретических способов является рассмотрение некоторой линеаризованной системы уравнений, описывающей поведение физической системы. Затем проводится линейный анализ устойчивости ее решения. Так, например, динамика жидкости и газа в системе, в том числе неизотермической, а также с учетом переноса вещества [1, 2], эффекта термодиффузии [3–5], динамика электропроводящей среды [6], систем в поле вибрационных сил [7], неньютоновских жидкостей [8] и другого представляются в виде системы нелинейных уравнений Навье–Стокса.

В практическом отношении линейный анализ устойчивости зачастую сводится к нахождению некоторых критических чисел задачи, то есть особых величин параметров (преимущественно безразмерных), при которых происходит качественное изменение поведения системы. С такой ситуацией можно

встретиться, например, при рассмотрении подогреваемой снизу жидкости в поле силы тяжести: при небольших значениях числа Релея Ra , отвечающего за интенсивность нагрева, наблюдается состояние механического равновесия, однако при достижении числом Ra некоторого критического значения возникает конвективное течение. Можно отметить классические результаты исследования возникновения конвекции в областях с твердыми границами, обладающими высокой теплопроводностью, согласно которым имеют место следующие пороги: Ra = 1708 для плоского слоя; Ra = 5100 для кубической области с изотермическими боковыми границами; Ra = 2500 для кубической области с адиабатическими боковыми границами [1, 9]. Возможна также ситуация, при которой основное состояние не является механическим равновесием, данное состояние системы может потерять устойчивость при достижении некоторых критических значений управляющих параметров. Например, в вертикальном плоском канале с поперечным нагревом реализуется течение с кубическим профилем скорости [2], которое теряет свою устойчивость при числе Грасгофа Gr = 495 (в пределе малых чисел Прандтля). Безусловно, задачи поиска различных параметров устойчивости встречаются не только при исследовании конвективных процессов. Так, известна проблема потери устойчивости плоскопараллельного течения (задача Орра–Зоммерфельда) [10]. Потеря устойчивости течением Пуазейля характеризуется переходом от параболического профиля скорости к более сложному.

При всем этом необходимо сделать важную оговорку: исследование устойчивости выполняется при возмущениях лишь определенного вида; в текущей работе рассматриваются только плоские нормальные возмущения экспоненциального вида: ~ exp ( -X t ) , где X — декремент возмущений (устойчивость системы определяется знаком его действительной части — X R , а пороги устойчивости при этом соответствуют области параметров, в которой X R = 0). Таким образом, с математической точки зрения имеется краевая задача для дифференциальных уравнений, из решения которой находятся собственные числа X . Необходимость в решении задач подобного рода встречается во множестве физических приложений: от простых колебаний (рассматривается уравнение гармонических колебаний) до квантово-механических явлений [11] (решаются уравнения Шрёдингера, Хартри–Фока и другие). Исходя из того, что необходимо решать и зачем, логичным является следующий вопрос: «Каким образом это сделать?». В некоторых частных случаях можно получить аналитическое решение, попытавшись угадать собственные функции задачи. Например, в задаче конвекции плоского подогреваемого снизу слоя со свободными границами решение оказывается элементарным, в виде тригонометрических функций [1]. На практике, конечно, такие ситуации являются крайне редкими, и приходится прибегать к приближенным вычислительным алгоритмам. К ним можно отнести методы, хорошо зарекомендовавшие себя при решении задач гидродинамики: метод Галёркина, метод дифференциальной прогонки, метод пристрелки [2, 12]. В текущей работе будет использоваться последний из перечисленных, который, в отечественной литературе встречается и под другими названиями: метод пошагового интегрирования с ортогонализацией, метод построения фундаментальной системы уравнений (возможны и другие варианты; в англоязычной литературе это «shooting method»). Основная идея данного метода заключаются в следующем: решение краевой задачи сводится к задаче Коши для системы однородных дифференциальных уравнений, на последнем шаге алгоритма получается функция f ( X ) = 0 , в общем случае — в поле комплексных чисел, что эквивалентно двум действительным уравнениям. Таким образом, на последнем шаге требуется решить задачу поиска корней системы уравнений.

В одномерном случае, когда в системе отсутствует комплексная часть декремента, надежным и одновременно самым простым в реализации является метод половинного деления (также именуемый методом дихотомии; в англоязычной литературе — «bisection method»). В общем случае для систем уравнений, как правило, применяются такие методы, как метод секущих, метод Ньютона и другие. Обобщения метода половинного деления, безусловно, существуют [13–15]; среди них следует отметить часто используемый метод Нелдера–Мида [13], однако на практике он, как правило, не используется, что объясняется прежде всего тем, что другие методы оказываются существенно эффективнее (можно даже сказать, математически более изящными) и также относительно несложными в реализации. При этом классические учебники по численным методам про метод половинного деления применительно к системам уравнений зачастую ничего не пишут (см., например, [16, 17]), иногда даже можно встретить высказывания: «… на системы уравнений дихотомия не обобщается» [18].

Ранее обнаружено [19], что при решении линейной задачи устойчивости трехкомпонентной жидкой смеси использование метода пристрелки в комбинации с методом секущих может приводить к значительным трудностям при нахождении критических чисел в силу необходимости задания начального приближения, близкого к искомому решению. Для преодоления этого далее предлагается одна из возможных реализаций метода половинного деления для случая двух переменных; на примере рассмотренной ранее задачи [19] показана его высокая эффективность при исследовании конвективных процессов, сопровождающих тепло-и массообмен.

2.    Конвекция трехкомпонентной смеси с эффектом Соре (1,0 z dT к--= -q g (0,0) f az x Рис. 1. Геометрия задачи

Рассмотрим задачу устойчивости механического равновесия трехкомпонентной смеси в плоском горизонтальном слое при подогреве сверху и снизу в поле силы тяжести с заданным тепловым потоком на верхней и нижней твердых непроницаемых для вещества границах (Рис. 1).

Уравнения свободной конвекции в приближении Буссинеска для n -компонентной несжимаемой жидкости имеют следующий вид [3]:

— + v-Vv = -—Vp + vV2 v-(PTT + IBC) g,(1)

5tP div v = 0 ,(2)

^T + v-V T = %V2 T,(3)

о t ac

— + v-VC = DV2C + DV T .(4)

a t

Здесь: v = ( v x , v y , v z ) — вектор скорости в декартовой системе координат c радиус-вектором r = ( x , y , z ) ; C = (Q, C ₂. . C n , ) T — транспонированный вектор компонентов концентрации; T — температура (значения температуры и концентрации будем отсчитывать от некоторых средних значений T ₀ и C ₀ ); p — давление; g = ( 0,0, - g ) — вектор ускорения свободного падения; р ₀ — средняя плотность; v — кинематическая вязкость; х — коэффициент температуропроводности; D _T = ( D_T 1 , D_{T 2} . D n 1 ) T — вектор коэффициентов термодиффузии; D — квадратная матрица коэффициентов диффузии c компонентами D i. ( i , j = 1,., n -1 ) ;

P T =

1 dp

P 0 d T

— коэффициент теплового расширения; B = diag ( P _C 1 , P _C 1 . P _Cn - 1 ) — диагональная матрица,

C

где

P C =

1 dp . — — Po dCi

— коэффициенты концентрационного расширения;

I = ( 1,1,.,1) — единичный

T , C k , i * k

n - 1

вектор размерности n - 1 (таким образом IBC = ^ P _C C i ).

i

Для перехода к безразмерным параметрам выберем в качестве единиц измерения: для длины — вертикальный размер области h ; для времени — h2/v ; для скорости — v/h; для температуры — 0 ; для концентрации — PT0B для давления — pov2 /h2 ; для плотности — p0PT0. Введем малые возмущения: v = vb + v', p = pb + p', T = Tb + T', C = Cb + C', и будем рассматривать плоские нормальные возмущения вида:

v z ( x , z , t ) = w ( z ) exp ( -X t + i ( k x x + k y y T ' ( x , z , t ) = 9 ( z ) exp ( -X t + i ( k x x + k y y C ' ( x , z , t ) = c ( z ) exp ( -X t + i ( k x x + k y y

Здесь: X = X R + i to — комплексный декремент возмущений, где to — частота возмущений (при X R >  0 возмущения со временем нарастают); k_x , k _y — волновые числа. После линеаризации и исключения давления и продольных компонент скорости путем применения операции rot _z rot к уравнению (1) система (1)–(4) принимает следующий вид:

Ra

XAw + A2w-k2 ((1 + ^)9 + If ) = 0,

X0 + w + — AT = 0,(6)

Pr

X( f + y0) + V W + SCAT = 0.(7)

Систему уравнений (5)–(7) дополним следующими граничными условиями:

z = 0,1: u = du/dz = d 0/ dz = df/dz = 0.(8)

При записи уравнений (5)-(8) введены следующие обозначения и безразмерные параметры: f = c - у 0 — вспомогательная функция (для удобства записи граничных условий); к ² = к^ + к2 ; оператор A = d²/ dz ² - к^г (A² = d⁴/dz ⁴ - 2 к ■ d ²/ dz ² + к ⁴); число Релея Ra = g в _T 0 h ³ /(vx), где 0 = qh ³ /к ( q — удельный тепловой поток, к — коэффициент теплопроводности); число Прандтля Pr = v/x ; вектор отношений разделения V = ( у 1 , V ₂ ,^, V n - 1 ) = -в - ¹ BD ^{- 1} D T , где V i =-вгв Ci S Ti     ( S_Ti     — коэффициенты Соре);

n - 1

У у i = Т — суммарное отношение разделения; SC = v^{- 1} BDB ^{- 1} — модифицированная матрица чисел

Шмидта; SC jj = р Ci Др C _ySc -¹ ) , где Sc ij = v/ D ij — матрица чисел Шмидта, i , j = 1,..., n - 1. В работе объектом исследования является трехкомпонентная система, n = 3 .

В качестве примера рассмотрим некоторую характерную модельную жидкую смесь с параметрами: Pr = 10, Sc 1 = 100, Sc₂ = 1000, у 1 = 0.2 , у ₂ = - 0.4 и волновым числом к = 2 . Выбор примера обусловлен тем, что при данных параметрах в системе есть неустойчивость как при подогреве снизу (Ra >  0), так и сверху (Ra <  0), а в спектре возмущений имеются как колебательные ( ю ^ 0 ), так и монотонные ( ю = 0) моды.

• 3.    Задача поиска собственных чисел методом пристрелки

Детальное описание метода пристрелки можно найти в [2, 12]. Здесь же изложим только основные идеи. Краевая задача (5)–(8) включает: уравнение движения 4-го порядка, уравнение теплопроводности 2-го порядка, два уравнения диффузии 2-го порядка, что, как известно [12], можно свести к системе 10-ти уравнений 1-го порядка. При этом имеется 5 граничных условий при z = 0 , и столько же при z = 1. Согласно методу, краевая задача представляется как задача Коши, то есть нужно построить 5 линейно-независимых решений, на основе которых и находить общее решение системы из 5 уравнений. Для получения нетривиального решения необходимо, чтобы определитель этой системы был нулевым: D = 0 . Суть метода пристрелки заключается в том, что берутся пробные значения X до тех пор, пока определитель не будет равняться нулю; безусловно, это делается не вслепую, не до момента, пока наконец-то повезет. Определитель D можно рассматривать как функцию декремента возмущений и таким образом от исходной задачи перейти к поиску корней уравнения D ( X ) = D ( X R , ю ) = 0. В общем случае определитель D является комплексной величиной (когда ю ^ 0) и, кроме того, зависит как от управляющих безразмерных параметров системы уравнений (5)–(7), так и от волнового числа k . Однако, как управляющие безразмерные параметры, так и волновое число можно зафиксировать и решать систему 2-х уравнений с 2-мя неизвестными. А поскольку интерес представляет порог возникновения конвекции, задачу удобнее переформулировать: считать неизвестной величиной, наравне с ю , число Релея Ra , положив:

X R = 0     D r ( Ra,ю ) = 0,                                       (9)

D m ( Ra, ю ) = 0.                                        (10)

Для решения системы уравнений (10) ранее (см. [19]) использовался метод секущих. В качестве начального приближения на плоскости (Ra, ю) задавался некоторый треугольник с координатами вершин: Таблица 1. Критические числа X при Pr = 10 , Sc, = 100 , Ra1, ю1; Ra2, ю2; Ra3, ю3. Находилось новое приближение Ra4, ю4. После Sc2 = 1000 , У| = 0.2, этого одна из старых точек треугольника отбрасывалась, и процедура повторялась до тех пор, пока решение не сходилось в точку (с заданной точностью). Исходя из прошлого опыта, ограничимся отрезком по оси V = -0.4, к = 2 X Ra ю Ra от –2000 до +2000. В данном диапазоне существуют 4 корня, № 1 50.4 0 перечисленные в таблице 1. Метод секущих хорошо работает в большом числе случаев и требует при этом проведения небольшого объема вычислительных действий. Однако при поиске корней уравнений в задаче с колебательной неустойчивостью № 2 1374.5 0 № 3 1461.0 0.174 № 4 –1809.1 0.046 данный метод оказался трудно применимым. В таблице 2 представлены результаты вычислений в зависимости от начального приближения при попытке найти корень № 3 из таблицы 1 (две других начальных точки отстояли от Ra3, «3 на 10%; образуемый при этом треугольник был равносторонним). Положительный результат достигался только в том случае, если начальное приближение (в особенности по частоте о) оказывалось близким к искомому корню, но даже это не всегда гарантировало успех вычислений.

Таблица 2. Результаты поиска корней X в зависимости от начального приближения (символ х означает, что решение разошлось)

Ra	1400	1300	1200	1500	2000	1500	1300	1200	1600	2000	1461	1400	1400	1400	1000	100	–1000	–1800	1461	1461	1461	1461	1461
ю	0.10	0.10	0.10	0.10	0.10	0.01	0.01	0.01	0.01	0.01	0.17	0.17	0.18	0.15	0.17	0.17	0.17	0.17	0.10	0.25	0.19	–0.17	1.00
Номер X	3	4	2	×	4	2	2	2	2	×	3	3	3	1	3	3	3	3	4	2	3	3	×

Например, при начальном приближении (1500, 0.10) итерационный процесс нахождения решения разошелся, при (1400, 0.15) он сошелся к корню для монотонной неустойчивости (50.4, 0). Исходя из этого, можно заключить, что существует риск пропустить некоторые корни и получить неполное решение задачи. В более ранней работе [19] преодолеть данную трудность удалость лишь путем тщательного подбора начального приближения (это потребовало большого количества времени), а также при помощи длинноволнового анализа, благодаря которому были найдены пороги длинноволновой неустойчивости. Отметим, что корректность решения подтверждается согласием результатов c результатами нелинейных расчетов [20], а в предельных случаях —с данными длинноволнового анализа [19].

4.    Двумерный метод половинного деления, реализованный с помощью квадро-дерева

Реализация программы поиска критических чисел задачи показала, что первый этап алгоритма — этап, на котором осуществляется численное интегрирование задачи Коши с целью получения определителя D , работает эффективно. Следовательно, для того чтобы преодолеть трудности, связанные с заданием начального приближения и улучшить методику поиска параметров устойчивости (то есть корней системы уравнений (9), (10)), была предпринята попытка скорректировать процедуру.

С геометрической точки зрения решение системы уравнений (9), (10) представляет собой точки взаимного пересечения функций D R , D Im с плоскостью D = 0. Иначе говоря, необходимо найти такие точки, где D_R и D_Im одновременно меняют знак. На первом шаге произвольно выбираем некоторый прямоугольник ABCD на плоскости ( Ra, to ) и проверяем знаки у функции D R в его вершинах. Если знаки не совпадают, осуществляем такую же проверку для D_Im . При одинаковых знаках производим деление прямоугольника на 4 равные части и проверяем в каждой из них знаки в вершинах. Выполняем деление прямоугольников до тех пор, пока их линейные размеры не станут меньше некоторого заданного с . На рисунке 2 схематически представлены 3 первых шага выполнения алгоритма.

Отметим, что многие классические реализации обобщенного метода половинного деления [13–15], в виду большей эффективности, предлагают применять n -мерный симплекс (треугольник на плоскости), а не n -мерный параллелепипед (прямоугольник на плоскости). Однако, в данной работе принимаем, что при небольших линейных размерах разница в эффективности является незначительной и, в силу простоты реализации, отдаем предпочтение прямоугольнику. Это позволяет при программировании алгоритма воспользоваться квадро-деревом (quad tree) — структурой данных, у которой имеется 4 потомка того же типа, что и родительский элемент. На языке программирования C/C++ это легко реализуется с помощью процедуры, включающей: создание массива координат центров ячеек — (Ra, to ) , формирование 4-х указателей того же типа (при делении пространства для них выделяется память), сообщение каждому потомку координат ячейки. Затем процедура повторяется.

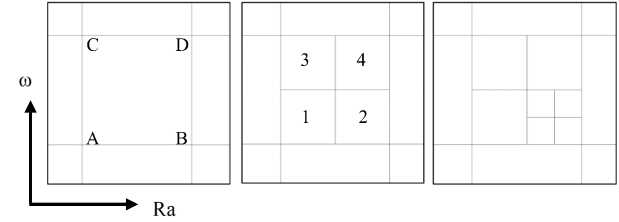
Рис. 2. Выполнение метода половинного деления на плоскости

На рисунке 3 графически представлены результаты выполнения созданной авторами программы поиска критических чисел задачи конвекции при вертикальном нагреве на основе метода пристрелки и двумерного аналога метода половинного деления. Общая площадь поиска соответствовала области - 2000 <  Ra <  2000, 0 < го <  0.2 с ее начальным делением на 16x16 прямоугольников (для удобства деление представлено в виде квадратов).

Остановимся на следующих важных вопросах.

Если в одномерном случае — на отрезке — функция меняет знак, значит в соответствующем интервале присутствует, как минимум, один корень. Для плоскости аналогичное высказывание не является справедливым. Если рассматривать прямоугольник ABCD (Рис. 2), условие поиска может быть удовлетворено уже на первом шаге, то есть функции D_R и D_Im одновременно меняют свой знак в узлах, однако затем, при более мелком дроблении области, может оказаться, что внутри прямоугольника ABCD они меняют знак не в одной точке пространства (так, например, D_R меняет знак в прямоугольнике 3, а D_Im — в прямоугольнике 2). Таким образом, происходит ложное срабатывание алгоритма, и корни системы уравнений в данной области в действительности отсутствуют. На рисунке 3 можно видеть множество подобных «ложных» срабатываний (некоторые квадраты делятся 1–3 раза). При реализации выбиралась точность е = 10 ^{- 6}, для достижения которой производилось 29-кратное деление пространства, при этом «ложное» деление в одном прямоугольнике происходило не более 4-х раз.

Другим интересующим вопросом является быстрота и эффективность работы алгоритма. Метод секущих и метод половинного деления сильно отличаются друг от друга, что затрудняет их сравнение. При точности е = 10 ^{- 6} в случае монотонной неустойчивости ( го = 0) метод секущих позволяет найти решение в среднем за 5–10 итераций, при колебательной неустойчивости — за 10–20 итераций: при хорошем начальном приближении число итераций приблизительно в 2 раза меньше.. При этом на каждой итерации методу секущих отвечает больший объем арифметических действий, в том числе расчеты по формулам координат пересечения плоскостей с вычислением определителей и прочее. Для нахождения всех корней (при параметрах, перечисленных выше) методу половинного деления необходимо 29 итераций.

Однако, независимо от того, какой из двух методов используется, время выполнения алгоритма измеряется секундами или долями секунд, то есть скорость работы программы на практике не представляет никакой сложности (в отличие от прямого численного моделирования уравнений Навье–Стокса и других задач). Последнее утверждение, впрочем, справедливо лишь при условии адекватного деления на части исходной области поиска на плоскости ( Ra, го ) . На рисунке 4 представлена зависимость времени выполнения алгоритма от m — начального числа делений по одному направлению (то есть всего рассматривается m х m прямоугольников). Время работы программы ожидаемо квадратичным образом растет с увеличением m , и при чрезмерном начальном дроблении области скорость поиска критических чисел существенно замедляется. С другой стороны, при достаточно грубой настройке повышается риск пропустить определение некоторых X; так, обнаружено, что при m <  15 алгоритм не находит корень № 4 (самый левый на рисунке 4, при отрицательных значениях Ra ), остальные корни устанавливаются при любом m >  1.

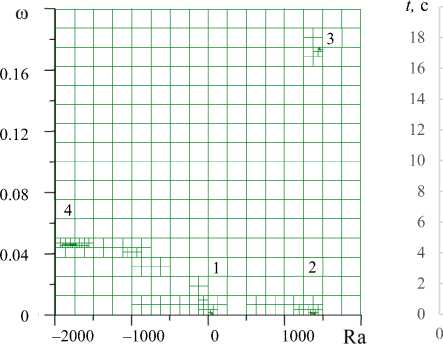
Рис. 3. Графическое представление реализации программы поиска критических чисел с помощью метода пристрелки и двумерного аналога метода половинного деления; цифрами обозначены номера корней из таблицы 1

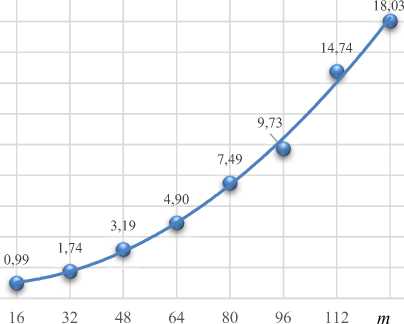
Рис. 4. Зависимость времени счета по программе, измеряемого в секундах, от параметра m (начального числа делений пространства поиска корней уравнений)

5.    Заключение

Представлена модификация метода пристрелки для нахождения критических чисел в задачах с конвекцией, возникающей в процессах тепло- и массообмена. Претворена идея использования на последнем шаге алгоритма обобщенного метода половинного деления. Метод половинного деления в большинстве случаев, особенно в задачах, сводящихся к системам уравнений, уступает методу секущих, методу Ньютона и другим. Однако, как показано в данной работе, при решении реальных физических задач именно метод половинного деления может справиться с трудностями, которые возникают в других подходах. В заключение отметим, что несколько разных методов всегда могут служить для проверки друг друга и таким образом повышать достоверность полученных результатов и качество исследований.