Dynamic Load Balancing using Graphics Processors

Published Online April 2014 in MECS

Today’s graphic processors have ventured from the multicore to the many-core domain; with many problems in the graphics being of the so called embarrassingly parallel kind; [1, 2] there is no question that the number of processing units will continue to increase.

GPU can handle a great amount of data parallel applications with its massive parallel processing functionality. Many applications are highly suitable for GPU computation, the most effective of them being Interactive visualization. With the possibility of simultaneous execution of multiple tasks on different GPU'S, and the ability to perform computations that overlap; multiple GPU'S can easily increase the efficiency of these applications. This opens the window for processing large scale problems in contrast to a single GPU model that cannot handle these problems in real time.

Popular GPU computing environments like CUDA and OpenCL ease the uphill problems of scheduling jobs whose computation costs are unknown by achieving load balancing. Load balancing is established by decomposing the main job into subtasks which can be executed concurrently by assigning fresh unfinished tasks to cores that finish early. However load balancing requires all tasks to be available before the kernel is called. Subtasks created during runtime wait for the kernel as a whole to finish and then get executed in a new kernel invocation. Subtasks are also executed by making each core perform all of its own subtasks.

To be able to take advantage of this parallelism in general purpose computing, it is imperative that the problem to be solved can be divided into sufficiently fine-grained tasks to allow the performance to scale [3] when new processors arrive with more processing units. However, the more fine-grained a task set gets, the higher the cost of the required synchronization becomes. Several popular load balancing schemes have been hard to implement efficiently on graphics processors due to lack of hardware support, but this has changed with the advent of scatter operations and atomic hardware primitives such as Compare-And-Swap. It is now possible to design more advanced concurrent data structures and bring some of the more elaborate dynamic load balancing schemes from the conventional SMP systems domain to the graphics processor domain. The load balancing in these schemes is achieved by having a shared data object that stores all tasks created before and under execution. When a processing unit has finished its work it can get a new task from the shared data object. As long as the tasks are sufficiently fine-grained the work load will be balanced between processing units.

Synchronization of the memory access to the shared data can be achieved either through blocking or nonblocking. Blocking methods employ the usage of locks to grant permission to only one processing unit to access the object. As is evident, the method assumes conflicts to exist even when there are no conflicts. Non-blocking methods on the other hand, makes several processing units to simultaneously access the shared data object only when a conflict arises. It takes a more hands on approach for conflict resolution. Delays occurs only when there is an actual conflict This feature allows      better with increase in number of processing units.

algorithms using non-blocking methods to perform

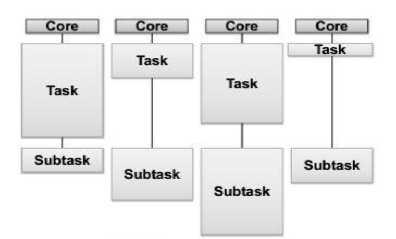
Fig. 1: Diagrammatic Representation of Static Task Assignment (left) and Dynamic Task Assignment

The paper compares two different methods of dynamic load balancing:

• •    Static Task List: Tasks are stored in a static list [4].

• •    Task Stealing: Each processing unit has a local double ended queue where it stores new tasks. Tasks can be stolen from other processing units if required [5].

• II.    Load Balancing Methods

• 2.1    Static Assignment

This section gives an overview of the two different load balancing methods we have compared in this paper.

The default method for load balancing used in CUDA is to divide the data that is to be processed into a list of blocks or tasks. Each processing unit then takes out one task from the list and executes it. When the list is empty all processing units stop and control is returned to the CPU. This is a lock-free method and it is excellent when the work can be easily divided into chunks of similar processing time, but it needs to be improved upon when this information is not known beforehand. Any new tasks that are created during execution will have to wait until all the statically as-signed tasks are done, or be processed by the thread block that created them, which could lead to an unbalanced work-load on the multiprocessors.

To evaluate the performance of the work-stealing scheme, a load balancing scheme using a static assignment of the tasks to each thread block was implemented [6]. Thread blocks were considered instead of threads because for some applications, (e.g., where control flow across tasks can diverge heavily) it would be more efficient to have multiple threads within a block collaborate on a single task rather than to have each thread work on its own task.

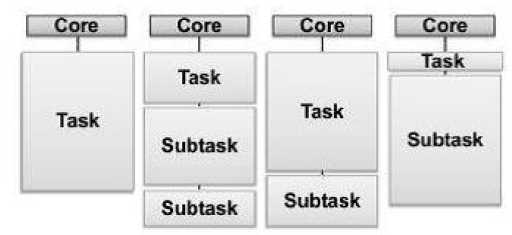
The work-pool in this scheme is implemented using two arrays (Fig. 2). The first array holds all the tasks to be performed, and the other array holds the subtasks created at runtime. In the first iteration, the input array holds all initial tasks. The array is then partitioned so that each thread block gets an equal number of tasks. Since no writing is allowed to the input array, there is no need for any synchronization.

When new tasks are created during runtime, they are written to the output array with the help of the atomic primitive Fetch-And-Add (FAA). This primitive atomically increments the value of a variable and can thus be used to find a unique position in the array. When all tasks have been completed, the two arrays switch roles and the kernel is invoked again. This is repeated until no more new tasks are created.

Pass N (in)

Pass /V+1 (out)

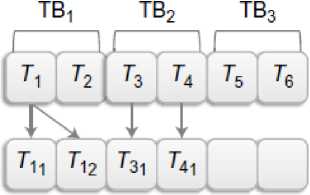
Fig. 2: Static assignment using two arrays

A pseudocode for Static Task List [7] is, function DEQUEUE(q,id)

return q.in [ id ]

function ENQUEUE( q,task )

localtail ← atomicAdd ( &q.tail ,1)

q.out[localtail] = task function NEWTASKCNT(q)

q.in,q.out,oldtail,q.tail ← q.out,q.in,q.tail ,0

return oldtail procedure MAIN(taskinit)

q.in,q.out ← newarray ( maxsize ), newarray ( maxsize )

q.tail ← 0

enqueue ( q,task init )

blockcnt ← newtaskcnt ( q )

while blockcnt ≠ 0 do run blockcnt blocks in parallel

• t ← dequeue ( q,TB_id )

subtasks ← doWork(t) for each nt in subtasks do enqueue(q,nt)

blocks ← newtaskscnt ( q )

Additionally, the pseudocode for Blocking Based

Dynamic Queue [7] is, function DEQUEUE(q)

while atomicCAS(&q.lock ,0,1) == 1 do

If q.beg! = q.end then q.beg++ result ← q.data[q.beg]

else result ← NIL q.lock ← 0

return result function ENQUEUE(q,task)

q.data[q.end] ← task q.lock ← 0

• 2.2    Work-Stealing

Static assignment as a solution to load balancing scheme has not found traction. A more popular approach is Task Stealing. The basic principle is that a processor which is allotted a set of tasks, once it has completed them tries to “steal” a task from another processor which is yet to complete the assignment done. If the processor manages to steal as task, a new task is created and added to its own set of tasks.

As already illustrated, a thread block is allocated a work-pool for it to work with. This work-pool can initially contain some pre-allocated tasks to begin with. When a new task is created at run time, the task is added to the work-pool. If a particular thread block is not allotted a task, it checks to see if all the tasks assigned to the system are completed. If the check fails, task stealing is done by that particular thread block.

The modeling that we have used to achieve work stealing finds its application in several traditional systems. The main aspects of the modeling are two features: Lock-free and avoid atomic operations.

As is evident from the design of the task-stealing algorithm, multiple blocks have access to the same work-pool. To support this feature, the implementation of the work-pool should be able to manage and synchronize the various actions operated on it by the blocks. To achieve this economically, lock-free techniques have been put to use. Lock-freedom is essentially an assurance that no deadlock occurs and at any particular time, progress is made on the tasks by at least one block independent of the situation at the other blocks. This assurance implies the fact that the delay burden on a block, for a lock to be released is zero.

The work-stealing algorithm uses double-ended queues (deques) for work-pools and each thread block is assigned its own unique deque. A deque is a queue where it is possible to enqueue and dequeue from both sides, in contrast to a normal queue where you enqueue on one side and dequeue on the other. Tasks are added and removed from the tail of the deque in a Last-In-First-Out (LIFO) manner [8].

When the deque is empty, the thread block tries to steal from the head of another thread block’s deque. Since only the owner of the deque is accessing the tail of the deque, there is no need for expensive synchronization when the deque contains more than one element. Several thread blocks might however try to steal at the same time, and for this case synchronization is required, but stealing is expected to occur less often than a normal local access.

We base our implementation on an array that holds the tasks, and have a head and a tail pointer that points to the first and last task in the deque. The head pointer is divided into two fields due to the ABA-problem which can occur if the head pointer is written to by two different thread blocks. The ABA problem is the situation where a value has changed its value from A to B and then back to A again without the system discovering the change in between.

As each thread block needs to have its own deque, we have to allocate memory for as many deques as we have thread blocks. We cannot use the shared memory to store the deques, as other thread blocks need to be able to access them to steal tasks. The maximum number of tasks to make room for in the deque will have to be decided for the specific application and must be decided on beforehand. The tasks can be of any size. If they are larger than a single word, one should try to make sure that multiple threads read them in a coalesced manner [11].

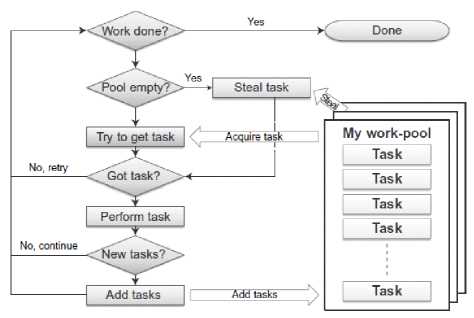
Fig. 3: Task Sharing using Work stealing and work pools

• III.    FOUR-IN-A-ROW

• 3.1    Design

Four-in-a-row game also known as Connect Four is a game involving two players. Each player chooses a colour and then takes turns dropping the respective coloured tokens into a seven column-six row grid. The objective of the game is to win by getting four of the same tokens in a row. The player achieving this is declared the winner. Several dimensions of the grid exists, here we restrict ourselves to a 6X7 grid. Fig. 3 shows a possible game beginning and follows up.

To help the computer pick the optimal move, n moves need to be looked ahead, and a min-max algorithm is used to pick the move that gives the best worst case scenario. In Figure 4 we see the decision tree used in the algorithm. The nodes at the first level represent one of possible moves that the player makes.

The children of these nodes represent the moves that the computer can take in the next turn, given the first move. The children of these nodes in turn represent the move that the user can make and so on, until we have looked n moves ahead.

When a leaf node is reached, either due to one of the players winning or because we have looked n moves ahead, a heuristic function e(p) is used to give each leaf node a value depending on how good that outcome is. The computer winning is infinitely positive and the player winning is infinitely negative.

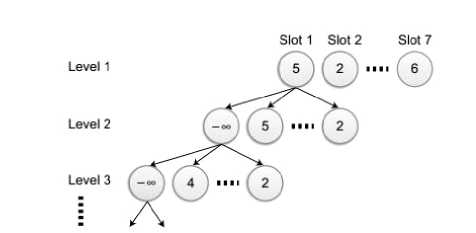
Fig. 4: A min-max decision tree for four-in-a-row. Each node is a task

The other scenarios are valued by the difference in how many two or three token sequences each of the players have. The nodes at even levels, which represent the computer player, take the value of the child node with the highest value, as this represents the computer’s optimal move. On the other hand, the nodes at odd levels which represent the human player, take the value of the child with the lowest value. In the end, the node on the first level with the lowest value represents the worst next move for the human opponent.

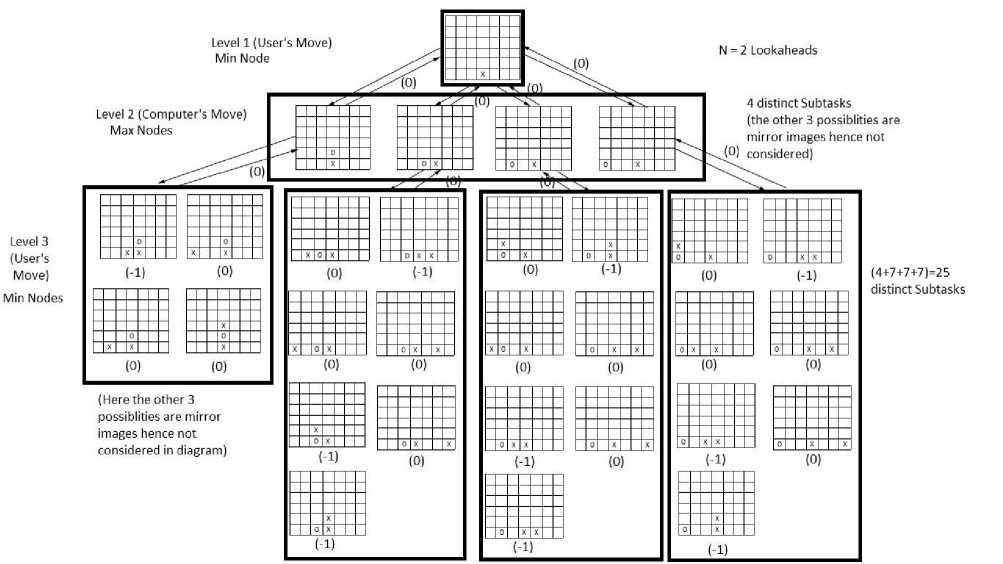
Fig. 5: The min-max tree showing the dynamic nature of tasks created developed for a particular user move with look ahead of 2 moves

It is hard to predict how much time will be spent in each branch. By making each node in the min-max decision tree a task, we can use dynamic load balancing to achieve an even load. We set each task to hold information on what level the node is on, its parent node, its value and the moves taken by its ancestor nodes. We save memory by only storing the moves taken and not the entire board state, as the new board state can be generated quickly from the current board state, and the moves can be taken. To know when the problem has been solved, we keep a counter at each node that keeps track of the number of child nodes it has received a value from. When the root nodes have received values from all of their children, the work is complete [9, 10].

e(P): static evaluation function for tip nodes

This is given by,

e(p) = (No. of 2 or 3 sequences for MAX nodes) – (No. of 2 or 3 sequences open for MIN nodes)

e(p) = ∞ if p is a win for MAX node

e(p) = -∞ if p is a win for MIN node

After calculating the e(p) values for the tip nodes we come back towards the root calculating the backed up values as follows:-

Backed up value for a MAX node = Maximum (e(p) values of all successor MIN nodes)

Backed up value for a MIN node = Minimum (e(p) values of all successor MAX nodes)

• IV.    Experimental Evaluation

The performance of the computer player is evaluated by playing the starting game scenario shown in Fig. 3 with different number of look ahead moves. Fig. 6 shows the numbers of tasks per millisecond performed by the two different load balancing schemes using 240 thread blocks. We see that the dynamic load balancing scales much better, when faced with a higher load, than the static load balancing. At 7 look ahead moves it is twice as fast as the static scheme [12].

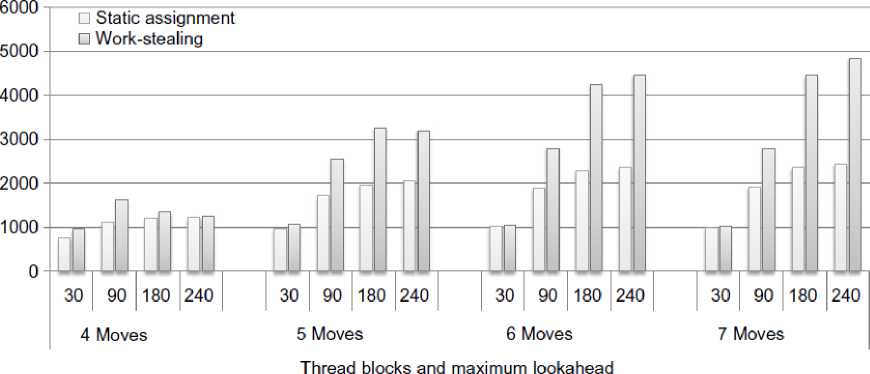
Fig. 6: Four-in-a-row: Tasks performed per millisecond for different number of look ahead moves and thread blocks

Fig. 7 also shows the number of tasks that needs to be allocated space. It is to be noted that, the scale is logarithmic. For the static load balancing, this is the maximum number of tasks that can be created in a kernel invocation. The dynamic load balancing has a deque for every thread block, so here the maximum number of elements needs to be multiplied with the number of thread blocks.

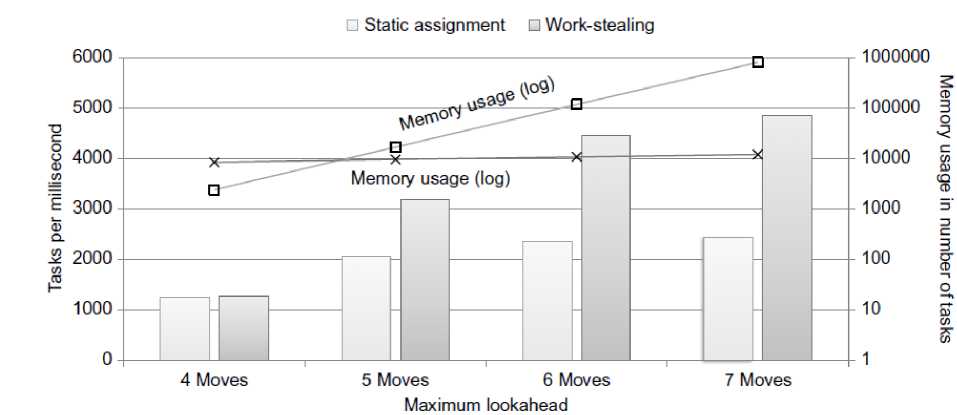
Fig. 7: Four-in-a-row: Tasks performed per millisecond and memory usage in number of tasks for 240 thread blocks

• V.    Conclusion

The two different load balancing schemes namely the ABP task stealing and static list were compared with each other by simulating a computer move for a human opponent in the classic game of four in a row game.

Since the number of tasks increased quickly, and the tree itself was relatively shallow the static queue performed well. The ABP task stealing method, however outperformed its static counterpart and produced better results for the said game.

For 7 look ahead moves, the static load balancing requires around 800,000 tasks to be stored, while the dynamic only requires 12, 000 tasks around 50 times the number of thread blocks.