Dynamic Programming and Genetic Algorithm for Business Processes Optimisation

Published Online December 2012 in MECS

• I.    Introduction

  Modern theories of organization and management assumes that organizations are built upon processes rather than existing or model structures and hierarchies. Tasks of organizations influence actions they take and functional organization structures they have. These tasks have their source in major goals like: sales, distribution, production, recruiting, marketing etc. Those tasks are performed as a part of so called business processes, which transforms input resources into deliverables. This management approach together with formal definitions and modelling has been around since beginning of 1990s.

Business process modelling techniques have been several times reviewed and classified i.e.: by Kettinger, Teng and Guha [1] in 1997, Melao and Pidd [2] in 2000 and Tiwari, Vergidis and Majeed [3] in 2008. Van der Aalst and Hofstede [4] have been analysing modelling techniques according to their ability to represent workflow patterns. Approaches reviewed by them enables visualization of processes and analysis of some of their characteristics like resource utilization, correctness of the structure, but does not provide significant support for process improvement. Neither review conducted by Cheung and Bal [5] have not presented formal optimization attempt of business process model.

Grigori et al. [6], Weijters and van der Aalst [7] recently proposed a process mining based on coming from Business Intelligence data mining tools for process discovery and analysis, but not for process improvement.

Hofacker and Vetschera [8], Zhou and Chen [9], Tiwari, Majeed and Vergidis [10] and several other authors have presented an algorithmic procedures for business process optimization based on formal mathematical model. Those researches in area of business process optimization deal with single-objective optimization (i.e. Hofacker and Vetschera [8]) or a selection of the business process model from the set of alternatives (i.e. Niedermann and Schwarz [11]).

The complex nature of business processes together with common existence of multiple objectives in commercial environments explains the hardship of preparing the mathematical model. There is a significant number of highly specialised algorithms for manufacturing processes (i.e. Ruml et al. [ 12]), but lack of business process improvement methods.

Other techniques have been also applied to formal mathematical and graph models of business processes basing on the structure rather than dynamic of the process. Sadiq and Orłowska [ 13], van der Aalst [14] have proposed graph reduction approaches to optimize process design. Heuristic rule of task reduction has been described in works of i.e. Rummel [15], Devan [16] or Wynn at al. [17].

Researchers prefer to focus on mathematical models, as they are not ambiguous and algorithmic approaches originating for operations research or task consolidation methods can be applied to optimise the process. Where diagrammatic model has its formal mathematical representation (i.e. Petri Nets) graph reduction techniques are used for optimisation purposes. Those techniques gives positive output but as even researchers themselves have spotted [3, 18], analysts are discouraged by the complexity of the method, work needed to prepare the mathematical model and complexity of understanding and explaining the results of optimisation.

That is why optimisation of business processes in the companies and organizations is done mostly manually, with some help of analysis. The optimisation procedure looks like this:

Step 1 Specify the system

Step 2 Identify the bottlenecks

Step 3 Choose among available modifications to resolve the performance bottleneck

Its outputs are highly dependent on the experience and industry knowledge of the analyst. The optimisation is not continuous. It is performed when the bottleneck is spotted, so when the performance incident occurs.

As mentioned earlier modern workflow systems gather a lot of data about performed processes, which might be used to tune those processes continuously and allow organizations to manage their capacity proactively rather than from incident to incident.

The answer to these analysts concerns could be the solution based on business process models they are used to and they can define and visualise and explain to the client – diagrammatic models like BPMN, UML, EPC or Petri Nets graphic representation.

It is unlikely that the algorithm will decide itself if a task is necessary or not in the process. Managers and engineers know well how a process should look like. The help is needed in choosing alternative paths and resources, and planning proper execution times for tasks to optimise the existing process according to multiple objectives i.e.: minimise process duration and cost, maximise return on investment and outputs quality.

The method presented in this paper uses Petri Nets to define the optimisation task – business process model and to simulate its execution. The simulation based optimisation [19] is used with a genetic algorithm NSGA-II (Non-dominated Sorting Genetic Algorithm II) [20] to find the Pareto front of optimal solutions. Paper describes the idea of using dynamic programming concept to decrease number of computations required when applying the change to the process.

Paper is divided into seven chapters. It starts form introduction were the purpose of the paper and the background of the this work is described. In the second chapter used genetic algorithm has been presented. It starts from defining the phenotype – business process model and its transition to genotype – chromosome, that is vector of numbers. After that, the idea of simulation based optimization with Non-dominated Sorting Genetic Algorithm is introduced. Third chapter focuses on Genetic Algorithm elitist approach and complexity. In chapter four the main innovation of this paper, that is the dynamic programming approach to business processes modelling is described. It contains the idea of how to divide bigger optimization task – more complex business process into number of smaller tasks – less complicated business processes and how to find improved solution for complex problem using solutions generated for the smaller sub-task – subprocesses. Fifth chapter shows the real life application of this method. The paper finishes with the discussion in chapter six and conclusions in chapter seven where the methods of business process modelling, analysis and optimisation presented are compared with other existing approaches and conclusions are made.

The purpose of this paper, except to present the genetic algorithm application, is also to focus the attention of researchers on the analysts’ commercial needs, as there is still a lot to improve in commercial used advanced business process optimisation methods.

• II.    Genetic Algorithm for Business Process Optimisation

• 2.1    Phenotype and genotype

Business process modelling notations since very beginning, first manufacturing process description by Adam Smith [21], are based on process being defined as a set of tasks, such as: materials storing, goods relocation, parts combining, functionality tests, client request verification etc.

The business process model composed of tasks and flows between them is a phenotype.

Task is characterised by preparation time and execution time, expenses (costs of materials, tools depreciation, salary etc.), inputs and outputs. Inputs represent all necessary resources, outputs - the results of the job and in some cases returned resources.

For the purpose of this paper Petri Net model of the task was used. It is composed of two transitions and a place between them (Fig. 1). The first transition simulates the start and the second the end of the task, while the place between them indicates if the task is being performed. Input places of the first transitions plays part of resources, the output places of second transitions are equivalent of the results.

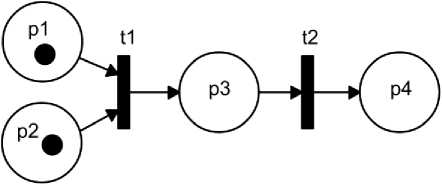
Fig. 1: Example of a task with two different resources and one product

The optimisation problem is represented by the genotype - a vector of transitions’ firing delays [22] and the sets of possible values for those delays defining the constraints.

5 = [ ti,..., tk ], ti G T^..., t2 G T2

Genotypes, from the genetic algorithm, are applied to the model, creating a phenotype that is the model of the process with set up task start and duration times. In a model time constraints, costs, profits and other necessary attributes are assigned to places and transitions. Data gathered during the simulation is used to estimate a value of a fitness function for each objective (f i (s)).

F ( 5 ) = [ f (5 ),..., f (5 )]

• 2.2    Simulation-based Optimisation

The idea of simulation based optimization is presented on the Fig. 2. Initializer starts the whole process by generating from the set of possible solutions S starting solution S₁ - first population in genetic algorithm. If this is first time the process is being optimised the heuristic approach has been applied and shortest possible t imes are set to transitions’ firing delays. Strong mutation at the beginning will provide diversity into the population. If this process has been optimised earlier last population can be used as a starting point S 1 .

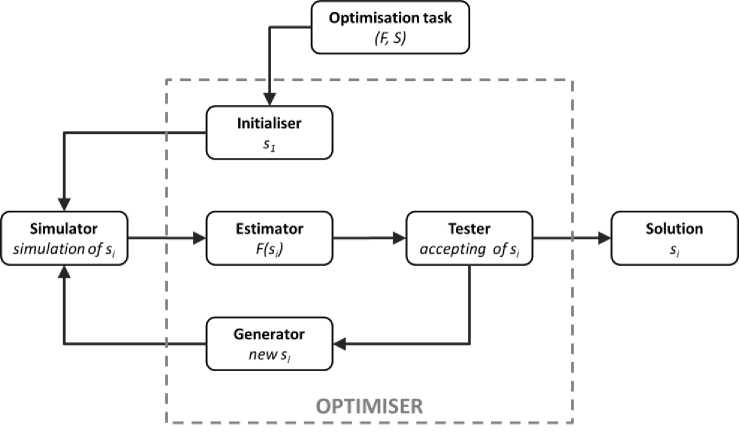
Fig. 2: Diagram of simulation based optimiser

The solution is used in the simulation. Transitions’ firing delays are applied to the model and data gathered by the simulator is used to estimate the fitness function value F(s). Based on fitness function value the selection is conducted and the decision about using the solution from population S 1 is made. If the solution is chosen the optimization process is stopped.

If not, the optimizer generates other possible solutions from the set S – next population S i . Next population is being generated using genetic algorithm operators: crossover and mutation.

Single point crossover operator is used. Chromosome can be divided only in points where genes responsible for single transition delay in business process model will not be separated. Otherwise the operator might produce incorrect genotypes. This way the knowledge about the phenotype – Petri Net business model is applied to improve the quality of reproduction.

Chromosomes for crossover are chosen using rank selection based on non-dominated sorting of NSGA-II algorithm. The concept is similar to roulette wheel but the probability is proportional to the rank – position in sorted collection of individuals. In NSGA-II individuals are sorted based on the solutions which dominates them and distance from the nearest neighbour.

Mutation probability is high at the beginning of the search to cover larger search space and it decreases over the time. This concept is similar to simulated annealing.

New population S i is then used in simulation and the next iteration begins.

• 2.3    Multiobjective optimisation in NSGA-II

For optimisation the elitist genetic algorithm NSGA-II was used. Even in the simplest form genetic algorithms are rather independent from the starting point and they can be used together with simulation results, when the goal function is not known or difficult to define.

In this method we need to find a set of nondominated solutions - individuals. The solution s is not dominated when it cannot improve any objective without degrading at least one another:

Therefore the complexity of the whole algorithm is O(mN ² ), where N is a size of the population and m is a number of objectives.

∀ s_n ≠ s : ∃ x : f_x ( s ) < f_x ( s_n )

Searching for this kind of set (called Pareto front) affects the selection method. Selection drives the population towards better solutions. In this case (NSGA-II [20]) better individual means:

• 1.   Not dominated,

• 2.   Dominated by less individuals,

• 3.   Lying further from other individuals.

The output from the optimisation will be a Pareto front S i describing a set of optimal solutions s i . Such a solution s i is composed of a vector of transitions firing delays – a genotype, together with estimated values of fitness functions vector F(s i ).

• III.    NSGA-II Algorithm Complexity

Most of genetic algorithms with non-dominated sorting for multi-objective optimisation have O(mN ³ ) computational complexity, there are some examples of elitist approach which allows to decrease the complexity to O(mN ² ), where N is a size of the population and m is a number of objectives. One example is used NSGA-II another is an approach from Rudolph [23].

In the NSGA-II algorithm each iteration starts from combining parent and children population.

Next the fast non-dominated sorting is applied, which includes finding for each individual number of dominating individuals and a set of dominated individuals, dividing the solutions to fronts according to the solutions which dominates them. Front 0 will contain non dominated solutions, front 1 solutions dominated only by the solutions from front 0 and so on. It requires O(mN ² ) comparisons.

Crowding distance is assigned to the elements of the calculated fronts. Calculating the distance from the nearest neighbours – by each of objective requires O(mN logN) operations.

The N best solutions become the next parent population. Better individual means individual assign to the front with the lower number (non-domination rank), or if the individuals belong to the same front – the individual with the higher crowding distance (lying further from other solutions) sorting and choosing the N best individuals form the whole population is O(2N log(2N)).

New children population is generated using selection, crossover and mutation.

• IV.    Application of the Dynamic Programming Approach

• 4.1    Dividing the Problem - scalability

Experiments [24] show that the genetic algorithm together with a simulator allows finding best model parameters (transition delays) to optimise chosen fitness function. It is obviously simple, but it is also time consuming. It takes a lot of operations O(mN ² ) to solve the problem – to create next generation. While the number of objectives (m) is dependent on the optimisation goals, the population size (N) and the number of generations are proportional to the number of parameters.

In this chapter the idea of using one of the Petri Nets features – scalability and the concept of dynamic programming to in the described simulation based optimisation is presented. Its goal is to divide the bigger optimisation task to set of smaller ones and reduce this way the number of necessary computations.

In a business process, elements like warehouses, factories, planes or ships can be found. Furthermore the same process can be analysed on a level of particular machines working on a production line or web services updating the database records. Model should be then very flexible when it comes to scalability, to be able to represent processes on any level of complexity.

Thank to this scalability, the process model can be divided into subprocesses or merged. From one point of view the whole engagement can be treated as a one task, while from another it can be complicated, multi-element process, just like in an example below (Fig 3).

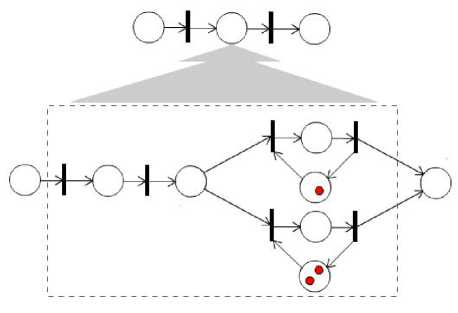
Fig. 3: Different complexity levels

This flexibility is not only useful for presentation reasons, but it also complies with all the requirements which must be fulfilled in case of the dynamic programming. The optimisation task in the form of a business process model can be divided into smaller sub-problems and their solutions can be merged into the overall solution.

This is one of the best practises of business process modelling, to model them as a high level – main p rocess containing activities and subprocesses defining those activities. This improves clarity of the process visualisation. Subprocesses can also be detected automatically by graph analysis, such algorithm should find in a graph sub-graphs that:

• 1.    Are composed of whole tasks. Tasks represented in a model by two transitions joined with a place cannot be told apart.

• 2.    Starts with one place or one transition (task starting transition) and ends as well with one place or transition (task end transition). This will allow replacing it by a single task.

• 3.    Incorporate a synchronisation of the flow for any flow fork it contains.

• 4.2    Dynamic Programming Procedure

Obviously choosing the best solutions for subprocesses and joining them together not necessarily gives the best overall solution. It might work fine when we have only one objective and it is time, then the faster task is done the better or at least not worse.

For the solution on a higher level, for the process that contains subprocesses, the same optimiser can be applied than to process without subprocesses. The Pareto front for the subprocess S i , found in a previous iteration will be used to evaluate the task, which represents this subprocess P i in next iteration, like on diagram (Fig. 4).

The genetic algorithm generates starting and ending transitions delays. Knowing the duration of the subprocess and having the Pareto front of possible solutions S i , the particular solution si and the estimated value of the fitness function F(s i ) can be found and used in the selection tournament method.

As an effect of the merging (optimising higher level process) the Pareto front with optimal solutions is being defined. It can be a final solution or an input for the next iteration.

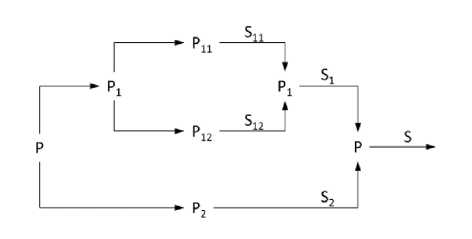
Fig. 4: Dividing problem (P) and merging solutions into final solution (S) - schema.

The procedure proposed in this paper consists of the following steps:

Step 1 Find in business process model P subprocesses P 1 -P _n ; in process P replace all subprocesses by single tasks to get the new model P’.

Step 2 For each subprocess P i in P 1 -P _n , if it is still has more tasks then set threshold, go through step 1) with P = P i .

Step 3 For each process P i , which does not contain any subprocesses find the set of non-dominated solutions S i using simulation based optimisation with genetic algorithm.

Step 4 For each process P i that consists of activities and subprocesses, for which solutions S has been already generated, find the set of non-dominated solutions S _i using simulation based optimisation with genetic algorithm. For simple activities use its attributes (i.e. cost, time constraints etc.) for estimation of fitness functions f. In case of tasks that are subprocesses replacements apply solutions S generated in previous iterations.

Step 5 Repeat step 4) until the solution S for the original business process P is reached.

• V.    Real life Example

This real life example purpose is to show how the designed optimization method can be used for continuous business process improvement, where it is most effective.

Social Insurance Institution in Poland has defined the way how to handle the sick-leave medical certificates. It contains 115 tasks for documentation validation, calculating, booking and payment of the compensation, communication with doctors, patients, employers and other insurers etc. The process has been redesigned, analysed and prepared to be implemented in an online e-health platform.

There were 3 main objectives: time, cost and quality measure connected to correctness of the compensation calculation and fraud detection.

If the whole medical certificates handling would be optimised using the proposed solution as a one process it’s complexity would be estimated: O(mN2), with m = 3 and N proportional to 115, as the population size in genetic algorithm should be proportional to the problem size.

The process has been designed in a form of 1 main process and 9 subprocesses having from 3 to 37 tasks, around 13 in average. It means that m equals 3 and average N is proportional to 13.

This procedure is designed for continuous process improvement; when the change will occur only changed subprocesses and the main process have to be recalculated.

Additionally the method calculates only once subprocesses that occur more than once in the whole process (i.e. formal acceptance procedure, quality check procedure).

• VI.    Discussion

The method seems to fit in the gap between analysts’ need of easy understandable method and results and researchers wish to work with the non-ambiguous models with mathematical basis. It has relatively simple graphic input in the form of diagram, which is used for simulation. Just like other visual notations transferable into executable, this can be considered as diagrammatic business process language (together with notations like BPMN, YAML and UML 2.0).

The Petri Net based business process model proposed in this paper also fulfils all the requirements of the mathematical business process model defined in example by Vergidis, Tiwari and Majeed [10].

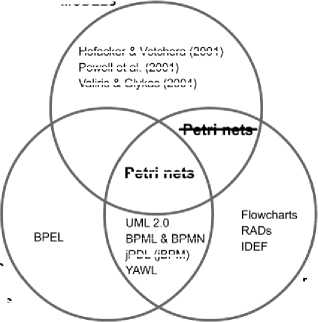
Vergidis, Tiwari and Majeed [3] have also published in IEEE a review and classification of existing methods for business process modelling. Proposed in this paper modelling method provides change to the classification of business process modelling techniques proposed by them (Fig 5). Petri net model can a business process language, which can be used to implement and simulate the execution of the processes.

MATHEMATICAL MODELS

BUSINESS

PROCESS LANGUAGES

Petri nets

UML 2 0

PDL(jBPM)

Powell el al. 2001

DIAGRAMMATIC

MODELS

Fig. 5: Amended classification of business process modelling techniques

Furthermore genetic algorithm and simulation based optimization can be added to the business process optimization types proposed by them in the review of existing business process modelling and optimisation techniques [3]. When diagrammatic models become graphic business process languages – as they can be compiled and executed in modern workflow software, researchers might place more attention to those two widely used modelling techniques. Analysts, supply chain managers, plant engineers and others would welcome guidance, new algorithms and methods.

Table 1: Amended classification of business process optimisation methods

Model of business process	Classification of the model	Types of business process analysis	Types of business processes optimisation
Flowcharts	Diagrammatic models	Observational
RADs	Diagrammatic models	Observational Performance analysis
IDEF	Diagrammatic models	Observational Simulation
Petri Net	Diagrammatic models Mathematical models Business process languages	Observational Validation Verification Simulation Performance analysis	Graph reduction Genetic algorithm and simulation
Mathematical models	Mathematical models	Performance analysis Simulation	Algorithmic approaches
Business          process languages	Business process languages	Performance analysis Simulation	Genetic algorithm and simulation

• VII.    Conclusion

Experiments described in earlier work [24] as well as work of others i.e.[10] show that the genetic algorithm is useful in the field of continuous parameter optimisation. It can be used to solve variety of problems, due to its robustness and its ability of escaping from local optima.

Together with simulation it can respond on analysts demand for relatively not complex tool based on diagrammatic business process notation for proactive capacity management. It is no capable of designing or reengineering the process but it can be used for continuous business process improvement and adaptation to new conditions and changes, which occur on the market and inside each company almost every day. The advantage of dynamic programming procedure is that it allows analysing and applying the innovation without recalculating everything from the beginning. Implementing the change of the situation on a market causes revision of only those subprocesses where the transformation takes place.

Results of this research might point researchers’ attention on the analysts’ needs and capabilities. Computer science should improve commercial used advanced optimisation methods by focusing on diagrammatic process languages as a basis for process improvement algorithms.