Dynamic Recurrent Wavelet Neural Network Observer Based Tracking Control for a Class of Uncertain Nonaffine Systems

Published Online October 2012 in MECS

System identification is an essential step while deriving state feedback controllers for uncertain nonlinear systems. Neural Networks (NNs) due to their universal approximation properties have proven to be an effective tool to deal with control problems of uncertain control systems [1]. Employment of neural network (NN) as an approximation tool in adaptive control strategies has greatly relaxed the constraint of linear parameterized nonlinearities and thereby broadened the class of the uncertain nonlinear systems which can be effectively dealt by adaptive controllers. In last few years, some researchers have developed the wavelet networks [2, 3]. Wavelet neural networks are feedforward neural networks using wavelets as activation function. A wavelet network consists of single layer of translated and dilated versions of mother wavelet function. Due to their space and frequency localization properties, the learning capability of WNN is superior to conventional neural networks. Training algorithms for WNN converge in smaller number of iterations than for conventional neural networks. These WNN combines the capability of artificial neural network for learning ability and capability of wavelet decomposition for identification ability. Thus WNN based control systems can achieve better control performance than NN based control systems [4-6].The feed forward structure of the conventional WNN limits the applicability of these networks only to static environmental conditions. These networks are not very effective under the frequently changing operating conditions and dynamic properties as they can not adapt rapidly under such circumstances. To overcome this problem, a feedback mechanism is inserted in conventional feed forward WNN giving rise to either recurrent WNN. These recurrent networks combine the properties of recurrence with the convergence properties of WNN to solve the complex control problems [7, 8].

System identification and subsequent controller design relies on the assumption of complete accessibility of system states, which is not valid in case of several real time systems. In case of such systems, where direct online measurement of system states is not feasible, observers are used for reliable estimation of systems states. Several nonlinear observer design schemes like high gain observers and sliding mode observers are cited in literature. However these schemes require the system uncertainties to satisfy certain admissibility criteria’s, such as norm boundedness condition leading to some conservative observer design [9-11]. Application of neural networks for nonlinear observer design is an effective strategy for state estimation. Neural network based observer designs relaxes the norm boundedness constraint of system uncertainties so estimate the states accurately and are applicable to a wide class of uncertain nonlinear systems [11-13].

In this work a dynamic recurrent wavelet network is used for designing a nonlinear observer for effective estimation of system states of an uncertain nonaffine system. To enhance the approximation property of the wavelet network, self recurrent architecture of wavelet network is used. Nonaffine system is first converted to an affine like form by applying a suitable transformation and then observer and controller schemes are designed for the later form by implicit function theorem [14, 15]. Finally the stability of the closed loop system and ultimate upper boundedness of closed loop signals is assured by constructing a Lyapunov function.

The paper is organized as follows. Section 2 provides the preliminary remarks. Section 3 formulates the problem. Section 4 addresses the designing and stability issues of wavelet observer design. State feedback controller design and main results are presented in Section 5.Effenciency of the proposed controller is illustrated in section 6 through a simulation study .Finally section 7 concludes the paper.

• II.    Preliminary Remarks

  • 2.1    Fundamentals of Wavelet Network

Wavelet network is a type of building block for function approximation. The building block is obtained by translating and dilating the mother wavelet function. Output of an n dimensional self recurrent wavelet network with m nodes is f — a T ф( x, ф, w, c ,0)

where x ^{e К} is the external input vector,

Optimal parameter vectors needed for best approximation of the function are difficult to determine so defining an estimate function as

Ф = tplxak c.0\ Айгй

Where                  and            are the

01 * w* c* 0*

estimates of ,   ,   , respectively. Defining the estimation error as

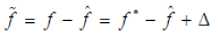
with a = a* -a, iv = i/ -u;c = c -c.9 = 8*-9^ = ср* -ф

By properly selecting the number of nodes, the estimation error f can be made arbitrarily small on f < f the compact set so that the bound           holds for allx eK.

Assumption A1

It is assumed that wavelet function and optimal values of wavelet parameters are bounded, so _thM    Н<^ф m     ,     И |< ^a-     ,

I w’ll < w*m |c 11 < c• m M| < Ф*. ,,.

f eK ^p

ф е Кm •       , + is the output vector,           is wavelet

mn        mn vector; w eK , c e R are dilation and translation

ф ( x , ф, w , c , 0 )

Wavelet vector                    is differentiable with respect to wavelet parameters a, w, c and 0.

vectors where as ^{ф e} represents the feedback input, this vector serves as the memory element and stores the previous information of the network. While

a e Rmxp

is the output weight matrix and

0e Rmn

is feedback weight vector.

2.2 Dynamic Recurrent Wavelet Networks

A dynamic recurrent wavelet network is governed by the following equation

Let

f ^*

be the optimal function approximation using

z — Az + Bu + a T ф ( z , ф, w , c , 0 )

an ideal wavelet approximator then

*              *T *

f — f + A — a ф + A

where     z ^eK      is    state    vector

A еК ^nxn , B еК ⁿ , u еК

with

.

ф =ф ( x , w , c ⁰ )      a‘, w\c *00

where                          and ,   ,   , the optimal values of a,w,c,0 respectively

are

and

A —[A,,...,A ] T

^{1       p}     denotes the approximation error

vector and is assumed to be bounded by

A * .

which ⁱ is a positive constant.

,in

This dynamic recurrent wavelet network architecture can be viewed as a closed loop system composed of a linear state space model and a nonlinear mapping realized by using a wavelet network. This architecture is particularly useful for designing of observers for uncertain nonlinear systems. Due to function approximation property of wavelet networks this observer design scheme accurately estimates the system states thereby reducing the estimation error to an arbitrarily small value over a compact set.

III. Problem Formulation

Considering a nonlinear non affine system of the form;

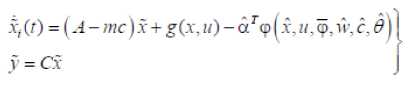
x ( t ) = f ( x , u )

Г

У = Cx

b   x (t) E% n where             are system states ,

u ( t ) E% is

bounded control input which will be designed to obtain f ( x u ) : % ^{n + 1} ^ % ⁿ .

desired tracking performance, , is a vector of smooth unknown nonlinear functions , y ^{( t} ) ^E % is measurable system output and c is the known output matrix.

Objective is to design an observer for accurate estimation of system states and to formulate a control law so that the tracking error

У = y — y where ^{x x x} and ^{У У У} are state and output estimation error respectively.

According to the approximation property of wavelet network, optimal wavelet approximation of g ( x , u ) can be expressed similar to (2)

g = a * ^T ф ( x , u , ф, w *, c * , 0 ) +A

so the observer error dynamics becomes

x.(r) = (Л-тС)х + a*⁷^{Ajy₇(pj/^c\ £*j + A

Cx

y     y ^d     converges to a small neighborhood of

У (t)

the origin. Here ^d     is the desired trajectory.

Desired trajectory is assumed to be smooth,

(Cn)

continuous      and available for measurement.

By      addition      and      subtraction

*T                   *    *    *

a  ф ( x , u , ф, w , c ,0 )

the above equation the form

(10) of

takes

Transforming the system into normal form

x ( t ) = Ax + Bu + g ( x , u )

У = Cx

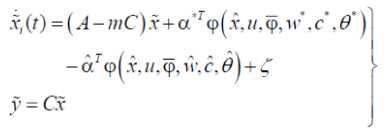
where

A E^ ^nxn

g ( x , u ) = f ( x , u ) — Ax — Bu

with

Z =

n and B E% are selected such that the pair

where

*T                   *    *    *

a  ф( x,u,ф,w ,c ,0 I — a ф(x,u,ф,w ,c ,0 ) + A

, is controllable and , is observable.

and is assumed to be bounded by m is a positive constant.

^m ,in which

IV. Dynamic Recurrent Wavelet Network based

Observer

4.1 Observer Design and Error Dynamics

For nonlinear system (6) with affine transformation (7), a dynamic recurrent wavelet network (5) based observer scheme can be formulated as :

4.2 Tuning Laws

Parameter adjustment mechanism for online tuning of wavelet parameters are derived using steepest descent method [16], for which the cost function is selected as

x;(r) = J.v-5»+ а7ф(х1г/,ч>,й,с:Й ) + m(y-v) у = Cx

^J = 2 У У

a^-^

yˆ where x and are estimates of system states and output respectively. m is the observer gain matrix

( A — mc )

selected such that            is a Hurwitz matrix.

!w = — г

Defining the observer error dynamics as

da

d J

² V d w

т

= -Г₁ V^r(p X,Z/,(p,W,C_?0 ы

T

I =—r₂ У ^с ^

c = -Г

d J Й ^T

³1 d £

where

t

I =-Г₄ y ^T A ,a A 4 ^T

V = - x ^T Px + - tr ( a ^T Г -' a ) + - tr ( w ^T Г^-1 w ) + - tr ( c ^T Г^-1 с )

2         2         '        2         ²       2         ³

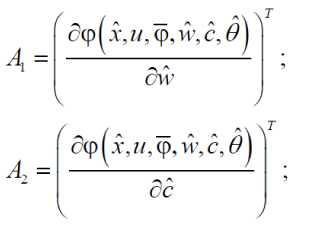
where P is symmetric positive definite matrix satisfying the following condition

( A - mC ) ^T P + P ( A - mC ) = - Q

for some symmetric positive definite matrix Q

.

Taking the derivative of ^V along the trajectories of the system

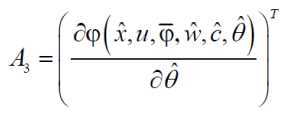
/^б^^+й^Г^^+т^с7^

A = C ( A - mC )⁴

After incorporating the modification term, the modified laws are

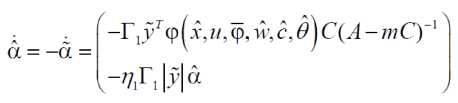
tr ( a ^T Г -' а ) + tr ( w ^T Г^-1 w ) + tr ( c ^T Г^-1 c ) + tr ( ё^т Г^-1 ^ )

Substituting adaptation laws in above equation

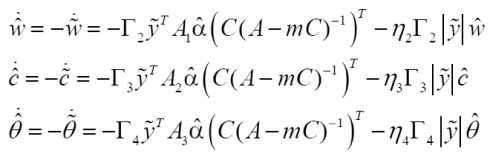
т

й^й^ (j7 ^а^ QA-/?£) ¹) +% | ^ й))+

к Г=Г ^t >  0  .      _   .

where i     i        is a constant design matrix representing the learning rates while i is a small

ti\ ^A^CCA~wQ *) +%|jjc))-/^(j^C^-^

2,

i = -,2,3,4 scalar design parameter with       ,  , ,

.

As these equations are composed of bounded variables and parameters, they can be viewed as linear systems with bounded inputs and this reflects the boundedness of wavelet parameters and their estimation errors.

1-K Ij] fita a))+z/₂1 j| /7(й^гй))+?;, l^/z^c))+т;₄1j| z?^ 9^

• 4. 3 Observer Stability Analysis

Consider the Lyapunov function of the form

Using the inequality

Above equation can be written as

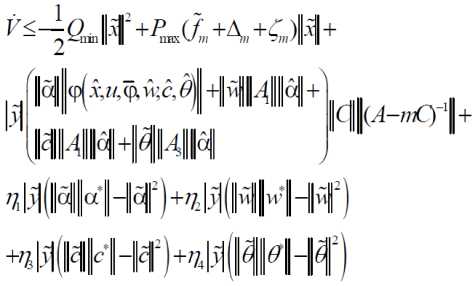
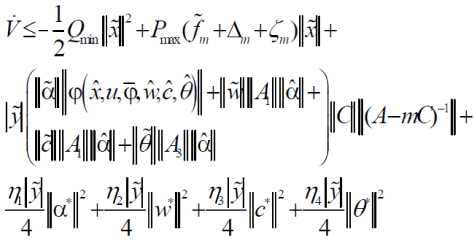
Thus we have the following result

Theorem : For the system of the form (6),under the condition of bounded input, a dynamic recurrent wavelet network based observer (8), constructed using wavelet functions satisfying assumption A1,with adaptation laws (13) has following properties

• a)    The state estimation error converges to the small neighborhood of origin.

• b)    Wavelet parameters are bounded.

Proof : Using the facts based on Lyapunov stability theory, inequality (15) implies that all the state estimation error with the proposed observer scheme for the system under consideration (6) converges to small neighborhood of origin. Tuning laws for the wavelet parameters indicate the boundedness of wavelet parameters.

Considering assumption A1 and boundedness of wavelet parameters, let their exist constants

^{1    2    3    4} such that

V. Controller Design

In this section a state feedback controller is constructed using estimated states and stability of observer system with respective control law is first examined and then stability issue of system under consideration is discussed [17].

M_x =imx(|ct|||(p(x,z^            =шк(||и||4|||6(||)

М> =m™(HHl№M« =ШК(ИИМ)

V г- 1 е _1 И f+ и. "г. +^ . + z. )| И +

I,y (M,+ M 2 + M 3 + M 4 )| |С|| ||( A - mC)-'||+ndyLf + SL.|f + ПЙ..,р + пМkif

4        max      4        max      4       max      4        max

5.1 Tracking Error Dynamics and Feedback Linearization

Defining a state tracking error vector for observer

e(t) e Жn as:

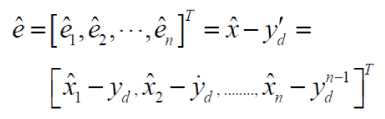
where

So the proposed observer design is stable as long as

Г          "-i T

"

and       ^L

T n

IIИ >

max m    mm

II C |² ( M_v + M ₂ + M ₃ + M ₄) 11( A - mC )^-111 + ^ L C la- 12  + S J C Il- If  + ’ J C I f -If +

4       max     4       max     4

n4 C k If k 4    11 llmax.

so the error dynamics of the system becomes

1Q min

e^ = (A - me") x 4- Bu +

Defining a filtered tracking error r ^еЖ as

u K = [ к, k2... к _,,1]T where        12 n 1     is an properly selected gain vector so that e ^ 0 exponentially as r ^ 0 [25].

Taking time derivative of filtered tracking error

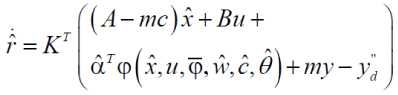
Defining the control law as

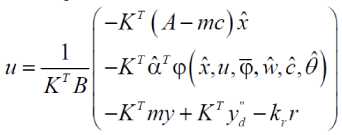
boundedness of all closed loop signals for the system under consideration with the proposed controller scheme.

Thus we have the following result

Theorem : All the closed loop signals for the system of the form (6), with proposed observer scheme (8) and control law (20), have following properties

• a)    The tracking error converges to the small neighborhood of origin.

• b)    All the signals in the closed loop system are uniformly bounded.

• 5.2 Stability Analysis

Proof : Using the facts based on Lyapunov stability theory, inequality (23) and (24) implies that all the closed loop signals of the system under consideration are uniformly bounded and the tracking error converges to small neighborhood of origin.

Consider the Lyapunov function of the form

V = - r

Taking the derivative of ^V along the trajectories of the system

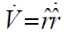
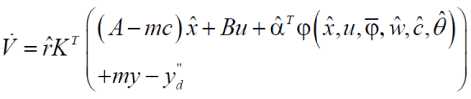
Substituting the control law in above equation

— ^кДг\

Thus with the proposed controller observer system is asymptotically stable.

To prove the boundedness of close loop signals for the system, consider the state tracking error vector e (t) g^ n e = [ e1, e2,---, enf = x ~ yd =

[x - yd, x2 - yd,........, xn - yd-1 ]T defined as

• VI.    Simulation Results

In this section, a simulation study is carried out to illustrate the efficiency of the proposed controller.

Consider the following nonlinear nonaffine system xx = .1 sin( xx) x32 + sin( x2) + x2

x2 = .1 cos(x2) x32 + sin(x3) + x3- u3

x ₃ = .5 sin( x ) cos( x ₂) x ₃ ² + .1 x sin( u ) + — + sin( u )

y = 3.35 x_x + 2 x ₂ + 2.1 x₃

System belongs to the class of nonlinear systems defined by (6) with n = 3 . Simulations were conducted with the dynamic recurrent wavelet network based observer design (8) and parameter tuning laws (13). Wavelet network with Mexican hat as the mother wavelet is used for approximating the nonlinear system dynamics while other observer matrices are selected as

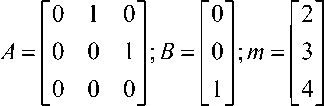
Controller is designed for the system using estimated states to achieve the desired tracking performance (20).

e = e + x

Asymptotic convergence of e to origin and boundedness of state estimation error to the small neighborhood of origin implies the uniform

Desired trajectory is taken as using

yd = .5sin t + .5cos t initial

x ( 0 ) = [ 0.75,0,0,0 ] ^T conditions

.Controller

K = [25,4,5,15]

parameter settings are                               .

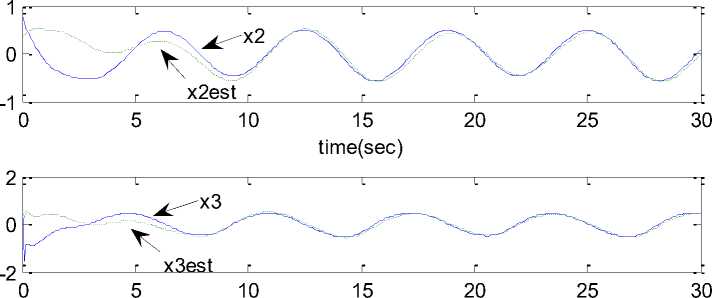
Simulation results shown in figure.1, 2 and 3, reflects the effectiveness of proposed observer – controller strategy, it can be seen that the actual and estimated system states effectively tracks the desired trajectory with a small steady state error.

time(sec)

time(sec)

Fig. 1: Actual and estimated system states

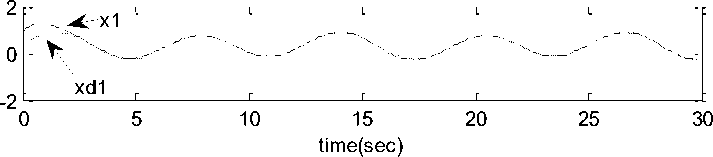
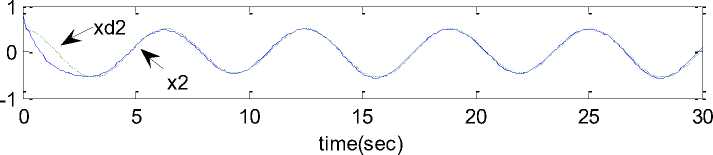
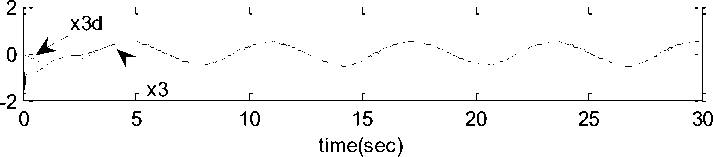
Fig. 2: Actual system states and desired trajectories

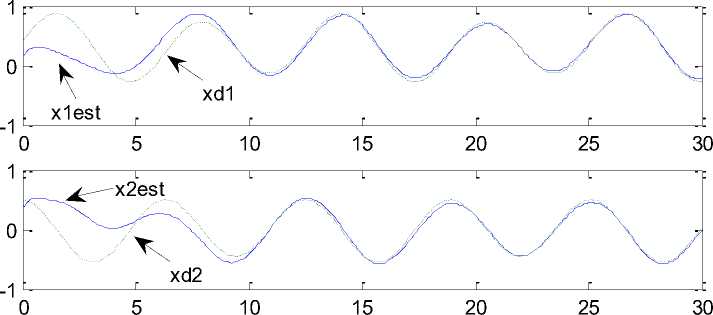
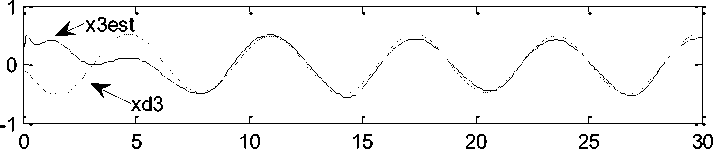
Fig. 3: Estimated states and desired trajectories

• VII.    Conclusion

In this work, a dynamic recurrent wavelet network observer scheme along with a tracking control strategy is presented for a class of uncertain, nonaffine systems. In this scheme a dynamic recurrent wavelet network is used to design a nonlinear observer .Adaptation laws are developed for the online tuning of wavelet parameters using using steepest descent method. Based on the estimated states, a state feedback control law is derived to achieve the desired tracking performance. The stability of closed loop system and ultimate upper boundedness all closed loop signals is proven using Lyapunov function. Finally a numerical simulation is carried out to show the effectiveness of proposed scheme.