Dynamic Vehicle Routing Problem: Solution by Ant Colony Optimization with Hybrid Immigrant Schemes

Published Online July 2017 in MECS

• I.    Introduction

  Dynamic Vehicle Routing Problem (DVRP) is the most challenging Vehicle Routing Problem (VRP) in logistics and transportation fields. VRP is a combinatorial optimization problem which identifies the optimal paths the vehicles can perform to satisfy the demands of customers under certain conditions such as each customer specified earlier should be visited only once and the capacity of the vehicles should not exceed the capacity limit [3, 4, 5, 9, 13, 17, 23]. The VRP concept introduced by Dantzig and Ramser in 1959 can be represented as a directed graph G (V, E), where V= {0, 1, 2,…, n} denotes the set of customers except for the node j=0 which represents the depot and E the edge between two customers [15, 16, 18, 25, 28].

DVRP which is a variant of VRP and a dynamic optimization problem dates back to Speidel (1976) and

Psaraftis (1980) [7, 18]. One of the objectives of DVRP is to minimize the distance travelled by vehicles when they are routed to customers exposed to dynamic environments. The dynamic changes may be due to dynamic requests by customers, the traffic jam of vehicles and vehicles breakdown [11]. In dynamic optimization problems, the optimum during dynamic changes is to be tracked [6, 19, 24, 26]. Meta-Heuristic methods such as Variable Neighborhood Search, Genetic Algorithm, Artificial Bee Colony and Particle Swarm Optimization were intensively experimented in the past years to solve dynamic optimization problems [6, 7, 8, 12, 27, 29, 33].

Ant Colony Optimization (ACO) algorithm, a meta -heuristic method that converges to better quality solutions in Static VRP was also used to solve Dynamic VRP [1, 11]. ACO achieved the capability to deal with dynamism by incorporating immigrant schemes [24]. One of the immigrant schemes, random immigrant when incorporated with ACO leads to high level of diversity. The proposed work focused on the proper balance of intensification and diversification capabilities of ACO algorithms. The algorithms HIACO-I, HIACO-II and HIACO-III were introduced in which the random immigrants and elitism based immigrants were hybridized in different proportions and integrated with ACO algorithm to solve DVRP. To evaluate the performance of the proposed hybrid algorithms, they were compared with other ACO algorithms incorporating immigrant schemes on different dynamic environments constructed from three well-known VRP instances.

The paper is divided into five sections; Section I gives a brief Introduction. Section II reviews Ant Colony Optimization. Section III introduces the Proposed Work and is divided into subsections Ant Colony Optimization with Hybrid Immigrant Schemes and Performance Analysis. The Section IV reports on Results and Discussion of the Evaluation and Section V provides the Conclusion.

• II.    Overview of Ant Colony Optimization

Ant Colony Optimization proposed by M.Dorigo is a Swarm intelligence based algorithm in which the behaviors of natural ants were considered in framing the algorithm [2, 14, 20, 30, 35]. In ACO algorithm, a population of ants (µ) is considered and each ant represents a solution of the problem to be solved [21, 22, 23, 24]. Ants start constructing the solutions from depot since vehicles are at the depot initially. Each ant chooses the next customer to be visited based on probability calculated in terms of pheromone trails (τ) and heuristic information .The probability of ant k, (pij ) to visit the customer j from customer i is given by the Equation (1).

Pij

={0

[ 4j ][2U] !

∑ _∈ N^ ^{[ T}u ] [ ^ij ^]

, Otℎerwise

, if j ∈ N^

where τ ij represents the existing pheromone trail on the edge between customers i and j and η ij represents the heuristic information available from distance between customers i and j (i.e., 1/dij). N represents the unvisited customers in the neighborhood of customer i for ant k. α and β are the parameters that determine the relative influence of pheromone trail and heuristic information respectively. If the selection of the next customer exceeds the vehicle capacity, then the vehicle returns to the depot and a new vehicle should begin the route from the depot. This process continues until all the customers’ requests are satisfied and thus an ant constructs a feasible VRP solution. When all the ants have constructed feasible solutions, it marks the completion of an iteration t and generation of population P (t). A short term memory with size denoted by ks is included in the pheromone matrix. The ks best ants of P (t) are added to short term memory at the end of iteration and modification of pheromone will be carried out. Ants follow the path rich in pheromone and converge to it. This is the stagnation property where the ants get trapped in confined regions and sometimes results in poor performance of the algorithm.

To avoid the stagnation property of ACO, various strategies such as local and global restart strategies, pheromone manipulation schemes, immigrant schemes, memory based methods and memetic algorithms have been adopted [22,23].The immigrant schemes such as random immigrant, elitism based immigrant and memory based immigrant were introduced to maintain diversity throughout the run. ACO with random immigrant (RIACO) performed too much diversification leading to diversification whereas ACO with elitism based immigrant (EIACO) and ACO with memory based immigrant (MIACO) generate guided diversity by transferring knowledge from previous environments [24].Afterward, Memetic algorithms (M-ACO) in which ACO algorithm hybridized with Local Search operator were introduced. Better intensification was achieved by the method, but diversification needed for dynamic optimization problems was not attained. Hence, a method in which M-ACO hybridized with random immigrant was adopted to achieve a balance between diversification and intensification .But it is stated that in some dynamic cases on which the method was applied, the diversity scheme destroyed the improvement achieved with Local Search operator [23, 21]. Therefore, ACO integrated with hybrid immigrant schemes methods were proposed to maintain a good balance between intensification and diversification of ACO and to make it suitable for dynamic optimization problems.

• III.    Proposed Work

The proposed work aimed at developing Ant Colony Optimization with hybrid immigrant schemes methods for dynamic vehicle routing problem. The performance of the proposed algorithms was evaluated on dynamic VRP instances constructed from three VRP instances. A comparative analysis with other ACO algorithms was also carried out.

• A. Ant Colony Optimization with Hybrid Immigrant Schemes

The methods in which immigrant schemes were hybridized and combined with ACO in three different manners have experimented. The methods in which immigrant schemes like random immigrants and elitism based immigrants were hybridized in different proportions and incorporated to ACO were considered as ACO with hybrid immigrant schemes (HIACO) [32].

In the first method, denoted as HIACO-I, random immigrants and elitism based immigrants were used in equal proportions, i.e., 50% each with ACO. The random immigrants help HIACO-I to handle diversity and elitism based immigrants to use knowledge from the previous environment in dynamic environments. Then the method HIACO-II was proposed where random immigrants have used in more proportion 75% together with 25% elitism based immigrants in ACO. The elitism based immigrants were used to reduce the randomness of random immigrants in slightly changing environments. The third method, HIACO-III was introduced in which 75% of elitism based immigrants and 25% random immigrants were hybridized and added to ACO. The random immigrants in HIACO-III make elitism based immigrants address significantly changing environments also. The various ACO algorithms with immigrant schemes were classified and as shown in Table 1.

The random Immigrants introduced by Grefenestette were generated randomly to replace the worst ants in the population. The number of immigrants generated would be ri,*ks , where ri denoted the immigrant replacement rate. To generate Elitism based Immigrants introduced by Yang; the best ant from the previous environment was selected. The swaps between customers of the same route of the ant were performed with a mutation probability pi .The ri,*ks elitism based immigrants generated from the previous environment P (t-1) would replace the worst ants in short-term memory [10, 24, 31, 33].

Table 1. Classification of ACO with Immigrant Schemes for DVRP

Ant Colony Optimization with Immigrant Schemes	Algorithm	Description
Ant Colony Optimization with Single Immigrant Scheme (SIACO)	RIACO	ACO with Random Immigrant
	EIACO	ACO with Elitism Based Immigrant
	MIACO	ACO with Memory Based Immigrant
Ant Colony Optimization with Hybrid Immigrant Scheme(HIACO)	HIACO-I	50% Random Immigrant & 50% Elitism Based Immigrant
	HIACO-II	75% Random Immigrant & 25% Elitism Based Immigrant
	HIACO-III	75% Elitism Based Immigrant & 25% Random Immigrant

B. Performance Analysis

The SIACO and HIACO algorithms were tested on dynamic test cases generated from VRP problem instances. The analysis focused on the effectiveness of HIACO algorithms to handle DVRP while establishing an equal importance to intensification and diversification factors .The best performance and diversity attained by an algorithm were mainly used to determine the effectiveness. The experiment design, performance measures and performance evaluation method considered are discussed below.

• 1) Experiment Design

The purpose of the experiments was to find out whether the proposed ACO algorithms maintains a good balance between intensification and diversification using hybrid immigrant schemes than other ACO algorithms with immigrant schemes on DVRP.

To carry out the experiments, Dynamic VRP instances were generated from three well known static VRP instances A-n32-k5, E-n76-k7 and F-n45-k4.The VRP instance, A-n32-k5 comes under “Class A” of Augerat et al instances. It is an instance with 32 customers and 5 minimum numbers of vehicles. The best value known for the instance is 784. E-n76-k7 belongs to “Class E “VRP instances proposed by Christofides and Eilon.E-n76-k7 is an instance with 76 customers and a requirement of 7 routes and its best value known is 683. F-n45-k4 is a “Class F “VRP instance proposed by Fisher. It contains 45 customers and 4 routes and its best value known is 724 [34].

The dynamic test cases were generated using Dynamic Benchmark Generator for Permutation Encoded Problem (DBGP) proposed by M.Mavrovouniotis. In DBGP, the dynamic changes were introduced by making modifications to the encoding of the static problem instance .For example, dynamic VRP test cases could be constructed by interchanging the location of a node with the location of another node in static VRP instance. The dynamic changes in DBGP depend on the magnitude of change, the frequency of change and dynamic change environment [24].The magnitude of change or change degree (m) is represented by a value that determines the number of swapped nodes. If the value of m is 0.25, it means that one fourth of the nodes can be replaced by other left out nodes in the problem instance. The frequency of change or change speed (f) denotes the number of times the nodes can be swapped. It depends on the algorithmic iterations. The dynamic change environment can be of random and cyclic change mode. The random dynamic environment is the one in which the reoccurrence of previously constructed dynamic environments in the current dynamic environment is not guaranteed. The latter one,cyclic dynamic environment can again be classified based on the way the base states of the dynamic environment are selected.If base state selection is in a logical ring fashion, it is called as reappear cyclically and referred as reappear randomly in random manner selection.

In the proposed work, DBGP parameters values were set as follows. The frequency of change was set as 10 and 100, the magnitude of change was given the values 0.25, 0.5 and 0.75 and the type of dynamic environments considered was Random (R), Reappear Random (RR) and Reappear Cyclic (RC). The number of base states used in cyclic dynamic environments was 4. So, the dynamic environment cycles 25 times when f=10 for 1000 iterations. For each instance, 18 dynamic environments were created.

The parameters of ACO algorithms with various immigrant schemes were initialized with values and those details are depicted in Table 2.

Table 2. Parameter Values used in SIACO and HIACO Algorithms for DVRP

Parameter	Value	Description
µ	50	Population size of ants
α	1	Parameter that determine the relative influence of pheromone trail ( τ )
β	5	Parameter that determine the relative influence of heuristic information (η )
k s	12	Size of Short term memory
r i	0.4	Immigrant ant replacement rate
pi m	0.01	Immigrant ants' mutation probability

2) Performance Measures

Offline performance, total diversity and execution time are some of the metrics used to evaluate the HIACO and SIACO algorithms and are defined below [21, 22, 23, 24].

Offline Performance is a measure to evaluate the performance of the algorithm and is given by the Equation (2).

^̅̅̅̅̅̅ = ; ^∑f=l * ; ∑7=1^ ∗ +              (2)

where G represents the total number of generations, R denotes the number of runs and P ^∗ represents the best fitness value after a change in generation i of run j.

Total Diversity measures the difference between the solutions in a population and is calculated using the Equation (3).

^̅̅̅̅̅̅ = _∑ f=l * I ∑ i=iDIV_tj + (3)

where G is the total number of iterations or generations, R is the number of runs and DIVij is the population diversity which is defined by the Equation (4).

DIV_tj = (^) ^∑P=1 ^∑ U^{s (} p ^, q ) (4)

where S (p, q) is the similarity metric .For VRP, S (p, q) is given by the Equation (5).

S (p,q)=1-(

\n*avg ( ⁿVp , n_Vq )

⁾         (5)

where CEpq are the common edges of the customers between the ant p and ant q, nv and nv are the numbers of vehicles used in the ant p and ant q. If the value of S (p, q) is 0, it means that the two ants are similar. A range of values between 0.6 and 0.8 is considered to be good since it means that the ants can communicate with dissimilar ants in a good manner.

Execution Time is the time taken to execute the algorithm. It corresponds to the CPU time or wall clock time. But the drawback is that it depends on various computer characteristics like hardware, operating system, language and compilers on which the algorithm is executed.

• 3)    Performance Evaluation

For performance assessment of proposed hybrid algorithms, they were compared with other ACO algorithms incorporating single immigrant scheme. The different dynamic test cases for evaluation were generated from each of the three VRP instances by varying the parameters such as change mode, change degree and change speed and it is shown in Table 3. In total, 324 experiments were conducted by SIACO and HIACO algorithms on 54 dynamic test cases.

In various dynamic environments, each algorithm was executed for 30 runs and 1000 iterations. The minimum distance obtained in each run and their corresponding iterations were noted. Then the smallest value from those minimum distance values was taken into account as the best solution. If that smallest distance value was obtained in more than one runs, then the run in which the smallest distance value was first noticed could be considered as the best run of that algorithm.

Depending on the best solution obtained by the algorithms, the algorithm that performed better was identified for each dynamic test case. The algorithm that produced the lowest value among the best solution of each algorithm was noted and considered as the algorithm that performed better than all other algorithms.

If different algorithms have produced the same lowest distance value on a particular dynamic test case, then the algorithm that performed better was decided on the basis of the best run of the algorithms. In case, the lowest distance value was obtained in the same run for different algorithms, then iteration in the particular run and execution time of the algorithm were also taken into account to determine the algorithm that performed better. For example, in a random dynamic environment created with f=100 and m=0.5, the best solution 813 was obtained by EIACO in iteration 531 of run 29 and by HIACO-III in iteration 557 of run 16. Then, HIACO-III was considered as the algorithm that performed better.

Table 3. Dynamic Test Cases generated from VRP Instances

Dynamic Test Cases	Dynamic Change Parameters
	Change Mode	Change Degree	Change Speed
1	R	0.25	10
2	RR
3	RC
4	R	0.5
5	RR
6	RC
7	R	0.75
8	RR
9	RC
10	R	0.25	100
11	RR
12	RC
13	R	0.5
14	RR
15	RC
16	R	0.75
17	RR
18	RC

For all dynamic test cases, the diversity value obtained in the best run and iteration of the better performed algorithm was also recorded. The SIACO and HIACO algorithms that performed better on 18 dynamic test cases (TC) of each of the three instances-A-n32-k5, E-n76-k7 and F-n45-k4 and values of their performance parameters such as distance (Dist.), diversity (Div.) and execution time (Time) along with the run (R) and iteration (G) in which it was first obtained are shown in Tables 4-6.

Table 4. Performance of SIACO and HIACO Algorithms on A-n32-k5 generated Test Cases

TC	Algorithm	Dist.	R	G	Div.	Time (s)
1	HIACO-I	814	22	327	0.648175	53.296
2	HIACO-I	817	11	649	0.666304	53.639
3	MIACO	817	25	663	0.653957	52.733
4	EIACO	815	13	332	0.639512	52.811
5	HIACO-III	813	17	786	0.682982	53.859
6	RIACO	813	13	774	0.734014	53.999
7	MIACO	817	30	692	0.745295	53.124
8	HIACO-I	815	17	297	0.658866	54.264
9	MIACO	820	4	838	0.606406	52.983
10	EIACO	813	8	691	0.613345	51.062
11	MIACO	813	2	403	0.580964	50.828
12	EIACO	806	17	262	0.637925	51.077
13	HIACO-III	813	16	557	0.654172	51.733
14	HIACO-I	813	7	513	0.639592	51.937
15	HIACO-II	813	27	891	0.580454	52.218
16	HIACO-II	810	23	352	0.748515	51.953
17	HIACO-II	810	23	352	0.748515	51.655
18	HIACO-I	811	21	243	0.678662	51.343

Table 5. Performance of SIACO and HIACO Algorithms on E-n76-k7 generated Test Cases

TC	Algorithm	Dist.	R	G	Div.	Time (s)
1	EIACO	733	3	580	0.501573	130.639
2	HIACO-I	740	14	948	0.580289	131.687
3	HIACO-III	733	17	970	0.535127	129.312
4	HIACO-III	736	23	470	0.517402	130.702
5	EIACO	745	10	510	0.552982	131.406
6	HIACO-III	739	10	437	0.591508	132.874
7	HIACO-I	730	8	649	0.641453	132.734
8	RIACO	742	24	487	0.6922	129.843
9	MIACO	742	1	967	0.5099	128.39
10	HIACO-III	728	24	791	0.417302	109.436
11	HIACO-I	730	5	682	0.498497	112.39
12	HIACO-I	730	13	198	0.460617	111.437
13	HIACO-III	720	29	183	0.544988	111.64
14	HIACO-III	720	29	183	0.346227	113.39
15	EIACO	727	8	255	0.478308	111.031
16	HIACO-III	727	14	674	0.356083	110.39
17	MIACO	733	20	980	0.40443	107.796
18	HIACO-III	718	24	682	0.417855	110.936

Table 6. Performance of SIACO and HIACO Algorithms on F-n45-k4 generated Test Cases

TC	Algorithm	Dist.	R	G	Div.	Time (s)
1	HIACO-III	755	12	899	0.409643	66.906
2	HIACO-II	762	8	843	0.624673	67.39
3	HIACO-II	769	22	136	0.616421	66.905
4	HIACO-I	732	24	140	0.38344	68.781
5	RIACO	759	4	297	0.666858	69.421
6	HIACO-II	762	20	384	0.651743	69.874
7	MIACO	733	25	17	0.490774	67.593
8	MIACO	731	4	775	0.476018	68.296
9	RIACO	731	15	129	0.459267	68.874
10	HIACO-I	762	23	881	0.647598	63.405
11	HIACO-III	764	22	826	0.570476	61.858
12	HIACO-III	758	11	692	0.511862	62.53
13	HIACO-I	758	2	618	0.476626	64.139
14	HIACO-I	760	16	662	0.660422	64.812
15	HIACO-II	766	22	609	0.644	66.484
16	RIACO	730	17	162	0.51065	64.109
17	HIACO-I	730	2	932	0.399579	62.249
18	RIACO	730	7	222	0.516399	62.608

• IV.    Results and Discussion

From the experiment results, it was observed that ACO with hybrid immigrant schemes performed better than ACO with single immigrant schemes in 63% of dynamic test cases and their better performance ratio is depicted in Figure1.

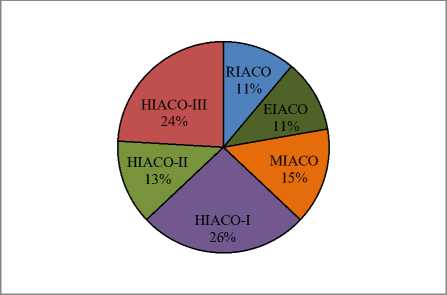
Fig.1. Performance Analysis of SIACO and HIACO Algorithms on DVRP Test Cases

■ A-n32-k5

■ E-n76-k7

■ F-n45-k4

SIACO and HIACO algorithms

Fig.2. Performance Analysis of SIACO and HIACO Algorithms on Dynamic Test Cases with respect to VRP Instances

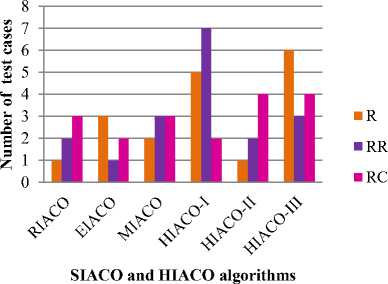
Fig.3. Performance Analysis of SIACO and HIACO Algorithms on Dynamic Test Cases with respect to Dynamic Environments

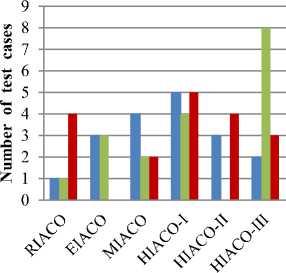
The number of dynamic test cases in which each SIACO and HIACO algorithms performed better considering VRP instances from which test cases were generated is shown in Figure 2 and based on type of dynamic environments is given in Figure 3.

HIACO-I performed better than all other algorithms on A-n32-k5 constructed dynamic test cases and its best performance was observed mainly in reappearing random dynamic environments. In the case of E-n76-k7 instance generated test cases, the outstanding performance was achieved by HIACO-III. The algorithm HAICO-III performed better mainly in random dynamic environments. HIACO-I also performed better than all other SIACO algorithms on E-n76-k7 dynamic test cases. Considering F-n45-k4 instance created test cases, HIACO-I performed better than all other algorithms. The better performance was obtained by HIACO-I in random dynamic environments on that instance.

It was observed that HIACO-III produced better results in random dynamic environments. HIACO-I performed better than all algorithms in reappear random dynamic environment irrespective of the instances. Based on the instance, HIACO-II and HIACO-III showed varying good results in the cyclic dynamic environment which reappears cyclically.

HIACO-I performed better than all algorithms on A-32-k5 instance generated dynamic environment with m=0.25 and f=10.In a dynamic environment with m=0.25 and f=100, HIACO-III performed significantly better than other algorithms on F-n45-k4 and E-n76-k7 generated instances. HIACO-III also performed better than all other algorithms on E-n76-k7 generated instance with m=0.5 for both values of f. For the dynamic environment with m=0.75 and f=100, A-n32-k5 generated instance produced better solutions by HIACO-II and HIACO-III produced better solutions on the instance created from E-n76-k7 in the same environment.

Considering the diversity factor, HIACO algorithms have obtained diversity values between 0.60 and 0.75 in almost all the dynamic test cases on A-n32-k5.But HIACO algorithms have attained diversity values in the good range only on a few dynamic test cases generated from other two instances. RIACO algorithms exhibited high diversity in all the dynamic test cases irrespective of the instances.

The execution time of algorithms increase as the size of the problem instances becomes big. Here, more execution time was taken by algorithms for E-n76-k7 dynamic test cases followed by F-n45-k4 and A-n32-k4 test cases. Similarly, more time were spent by algorithms for dynamic test cases with high frequency of dynamic change, i.e., f=10.

The intensification and diversification achieved by SIACO and HIACO algorithms were assessed in terms of lowest distance and corresponding diversity obtained in the particular run and iteration of the execution of the algorithm respectively. The intensification and diversification by SIACO and HIACO algorithms on various dynamic test cases generated from each of the three VRP instances are shown in Figures 4-9.

♦ RIACO ■ EIACO A MIACO X HIACO-I Ж HIACO-II о HIACO-III

Dynamic Test Cases

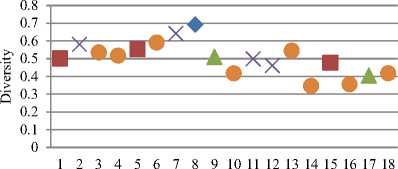
Fig.5. Performance Analysis of SIACO and HIACO Algorithms on A-n32-K5 generated Test Cases with respect to Diversification

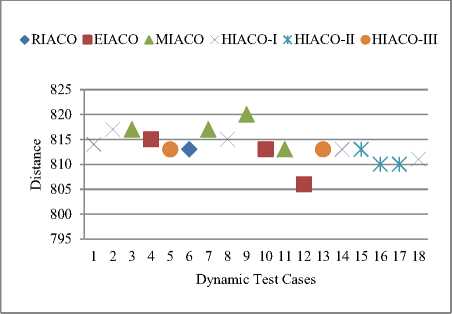
Fig.4.Performance Analysis of SIACO and HIACO Algorithms on A-n32-K5 generated Test Cases with respect to Intensification

♦ RIACO ■ EIACO А MIACO X HIACO-I Ж HIACO-II • HIACO-III

Dynamic Test Cases

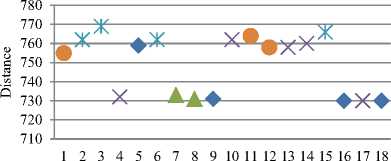
Fig.7. Performance Analysis of SIACO and HIACO Algorithms on E-n76-k7 generated Test Cases with respect to Diversification

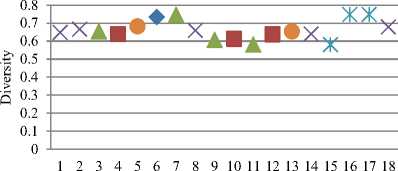
In A-n32-k5 instance generated test cases, the lowest distance values obtained by algorithms were in the range 810-820 and diversity in the range 0.6-0.8 in almost all the cases. HIACO algorithms have maintained a good balance between intensification and diversification in most of the cases.

♦ RIACO D EIACO АMIACO X HIACO-I Ж HIACO-II О HIACO-III

Dynamic Test Cases

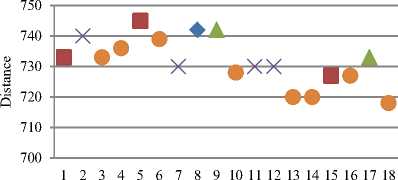
Fig.6. Performance Analysis of SIACO and HIACO Algorithms on E-n76-k7 generated Test Cases with respect to Intensification

The lowest distance values obtained by SIACO and HIACO algorithms on E-n76-k7 instance generated dynamic test cases lies in the range 720-745 and diversity values in the range 0.4-0.7 in almost all the cases. The algorithms were not able to achieve good diversification in E-n76-k7 instance except by HIACO-I and RIACO in one instance each. HIACO-III algorithms have shown a proper balance between intensification and diversification in a few cases only. HIACO-III algorithms with less diversity have better performance.

♦RIACO ■ EIACO АMIACO X HIACO-I Ж HIACO-II о HIACO-III

Dynamic Test Cases

Fig.8. Performance Analysis of SIACO and HIACO Algorithms on F-n45-k4 generated Test Cases with respect to Intensification

♦RIACO □ EIACO АMIACO X HIACO-I ж HIACO-II • HIACO-III

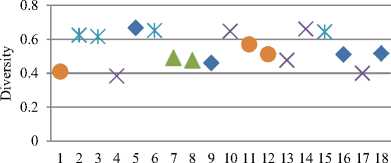
Dynamic Test Cases

Fig.9. Performance Analysis of SIACO and HIACO Algorithms on F-n45-k4 generated Test Cases with respect to Diversification

In F-n45-k4 instance generated dynamic test cases, the lowest distance values obtained by SIACO and HIACO algorithms were in the range 730-770 and diversity values in the range 0.4-0.7 in almost all the cases. The algorithms which showed good diversity values have lower performance only.

• V.    Conclusion

The proposed Ant Colony Optimization with hybrid random immigrant and elitism based immigrant schemes algorithms such as HIACO-I, HIACO-II and HIACO-III had performed better than Ant Colony Optimization with single immigrant scheme algorithms in many Dynamic Vehicle Routing Problem test cases. HIACO-III outperformed all other algorithms on E-n76-k7 instance generated dynamic test cases. When the type of the dynamic environments are considered, HIACO-III performed better in random dynamic environments whereas HIACO-I in reappear random environments and both HIACO-II and HIACO-III have shown good performance in reappear cyclic environments.

HIACO algorithms have maintained a good balance between intensification and diversification on A-n32-k5 instance generated test cases. It can be concluded that the performance of the algorithms is dependent on the problem instance and type of the dynamic environment. As future research directions, the parameters of the algorithms can be varied and applied on various dynamic environments. Moreover, ACO or any other metaheuristic methods integrated with various hybrid immigrant schemes can be attempted.