Economic Load Dispatch by Hybrid Swarm Intelligence Based Gravitational Search Algorithm

Автор: Hari Mohan Dubey, Manjaree Pandit, B.K. Panigrahi, Mugdha Udgir

Журнал: International Journal of Intelligent Systems and Applications(IJISA) @ijisa

Статья в выпуске: 8 vol.5, 2013 года.

Бесплатный доступ

This paper presents a novel heuristic optimization method to solve complex economic load dispatch problem using a hybrid method based on particle swarm optimization (PSO) and gravitational search algorithm (GSA). This algorithm named as hybrid PSOGSA combines the social thinking feature in PSO with the local search capability of GSA. To analyze the performance of the PSOGSA algorithm it has been tested on four different standard test cases of different dimensions and complexity levels arising due to practical operating constraints. The obtained results are compared with recently reported methods. The comparison confirms the robustness and efficiency of the algorithm over other existing techniques.

Еще

PSOGSA, Economic Load Dispatch, Ramp Rate Limits, Prohibited Operating Zones (POZ)

Короткий адрес: https://sciup.org/15010450

IDR: 15010450

Текст научной статьи Economic Load Dispatch by Hybrid Swarm Intelligence Based Gravitational Search Algorithm

Published Online July 2013 in MECS DOI: 10.5815/ijisa.2013.08.03

Economic Load Dispatch (ELD) Problem determines the schedule of generation which minimizes the total generation and operation cost while satisfying the load demand and operational constraints of all generating units. As this problem is having a both complex and nonlinear characteristic with heavy equality and inequality constraints [1].However modern generating units have higher order non-linearities and discontinuities in input-output characteristics due to valve point loading, ramp rate limits and prohibited operating zones[2]-[4], which makes the finding of optimal solution very hard.

Classical optimization methods such as lambda iteration, base point and gradient method [5]-[6] were employed to solve the ELD problem. Lambda iteration method is the most commonly used, but for the effectiveness of this method, the formulation needs to be continuous. Dynamic programming [7] has been used to solve ELD problem with valve point effect but it is time consuming, computationally extensive and unnecessarily increases the dimension of the problem.

Due to the inadequacy of these methods to stuck to the local solution instead of global ones, artificial intelligence techniques are used to solve ELD problem, these techniques include Genetic algorithm (GA) [8], Particle Swarm (PSO) [8], Evolutionary Programming (EP) [9], Differential Evolution (DE)[10], Hopfield neural network (HNN)[11]. Other techniques are New Particle Swarm with Local Random Search (NPSO_LRS)[12], Self-Organizing Hierarchical Particle Swarm Optimization (SOH_PSO)[13], Bacterial Foraging Optimization Nelder Mead Hybrid Algorithm (BFONM)[14], Biogeography based optimization (BBO) [15], continuous Quick Group Search Optimizer (QGSO) [16], Chemo tactic Differential Evolution Algorithm (BF_DE hybrid)[17], Hybrid swarm intelligence harmony search (HHS)[18], Firefly algorithm (FA)[19], Artificial bee colony optimization(ABC)[22].These optimization methodologies have been applied successfully to solve economic load dispatch problem.

Here, a new population based hybrid algorithm (PSOGSA) is implemented to solve economic dispatch problem. The PSOGSA algorithm incorporates some features of particle swarm optimization algorithm into gravitational search algorithm i.e. exploitation ability of PSO with ability of exploration in GSA to unify their strength. The agents are initialized randomly and each agent in the search space is attracted towards the agent having a good solution. The agents near the optimal solution moves more slowly and assures the exploitation step of algorithm. Here gbest is used to exploit the global best. The position and velocity are updated until it reaches to the stopping criterion.

To validate the effectiveness of PSOGSA algorithm ELD problem with smooth and non-smooth cost function are considered in this paper. Non- smooth cost function includes generator capacity constraints, ramp rate limits, prohibited operating zones and losses whereas smooth cost function considers generator capacity constraints and power balance constraints with and without power loss.

The paper is organized as: sections 2 emphasize on the ELD problem with various practical constraints, section 3 gives a brief description about the PSOGSA algorithm. Section 4 presents the implementation of PSOGSA for ELD problem. In section 5 simulation results for our test cases are compared with the other recently reported methods. Finally the conclusion is drawn in section 6.

max(pmin,UR -p) < p < min(pmax,p0 -DR)

Where Pi is the current output power of ith unit and Pio is the power generation of ith unit at previous hour and URi and DRi are the up and down ramp rate limits respectively.

II. Problem Formulation
2.1 Power Balance Constraints:

The aim of economic load dispatch problem is to minimize the overall cost of production of power generation while satisfying power balance, generator constraints with ramp rate limits and prohibited operating zones. The objective function is usually stated as quadratic function. Mathematically the problem is formulated as:

min f = E N G F ( p i ) (1)

where

F ( p i ) = ap ² + bp + C i (2)

Where F i is the total generating cost of i^th generating unit and a i , b i and c i are the coefficients of i^th generator. P i is the real power output (MW) of i^th generator corresponding to time t, N_G is the total number of generating units. The ELD problem discussed is subjected to the following constraints:

У ^N G p = p + p

4—11 = 1 i ^D L

Where PD is total load demand and PL is the total transmission loss. PL is calculated using B- coefficients, given by-

E Np N_r

^GGPB P (4)

i = 1 4—1 J = 1 ^l 4 J ^v ’

2.2 Generator Constraints:

The power output of each unit is restricted by its upper Pmax and lower Pmin limits of real power generation and is given by- min

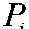
max

2.3 Ramp rate limits:
2.4 Prohibited Operating Zone:

When the ramp rate limits are considered, the generator operation constraints (5) are modified as follows:

A unit with prohibited operating zone has discontinuous cost characteristics. So the unit operation is avoided in prohibited zones. The concept of prohibited operating zone considers the following constraints:

F min < p < p L (I = 1,2,..., n_g )

i ,1

p"—1

N ) ^ (7)

Where P i ^U j-1 and P i ^L j are the upper and lower boundaries of j^th prohibited zone of i^th generator and N Zi is the number of prohibited zones of i^th generator.

III. Hybrid Algorithm (PSOGSA)

PSOGSA is formulated by S. Mirjalili et al. in 2010[20]. The basic concept behind the hybridization is to combine the ability of social thinking (gbest) in PSO using the local search capability of GSA.

The proposed algorithm considers the agents as objects and the position of ith agent is given by-

X, = ( x 1 ,..., x d ,..., x n )l = 1,2,..., N (8)

Where x i ^d is the position in the d^th dimension of the i^thagent (mass).

The masses are described randomly and the force acting on mass i from mass j is given as

, M_t ( t ) x M, ( t ) ,

f * ( t ) = g ( t ) ^l'; ^jV’ ( x d ( t ) - x d ( t )) (9)

j R j ( t ) + c ^J

Where Mi (t) and Mj(t) are masses of objects I and j, G(t) is the gravitational constant at time t, ε is a small constant, Rij(t) is the Euclidean distance between I and j objects.

R j( I ) = | X l ( t ), X j ( t )||₂ (10)

Gravitational constant G (t) is initialized randomly in the beginning and is reduced with time to control the search accuracy.

t a

G ( t ) = G o e^T (11)

It means G is the function of time t and initial value G0, where G0 is the initial value of gravitational constant, α is the user specified constant and T is the maximum number of iterations and t is the current iteration.

Let the total force acting on agent i in the dimension d is described as-

M_t( t ) =

m _z ( t ) * 5 Z n = 1 m , ( t )

Where current-fitness i (t) is the fitness value of the agent i at any time t, and best (t) and worst (t) are the minimum and maximum fitness value of all agents.

The agents exploring in the search space are attracted towards other agents by means of gravity force and causes a movement to the agents having heavier mass. The heavier mass represents a good solution. Here gbest help them in finding the optima around a good solution. The optimal solution is found by using the exploitation ability of PSO. Global search and local search balance is accomplished by adjusting the values C1 and C2.

F id ( ¹ ) = Z N .„„r^nd ^ FF ( t) (12)

Where, rand j is a random number between the interval [0, 1].

The acceleration of ith agent at iteration t having d dimension is given by the law of motion- acd (t) =

F ^d ( t )

M i ( t )

The velocity of an agent is calculated as- vd (t +1) = w.v (t)c. x rand x acf (t)

i _' i 1 _d i ₍₁₄₎

+ c ₂ x rand x (gbest - x_t ( t ))

Where v_i^d(t) is the velocity of agent i at iteration t in dimension d, c j ´ is a weighting factor, w is a weighting function, rand is a random number between 0 and 1, αc i ^d(t) is the acceleration of i^th agent at iteration t in dimension d and gbest is the best solution found so far.

At each, iteration the position of an agent is calculated as- xd (t + 1) = xd (t) + vd (t +1) (15)

Where vid(t+1) is the velocity of next agent and xid is the position of ith agent in dth dimension at iteration t.

The value of masses of agents are calculated by comparison of fitness- mi(t) = currentfitnesst (t) - 0.99 * worst(t) best(t) - worst(t)

i = 1,2,..., n

IV. Implementation of PSOGSA Algorithm for Economic Load Dispatch

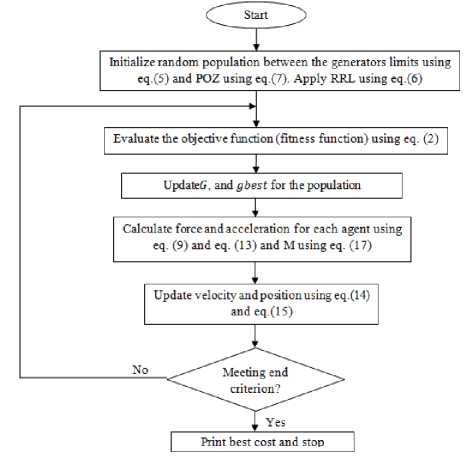
Fig. 1: Flow chart of PSOGSA approach for ELD

Step1: Search space identification

In this agents are randomly initialized and located between the minimum and maximum operating limits of generators. Each agent should satisfy the constraints given by “(3)” and “(5)”.

Step 2: Fitness evaluation

This evaluates fitness for each agent using “(2)” while constraints are satisfied. Update G and gbest for the population.

Step 3: Agent force calculation

In this total force acting on agent i in different dimensions is calculated using “(9)”.

Step 4: Evaluation of mass and acceleration of an agent

The acceleration of ith agent in d dimension is calculated using “(13)” and mass is calculated using “(17)”.

Step 5: Update velocity and position of agents

The next velocity of agent is calculated using “(14)” and position is updated using “(15)”.

Step 6: Stopping criteria

Repeat process 2 to 5 until stopping criteria is met.

In this paper maximum number of iterations is the stopping criteria. The step by step process involved to solve ELD problem using PSOGSA approach is shown with the help of flow chart in figure 1.

V. Case Studies and Numerical Results
5.1 Test case I: Six unit system

The system contains six generating units. The input data for this system is taken from [8]. The load demand is set as 1263 MW. In this system transmission loss, POZ and ramp rate limits are also considered. The experimental result obtained from PSOGSA approach, Hybrid SI based Harmony Search (HHS) [18], and Biogeography Based Optimization (BBO) [15] and Self-Organizing Hierarchical Particle Swarm
5.2 Test case II: Eighteen unit system
5.3 Test case III: Twenty unit system

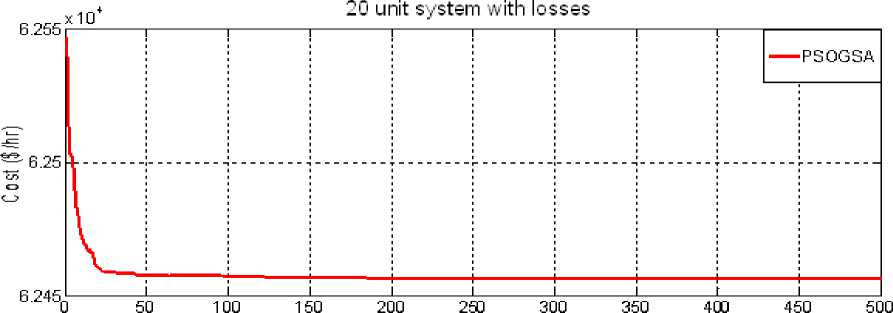
The system contains twenty generating units with loss coefficients. The input data for this test system is taken from [11].The system load demand is 2500 MW. The obtained results in terms of optimum power output and power loss using PSOGSA approach has been compared with General Algebraic Modeling System (GAMS) [24], Biogeography Based Optimization (BBO) [15] and other methods are shown in Table 4. Convergence characteristic of the 20 unit system with loss is shown in (4).
5.4 Test case IV: Fifty four unit system

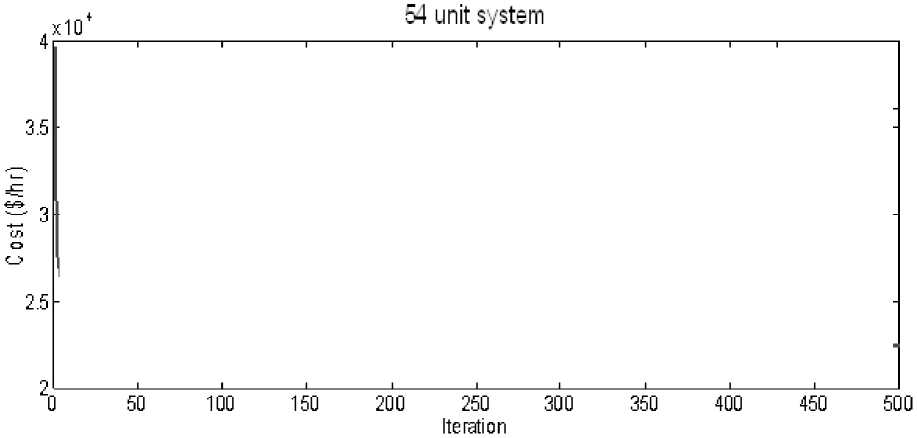
A large scale IEEE 114 bus system consisting of 54 generating units is considered here. The load demand is set to 4242 MW. The input data for this system is taken from Dieu et al . 2012 [25]. The optimum power output achieved by PSOGSA is presented in Table 5. The minimum cost obtained is compared with Augmented Lagrange Hopfield Network (HN) [25], Differential evolution (DE) [25], particle swarm optimization (PSO) [25]. A convergence characteristic of 54 unit system is shown in (5).

To validate the effectiveness of hybrid PSOGSA approach, four standard test cases having different properties were considered. These are a 6 unit system with POZ and ramp rate limits, an 18 unit system with varying percentage of maximum demand, a 20 unit system with losses and a large scale 54 unit system. The algorithm is implemented in MATLAB 7.8 and the system configuration is Intel core i3 processor with 2.3GHz speed and 2GB RAM.

Optimization (SOH_PSO) [13] are shown in Table 1. (2) shows the convergence characteristic of the six unit system with ramp rate limits, POZ and losses.

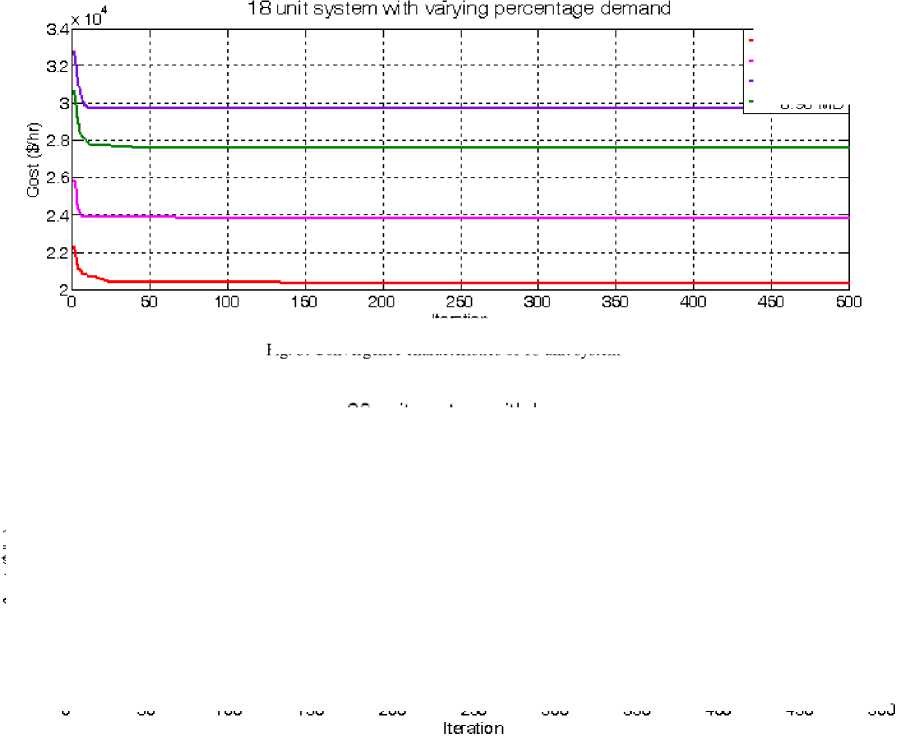
This test case contains Crete Island system of 18 generating units. The input data for this test case is taken from [21], and the maximum power output for the system is 433.22MW. The simulations were carried out with varying percentage of maximum power demand. Their best solutions using PSOGSA are shown in Table 2. The result obtained from PSOGSA approach, simulated annealing (SA) [23], artificial bee colony (ABC) [22] and other techniques is listed in Table 3. The convergence characteristics for eighteen unit system obtained by PSOGSA approach is shown in (3).

Unit	SOH-PSO	BBO	HHS	PSOGSA
Pg1	438.21	447.3997	449.9094	447.5144
Pg2	172.58	173.2392	172.7347	173.1461
Pg3	257.42	263.3163	262.9643	263.3337
Pg4	141.09	138.0006	136.03	138.9189
Pg5	179.37	165.4104	166.967	165.3541
Pg6	86.88	87.07979	86.8778	87.1269
O/P (MW)	1275.55	1275.446	1275.4832	1275.3941
P loss	12.55	12.446	12.4834	12.39404
Cost($/hr)	15446.02	15443.0963	15442.8313	15442.3931

		6 unit system with FiRL, POZ and losses
			PSOGSA

5. S 1.55 1 545
5. S 1.55 1 545

¹-^Ы0	50 1 00 1 50 2 00 2 50 30 0 8 50 400 4 50 500

Iteration

Fig. 2: Convergence characteristics of 6 unit system

Table 2: Results for eighteen unit system using PSOGSA

Unit	0.70*MD	0.80*MD	0.90*MD	0.95*MD
Pg1	15.0000	15.0000	15.0000	15.0000
Pg2	44.6316	45.0000	45.0000	45.0000
Pg3	25.0000	25.0000	25.0000	25.0000
Pg4	25.0000	25.0000	25.0000	25.0000
Pg5	25.0000	25.0000	25.0000	25.0000
Pg6	3.0000	3.0000	8.2149	13.7055
Pg7	3.0000	3.0000	8.2195	13.7069
Pg8	12.2800	12.2800	12.2800	12.2800
Pg9	12.2800	12.2800	12.2800	12.2800
Pg10	12.2800	12.2800	12.2800	12.2800
Pg11	12.2800	12.2800	12.2800	12.2800
Pg12	14.8842	20.7256	24.0000	24.0000
Pg13	3.0000	3.0000	3.1481	6.4138
Pg14	21.1318	30.8653	36.2000	36.2000
Pg15	23.2361	32.3543	42.4920	45.0000
Pg16	24.1260	33.2650	37.0000	37.0000
Pg17	24.1243	33.2458	43.3525	45.0000
Pg18	3.0000	3.0000	3.1510	6.4127
O/P(MW)	303.254	346.576	389.898	411.5589
Min cost ($/hr)	20386.2157	23855.2865	27653.7507	29731.0666
Avg. cost ($/hr)	20386.2360	23855.28655	27653.7893	29731.0666
SD	0.0372	0.0001	0.0253	0.0000
Time/Iter (sec)	0.0280	0.0215	0.0187	0.0158

Table 3: Comparison of results (18 unit system MD=433.22MW)

Method	0.70*MD	0.80*MD	0.90*MD	0.95*MD
λ_ Iteration	20393.48	23861.58	27652.47	29731.05
Binary GA	20444.68	23980.24	27681.05	29733.42
RGA	20396.39	23861.58	27655.53	29731.05
ABC	20391.60	23589.40	27653.60	29730.80
SA	20386.309	23855.855	27653.78	29731.066
PSOGSA	20386.2157	23855.2865	27653.75	29731.066

---0.70 "MD

---0.80 "MD

---0.95-MD

---0 90-MD

Iteration

Fig. 3: Convergence characteristics of 18 unit system

Fig. 4: Convergence characteristic of 20 unit system

Table 4: Result of 20 unit systems with losses

Unit	BBO	GAMS	QGSO	PSOGSA
Pg1	513.0892	512.782	512.7303	512.7788
Pg2	173.3533	169.102	169.0263	169.0469
Pg3	126.9231	126.891	126.8806	126.8915
Pg4	103.3292	102.867	102.8723	102.8666
Pg5	113.7741	113.683	113.6836	113.6839
Pg6	73.06694	73.572	73.5741	73.5798
Pg7	114.9843	115.290	115.3037	115.2981
Pg8	116.4238	116.400	116.4090	116.4039
Pg9	100.6948	100.405	100.4303	100.4041
Pg10	99.99979	106.027	106.0581	106.0575
Pg11	148.977	150.239	150.2337	150.2512
Pg12	294.0207	292.766	292.7813	292.7548
Pg13	119.5754	119.114	119.1165	119.1124
Pg14	30.54786	30.832	30.8179	30.8350
Pg15	116.4546	115.805	115.8179	115.8097
Pg16	36.22787	36.254	36.2542	36.2548
Pg17	66.85943	66.859	66.8611	66.8649
Pg18	88.54701	87.971	87.9696	87.9650
Pg19	100.9802	100.803	100.8088	100.7982
Pg20	54.2725	54.305	54.3106	54.3083
P Loss	92.1011	91.967	91.965	91.9654
O/P (MW)	2592.1011	2591.967	2591.965	2591.9654
Min Cost ($/hr)	62456.7926	62456.633	62456.6330	62456.63309

Table 5: Result of 54 units System

Unit	PSOGSA	Unit	PSOGSA
Pg1	30.0000	Pg30	80.0000
Pg2	30.0000	Pg31	46.4558
Pg3	30.0000	Pg32	30.0000
Pg4	30.0000	Pg33	20.0000
Pg5	150.0000	Pg34	20.0000
Pg6	156.0356	Pg35	100.0000
Pg7	30.0000	Pg36	88.2642
Pg8	100.0000	Pg37	150.0000
Pg9	30.0000	Pg38	30.0000
Pg11	30.0000	Pg39	234.5160
Pg12	100.0000	Pg40	212.3911
Pg13	124.5674	Pg41	20.0000
Pg14	30.0000	Pg42	50.0000
Pg15	30.0000	Pg43	100.0000
Pg16	69.8064	Pg44	196.1548
Pg17	30.0000	Pg45	100.0000
Pg18	86.6968	Pg46	20.0000
Pg19	30.0000	Pg47	58.1562
Pg20	30.0000	Pg48	86.0867
Pg21	92.5384	Pg49	20.0000
Pg22	108.1637	Pg50	50.0000
Pg23	100.0000	Pg51	100.0000
Pg24	100.0000	Pg52	100.0000
Pg25	132.5493	Pg53	100.0000
Pg26	77.0648	Pg54	50.0000
Pg27	100.0000	Min Cost ($/hr) Time/Iter (sec)	22432.2510 0.0416
Pg28	100.0000
Pg29	156.8691

									--PSOGSA

Fig. 5: Convergence characteristic of 54 unit system

Parameter Selection

There are four important parameters in the hybrid PSOGSA algorithm: Gravitational constant (G0), acceleration coefficient (α), weighting factor (C1, C2) and population size (n). These parameters are selected in such a way that a smooth convergence behavior is ensured. To obtain the optimal values of these parameters a detailed study was carried out by varying these parameters. For each combination 20 trials have been made with maximum number of iterations set to 500 per trial. Performance of PSOGSA is analyzed for a large scale 54 generating unit ELD problem.

Table 6: Effect of weighing factor C1 and C2 on Case 4 (20 trials)

Case	C1	C2	Min cost ($/hr)	Avg cost ($/hr)	Max cost ($/hr)	SD
1.	1.0	1.5	22432.3168	22432.5327	22432.4247	0.1079
2.		2.0	22432.3443	22436.2074	22434.2758	1.9315
3.		2.5	22432.2529	22452.2598	22442.2563	10.003
4.	1.5	1.5	22432.6282	22436.4184	22434.5233	1.8950
5.		2.0	22432.2665	22432.3059	22432.2862	0.0196
6.		2.5	22449.3487	22458.2204	22453.7845	4.4358
7.	2.0	1.5	22432.2510	22432.3347	22432.2928	0.0418
8.		2.0	22432.2674	22432.3018	22432.2846	0.0172
9.		2.5	22432.2529	22432.2561	22432.2545	0.0016
10.	2.5	1.5	22432.2709	22432.3706	22432.3207	0.0498
11.		2.0	22432.2671	22432.2817	22432.2744	0.0073
12.		2.5	22432.2641	22436.2362	22434.2501	1.9860

The optimum parameters are selected as follows: population size (n=10), gravitational constant (G0 ) =1 and acceleration coefficient (α)=10 are initially considered. To analyze optimum value of weighting factor c1 and c2; the values of C1 varied between 1.0 and 2.5 with a step increase of 0.5 and C2 is varied from 1.5 to 2.5 with a step increase of 0.5. The results of variation in C1 and C2 for obtaining minimum, maximum and average costs and the standard deviation for 20 trials are shown in Table 6. Best results were obtained when C1=2.0 and C2=1.5.

Table 7 lists the effect of acceleration coefficient α on the performance of the algorithm. Too large α is not capable in searching the minimum for the problem in addition to this it reduces the computational speed of the algorithm and increases standard deviation. For repeated 20 trial α=10 resulted in achieving optimal solution.

Table 7: Effect of α on 54 unit System (case 4, 20 trials)

Sr.No	α	Min cost ($/hr)	Max cost ($/hr)	Avg cost ($/hr)	SD
1.	10	22432.2510	22432.3347	22432.2928	0.0418
2.	100	22455.3955	22550.7479	22503.0717	47.6761
3.	1000	23717.9908	23890.5514	23804.2711	86.2809

Table 8: Effect of population size on 54 unit system (case 4, 20 trials)

Sr.No	n	Min cost ($/hr)	Max cost ($/hr)	Avg cost ($/hr)	SD
1.	50	22432.3948	22432.4233	22432.4085	0.0142
2.	100	22432.2510	22432.3347	22432.2928	0.0418
3.	150	22432.4186	22432.4223	22432.4204	0.0018
4.	200	22432.3456	22432.7407	22432.5431	0.1975

Table 8 depicts the performance of PSOGSA algorithm for different population sizes. Test was carried out for repeated 20 trials with population size 50, 100, 150, 200.The study shows that too large population size makes the algorithm slow whereas with small population size average cost and standard deviation increases. Based on the simulation result it is concluded that n=100 gives minimum generation cost.

Table 9: Effect of G0 on 54 units System (case 4, 20 trials)

Sr.No	G 0	Min cost ($/hr)	Max cost ($/hr)	Avg cost ($/hr)	SD
1.	1	22432.2510	22432.3347	22432.2928	0.0418
2.	50	22432.5305	22432.5980	22432.5642	0.0337
3.	100	22432.4986	22432.8893	22432.6939	0.1953
4.	150	22432.8355	22433.0643	22432.9499	0.1143
5.	200	22432.7453	22433.2283	22432.9868	0.2414

Table 9 shows the effect of G 0 on the performance of hybrid PSOGSA algorithm. G 0 was varied from 1 to 200 with a step increase of 50. G₀=1 gives minimum generation cost. Increase in G₀ beyond this value does not produce any significant improvement rather it increases standard deviation.

After a numerous careful experimentation the following values of PSOGSA parameters for all cases have been used.

n=100, α=10, G 0 =1, C1=2.0, C2=1.5.

Comparative Study

A) Solution Quality

As seen in the Table 1, 4 and 5 the minimum cost achieved by PSOGSA approach is 15442.3930$/hr, 62456.63309$/hr, 22432.2510$/hr for test case I, III and IV. The minimum cost obtained for the test case II is listed in Table 2, 3 and the results are very close to the recent reported techniques. Over 20 repeated trials PSOGSA approach produce small standard deviation of evaluation values in all the test cases. Table 9, 11 and 12 shows that then average cost obtained by PSOGSA approach for the test case I, III and IV is less than the reported average cost of other methods. It is observed that PSOGSA provides better results as compared to other existing techniques.

Table 10: Comparison of convergence results for 6 unit System

Method	Generation Cost ($/hr)			S.D
Method	Max	Min	Avg.	S.D
PSO	15492	15450	15454	0.0002
GA	15542	15459	15469	0.0570
NPSO-LRS	NA	15450	15450.5	NA
ABF-NM	NA	15443.8164	15446.95383	2.58223
DE	NA	15449.766	15449.777	NA
SOH-PSO	15609.64	15446.02	15497.35	NA
HHS	15453	15449	15450	0.0420
BBO	15443.096	15443.096	15443.096	NA
Hybrid SI-based HS	NA	15442.8423	15446.7142	1.8275
PSOGSA	15442.3962	15442.3930	15442.39423	0.0007

Table 11: Comparison of convergence result for 20 unit system

Method	Generation Cost($/hr)
Method	Min	Max	Avg
λ iteration	62456.6391	NA	NA
Hopfield model	62456.6341	NA	NA
BBO	62456.7926	NA	NA
QGSO	62456.6330	62456.63337	62456.6331
GAMS	62456.633	NA	NA
PSOGSA	625456.63309	62456.63310	62456.63311

Table 12: Comparison of convergence result for 54 unit system

Method	Generation Cost($/hr)
Method	Min	Max	Avg
DE	25237	NA	NA
PSO	23625	NA	NA
ALHN	23368	NA	NA
PSOGSA	22432.2510	22432.3347	22432.2928

B) Computational effciency

The statistical analysis in terms of minimum cost and average computational time is presented in Table 13 for test case I, III and IV. For repeated 20 trials minimum cost and average computational time is less and better than the mentioned methods. The results obtained are compared with the recent reported methods and shows the efficiency of algorithm.

Table 13: Comparison of Computational Efficiency

Test Case	Method	Min cost($/hr)	Time /Iter (sec)
6 unit system	PSO	15450	14.89
	GA	15459	41.58
	NPSO-LRS	15450	NA
	ABF-NM	15443.8164	NA
	DE	15449.766	0.0335
	SOH-PSO	15446.02	0.0633
	HHS	15449	0.14
	BBO	15443.096	0.0325
	Hybrid SI-based HS	15442.8423	0.9481
	PSOGSA	15442.3930	0.0420
20 unit system	λ iteration	62456.6391	0.033757
	Hopfield model	62456.6341	0.006355
	BBO	62456.7926	0.29282
	QGSO	62456.6330	NA
	GAMS	62456.633	NA
	PSOGSA	625456.63309	0.0497
54 unit system	DE	25237	282.4
	PSO	23625	136.4
	ALHN	23368	1.65
	PSOGSA	22432.2510	0.0416

C) Robustness

The search capability of heuristic algorithm can not be analyzed with a single trial because of its randomness. Therefore many trials are required with different initializations. Table 10, 11, 12 shows the minimum cost, maximum cost, average cost over 20 trials for 6 unit with RRL and POZ, 20 unit with losses and 54 unit system. The results show that PSOGSA is more consitent than other reported method as it provides lower average cost while satisfying the different constraints of the various test cases.

VI. Conclusion

In this paper hybrid PSOGSA algorithm based on the abilities of PSO and GSA is successfully employed to solve ELD problem. Here αci is used to accelerate the search space and gbest to exploit the best solution so far. The hybrid PSOGSA approach has been tested on four different standard test systems out of which first case is modeled using non linear characteristics like ramp rate limits and prohibited zone. A comparative study is carried out with the recent reported methods. From the results obtained it is seen that the PSOGSA approach affirms the effective high quality solution for ELD problem. The PSOGSA approach has the convergence speed faster than PSO and GSA. In future the algorithm can be use effectively to solve smooth and non- smooth constraint and complex ELD problem.

Acknowledgments

Список литературы Economic Load Dispatch by Hybrid Swarm Intelligence Based Gravitational Search Algorithm

Wood A.J., Wollenberg B.F., Power Generation Operation and Control, New York: Wiley, 1984.
Walter D.C., Sheble G.B., Genetic Algorithm Solution of Economic Load Dispatch with Valve Point Loading, IEEE Transcations on Power System, 1993 (8), 1325~1332.
Wang, Shahidepour S.M., Effects of Ramp Rate Limits on Unit Commitment and Economic Dispatch, IEEE transcations on Power System, 1993, 8(3):1341~1350.
Oreo S.O., Irving M.R., Economic Dispatch of Generators with Prohibited Opertaing Zones:A Genetic Algorithm Approach,IEE Proceedings, Generation, Transmission and Distribution, 1996,143(6).
Chen C.L., and Wang S.C., Branch and bound scheduling for thermal generating units, IEEE Trans. On Energy Conversion, 1993, 8(2):184~189.
K.Y. Lee, et al., Fuel cost minimization for both real and reactive power dispatches, IEE Proc. C, Gener. Trsns. & distr., 1984, 131(3): 85~93.
Shoults R.R., A Dynamic Programming Based Method for Developing Dispatch Curves when Incremental Heat Rate Curves Are Non-Monotonically Increasing, IEEE Transcations on Power System, 1986,1,10~16.
Gaing Z.L., Particle Swarm Optimization to Solving the Economic Dispatch Considering the Generator Constraints, IEEE Trans. On power systems, 2003,18(3):1187~1195.
Sinha N., Chakrabarti R. and Chattopadhyay P.K., Evolutionary Programming Techniques for Economic Load Dispatch, IEEE Transcations on Evolutionary Computation, 2003,20(1):83~94.
Noman Nasimul, Iba Hitoshi, Differential evolution for economic load dispatch problems, Electric Power Systems Research, 2008, 78:1322~1331.
Ching-Tzong S., Chien-Tung L.,New approach with a Hopfield modeling framework to economic dispatch, IEEE Trans. Power Syst., 2000,15(2):541~545.
Immanuel Selvakumar A., Thanushkodi K., A New Particle Swarm Optimization Solution to Nonconvex Economic Dispatch Problems, IEEE Trans. Power Syst., 2007, 22(1): 42~ 51.
Chaturvedi K.T., Pandit M., Srivastava L.,Self-OrganizingHierarchical Particle Swarm Optimization for Non-Convex Economic Dispatch, IEEE Trans. Power Syst., 2008, 23(3): 1079~1087.
Panigrahi B.K. and Pandi V.R., Bacterial foraging optimization nelder mead hybrid algorithm for economic load dispatch, IET Gener. Transm. Distrib., 2008, 2(4): 556~565.
Bhattacharya A., Chattopadhyay P.K., Biogeography Based optimization for different economic load dispatch problems, IEEE Trans. Power Syst., 2010,25(2):1064~1077.
Moradi-Dalvand M., Mohammadi-Ivatloo B., Najafi A., Rabiee A., Continuous quick group search optimizer for solving non-convex economic dispatch problems, electric power system research, 2012, 93: 93~105.
Biswas A., Dasgupta S., Panigrahi B.K., Pandi V.R., Das S., Abraham A., Badr Y., Economic load dispatch using a chemotactic differential evolution algorithm, Hybrid Artificial Intelligence Systems, 2009,5572, 252~260.
Pandi V.R., Panigrahi B.K., Bansal R.C., Das S., Mohapatra A., Economic Load Dispatch Using Hybrid Swarm Intelligence Based Harmony Search Algorithm, Electric Power Components and Systems, 2011,39(8): 751~767.
Xin-She Yang, Seyyed Soheil Sadat Hosseinib, Amir Hossein Gandomic, Firefly Algorithm for solving non-convex economic dispatch problems with valve loading effect, Applied Soft Computing, 2012,12, 1180~1186.
Mirjalili S, Mohd Hashim S Z, A new Hybrid PSOGSA Algorithim for Function Optimization, IEEE International Conference on Computer Information and application (ICCIA 2010), China , 2010, 374~ 377.
Ioannis G., Damousis, Anastasios G. Bakirtzis and Petros S. Dokopoulos, Network-Constrained Economic Dispatch Using Real-Coded Genetic Algorithm. IEEE Trans on power system, 2003, 18(1):198~204.
Dixit Gaurav Prasad, Dubey Hari Mohan, Pandit Manjree, Panigrahi B.K., Economic Load Dispatch using Artificial Bee Colony Optimization. International Journal of Advanced in Electronics Engineering. 2011, 129~124.
Vishwakarma Kamlesh Kumar, Dubey Hari Mohan, Pandit Manjaree, Panigrahi B.K., Simulated annealing approach for solving economic load dispatch problems with valve point loading effects, International Journal of Engineering Science and Technology, 2012, 4(4): 60~72.
Bisen Devendra, Dubey Hari Mohan, Pandit Manjaree and Panigrahi B. K., Solution of Large Scale Economic Load Dispatch Problem using Quadratic Programming and GAMS: A Comparative Analysis, Journal of Information and Computing Science(jic.org.uk), 2012,7(3): 200~211.
Dieu V.N., Schegner P., Real Power Dispatch on Large Scale Power Systems by Augmented Lagrange Hopfield Network, International Journal of Energy Optimization and Engineering, 2012,1(1):19~38.

Еще

Статья научная