Единственность решения задачи синтеза двухзвенного ступенчатого трансформатора волнового сопротивления с чебышевской частотной характеристикой

Эквивалентная схема волноводного тракта, содержащего двухзвенный ступенчатый трансформатор волнового сопротивления (ТВС), изображена на рис. 1. Здесь участки 0 и 3 с волновыми сопротивлениями z ₀, z ₃ соответствуют согласуемым отрезкам линии передачи ( z₀ ^ z 3 ) ; участки 1 и 2 представляют собой звенья трансформатора, имеющие одинаковую длину l . Решение задачи синтеза ТВС сводится к определению параметров трансформатора l , z ₁, z ₂ при заданных значениях волновых сопротивлений согласуемых отрезков линии передачи z ₀, z ₃, а также ширины полосы согласования или максимального значения рабочего затухания в полосе согласования.

Матрица передачи ТВС A [1], связывающая комплексные амплитуды суммарных напряжений U ₁, U ₂ и токов I ₁, I ₂ на его входе и выходе

UU

¹ = A 2 ,

I Л ^J 1 1 2 ^J

При записи (1) предполагается, что на отрезках

1 и 2, образующих ТВС, постоянная распро-

странения волны у имеет одинаковые значения. Тем самым, элементы матрицы A имеют вид:

A11 = cos2 (Уl)-— sin2 (уl),(2)

z ₂

A12 = i (Z1 + Z2) cos (У l) sin (У l),(3)

A21 = i I — + — J cos (Уl) sin (Уl),(4)

I ^z 1 ^z 2 J

A22 = cos2 (уl)-— sin2 (уl).(5)

z ₁

Рабочее затухание трансформатора L определяется как отношение мощностей прямых волн напряжения на его входе и выходе. Параметр L

выражается через элементы матрицы передачи ТВС A следующим образом [1]:

L = ¹ z 0

⁴ z 3

A11 +   A12 + z1 A21 + z2

равна произведению матриц передачи звеньев

A ⁽ j ) ( j = 1,2), A = A ^{( 1 )} A ^{( 2 )} , где

^

A

⁽ j )

^ cos ( у l )     iz j sin ( у l p

i

— sin ( у l )    cos ( у l )

v zj                           ,

( j = 1,2).

0   12   3

0------ z0		Z1	-			23	—0
				Z'l
			>k
Рис. 1		I		I

D 0 = JI q ^{+ 2 +} —

⁴1 q

Исходя из соотношений (2)—(6) можно представить рабочее затухание трансформатора в виде многочлена второго порядка по степеням cos² ( у l )

L = £ D m cos² m ( у l ) .                       (7)

m = 0

Коэффициенты D m ( m = 0,2 ) определяются равенствами

Рис. 2

D

1 = 4

+

( я                 я z2     z0 z3    z2    z0 z3   9 z0 z3

----------+ я +----------+ я + 2----------

( z 0 z 3      z 2 ²      z 0 z 3      z 2        ^z 1 z 2

2 zZ. - 2 z 0 z 2 - 2 z i z ! - 2 q - 2 z ₀ z ₃      z ₁ z ₃      z ₀ z ₂          q

Z Dm

m = 0

1 f z 3 + 2 + z 0L 1 f S + S T, (10)

⁴1 z 0        z 3 J   ⁴ lv ^z 0   V ^z 3 J

где q = zF. z12z3

Выражение (7) задает частотную характеристику ТВС.

Согласно определению рабочего затухания трансформатора, а также формуле (6), параметр L является действительной величиной. Поэтому соотношения (7)–(11) справедливы только при условии отсутствия затухания на любом из участков волноводного тракта, изображенного на рис. 1. В этом случае мнимые части волновых сопротивлений звеньев z ₁ , z ₂, а также постоянной распространения волны у равны нулю.

Если волновые сопротивления звеньев трансформатора и согласуемых отрезков линии передачи не зависят от частоты, то можно подобрать параметры z ₁ и z ₂ таким образом, что многочлен (7) будет иметь вид

распространения волны у пропорциональна частоте. Например, для основной волны коаксиальной линии передачи справедливо соотношение

Y = к ^/Бц, (13)

где Б и ц — относительные диэлектрическая и магнитная проницаемости заполнения; к = to/ c — волновое число свободного пространства; to — круговая частота колебаний; c – скорость света в вакууме. Постоянная распространения основной волны полосковой линии передачи с высокой степенью точности также определяется равенством (13), в котором б и ц следует рассматривать как проницаемости подложки.

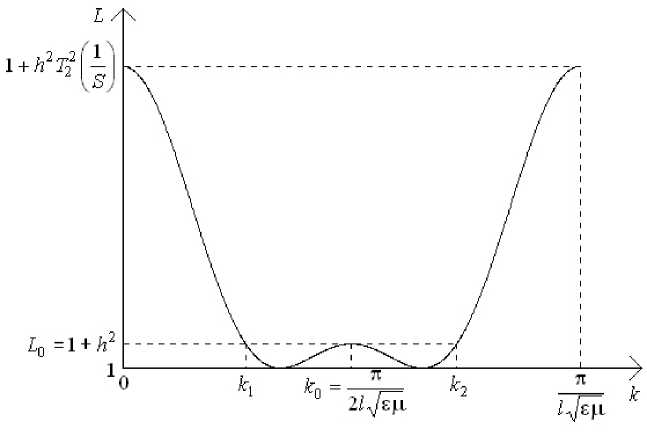
Частотная характеристика двухзвенного ступенчатого чебышевского ТВС приведена на рис. 2. Полосе согласования трансформатора соответствует диапазон значений волнового числа ( к 1 <  к <  к 2 ) , на границах которого, как и на средней частоте, рабочее затухание принимает значение L 0 = 1 + h ².

Тем самым, амплитудный множитель h в соотношении (12) определяется максимальным значением рабочего затухания в полосе согласования

h = V L 0 ^{- 1}

L = 1 + h ² T 2

cos ( у l ) S

Здесь T ₂( x ) – многочлен Чебышева 1-го рода 2-го порядка; величины h и S называются, соответственно, амплитудным и масштабным мно-

жителями.

Будем предполагать, что в волноводном тракте отсутствует дисперсия. При этом постоянная

Из рис. 2 и формулы (12) следуют равенства

cos

( к ТБц l )

= S ,

cos

( к 2 д/Бц l )

= ^- S ,

на

основании

которых получаем

cos

( к 1 ТБц l )

-

cos

( к 2 ТБц l )

f к + k₂ 1— . f k ₂ - k i

= 2sin ¹----² л/БЦ l sin 2----¹

I 2 J ( 2

д/БЦ 1 1 = 2 s .

Среднее значение волнового числа в полосе согласования

к₀ = kUkL =  ”  = • ^L.           (15)

2       2l д/бц д/бц Л -

Здесь Ло — соответствующее значение длины волны в линии передачи. Поэтому

либо получить обратное соотношение

5 = V2

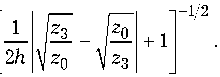
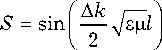
где A k = fe> - к * . Таким образом, масштабный множитель S определяется шириной полосы согласования трансформатора A к . Из равенства (15) также следует, что на средней частоте полосы согласования длина звена трансформатора l равна четверти длины волны в линии передачи Л - .

Приравнивая коэффициенты при одинаковых степенях cos² ( у l ) в выражениях (7), (12) получаем систему уравнений:

D₀ = 1 + h ², (17)

Тем самым, дальнейшие наши рассуждения будут справедливы для обоих вариантов постановки задачи синтеза ТВС.

На основании (8), (17) можно получить ква-

дратное уравнение относительно величины q q ² - 2 ( 1 + 2 h ² ) q + 1 = 0.

Его решения:

q₁₂ = 1 + 2 h ² ± 2 h V1 + h ²

1 + h ² ± h ) .

При помощи формулы (11) можно выразить одно из неизвестных волновых сопротивлений звеньев трансформатора через другое

D 1 =

4 h ²

S ^{2 ,}

D

4 h ²

²     5 ⁴ .

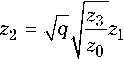
В качестве неизвестных в этих уравнениях выступают волновые сопротивления звеньев трансформатора z ₁ , z ₂. Если задача синтеза ТВС решается при заданной ширине полосы согласования A к , то из (16) можно определить масштабный множитель S . В этом случае третьей неизвестной в системе (17)–(19) является амплитудный множитель h . Другой вариант постановки задачи синтеза ТВС предполагает известным максимальное значение рабочего затухания в полосе согласования L ₀. При этом, в соответствии с (14), амплитудный множитель h является исходным параметром задачи синтеза, а масштабный множитель S – неизвестной величиной.

Согласно (10), сумма коэффициентов D m , ( m = = 0,2) определяется только известными волновыми сопротивлениями согласуемых отрезков линии передачи z ₀, z ₃. На основании (10), (17)– (19) имеем

2                                2 ²

V d = 1 + h ² f А -1) = ¹1 z 3 + z - I .

£ 0 m V 5 ^{2 J 4} W z о z^z3)

Данная формула позволяет выразить амплитудный множитель через масштабный

С учетом соотношений (9), (22) можно сти уравнение (18) к виду azi - 2bzi + c = 0.

Здесь

приве-

b =

z ₀ z ₃

^q z 0 ²

2 q

q )²

z ₀ z ₀ z ₃

z 0 z 3     z 0

,

q

-

₈ h 2 _, S ²

² z 2

c = ^z 0 ^z 3 ⁺ - ⁺ T ^z 0 ^^z0 ^z3 =

I-------- , ^z 0

V ^z 0 ^z 3 +“/=

V v q

. (26)

В

результате имеем

z i = a ( ь ±^a^ ,

где

A = b ² - ac = ( b - Oo e ) ( b + Oo e ) .

В соответствии с (24), (26)

f ac = 2 +

V

Выразим все величины, присутствующие в (25), (29) через амплитудный и масштабный множители h , S . Согласно (8), (17)

^{1 5 2}   4 - / z -

2 2 - 5 ² \ z o    \:₃

1 S ²

2 2 - 5 ²

sign

^z 3 ^{- z} 0 _ч T z O z s ,

f S - S I, u ^z 0 z^z3 )

---- = ² ( 1 + ² h ² ) ^- q 1,2 . q 1,2                           ^,

Подстановка (21) дает

—1- = 1 + 2 h ² + 2 h 71 + hh¹

q 1,2

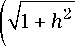
т h ) ².

Введем обозначения:

а=. ^ в=.=1.

V z o        Z^z3 ^а

С учетом этого, равенство (20) можно записать

b +

V ac =

= 4

1 +

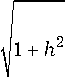
+ h ²

( 2 - S ² ) 2

S ⁴

+ h ⁴

( ² -

S ² ) ²

-

в виде квадратного уравнения относительно а или в

а

(

- а sign

в2 + в sign

^z 3

- ^z 0

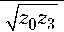
^z 3 ^{- z} 0

. v zz,

2 h

2 h

- S ²

S ²

-1 = 0,

-

h ²²

- S

S ²

- S ²

S ²

-1 = 0.

Положительные решения этих уравнений имеют вид:

а

h ²

( 2 - S ² ) 2

S ⁴

+1 + sign

( z3

-

^z 0

z ₀ z ₃

h 2- S -, (31)

S ²

легко убедиться в справедливости неравенства

b +

v ac > 0.

Если волновые сопротивления согласуемых

h ²

( 2 - S ² ) 2

S ⁴

+1 - sign

^z 3 ^{- z} 0

h ²

-

S ²

отрезков линии передачи удовлетворяют условию Z 3 >  Z 0 , то, в соответствии с (35) b i <  -Ja i c , ^b 2 = V ^c T .

При этом, согласно (28), (36) A i < 0, A 2 = 0.

В случае z 3 <  Z 0 имеем b = a i c , b 2 <  ^Ja 2 C 2 , A_i = 0, A₂< 0.

^z 0 ^z 3 J

S ²

. (32)

Таким образом, вне зависимости от того, как

Подставляя выражения (21), (30)–(32) (29) находим

в

(25),

соотносятся величины z ₀, z ₃, одно из решений (27) уравнений (23) является действительным

положительным

b = 2 + 2л/1 + h ² h^г

( 2 - S ² ) 2

+ 2 sign

z 3

-

z 0

z ₀ z ₃

h

S ⁴

2 2 - S ²

+1 +

2 b ^z i = — a

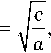
S ²

-

4 h ²²

-

S ²

оставшиеся два решения имеют отличные от

ac = 2+ 2^1 + 2 ² a h

2 ( ² - ^{S 2} ) ²

± 2sign

или

^z 3

-

^z 0

z ₀ z ₃

h

2 2- S

S ⁴

S 2    ,

^b 1,2 = -J ^a 1,2 ^c 1,2 ^{- 4 h 2}

2 - S ²

S ²

1 ± sign

S ^2,

нуля мнимые части, являясь комплексно сопря-

женными.

Обратимся теперь к определениям, связыва-

ющим волновое сопротивление z и постоянную

распространения волны у с погонными параме-

^z 3

"

Из (33), (34) также следует, что

b + V ac =

= 4

-

-

z ₀

z ₀ z ₃

. (35)

трами линии передачи [2]:

_z 2 = R n + i to L П = R П G П ^{+ ю} 2 L П С П G п + i to С п G П + to² С П

. L n G n - R n C n + i to -^Пу^П--2^2^, G П + ^{to C} П

У = ^- i 4 ( R n ⁺ i ^to L n ) ( G n ⁺ i ^{to С} П ) =

= ^- i\ ( R П G П

^{- to} 2 L n ^C n )

+ i ^{to (} L n G n ⁺ R П ^C n ) .

1 + V1 + h ² h

2 ( 2 - ^S 2 ) ²

S ⁴

+1 -

_h 2 2

-

S ²

S ²

.

Записав данное соотношение в виде

Здесь L _П и C _П – погонные индуктивность и емкость; R _П – погонное сопротивление проводников линии передачи; G _П – погонная проводимость изолятора, разделяющего проводники. Как следует из (38), для того, чтобы мнимая часть величины z ² была отлична от нуля, необходимо наличие потерь в линии передачи R n * 0 и (или) G n * 0. При этом, согласно (39) 0 < arg Г ( i у ) ² "1 < п.

Отсюда получаем

0 < arg ( i y ) < П,

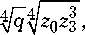
или

n

< arg ( y ) < 0.

Тем самым, комплексным значениям величин z ², z соответствует комплексная постоянная распространения y. Как было отмечено выше, в этом случае неуместно представление рабочего затухания трансформатора в виде многочлена (7) с коэффициентами, задаваемыми формулами (8)–(10). Таким образом, как бы ни соотносились

волновые сопротивления согласуемых отрезков

линии передачи z ₀ и z ₃ , существует единственное решение ( z ₁, z ₂) задачи синтеза двухзвенного ступенчатого ТВС с чебышевской частотной характеристикой.

На основании (24), (26), (37) имеем

Л zi =

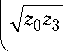
Л

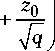
_v V z G z a

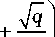
z 0 J

где

q = 1 + 2h ² - sign

z   2 h U + h ³ =

TiT h ²

- sign

₄ V z 0 z 3 ,

( z3

- ^z 0

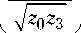
h

Легко убедиться в том, что величины z ₁ и z ₂ удовлетворяют условию

z 1 z 2 = ^z 0 ^z 3 .

Формулы (40), (41) отличаются от аналогичных соотношений, полученных в [1], множителем

или z1 =     z 0

q

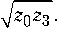
Принимая во внимание соотношения (21), (22) получаем следующие выражения для волновых сопротивлений звеньев трансформатора

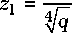
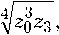
^z 3 ^{- z} 0

sign ³----⁰ .

I V ^z 0 ^z 3 J

Следует также отметить, что использованный в [1] подход оставляет открытым вопрос о существовании иных решений задачи синтеза двухзвенного ступенчатого ТВС с чебышевской частотной характеристикой.

Ñïèñîê ëèòåðàòóðû

Uniqueness of solution of problem of synthesis of wave impedance two-link stepped transformer with Chebyshev frequency characteristic

A.S. Aref’ev