Effect of electron-phonon interaction on transport properties in TmxMn1-xS

Introduction. To create an element microelectronic base for operation under extreme conditions in a wide temperature range (for example, in small spacecraft and nanosatellites), it is necessary to use new principles of recording, reading and processing information. Semiconductor electronics have limitations in operation both at low and high temperatures. Using the spin degrees of freedom of an electron expands the temperature range and makes it possible to create a nanoscale element base in microelectronics. The principle of recording information is based on the change in resistance in a magnetic field and dielectric constant in a magnetic field.

Magnetoresistance is being actively studied in inhomogeneous semiconductors with phase separation [1; 2], coexistence of crystallographic phases [3–7] and ferrons [8–9]. In addition to charge and spin, it is necessary to take into account the orbital degrees of freedom of electrons and the effect of orbital angular momentum of electrons on the kinetic properties in semiconductors [10–15] and the formation of electronic phase transitions [16–19]. In a magnetic field, the energy of an orbital polaron depends on the phase of an electron [12]. As a result, a magnetoresistive effect is possible in the absence of static lattice deformations. The exchange interaction of localized and delocalized electrons leads to anomalies in the temperature dependence of electrical resistivity and to the formation of magnetoresistance, which is the most apparent in compounds with 4f rare earth elements [20–23]. The spin-orbit interaction at the interface in semiconductors leads to a significant increase in the value of the magnetoresistance in the paramagnetic region. There is another mechanism of magnetoresistive effects at high temperatures up to T = 600 K; if we take into account the orbital degree of freedom of an electron, as a result of ferromagnetic ordering of orbitals, the electronic structure is rearranged and quasi-cracking is induced on the Fermi surface in a magnetic field [24–25].

Magnetoresistive effects depend on the type of current carriers, lattice or spin polarons, orbitrons. For this, it is necessary to study the structural characteristics and phonon modes of lattice vibrations. Electron or hole doping in manganese sulfides leads to degeneracy of 3d orbitals, which can be removed due to the Jahn–Teller interaction, or with the formation of orbital or charge ordering. Transport characteristics depend on the type of a magnetic structure, which, in turn, can vary significantly from the interaction of the spin and electron subsystems with the elastic lattice [26–35].

Charge ordering is observed in transition metal oxides and attracts interest due to the effect of giant magnetoresistance in manganites in AMnO3(A = Y; P r; Nd:::) [36]. Charge disproportion is a common property for the family of perovskites AMeO3(A = P r; Nd:::; Me = Mn; Co; Ni) and is closely related to a sharp increase in conductivity below a certain critical temperature. In manganites, upon heating the orbital ordering first disappears; at a higher temperature the cooperative ordering of the Jahn–Teller distortions of the octahedron disappears as well [37]. In AMnO3(A = La; P r; Nd:::) compounds, a gap is formed in the spectrum of single-particle electronic excitations, and the resistance is described by the polaron type of conductivity between these temperatures [37]. The activation energy is in the range 0.3eV < Ea < 1.2eV and the conductivity is of the semiconductor type. The spectral weight of optical conductivity shifts to low energies upon heating [38], and local distortions of the octahedron are retained in the lattice without changing the angle of inclination of the octahedron in the cluster. An increase in the resistance in manganites below the Jahn–Teller temperature is explained by the disproportion of manganese ions [37].

The replacement of manganese ions in manganese sulfide with ions of variable valence will lead to degeneracy of electronic states, which can be removed as a result of the Jahn -Teller interaction. It is the reason for the strong electron-phonon interaction and it will influence the resistive characteristics of the material.

The aim of this work is to establish sample deformations and relate them to the anomalies of the transport properties, which can be explained in the model of the interaction of current carriers with the vibration modes of an octahedron.

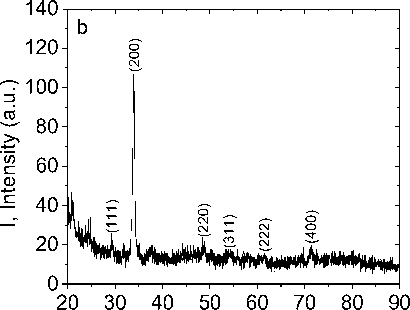
Structure and IR spectra. The solid solutions of Tm x Mn 1-x S were obtained by melting and crystallization from a melt of polycrystalline manganese sulfide and polycrystalline thulium monosulfide [39–40]. The X-ray structural analysis of Tm x Mn 1-x S (0,0 ≤ Х ≤ 0,15) sulfides was carried out on the DRON-3 installation at CuKα radiation at the temperature of 300 K after obtaining them and measuring their transport properties. X-ray diffraction patterns correspond to the face-centered cubic lattice of the NaCl type (Fig. 1). An increase in the background of the X-ray pattern is associated with incoherent scattering by local lattice deformations. With an increase in the degree of cationic substitution (X), the unit cell parameter а increases linearly from a = 0.55 to 0.64 nm.

го

w с ф

a

HWMnVW*

vwUmWWW^wW**1

20  30  40  50  60  70  80  90

2 0, degree

<|А**М<мЦ**<

2 0, degree

Рис. 1. Рентгеновская дифрактограмма образцов Tm0.1Mn0.9S (a) и Tm0.15Mn0.85S (b) при комнатной температуре

Fig. 1. X-ray diffraction pattern of the Tm 0.1 Mn 0.9 S ( a ) and Tm 0.15 Mn 0.85 S ( b ) samples at room temperature

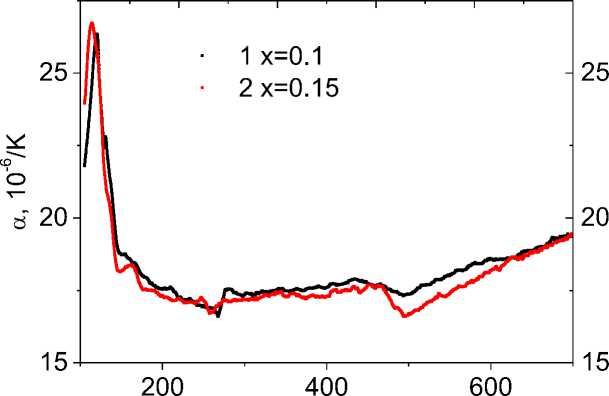
The influence of the replacement of thulium ions (which have a larger ionic radius in comparison with manganese ions) on the structural characteristics, in particular, the change in volume, is determined by the temperature from the coefficient of thermal expansion, the temperature dependences of which are shown in Fig. 2. The change in sample volume relative to the temperature was measured on the DIL-402C dilatometer. For all compositions, minima are observed in the range 260–270 K, and at high temperatures of 485–495 K the value of the minima increases with increasing concentration. At these temperatures, the growth of the sample volume slows down. A decrease in the sample volume, as compared to the ∆V/V(T) asymptotic continuation, is associated with depinning of lattice polarons above the Debye temperature TD = 250 K. Small minima in α(Т) in the range 355–370 K are caused by lattice deformation as well. Lattice deformation at T = 490 K is caused by the electron compressibility of the sample as a result of electron localization.

T, K

Рис. 2. Температурная зависимость коэффициента термического расширения α(Т) для образцов Tm x Mn 1-x S при x= 0.1 ( 1 ), 0.15 ( 2 )

Fig. 2. The temperature dependence of coefficient of thermal expansion α(Т) for the Tm x Mn 1-x S samples with x= 0.1

( 1 ), 0.15 ( 2 )

The model of lattice polarons is confirmed by IR spectra recorded in the frequency range of 450 cm-1 – 7500 cm-1 and the temperatures of 80–500 K on the FSM2202 Fourier spectrometer. In this frequency range, two frequencies were found, the intensity of which disappears upon heating in Fig. 3. For three compositions, the absorption spectral line in the vicinity of the frequency ω1 = 3116 cm-1 (Fig. 4) disappears in the temperature range 240–270 K. A lattice polaron below the Debye temperature TD = 255 K for manganese sulfide is pinned at anion vacancies. The IR mode at the frequency ω1 = 3116 cm-1 corresponds to the energy of the transition of an electron from a localized polaron to a vacancy.

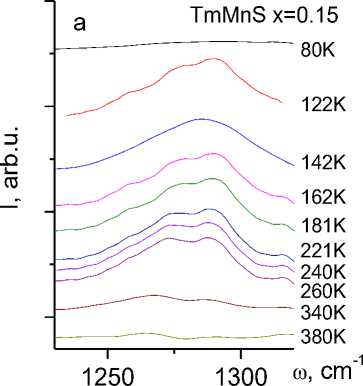
Рис. 3. ИК спектры для образцов Tm x Mn 1-x S при x=0.15 ( а , b )

b        TmMnS x=0.15

142K

162K

181K

221K

240K

260K

280K

3050  3100  3150 ω , cm

Fig. 3. IR spectra for the Tm x Mn 1-x S samples with x=0.15 ( а , b )

The thermal vibrations of ions, i.e. the interaction with acoustic phonons, lead to depinning of polarons and the intensity decreases in proportion to the density of acoustic phonons I ab ~ 1-AT. This function qualitatively describes the experimental results with the critical temperature of detachment of polarons from lattice defects. The absorption intensity at the frequency of 1240–1320 cm^-1 is associated with the pinning of optical polarons at the Mn-Tm interface.

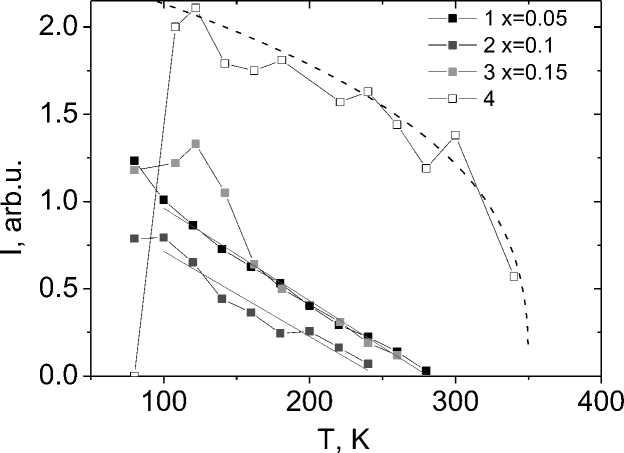
Рис. 4. Температурная зависимость интенсивности ИК спектров для образцов Tm x Mn 1-x S при x=0,05 ( 1 ), 0.1 ( 2 ), 0,15 ω=3110 cm^-1 ( 3 ), 0,15 ω=1290 cm^-1 ( 4 ). Степенная функция I = A(1–T/T c )^0.35 (пунктирная линия)

Fig. 4. The temperature dependence of the IR spectra intensity for the Tm x Mn 1-x S samples with x=0.05 ( 1 ), 0.1 ( 2 ), 0.15 ω=3110 cm^-1 ( 3 ), 0.15 ω=1290 cm^-1 ( 4 ). The power function I = A(1–T/T c )^0.35 (dotted line)

The deformation of the octahedra at the boundary of Mn-Tm clusters is described by the power dependence I=A(1–T/T c )^0.35 with the temperature Т с =350 К. As the temperature Т=500 К is approached, an increase in the absorption intensity at the border of the frequency range 450 см^-1 is discovered.

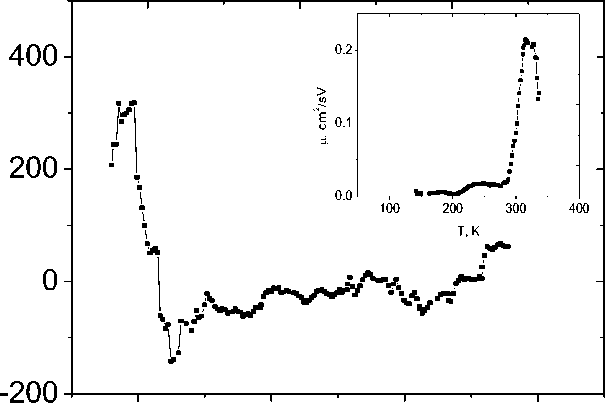
In the vicinity of the temperatures of lattice deformations and pinning of lattice polarons, the temperature coefficient of electrical resistivity 1/R dR/dT has anomalies. Fig. 5 shows the temperature dependences of resistance in the range 100–600 K. All the three compositions are characterized by an approximately twofold increase in the activation energy in the temperature range of 340–370 K from ΔE=0,3–0,4 eV to ΔE=0,6–0,8 eV. In this temperature range the sign of the Hall coefficient (Fig. 6) and accordingly the type of current carriers change from negative to positive when being heated. A change in the sign of the charge carriers is also observed below the transition temperature to the magnetically ordered state. An increase in the activation energy is associated with the shift in the chemical potential from the donor level to the acceptor level. The discrepancy between the signs of the thermal electromotive force and the Hall resistance is caused by the entrainment of electrons by acoustic phonons, which causes the positive sign of the thermal electromotive force below Т = 350 K. A similar phenomenon was observed in oxides [41].

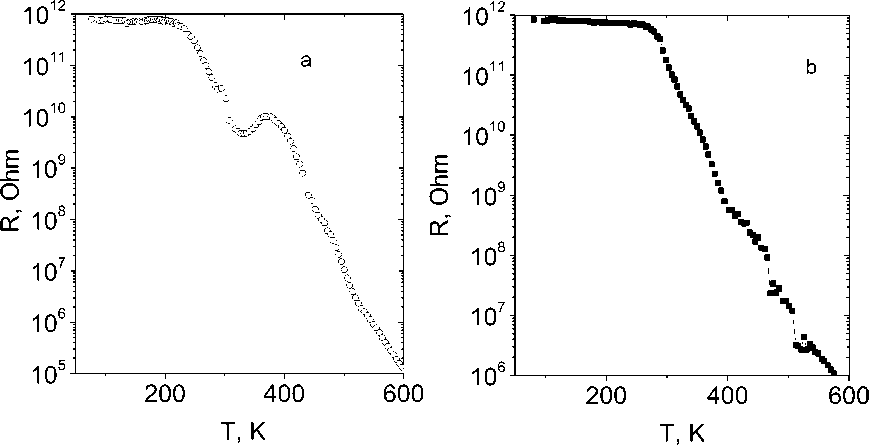
Рис. 5. Зависимость сопротивления от температуры образцов Tm x Mn 1-x S при x= 0,1 ( a ), 0,15 ( b )

Fig. 5. Resistance of the Tm x Mn 1-x S samples with x= 0.1 ( a ), 0.15 ( b ) versus temperature

The temperature of the maximum mobility of current carriers corresponds to the minimum of electrical resistance. The model that qualitatively explains the anomalies in electrical resistivity and deformation is being discussed below.

100     200     300     400

T, K

Рис. 6. Температурная зависимость коэффициента Холла, измеренного в магнитном поле H=8 kOe перпендикулярно току, образцов TmxMn1-xS при x=0,1. Вставка: температурная зависимость подвижности электронов (носителей заряда) в магнитном поле H=8 kOe для образцов TmxMn1-xS при x=0.1 в температурном диапазоне 80–400 K

Fig. 6. The temperature dependence of the Hall coefficient measured in the magnetic field H=8 kOe perpendicular to the current for the Tm x Mn 1-x S samples with x=0.1. Insert: temperature dependence of the mobility of electrons (charge carriers) in the magnetic field H=8 kOe for the Tm x Mn 1-x S samples with x=0.1 in the temperature range 80–400 K

Model . Let us consider the charge transfer due to one-electron hopping over the sites of the anion lattice, under the assumption that the Fermi level lies between the bonding and antibonding orbitals. Both single-particle electronic excitations and two-particle electron + hole contribute to the thermal electromotive force, imitating the movement of a covalent bond, which can be described by two-electron excitations along the crystal lattice and symbolically represented as M +³"⁵ - S ^-2+5 — M⁺³ ^ M +³"⁵ — S " ²⁺⁵ - M ⁺³"⁵ . The effective charge transfer Hamiltonian has the following form:

h = h₀ + h + h₂

H о = Z ⁽ ^ d ^- p ) c i ci ⁺ Z ⁽ p - ^£ o ) a a , a ,- ^- Z kj ( ^a + a 2, j + a 1, a + , j ) - i                                          a , i                                             i , j

• - Z t 2,ik ( c i + a a X p,k c k ⁺ c i a^a e ,k c k ) ⁺ Z ^A i ( al ,i a 1, i - a 2 , i a 2,i ) ⁺ Z Un a 1,i n a 2, j i , k , a , в                                                                 i , a , в                                          a , i , j

H, = 7 <2,. \a, c ⁺ + ate.) (b ⁺ + b 1             , c + + at, c, ) ( p⁺ + p ) >

• 1     / j |o 1, q у ^1, i*^i ^1, i*^i J - У - q qq /    g 2, kq \  2, k k      2, k k )\^p - q ^p q /I

i , k , q

^H 2 = Z ( ^ 1 q ^b q ^b q ⁺ ^ 2 q P^ q P q )

q

Here E d,a is an electronic level in 3 d atoms of metal and sulfur ions; t i is an integral of the electron hopping over the p x ,  P y   orbitals; the third term describes the movement of the

V ₂, ( а , в = x , y , z ) covalent bond in a simple cubic lattice, and the summation is carried out over the

Me – S, c ⁺ bonds; a are the operators of creation and annihilation of electrons on metal and sulfur ions, respectively; Δ is the parameter of the crystal splitting of the orbital triplet on the sulfur ion; g 1 and g 2 are the parameters of the interaction of the electron density at the Me – S bond with the bending ω 1 and stretching ω 2 modes of the octahedron. Let us compose a system of equations for electrons and holes taking into account the conservation of second-order operators. The corresponding equations obtained in the random phase approximation have the following form:

d

dt

a

h                             i , q

( ^ 0 - M - ^A + Un ai 1 ) ^a2i + £ t_u -₊ h Q i -+h + £ g 2 _i q c_i ( p q + p - q )

h                           , q

id ⁽ “ub - , f-fi

M - A + Un i 2 — « 1, - q n - q )( “ li b - q ) — g ^ ( 1 + n - q — n_a 1 ) c i

i d^ ( “ 1 Л ) = " ( ^£ 0 - M ^-A + ^Un“ 2 + « 1 q n q )( “ 1, i b + ) + g 1, iq ( n q + n_a 1 ) с , d- ( “ 2,i P - q ) = - ( ^ 0 - M ^-A + Un_a 1 - « 2, - q n - q )( “ 2- P - q ) - g 2_-q ( 1 + n - q - n “ 2 ) c ,

id ⁽ “ 2, . p q ) = -U.

M ^{- A} + Un a 1 + « 2q n q ) ( “ 2i P q ) + g 2,iq ( n p + n a 2 ) c i

i

d

dt

^{( Cb}+Wd

d ⁽ c ^M^

- M ⁺ « 1,q n q ) ( c i^bq ) - g 1,iq ( n q ⁺ ne ) “ 1, i

M ⁺ « 2, q n p ) ( c i P q ) - g 2,iq ( n p ⁺ n e ) “ 2, i

i d (cib-q ) = (Sd - M + «1,-qn-q ) (cib-q ) - g 1,iq (1 + n-q - ne ) “1,i i d-t (C,p-q ) = (^d - M + «2,-qn-q ) (C^-q ) - g2,iq (1 + n-p - ne ) “2,i

where n ,n ,n ,n are the average occupation numbers of phonons, due to the symmetry of the optical phonon modes with respect to the center of zone n_?= nq, n_p = np are determined as П p = (exp (h« 2 / kT -1))  . The filling parameters of the zones nc, naX 2 determine the position of the chemical potential.

The Green's functions for G?" =((a„b|aG )) holes and Gcb„a =((e.bA la +.  ) polarons have the k          а,к a,k                     k+q         k k +q   a,k following form:

( « + a _aa ) G " + 8 1 ( k ) G ^ - g kq ( G^ + Gt " ) = 0

-8 1 ( k ) G " + ( « + a ) G k - g kq ( G ^ + G ^) = 1

g " kq ( n q ⁺ n c ) G a ^{+ G}^ ( « ^{+ 8} d ⁺ M ⁺ n q « a _A ) = ⁰

g " kq ( 1 ⁺ n q - n c ) G a ⁺ G k^ ( « ^{+ 8} d ⁺ M - n q « a , q ) = ⁰

g e kq ( n p ⁺ n c ) ^G k ⁺ G k^ ( « ^{+ 8} d ⁺ M ^{+ П}р®р_А ) = ⁰

g e kq ( 1 ⁺ n p - n c ) ^G k ⁺ G S ( « ^{+ 8} d ⁺ M - ^Пр®р_А ) = ⁰ 8 ( k ) =- 2 4 ( cos ( k_x / 2 ) • cos ( k_y /2 ) + + я ( cos ( k _z / 2 ) - cos ( k_x / 2 ) + cos ( k _z / 2 ) • cos ( k_y / 2 ) ) )

where the λ parameter describes the anisotropy of the hopping integrals in the plane and between the planes; below we use the value X = 0.25. The Green's functions of electrons for G "" = ^^ c_k|c | ^^ holes and G ^ + q = (( a _a , _k b + q c +1\ , G "^p _q = (La k , _k p _k-q| c + 11 polarons form the following system of equations:

cc            /blb+    /blb               z'i2b+

⁽ « + ⁸ d + ^M ) G k + ^g 1 kq ( G k ₊ q + G k _ q ) + ^g 2kq ( G k ₊ q + G k - q ) = 1

• -g 1kq (nq + na 1 ) Gk + (« + 80 - M - A - Una2 + nq«1q ) Gk +q =

g 1kq (1 + nq + na 1 ) ^ + (« + 80 - M-A-Una 2 - nq«1q ) Gk^ = 0

• -g2kq (np + na2 ) Gk + (^ + 80 - M + A - Una 1 + np^2q ) Gk^+pci =

• g 2kq (1 + np + na 2 ) Gk + (^ + 80 - M -A- Una 1 - np^2q ) Gk-q =

The fluctuations of the Me - 0 bonds are described by two operators of hole creation on oxygen and electron annihilation on metal ions:

d i dt

( ^ci^a + i ) = ( ^ci^a + i ) ( n a 1 ( ⁸ 0

• ^{- 8} d ^{- A)- m (} n c ⁺ n a 1 ^)- n a 2 ^{( U + 8} d ) ) - n a 2 ^ t 2i i , h 1 ( c i + h 1 ^a + i + h 1 ) ^-

• h1

  _-

'na2 E t2,i,h 1 (a2+,i+h 1 ci+h 1 ) + na2 E g 1,iq (Ь^ + Ь-q ) h1

idt^ ^a 2, k c k )    ^{( a} 2, k c k ⁾⁽ n^a 1 ^{( 8} 0    ⁸ d

• ^{-A)- m (} n c ⁺ n a 2 ^)- n a 1 ⁽ U ^{+ 8} d ) ) ⁺ n a 1 E t 2, i , h 1 ( ^a + , k + h 1 c k + h 1 ) ^- h 1

  _-

  
  

'na 1 E t2,k,h 1 (ck+h 1a2,k+h 1) + na 1 E g 2, kq ( p|+ Г - q ) h1

d

( ^a 2,i^ci ^{+ a} 2 ⁺ , i^ci )

i — bn = ^bn + 7 gAi dt q       1 q      i1

i ^d p q = « 2 p q ⁺ E g 2 1 ( ^a 2, l c l ^{+ + a} 2 ⁺ , l c l )

When composing the equations, we used the M +³"⁵ - S "²+⁵ charge conservation law, associated with the transfer of electron density from sulfur to a metal cation and the correlation effects between different orbitals were neglected. The 5 parameter determines the covalent contribution on the ion. We represent the operator of two Fermi particles in the form т_к = E Ck+_qa +_q and dk = E a + _qCk+_q • We introduce

Green's functions for one type of connections G T = ( It. T .⁺ )V G d = ( (d. I t ⁺ )), G b = ( lb. T ,⁺ )V k    kk    k    kk    k    kk

Gp = \ \P k I <) /. The system of equations has the following form:

( « - a- ) GT + n_o 2 8 2 ( k ) G d + g i k n_a 2 G = G ¹ n« 1 8 2 ( k ) G T + ( « — a idd ) G k ^T + g 2 k n a G = 0 g i k G ^{+ (} « ^- « 1 ) G i b " = ⁰ - g 2 k G d + ( « - « 2 ) G p = 0 a i T = n a 1 ( ⁸ 0 ^{- 8} d - ^A ) ^- ^ ( n c ⁺ n a 1 ) ^- n a 2 ( U ^{+ 8} d ) ^- n a 2 ' ⁸ 2 ( k )

a i, d = n a 2 ( ⁸ 0 - ⁸ d ^{+ A} ) - ^ ( n c ⁺ n a 2 ) - n a 1 ( ^{U + 8} d ) ⁺ n a 1 ' ⁸ 2 ( ^k )

8 ( k ) = - 2 1 ₂ ( cos ( k_x ) + cos ( k_y ) + cos ( k _z) )

The system of equations for the Green's functions with a different type of connections dd / / j I 7 + \ \      т d / / I j + \ \ bdbd / /1 I _7+ \ \      pd           l_7+\\i xi .cn * c

G k = \\ d _k | d _k ^ , G _k =   T _k | d _k ^ , G _k = ^ b _k | d _k ^ , G k =   p _k | d _k ^ has the following form:

( « - a_L d ) Gk + n a , 8 2 ( k ) G T d + g 2 k n a . G k" = G ² » a2 8 2 ( k ) G k d + ( ® - a„ ) G T d + g „, n a 2 G k - = 0 ( - « + « 2 ) O k p + g 2 k G k^d = 0 ( - ® + « ) G k - + g ! k G k d = 0

The chemical potential is calculated self-consistently by the numerical solution to the system of three equations:

n c = 77 EJ d « f ( « ) -Im G k C q

N k ,q J na 1 = T7 EJ d« f («) “Im Gk1q

N k ,q na 2 = T7 El d« f («) "Im Gk2q

N tr where f (to) = (exp(to/ T) + 1) . From the summation over the impulses, we can proceed to integration taking into account the seed electron density of states, or direct calculation of the sum over the electron and phonon impulses over the first Brillouin zone with a step of Δk = 0.2 over 109 points, which cannot be performed on modern computers. To work around this problem, we assume that the optical modes and the coupling function of an exciton (electron + hole) with phonons are independent on the momentum q. This is equivalent to considering interactions with long-wavelength optical vibration modes.

з

c

d

-2

e

го /1

m /1

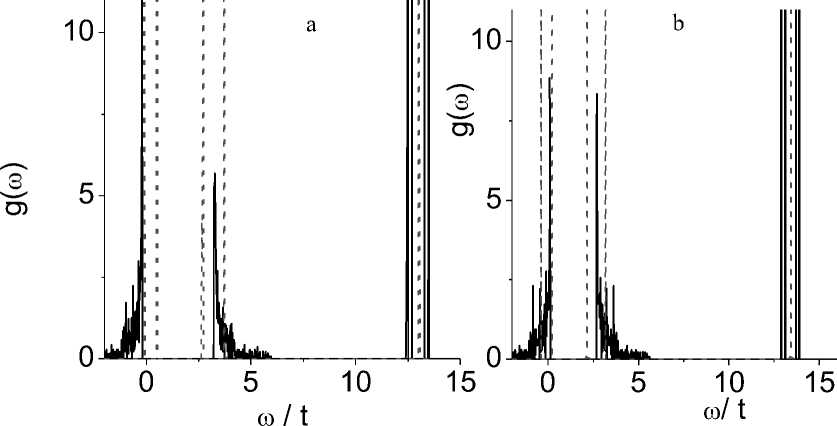
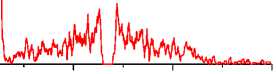
Рис. 7. Плотность состояний для одночастичных электронных возбуждений при следующих параметрах: (a) A= 1,5, U = 3, ro i = 0,25, Ю 2 = 0,4, g 1 = 0,02, g 2 = 0,3, n = 0,2, £ o - £ d = 15 и T = 0,02; ( b ) то же самое и T = 0,6; и (c) A= 1,0, g 1 = 0,6, g ₂ = 0,05, n c = 0,32, £ o - £ _d = 5 и T = 0,02. Плотность состояний для двухчастичного возбуждения (электрон+дырка) при (d) A= 1,5, U = 3, ю 1 = 0.25, ю₂ = 0.4, g 1 = 0,02, g ₂ = 0,3, n c = 0,2, £ _o - £ _d = 15 и T = 0,02

Fig. 7. Density of states for one-particle electron excitations at the following parameters: (a) ∆= 1.5, U = 3, ω 1 = 0.25, ю₂ = 0.4, g 1 = 0.02, g ₂ = 0.3, n c = 0.2, £ o - £ d = 15, and T = 0.02; (b) the same and T = 0.6; and (c) A= 1.0, g 1 = 0.6, g ₂ = 0.05, n c = 0.32, £ o - £ d = 5, and T = 0.02. The density of states for two-particle (electron + hole) excitations at (d) A= 1.5, U = 3, Ю 1 = 0.25, ш₂ = 0.4, g 1 = 0.02, g 2 = 0.3, n c = 0.2, £ o - £ d = 15, and T = 0.02

The rhombic anisotropy in (1) actually reflects the interaction of the pseudospin orbital moments of sulfur T = a_x ⁺ a_x — a + a ₂ with the crystal field, and leads to the splitting of the band into two subbands, which begin to diverge with an increase in the rhombic anisotropy parameter. In the gap area, there are two narrow polaron mini-subbands, the position of which changes depending on the electron-phonon interaction constant. One of them is located above the top of the valence band, and is formed as a result of the interaction of electrons with a flexural vibration mode. Another level lies near the bottom of the conduction band and is caused by the interaction of electrons with stretching modes of the octahedron. Localized states of the electrons on 3d metal ions are high in energy; they are shown by a number of lines in the energy range ω/t = 10 - 15 in Fig. 7 a , b . The typical behavior of the density of states for different parameters of the electron-phonon interaction is shown in Fig. 7. For small parameters g 1 << 1, g 2 << 1, polaron mini-subbands contract into narrow lines, similar to impurity states in semiconductors. Their position relative to each other and the chemical potential determines the temperature behavior of the resistance.

For phonon frequencies ω 1 /t = 0,2, ω 2 /t = 0,4 and the rhombic distortion parameter corresponding to the Jahn–Teller lattice distortions Δ/t = 1,3, it is possible to obtain different dependences of the temperature behavior of the resistance, determined by the parameters of the electron-phonon interaction and the value of the rhombic distortion of the crystal field. A decrease in the gap width with increasing temperature leads to the displacement of the top of the valence band relative to the chemical potential, and at a certain critical temperature, the chemical potential moves into the zone, which causes a sharp decrease in resistance.

Conclusions. In the solid solution Tm x Mn 1-x S, the temperatures are established at which the sample volume changes and the temperature coefficient of electrical resistance has its maximum. The temperatures of disappearance of the IR absorption spectra at certain frequencies are found. The lattice deformation is caused by the localization of electrons in the vicinity of thulium ions as a result of the electron-lattice interaction with acoustic and optical modes of lattice vibrations with decreasing temperature. The detachment of electrons induces the maximum of carrier mobility. The model of the interaction of electrons and holes with bending ω 1 and stretching ω 2 modes of an octahedron is proposed. The electronic structure and the spectrum of electronic excitations are calculated in the random phase approximation. The polaron levels in the density of states associated with flexural and tensile modes of the octahedron are found.