Effect of Rare-Earth Element Doping on Fe-Ga Alloys Properties: Tab Initio and Monte Carlo Modelling

Magnetostrictive materials are an important part of modern manufacturing technologies. Due to their volume-preserving deformation in the direction of the applied magnetic field, they are widely used in actuators, sensors and transducers. The elongation of the sample under a magnetic field or mechanical stress is a consequence of magnetoelastic coupling arising mainly from spin-orbit interaction associated with elastic distortions. The highest value of saturation magnetostriction 3/2A _s = 2630 x 10 ^{- 6} at room temperature was found in the Tb-Fe ₂ alloy [1]. However, this alloy, like the DyFe 2 alloy (3/2A s = 650 x 10 ^{- 6} ), has large magnetocrystalline anisotropy (MA), which requires strong magnetic fields to bring it to saturation. To reduce MA, Tb and Dy were added to Fe in the correct proportion, and the resulting intermetallic compound Tb ₀,₂₇ Dy ₀,₇₃ Fe ₂ (commercially known as Terfernol-D) [2] showed 3/2A _s 2000 x 10 ^{- 6} at room temperature. One of the drawbacks of Terfenol-D is its brittleness, which limits its ability to withstand shock loads or operate in tension.

The observed high magnetostriction values of 350 x 10 ^{- 6} in magnetic fields of и 100 Oe in Fe ₈₃ Ga ₁₇ and Fe ₈₁ Ga ₁₉ alloys [3–6] have contributed to a new stage in the study of magnetostrictive materials. In contrast to Tb ₀,₂₇ Dy ₀,₇₃ Fe ₂ , Fe-Ga alloys have high tensile strength ( ~ 500 MPa), weak temperature dependence of magnetomechanical properties ( - 20 0 C to 80 0 C), are inexpensive and corrosion resistant. Moreover, 3/2A _s reaches two positive peaks around 19 at.% Ga (380 x 10 ^{- 6} for quenched alloys) and

27 at.% Ga (440 x 10 - 6 for quenched alloys) [7]. Studies of Fe _{100 - x} Ga x binary alloys over the last 2 decades have revealed the dependence of 3/2A _s on Ga concentration, elastic properties, and formation of phase composition depending on production and quenching technology [7–12]. In particular, the region of the first magnetostriction peak is associated with the disordered A2 body centered cubic (bcc) structure. The metastable phase diagram of Fe _{85 - 65} Ga _{15 - 35} [7, 8] alloys constructed on the basis of the investigations determines the boundaries of the A2/(A2+D0 ₃ ) and (A2+D0 ₃ )/D0 ₃ regions and their dependence on the technological process. The boundary of the single-phase A2 region extends up to 17,6 at.% Ga in slowly cooled samples and up to 20.6 at.% Ga in quenched samples depending on the time and temperature of subsequent isothermal annealing. The beginning of the D0 ₃ phase boundary varies from 22,1 at.% to 23,4 at.%, which, in turn, affects the width of the (A2+D0 ₃ ) region. Similar studies carried out by X-ray diffraction methods [13,14] of similar compositions Fe ₈₀,₅ Ga ₁₉,5 and Fe ₈₀ Ga ₂₀ detected two phases in slowly cooled samples (67% A2 + 33% D0 3 ) and (30% A2 + 70% D0 3 ), respectively, whereas in quenched samples only the A2 structure was observed.

Initially, the version of the origin of MA proposed by Clark et al. [15] was that shortrange ordered Ga pairs form clusters that act as locally distorted anisotropic defects cause strain of a-Fe lattice along the [100] directions under application of magnetic or stress fields. Later, several inclusions of the D0 ₃ phase structure with a scale of < 2 nm in the A2 cubic matrix were found in Fe 81 Ga 19 alloys using high-resolution transmission electron microscopy [16–21]. These D0 ₃ nanoprecipitates can be transformed into the body-centered tetragonal (bct) phase D0 ₂₂ (L6 ₀ ) via diffusionless lattice rearrangement under the action of Bain stresses and, as a consequence, cause local deformation of the surrounding matrix, which leads to hight magnetostriction values.

To enhance the tetragonal magnetostriction, binary Fe 83 - 81 Ga 17 - 19 systems were doped with rare earth (RE) elements [22–28]. RE atoms have strong local magnetocrystalline anisotropy due to the large spin-orbit coupling and the highly anisotropic localized nature of the 4 f electron charge distribution. Together with the large atomic radius compared to Fe and Ga atoms, this can lead to a local deformation effect in the FeGa lattice due to the inclusion of the RE element and, as a consequence, higher magnetostriction values. Focusing on Tb-doped Fe–Ga alloys, Jiang et al. reported an increase in magnetostriction from 72 to 160 x 10 ^{- 6} in directionally solidified Fe ₈₃ Ga ₁₇ Tb _x (x = 0, 2) [23] polycrystalline alloys. Using three methods (casting, melt-quenching and melt-spinning) to produce Tb-doped alloys (Fe ₀,₈₃ Ga ₀,₁₇ ) _{100 - x} Tb x (x = 0 — 0,47), Wu et al. [22] showed that the solid solubility of Tb atoms in A2 matrix increases with increasing the cooling rate. Magnetostriction is greatly improved when solid Tb is dissolved in Fe ₈₃ Ga ₁₇ alloys, and giant values of perpendicular magnetostriction up to — 886 x 10 ^{- 6} were achieved in (Fe _0,83 Ga ₀,17 ) 99,77 ^Tb 0,₂₃ ribbons prepared by spinning from the melt. The data obtained in the experimental work [26] reflect the effect of Er addition on the microstructure and magnetic and microstructural properties of Fe ₈₃ Ga ₁₇ Er _x (0 < x < 1, 2). It was shown that the optimal addition of Er x = 0, 6 at.% increases the magnetostriction value up to 170 ppm in the [110]-textured polycrystalline Fe ₈₃ Ga ₁₇ Er ₀,₆ sample, which is ^ 275% higher than that of the corresponding parent Fe ₈₃ Ga ₁₇ compound. Based on experimental and computational studies conducted by He et al. [24], it is surmised that the giant magnetostriction in rare-earth doped FeGa alloys may be ascribed to the presence of nanoheterogeneties in the samples. The study of order-disorder phase transitions in

Fe ₈₁ Ga ₁₉ alloys doped with trace amounts ( < 0, 2 at.%) of rare earth elements (RE = Dy, Er, Tb, Yb) by neutron diffraction is presented in [29]. Slow heating and subsequent cooling of the alloys (at a rate of ± 2 K/min) leads to the formation of D0 3 phase clusters with sizes in the range of 200 – 300 A in a matrix of disordered A2 phase. The size and volume fraction of the clusters ( ^ 0, 3 of the sample volume) depend weakly on the specific composition. A search for structural ordering corresponding to the modified D0 ₃ phase (D0 ₂₂ ), which was found in a number of electron diffraction studies, did not lead to a positive result.

This study examines the impact of RE-atoms addition on the structural, magnetic and magnetostriction properties of Fe ₈₀,₄₇ Ga ₁₈,₇₅ RE ₀,₇₈ (RE = Tb, Pr, Er) alloys with the D0 ₃ phase within the context of density functional theory (DFT) at zero temperature and the Monte Carlo (MC) method at finite temperatures.

1.    Computational Details

The study of the structural, elastic and magnetostrictive properties of Fe 80,47 Ga 18,75 RE 0,₇₈ (RE = Tb, Pr, Er) alloys was carried out within the framework of the projector augmented-wave (PAW) method, as implemented in the ab initio software package VASP [30, 31]. The exchange correlation energy was treated within the generalized gradient approximation in the Perdew, Burke and Ernzerhof parametrization [32]. The electron-ion interactions were described using PAW potentials with the following electronic configurations: 3p ⁶ 3d ⁷ 4s ¹ for Fe, 3d ¹⁰ 4s ² 4p ¹ for Ga, 5s ² 6s ² 5p ⁶ 5d ¹ for Pr, 6s ² 5p ⁶ 5d ¹ for Tb, and 5p ⁶ 5d ¹ 6s ² for Er. The plane-wave cut-off energy was set to 650 eV. A Monkhorst-Pack scheme with a k-point density of 4 x 4 x 4 was employed to integrate the Brillouin zone in inverse space. The convergence criteria for the total energy was set to 10 ^{- 6} eV/atom.

The geometrical optimization procedure was performed for the Fe ₈₁,₂₅ Ga ₁₈,₇₅ and Fe 80,47 Ga 18,75 RE 0,₇₈ compounds formed on a 128-atom supercell by translating the elementary 16-atom unit cell of cubic symmetry D0 ₃ (F m3m group of symmetry, No 225) in 2 x 2 x 2 directions. For the binary composition Fe ₈₁,₂₅ Ga ₁₈,₇₅ in the 128-atom supercell, 24 Ga atoms were placed at the Wyckoff 4a-positions with coordinates (0, 0, 0). Three types of iron atoms labeled as Fe ₁ (8 atoms), Fe ₂ (32 atoms), and Fe ₃ (64 atoms) were located at the Wyckoff positions 4a (0, 0, 0), 4b (0,5, 0,5, 0,5), and 8c (0,25, 0,25, 0,25), (0,75, 0,75, 0,75), respectively. For ternary alloys, one atom of iron located at Ga-sublattice (4a positions) was replaced by an atom of RE (Fe 103 Ga 24 RE 1 ). Fig. 1 shows the 128-atom supercell of Fe ₁₀₃ Ga ₂₄ RE 1 , representing Fe ₈₀,₄₇ Ga ₁₈,₇₅ RE ₀,₇₈ with the D0 ₃ crystal structure. In the upper right corner of Fig. 1, an image of a rare earth element is shown surrounded by iron atoms of the first and second coordination spheres (CS).

The calculation of the tetragonal shear modulus C ‘ = (C 11 — C ₁₂ ) /2 required to estimate the values of the magnetostriction constant was carried out using the strainstress method [33]. In the elastic stress region σ = (σ 1 , σ 2 , σ 3 , σ 4 , σ 5 , σ 6 ) the response of solids to deformation under the application of an external load ε = (ε 1 , ε 2 , ε 3 , ε 4 , ε 5 , ε 6 ) satisfies the generalized Hooke’s law and can be simply represented in the Voigt notation a i = Е б₌₁ C ij ^£ j • The elastic stiffness tensor C ij was determined using the first-order derivative of the stress-strain curves proposed by Nielsen and Martin [33] with the magnitude of strain e = ± 1, 5%.

The magnetostriction coefficient λ 001 was determined through the magnetocrystalline anisotropy energy (E _MCA ), the elastic modulus C ^′ , and the magnetoelastic coefficient b ₁

from the following equation [34]:

^ 001 —

^{2 dE} MCA / ^de z

3d ² E_to t /de l

bl   , _ ² dE MCA

3C’ - ^{1 —} 3V 0 de z

ε _z is the tetragonal strain, V ₀ is the cell volume. E _MCA is the maximum value of the energy difference of the magnetic system when the spins are directed along the different quantization axis. In the present paper, the Fe/RE magnetic moments were rotating from z-axis to [111] direction and E _Mca — E [₀₀₁] — E [111] . To determine E [₀₀₁] and E [111] , the supercells were deformed from their optimized geometries along the z-axis in the constant volume mode with the strain value e z — ± 1, 5%. Self-consistent calculations taking into account spin-orbit coupling were performed in the non-collinear VASP mode.

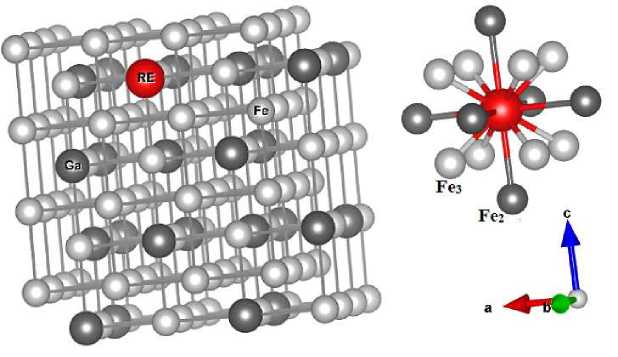
Fig. 1 . The 128-atom supercell of Fe ₁₀₃ Ga ₂₄ RE ₁ , representing Fe _80,47 Ga _18,75 RE _0,78 with the D0 ₃ crystal structure. The two nearest coordination spheres of the element RE are shown in the upper right corner: the light gray spheres correspond to the first shell, and the dark gray spheres to the second. Iron, labeled Fe ₂ and Fe ₃ , occupies the Wyckoff sites 4b and 8c, respectively. In the binary compound Fe ₈₁,₂₅ Ga ₁₈,₇₅ , the element RE corresponds to Ga

Based on the calculated equilibrium lattice constants a ₀ , the SPR-KKR [35] package was used to calculate the parameters of the Heisenberg magnetic exchange coupling J _ij . The constants J _ij were calculated using the expression proposed by Liechtenstein et al. All calculations were converged to 0,01 mRy of total energy.

The final step was the Curie temperature estimation with the help of the MC simulations of the three-dimensional Heisenberg model Hmag — — ^j JijSiSj• Here Si — (Six,S/, Sz) is a classical magnetic degree of freedom |Si| — 1. Using the calculated Jij, Fe (µFe) and RE (µRE) magnetic moments as input data, the finite-temperature MC simulations of Heisenberg model without magnetic field and anisotropy terms were done. The model lattice with periodic boundary conditions was performed on N — 3456 atoms lattice with periodic boundary conditions using the Metropolis algorithm [36]. The D03 structure was a 6 x 6 x 6 array of 16-atoms unit cells. As time unit, we used on MC step consisting of N attempts to change the spin variables. The total number of MC steps per the temperature step was 106. The Curie temperature was estimated from the magnetization-temperature curves M (T) by plotting the linear intersection of the function M1/e with the temperature axis. Here в — 0,365 is the critical index for the three- dimensional Heisenberg model. The listed calculation stages are presented in more detail in our previous articles [37–42].

• 2.    Results and Discussions

  2.1.    Structural Properties

  At the first stage of the study, the influence of RE elements on the structural properties of Fe₈₁,₂₅Ga₁₈,₇₅alloys was evaluated. Fig. 2 (a) shows the calculated values of the atomic volume V_a = V_o/N (N = 16 for D03 structure) and elastic moduli C‘ depending on the number of 4f -electrons. As can be seen from Fig. 2 (a), the addition of RE elements increases the cell volume per atom by ≈ 1%. This result is expected due to the significantly larger atomic radius of Pr (1,82 ^˚A), Tb (1,77 ^˚A) and Er (1,76 ^˚A) than that of Fe (1,26 ^˚A) and Ga (1,35 A). From the lattice parameters along different directions shown in Fig. 2 (a), it is evident that replacing one Fe atom with a RE results in a slight degree of tetragonality (a/c < 0, 0001). The addition of RE atoms to the (Fe₈₃Ga₁₇)_100-xREx [26,28,43] alloy experimentally confirms the fact of an increase in the lattice parameter. The difference in atomic dimensions leads to low solid solubility of RE in the bcc FeGa matrix, and thus, RE exists mostly in the precipitates [26]. X-ray diffraction data of (Fe₈₃Ga₁₇)_100-xErx alloys indicates the presence of a single phase having the bcc crystal structure for all samples of composition x < 0, 6 (lattice parameter was found a = 2, 905 ± 0, 005 A). In the case of (Fe₈₃Ga₁₇)₉₉,₉₄Pr₀,₆, the lattice constant of A2 phase was found to be ^ 2, 904 A [43], which is closer to (Fe₈₃Ga₁₇)₉₉,₉₄Tb₀,₆(a = 2, 9036 A) [28].

2.2.    Magnetostrictive Properties

(a)           Number of 4/'-electrons         Ф)           Number of 4/'-electrons

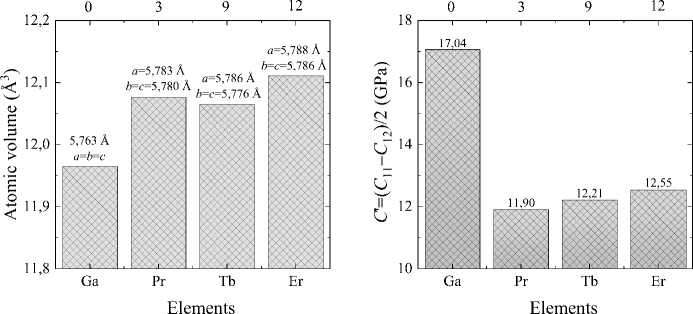
Fig. 2 . The calculated (a) atomic volume V a = V 0 /N , and (b) shear modulus C ‘ for Fe 81,25 Ga 18,75 , and Fe 8o,47 Ga 18,75 RE o,78 alloys with D0 3 structure depending on the number of 4 f -electrons. a , b and c corresponds to the length of vectors along axis x , y and z

Calculation of elastic moduli showed that in the D0 3 phase, the addition of a rare earth metal atom leads to significant softening C ^′ (see Fig. 2 (b)). In this case, the Fe ₈₀,₄₇ Ga ₁₈,₇₅ Er ₀,₇₈ alloy has the largest value C ‘ = 12, 55 GPa, which is due to the smaller atomic radius of Er compared to Pr and Tb. It is likely that a large number of 4 f valence electrons and aspherical charge cloud distributions observed in Er atoms lead to enhanced magnetic anisotropy due to crystalline electric field effects.

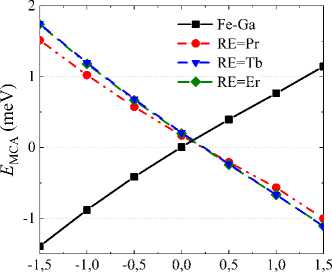
Recently, many studies have focused on the effects of trace doping with rare earth elements, which have a large number of 4f valence electrons, a non-spherical charge cloud distribution, and strong magnetocrystalline anisotropy between orbitals and spins [43]. It was found that the magnetostriction of Fe–Ga alloys can be enhanced by introducing Tb, Dy, or other rare earth elements. The enhancement of magnetic anisotropy is attributed to the preferential grain orientation and tetragonal distortion induced by the solid solution of rare earth atoms [43]. Fig. 3 (a) shows the calculated magnetocrystalline anisotropy energy E MCA as a function of tetragonal distortion ε for Fe 81,25 Ga 18,75 and Fe 80,47 Ga 18,75 RE 0,78 alloys in D0 ₃ structure. The magnetocrystalline anisotropy energy was defined as the energy difference between magnetization along the direction of uniaxial stress and its perpendicular E _Mca = E [ooi] — E [111] • The E _Mca (e) deformation dependence shows linear behavior with a positive slope in the binary compound. Addition of RE atoms changes the slope to negative. This fact indicates that, compared to Fe ₈₁,25 Ga ₁₈,75 , the [001] direction is not the most stable spin orientation for systems with Fe _80,47 Ga _18,75 RE _0,78 .

(a)

e (%)

Fig. 3 . (a) Calculated magnetocrystalline anisotropy energy E MCA as a function of tetragonal distortion ε and (b) tetragonal magnetostriction coefficient λ ₀₀₁ for Fe _81,25 Ga _18,75 and Fe _80,47 Ga _18,75 RE _0,78 alloys in D0 ₃ . The most stable directions of orientation of magnetic moments are indicated in square brackets

Ф)           Number of ^/"-electrons

Elements

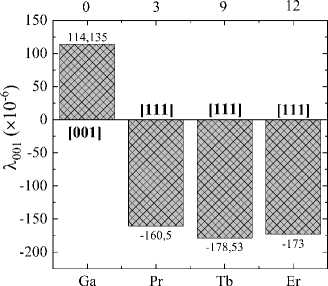
Fig. 3 (b) shows the constants λ 001 calculated according to (1). Replacing one Fe atom with a RE atom increases the magnetostriction value, while in the Fe 80,47 Ga 18,75 Tb 0,78 composition the absolute value of A ₀₀₁ ^ - 179 x 10 — 6 is the largest. In our case, the effect of 0,78 at.% terbium on magnetostriction is 19% in D0 ₃ . The calculation of λ ₀₀₁ performed using the DFT in the A2 [44] structure for the Fe _79,69 Ga _19,53 Tb _0,78 and Fe _77,78 Ga _20,37 Tb _1,85 alloys showed an increase in magnetostriction by 68% and 59%, respectively, relative to the Fe 81,48 Ga 18,52 alloy.

In [24], for Fe83Ga17M0,2 (where M are RE dopants from La to Lu), the dependence of the transverse magnetostriction on the number of 4f electrons was constructed. The biggest excess magnetostriction was found for Ce, Pr, Tb, and Dy, the atoms with the largest negative quadrupole moments. The calculation value of λ001 in Fe80,47Ga18,75Pr0,78 is the smallest among alloys with RE atoms. Experimental work shows that rare earth elements have low solubility in the Fe–Ga solid solution and in most cases the addition of a small amount of ^ 0,1 at.% leads to formation of secondary phases of lower symmetry in the bcc matrix [22, 23, 25–28]. Thus, it can be concluded that the possible increase in magnetostriction in Fe–Ga-RE alloys near the first magnetostriction peak is due to an increase in anisotropy both in the bcc matrix itself and in inclusions.

2.3.    Magnetic Exchange Constants and Curie Temperature

Analysis of the calculated magnetic moments given in Table for Fe ₈₁,₂₅ Ga ₁₈,₇₅ and Fe ₈₀,₄₇ Ga ₁₈,₇₅ RE ₀,₇₈ alloys shows that replacing one Fe atom with RE has no significant effect. Ga, as well as RE atoms, align antiferromagnetically with Fe, with magnetic moments of ^ Ga = - 0, 11^ _b /atom and ^ r_E = - 0, 28 4— 0, 55^ _B /atom, and are associated primarily with the p- and d- orbitals, respectively. The atomic radius of Er is smaller than that of Pr and Tb, resulting in Fe ₃ atoms in first CS of Er having a higher magnetic moment than the same atoms in Fe ₈₀,₄₇ Ga ₁₈,₇₅ (Pr,Tb) ₀,₇₈ alloys.

Table

Calculated values of the total magnetic moment µ _tot (µ _B /atom), the average magnetic moment per Fe atom Д _Ғе (^ _B /atom) and partial magnetic moments of three types of Fe atoms ^1 , 2 , 3 , ^ Ga and ^ re (^ в /atom) for Fe 8i,25 Ga i8,75 and Fe 80,47 Ga i8,75 RE o,78 alloys in D0 3 . The iron atoms labeled as Fe 1 , Fe ₂ , and Fe 3 are located at the Wyckoff positions 4a (0, 0, 0), 4b (0,5, 0,5, 0,5), and 8c (o,25, 0,25, 0,25), (0,75, 0,75, 0,75), respectively

Alloy	µ tot	^ Fe	µ Fe 1	µ Fe 2	µ Fe 3	µ Ga	µ RE
Fe 81,25 Ga 18,75	1,87	2,33	2,51	2,44	2,25	— 0, 12	^^^^^^
Fe 80,47 Ga 18,75 Pr 0,78	1,84	2,32	2,50	2,45	2,23	— 0,11	— 0, 28
Fe 80,47 Ga 18,75 Tb 0,78	1,83	2,32	2,50	2,44	2,23	— 0,11	— 0,46
Fe 80,47 Ga 18,75 Er 0,78	1,88	2,37	2,54	2,46	2,31	— 0,11	— 0, 55

For all compounds the magnetic exchange coupling parameters J ij were calculated using the equilibrium lattice parameters and the SPR-KKR package by employing coherent potential approximations. The FM state of D0 ₃ structure was considered for Fe _{81 , 25} Ga _{18 , 75} , and Fe 80 , 47 Ga 18 , 75 RE 0 , ₇₈ (RE = Tb, Pr, Er) alloys. Figs. 4 (a)–(c) show the dependence of J ij on the distance d/a between atoms i and j for the first three coordinate spheres.

The magnetic exchange parameters demonstrate the oscillatory behavior and decay with the interatomic distance for all compounds under consideration. Exchange interactions J G a ^Fe/RE are small and are not included in the consideration. As it shown in earlier studies of J ij in Fe-based alloys [40-42], the main contribution to the exchange interaction in D0 ₃ structure is made by Fe atoms located on different sublattices. In the case of the Fe 81 , 25 Ga 18 , 75 alloy (see Fig. 4 (a)), the exchange interactions are about 24 and 22.5 meV between Fe 3 -Fe 2 and Fe 3 -Fe 1 , respectively. The addition of Pr and Tb does not affect the above interactions between iron atoms. In the case of Er, j j ^{- Fe} 1 drastically decreases from 22.5 meV to ^ 1 meV. Such a significant change in magnitude may be the result of exchange interaction between Fe and Er atoms. Fig. 4 (c) shows the values of exchange interactions of RE atoms with Fe atoms located on different sublattices. The Er-Fe 3 and Er-Fe 2 interaction in the first and second coordination spheres (see for detail Fig. 1) J ij ~ — 3 meV that indicates antiferromagnetic interactions.

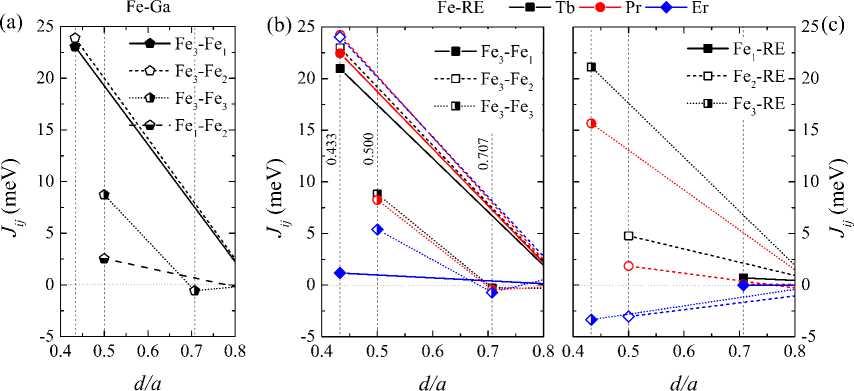
Fig. 4 . Calculated exchange coupling parameters J ij as a function of distance (d/a) between atoms i and j for (a) Fe ₈₁,₂₅ Ga ₁₈,₇₅ , and (b, c) Fe ₈₀,₄₇ Ga ₁₈,₇₅ RE 0,₇₈ (RE = Tb, Pr, Er) alloys. The vertical dotted lines indicate the distance of the first three coordinate spheres d/a = 7 3/4,1/2, 7 2/2

The constants of magnetic exchange interactions and magnetic moments obtained from ab initio calculations were used further as input parameters in Heisenberg model to simulate the temperature dependencies of magnetization by MC approach.

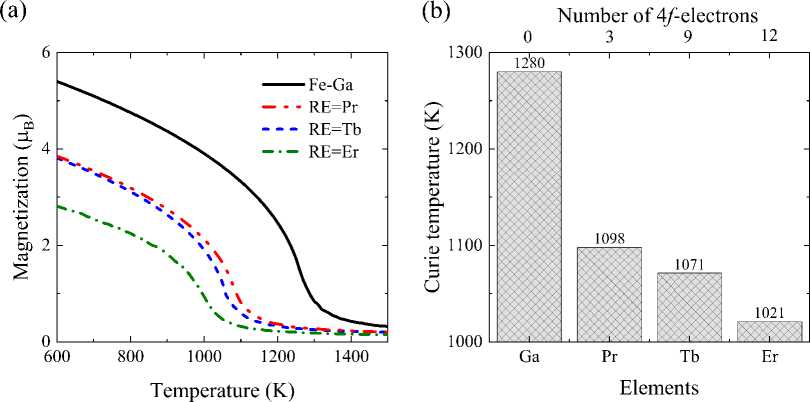
Fig. 5. (a) Theoretical temperature dependence of magnetization and (b) Curie temperature of Fe81,25 Ga18,75 , and Fe80,47Ga18,75Re0,78 alloys

The constants of magnetic exchange interactions and magnetic moments obtained from ab initio calculations were further used as input parameters for modeling the temperature dependence of magnetization (M). Fig. 5 (a) shows the curves of the M(T) dependence of Fe81,25Ga18,75 and Fe80,47Ga18,75RE0,78 alloys with the D03 structure in the temperature range from 600 to 1500 K using MC modeling of the classical three-dimensional Heisenberg model, performed in zero magnetic fields. The M(T) curves of compounds with RE atoms have lower magnetization, indicating that the magnetic interactions weaken upon introduction of RE atoms, in particular, the Fe-RE-Fe interactions remain weaker than FeFe interactions under thermal perturbations. This behavior is confirmed by experimental results. In the work [43], a decrease in the saturation magnetization in the alloy (Fe83 Ga17)100-xPrx (x = 0 ^ 1, 0 at.%) was shown with increasing Pr concentration. Thus, REs contribute to the local paramagnetic ordering in Fe81,25Ga18,75 rather than to the strengthening of ferromagnetic interactions.

This decrease in the strength of ferromagnetic interactions leads to a decrease in the Curie temperature T C , shown in Fig. 5 (b). A directly proportional dependence of T C on the number of electrons in the 4f -orbital can be traced: the more f -electrons, the lower the Curie temperature. In the Fe ₈₀,₄₇ Ga ₁₈,₇₅ Er ₀,₇₈ alloy, T c is 20% lower compared ^to Fe 81,25 Ga 18,75 ^.

Conclusion

The present paper reports on the results of ab initio calculations obtained by the DFT method at zero temperature and the MC method at finite temperatures in various compositions with the D0 3 structure. In particular, the results related to the structural and magnetic properties of Fe ₈₁,₂₅ Ga ₁₈,₇₅ and Fe ₈₀,₄₇ Ga ₁₈,₇₅ RE ₀,₇₈ (RE = Pr, Tb, Er) alloys are reported. The equilibrium lattice parameter increases with the replacement of the Fe atom by a RE. The presence of RE atoms in the lattice leads to a slight deviation of cubic symmetry to tetragonal. All the compounds considered are mechanically stable, and the addition of RE elements leads to a softening of the shear moduli C ^′ . The largest value of tetragonal magnetostriction A ₀₀₁ ^ - 179 x 10 — 6 is observed for Fe ₈₀,₄₇ Ga ₁₈,₇₅ Tb ₀,₇₈ , and the effect of 0,78 at.% terbium on magnetostriction is 19% compared to Fe ₈₁,₂₅ Ga ₁₈,₇₅ . The addition of rare earth elements leads to a decrease in the Curie temperature, the lowest temperature being found in the Fe 80,47 Ga 18,75 Er 0,78 alloy. This behavior is due to the presence of antiferromagnetic exchange interactions between Er and Fe atoms in the first and second coordination spheres.

Acknowledgments. This study was supported by the Russian Science Foundation, project no. 24-22-20086,