Effect of Rician Factor in Satellite Communication Signal with MAP-MQAM Demodulation

Mobile wireless communication system can be described as any communication system that can be moved during operation. It has made a tremendous impact on the lifestyle of human beings by providing high quality of voice as well as data traffic services to users, especially in some economic sectors such as telecommunication, broadcasting, education, marketing, security, automobile to mention but few [1].

* Corresponding author. Tel.: +2348033889921

In mobile telecommunication network such as Global System for Mobile communication (GSM), signal propagation can be made between the transmitter and receiver either from mobile station or Base transceiver station, or relay stations or mobile switching centre and vice-versa using microwave radio and sectorial antenna. Sometimes the height of the mobile antenna may be much lower than the surrounding structures such as high scraper buildings, mountains, trees etc. In this case, the existence of a direct line of sight (LOS) path between the transmitter and the receiver is highly unlikely. Also, moving objects such as cars, lorries, foliage can obstruct the LOS and result in diffraction and reflection of the transmitted signal [2-3]. Consequently, transmitted signal arrives at the receiver via several paths with different time delays creating a multipath propagation at the receiver. These multipath propagations have randomly distributed amplitudes and phases and the net effect is the fluctuation of the received signal known as fading [2], [4-5].

In mobile satellite communication, received signals through troposphere experienced atmospheric effects such as refraction, scintillation, attenuation and Doppler spread when there is relative motion between the transmitter and receiver [6]. In satellite communication there is the existence of dominant Line of Sight (LOS) signals among the multipath components. As a result of this, rician distribution is therefore used to model the phenomenon of the satellite signal. Some of the digital modulators previously in use are faced with challenges of high data rate, Doppler Effect, maximum channel bandwidth, higher modulation order effect and so on. In this paper, conventional M-QAM was considered because it is largely used in high capacity radio communication systems. QAM is a modulation technique where its amplitude is allowed to vary with phase. QAM signaling can be viewed as a combination of Amplitude Shift Keying (ASK) and Phase Shift Keying (PSK). That means the digital information is carried in both the phase and the amplitude of the carrier signal [79].

The flow of bits transmitted is split into two equal parts generating two independent signals to be transmitted and encoded separately. Then, one channel ("inphase") is multiplied by a cosine, while the other channel ("quadrature") is multiplied by a sine. In this case there is a phase of 90° between them and then simply added the Inphase signal to Quadrature signal and sent through the real channel [1],[10-13]. The channel model was developed and the system model was developed around it, simulated to see the effect in the presence of rician distribution at different rician factors. The performance of the conventional M-QAM was compared with the developed MAP-MQAM in term of probability of error known as Bit Error Rate (BER). It was confirmed that probability of error depends on the rician factor, speed of the satellite and the order of modulation.

The remainder of this paper is organized as follows. In section II the system model for the mobile wireless communication system was developed using MAP-QAM demodulator at the receiver,. Section III describes the simulation model of the mobile wireless communication system. In Section IV the results and discussion of the simulation are provided while Section V gives the conclusion of the study.

Nomenclature
ASK	Amplitude shift keying
AWGN	Additive white Gaussian noise
BER	Bit error rate
LLR	Logarithm of Likelihood Ratio
LOS	Line of sight
MAP	Maximum a Posteriori
ML	Maximum likelihood
PSK	Phase shift keying
QAM	Quadrature amplitude modulation
SNR	Signal to noise ratio
SRRCF	Square Root Raised Cosine Filter

• 2.    System Model

The system model consists of a transmitter, the mobile satellite channel and a receiver. 1,000 randomly generated binary data are reshaped and modulated with QAM signalling schemes. This modulated data was further up-sampled by a factor of 16. The up sampling factor of 16 was the standard used in [14], [2] and was used to multiply the sampling rate; therefore creates a 16 f new sampling rate of the transmitted signal. This was achieved by filling 15 zeros between each signal. The higher the number of up-sampling factor the better is the quality of the received signal.

The up-sampled signals are passed through a Square Root Raised Cosine (SRRC) pulse-shaping filter before being transmitted to match the filter used at the receiver to maximize the system SNR at the output. The output of the SRRC pulse shaping filter was then transmitted over the rician fading channel and resulting signal was added to AWGN channel. The rician channel was used to model the satellite signal path

Therefore, the channel was developed by generating the rician fading process and multiplying it with the transmitted signal. Effect of the Doppler frequency ‘ f ’ which is directly related to the velocity of the mobile receiver, was introduced in the mathematical model of the mobile system. The rician fading channel was simulated at mobile speed of 90km/h. At a carrier frequency of 900MHz, the corresponding maximum Doppler frequency f is 76 Hz. The system model with rician fading factor ( k ) of 5, 10 and 15 on the received signal was simulated.

At the receiver, the matched filter was used for detection of pulse signal in presence of AWGN to maximize the signal power, and minimizes the noise power. The matched filter section matched the signal with the help of filter coefficients and the signal was passed through the down sampler for down sampling purpose, which can be done by considering the 1st symbol, 17th symbol, and 33rd symbol and so on. Then MAP QAM demodulator demodulated these symbols into the bit form by probability estimation method. The last section in the design is BER calculator, which was used to calculate BER by comparing the input bits at the receiver and transmitter. MAP-QAM demodulator and system model developed are shown in Fig. (1) and Fig. (2).

The modulated signal S ( t ) can be modeled as

S_QAM ( t ) = A_c ²cos( θ ( t ))cos(2 π f_ct ) - A_c ² sin( θ ( t ))sin(2 π f_ct ) (1)

where A is carrier wave amplitude, f is the carrier frequency, θ ( t ) is the phase angle and T is the symbol period.

Equation (1) can be written in terms of Inphase and Quadrature forms as:

SQAM (t) =I(t)cos(2πfct) -Q(t)sin(2πfct)

where I(t) = A j 2 cos θ(t) , Q(t) = Ac  2 sinθ(t), θ(t) = 2π and M’ is 4, 16 for quaternary QAM and 16-QAM respectively.

Mobile channel represented by the channel impulse response h ( t ) is modeled as:

hR(t)=σr exp(-r22σ+A22)Io(2Aσr2),  r≥0,A≥0.

where σ is the standard deviation, I (.) is the modified Bessel function and r is the envelope of the received signal obtained as r = (12( t) + Q 2( t ))1

where I ( t ) and Q ( t ) are the inphase and quadrature channels transmitted signal that have a standard deviation of a . Therefore, total power in the received signal is a ²

I ( Ar ) is the modified Bessel function of the first kind and zero order expressed by [6] as p 2n

I o ^ = n J o

-I

e

. ( Arr _ )_cos e 2 a ^{1 2}

de

The Rice factor ‘ k ’ is defined as the ratio of the dominant component to the power in all the other components and it can be expressed as kr=5(6)

Therefore, (3) can be re expressed as

Hr (t) = . exp(—  с)Io (kr x A),  r > 0, A > 0.

The received waveform r(t) at the input of matched filter can be expressed as r (t) = Hr (t).( S   . (t) * p (T)) + n (t)

p(t) is time impulse response of the Square Root Raised Cosine Filter (SRRCF) and is expressed as sin(n t (1—a ))+4 at cos(n t (1+a))

p(')=—ПГТ-(401)4—

Output of the matched filter m(t) was modeled using the convolution theory expressed as m (t) = r (t) * p (T -1)

where p(T — t) is time inverse function of the SRRCF impulse response expressed as sin(nT=t (1-a ))+4 aT—t cos(nT—t (1+a ))

p(T - t) =-------nT^t(V-^I— )2) (11)

Therefore

m ⁽ t ) = { ^{[ H} R ⁽ t ).^{( S} QAM ⁽ t ) * p ⁽ t ^{)] +} n ⁽ t ) } * p ^{( T} - t )

Effect of the convolution between r ( t ) and the p(T - t ) in (10) detects the transmitted S_ж(t ) signal from r ( t ) . The output of the matched filter m ( t ) was down sampled by factor of 16 to return the data rate to the original data rate before up sampling and symbolised as. y ( t ) . The detection using MAP QAM demodulation then followed the down sampling process. Conventional QAM demodulator can be obtained by splitting the y ( t ) into Inphase and Quadrature channels. At the inphase channel, the signal y ( t ) was multiplied by cos(2 n f_ct ) to detect the Inphase bits Y_t ( t ) while the other fading signal at the Quadrature channel the signal y_Q ( t ) was multiplied by sin(2nf_ct ) to detect the Quadrature bits y_q ( t ). where Y _; ( t )can be with the Doppler frequency on the received carrier at the Inphase channel

• Y, (t) = 21 (t) + КI (t )cos(4n(fc + /^ ) t)]

where I ( t ) is the signals to be detected at the Inphase channel. The same process was repeated for the y ( t ) at the Quadrature channel but with cosine function was replaced by sine function to obtain:

Yq (t) = 2 Q (t) + MQ (t )sin(4n( fC + fd ) t)]

The bits from these channels were combined to one symbol which can be represented as:

= [Y,Yq ]

MAP detection was carried out separately on each of the two QAM signals at the Inphase channel and Quadrature channel. MAP QAM can be obtained by taking the Logarithm of Likelihood Ratio as

LLR(y) = |Ny ] / ln( p)(16)

where N random variable Gaussian noise variance and a is the coded data taken to be 1 in this paper.

Fig. (1) and Fig. (2) are the MAP-QAM and mobile wireless communication system respectively.

p is the ratio of priori probabilities which was as py , where p = 1 for equiprobable, (16) can be further expressed as

• > N ₃ ln( p )

y (17)

The hypothesis in the mobile communication problems are usually as equiprobable as:

p 0 = P x = 2                                                                             ⁽¹⁸⁾

Therefore, for equiprobable as seen in (18), ln( p ) = 0 and MAP detection proposed by the Bayes is equivalent to the Maximum Likelihood (ML). The probability of error adopted in this paper was the model proposed by [15] given as

P (e) = Pr (e / H = 1) = Pr (e / H = 0) = Q f E)

N o )

For n number of Binary data to be transmitted, the modulated q bits can be vectored as

• q=[ qQn qin qh -1 qQn -1 • • • qQ 1 qi 1 qQ 0 qi 0 ]

^^^^

That is q_H q^_h take the value of the hypothesis decisions for binary 0 and 1; H = 0 and H = 1 , where

• 0 <  i <  n .

• 3.    Simulation Method

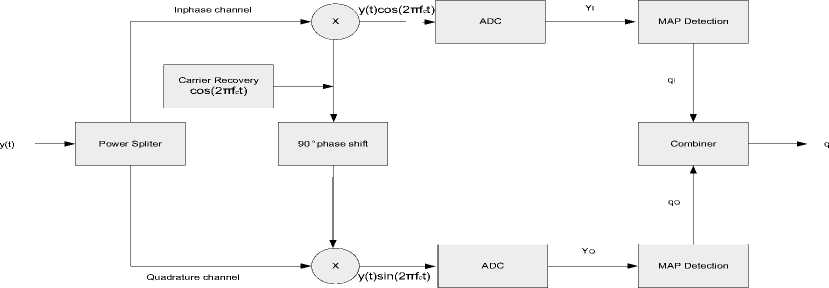
Fig.1. The MAP QAM Demodulator

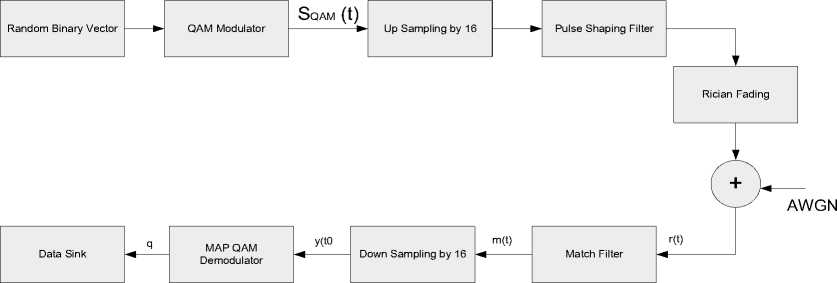
Fig.2. The Mobile Wireless Communication System Simulation Model

The simulation of the system model developed was carried out using MATLAB application package because of the controllability and repeatability of parameters, which is very hard with field test.

The following parameters and system configurations were used as shown in Table 1.

Table 1. Simulation Parameters

Description	Parameter
Modulation scheme:	MQAM
Carrier frequency:	900MHz
Bandwidth of signal Symbol periods, Ts :	20kHz for 4QAM and 22MHz for 16QAM 7.41µs for 4QAM and 0.15µs for 16QAM
Delay spread τ :	50ms for 16QAM and 6µs for 4QAM
Noise:	AWGN
Transmit Filter Receive Filter Mobile speed Fading type Rician factor	Square root raised cosine pulse shaping Matched Filter 90km/h Rician Fading 5, 10, 15

• 4.    Results and Discussion

  The results of the effect of rician factors k = 5, 10, and 15 in satellite communication with and without MAP-MQAM demodulator at the receiver are presented in Fig. (3) to Fig. (6). Fig. (3) shows the BER values against SNR with conventional 16 QAM at rician factors k = 5, 10, and 15. It can be observed that at SNR of 2dB, rician factors k = 5, 10, and 15, BER values obtained are 0.0455, 0.0343 and 0.0301 respectively with conventional 16 QAM at 90 km/h. Also at SNR of 3dB, rician factors k = 5, 10, and 15, the BER values decreased to 0.0361, 0.0263 and 0.00201.

Fig. (4) Shows the BER values at rician factors k = 5, 10, and 15 using MAP-16QAM. It was observed that the BER values of 0.0287, 0.0204 and 0.0180 were obtained respectively at SNR of 2dB, while at SNR of 3dB, 0.0230, 0.0155 and 0.095 values of BER were obtained for k = 5, 10 and 15 respectively.

Fig. (5) Depicts the BER values obtained at different SNR with conventional 4QAM demodulator. At SNR of 2dB, 0.0060, 0.009 and 0.0002 were BER values obtained for k = 5, 10, and 15 respectively at speed of 90 km/h. With 4QAM-MAP demodulator, the BER values changed to 0.0048, 0.0006 and 0.0001 for k = 5, 10 and 15 respectively.

The results are justifiable in that as the order of QAM scheme increases, the constellation distance also reduces which in turn increase the BER value and degrade the performance. It was also observed that as rician fading factor ‘k’ increases, BER values decrease in both MAP-MQAM and MQAM. This is justifiable in that rician factor k depends on the LOS. The results obtained using rician distribution is in agreement with results obtained by [14] in which the system performance increases as ‘k’ increases.

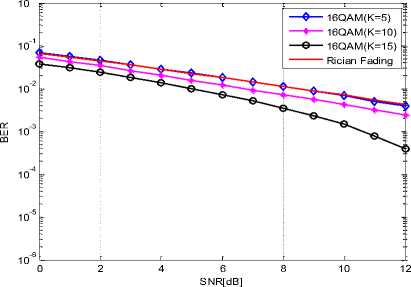
Fig.3. Simulation of BER Values Against SNR with Conventional.

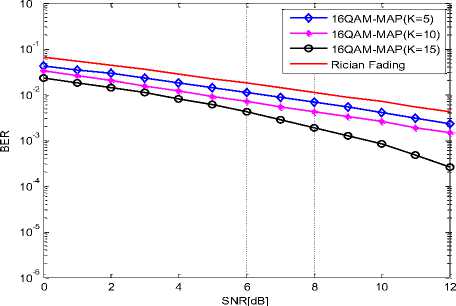
Fig.4. Simulation of BER Values Against SNR 16QAM; K = 5, 10 And 15 With MAP-16QAM; K = 5, 10 And 15.

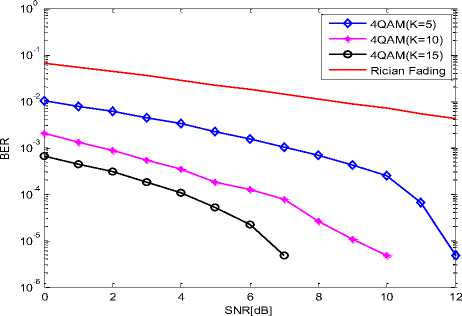
Fig.5. Simulation of BER Values Against SNR with Conventional

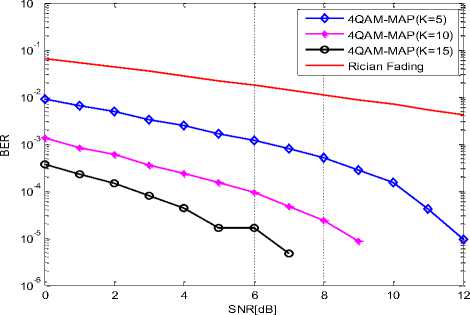
Fig.6. Simulation of BER Values Against SNR with K = 5, 10 And 15 MAP-4QAM; K = 5, 10 And 15.

• 5.    Conclusion

The effects of different rician factors over satellite communication with and without MAP-QAM demodulator have been investigated. The system model which consists of a transmitter, mobile satellite channel and receiver was developed. The receiver was developed around MAP-QAM demodulator. The model has been simulated using MATLAB software programme. The performance was evaluated using BER with conventional and MAP-MQAM at speed of 90 km/h. The results obtained showed that as the constellation size increased, the BER values decreased. Also, as the rician factor ‘k’ increases, BER values decrease in MAP-MQAM indicating better performance. This paper has shown that high rician factor with MAP-MQAM demodulator gave better performance.