Effects of basis set superposition error on DFT model of C2N/graphene bilayer

Due to its structural and electronic properties, graphene is a thoroughly investigated material in the field of nanoelectronics [1]. However, its usage in electronic devices is limited because of its zero band gap [2]. There are several approaches to opening the graphene band gap, one of them, which do not drastically affect the monolayer geometry, is the usage of a substrate with the needed characteristics [3]. Already successfully synthesized C₂N monolayer [4] has an atomic structure similar to graphene (except for the nitrogen pores), so it could become an appropriate substrate which will not induce considerable strains of graphene. To check this hypothesis, we can start the investigation with numerical simulations of the C₂N/graphene bilayer structure. Therefore, we aim to obtain the physically sound model of the C 2 N/graphene bilayer using the density functional theory (DFT).

Since the monolayers in the bilayer structure could be arranged differently, it could lead to a quite large simulation cell [5], which will result in time-consuming and heavy calculations with the plane waves (PW). This approach to wave function decomposition does not depend on the amount and type of atoms in the cell but could be cumbersome for modeling systems with large vacuum volumes. Alternatively, a basis set of localized pseudoatomic orbitals (PAOs) could give fast and less resourceconsuming results. However, the localized nature of PAOs gives rise to the basis set superposition error (BSSE) [6]. This error leads to an artificial attraction between the investigated subsystems [7]. Moreover, it could be especially significant for cases where subsystems are similar in size. Therefore, to check how strongly this BSSE could influence the calculated properties of the C2N/graphene bilayer, we simulated this structure using both PW and PAO basis sets.

Models and simulation details

Calculations with the localized pseudo-atomic orbitals were performed via the SIESTA software package [8]. For plane-wave simulations, we used the VASP code [9]. In both packages, the periodic boundary conditions were implemented. Pseudopotentials for the SIESTA calculations were taken from the FHI database [10]. For VASP modeling we utilized the 2012 version of pseudopotentials. 2s²2p² electrons for С and 2s²2p³ electrons for N were considered valence. Since the interaction between C 2 N and graphene layers is mostly weak (via van der Waals force), we used the generalized gradients approximation, GGA (Perdew–Burke–Ernzerhof functional, PBE [11]), with the Grimme semi-empirical dispersion corrections, DFT-D2 [12], and the vdW exchange-correlation functional of Dion et al. [13]

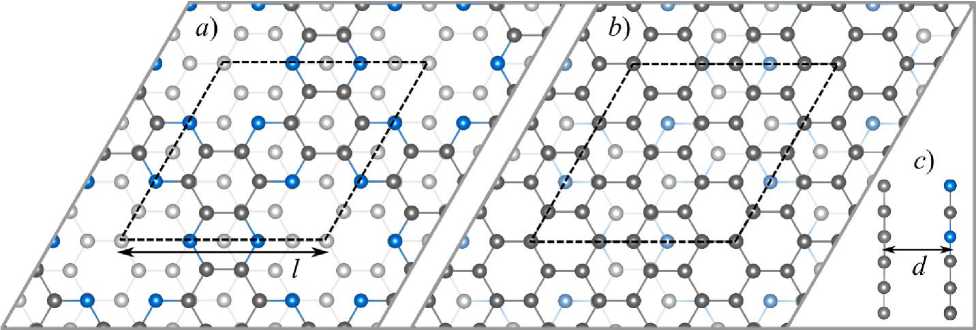
Fig. 1. Simulated structure of the C 2 N/graphene bilayer: top views from a ) C 2 N and b ) graphene side; c ) side view. Carbon and nitrogen atoms are represented as grey and blue balls, respectively. Cell boundary is noted by a black dashed line

The hexagonal simulation cell contained 1 unit cell of C 2 N (12 carbon and 6 nitrogen atoms) and 12 graphene unit cells (24 carbon atoms), see Fig. 1. The optimized translational parameter was 8,47 Å and 8,48–8,49 Å for VASP and SIESTA calculations, respectively. In this work we considered the bilayer system without any tension, so the translation parameter optimization was performed by finding l , which corresponds to the minimum of the bilayer total energy E _tot( l ). The resulting parameter is ~0,9% smaller than that for a free isolated graphene monolayer (8,55–8,57 Å) and ~1,9% larger than that for a free isolated C 2 N monolayer (8,31–8,33 Å), calculated within the same approximations. Selected simulation parameters presented in Table 1 allowed us to obtain the interlayer binding energy with a precision of less than 0,25 meV/atom. More details about calculation parameters optimization can be found in [15]. The plane wave basis energy cutoff was 600 eV, for pseudo-atomic orbitals we used optimal parameters for C 2 N monolayer from [16] and for graphene from [17].

Table 1

Simulation parameters

DFT package	SIESTA	VASP
XC approximations	PBE+D2 BH-vdW	PBE+D2
k -points	19×19×1	15×15×1
Space partitioning (mesh detailing in the real space): MeshCutoff (SIESTA) / PREC (VASP)	360 Ry	Accurate
Total energy convergence criterion	10–6 eV
Force convergence criterion	5·10–5 Ry/Bohr (≈1,3 meV/Å)	10–3 eV/Å
Vacuum layer, Å	35

Interlayer binding energy was calculated as:

Ebind = E bilayer - E C-^N - E graphene - E CP ,                            (1)

where E_bilayer , E_CN , and E_graphene are the total energy of the bilayer, an isolated C 2 N monolayer, and an isolated graphene, respectively; E_CP is the Boys–Bernardi correction to the basis set superposition error [18]. For PW calculations this correction equals zero.

Geometry optimization with BSSE correction

Since BSSE for the basis of atomic-like orbitals results in the artificial attraction between layers, if we allow the system to relax without any constrictions, we will obtain too small layer separation. Therefore, to investigate the influence of BSSE on the bilayer geometry, we performed a series of calculations

Физика with the fixed interlayer distance for each considered basis set (optimized and default) and XC approximation. The distance was changed manually with 0,05 Å step (0,01 Å near the total energy minimum to determine the precision). The resulting dependencies of the bilayer total energy before and after taking into account Boys–Bernardi correction to BSSE on the layer separation are presented in Fig. 2.

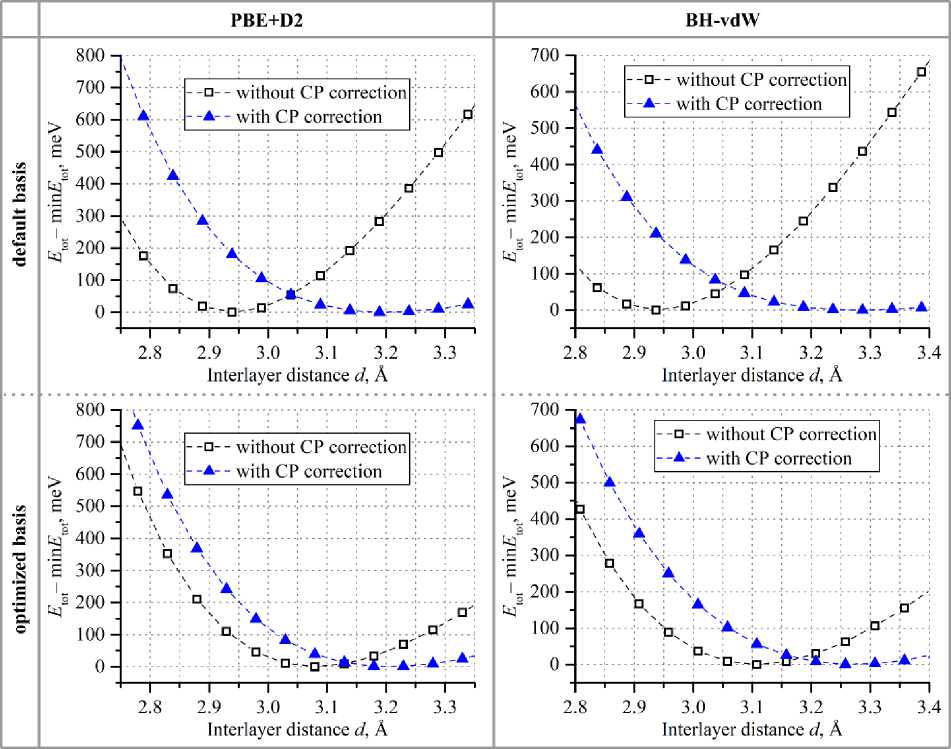
Fig. 2. Dependencies of the bilayer total energy on the interlayer distance for default and optimized PAOs in two XC approximations before and after BSSE corrections

Fig. 2 shows that, predictably, in all considered cases, BSSE corrections lead to the increased layer separations. Basis optimization allows us to obtain larger interlayer distances even before taking into account Boys–Bernardi correction to BSSE. Table 2 proves that basis optimization gives much closer to BSSE-corrected geometries (the layer separation difference between BSSE-corrected and not-corrected cases is two times smaller for optimized PAOs). However, BSSE correction diminishes the geometrical difference between structures obtained with optimal and default bases: BSSE-corrected layer separations are almost equal for each basis set. Moreover, this correction can be substantial, especially for default basis (BSSE-corrected interlayer distances are up to 12 % larger).

Table 2

Interlayer distance before ( d ) and after ( d BSSE ) taking into account Boys-Bernardi correction to BSSE

XC approximation	Basis	d BSSE   d , ^	( d BSSE   d ) / d , %
PBE+D2	default	0,27	9,0
	optimal	0,13	4,2
BH-vdW	default	0,35	11,9
	optimal	0,16	5,1

So, when subsystems are similar in size, unsurprisingly, BSSE correction considerably changes the weak-bonded system geometry (interlayer distance, in particular). Next, we will check the scale of this influence on the energetic properties and compare results with the BSSE-free plane-wave calculations.

BSSE influence on the C2N/graphene bilayer binding

The plane-wave calculations gave the following results: interlayer distance d = 3,18 Å; - E_bind = 646 meV (which is 26,9 meV per atom of graphene or 0,17 J/m²). Firstly, we compare them to the SIESTA results obtained with the same XC approximation (PBE+D2). The precision of interlayer distance calculations A d ® 0,02 A. In Table 3 we calculated AE and e as:

VASP      ^{d - d} VASP

^A E  E bind   E bind , ^e 3                                     (2)

dVASP where E and EVASP are binding energies calculated in SIESTA and VASP, respectively; the interlayer distances are similarly denoted.

Table 3 Binding energy and layer separation of the C 2 N/graphene bilayer before and after BSSE correction in geometry (calculations in PBE+D2 XC approximation)
Basis	not BSSE-corrected geometry					BSSE-corrected geometry
	—Ek i bind , meV/atom (J/m2)	ECP , meV/atom	∆ E , meV/atom	d , Å	e , %	—Ek 1 bind , meV/atom (J/m2)	ECP , meV/atom	∆ E , meV/atom	d , Å	e , %
default	11,6 (0,07)	94,6	–15,3	2,94	–7,6	19,1 (0,12)	93,6	–7,8	3,21	0,8
optimal	26,8 (0,16)	32,2	–0,1	3,08	–3,1	28,4 (0,17)	28,3	1,5	3,21	0,8

Table 3 shows that BSSE correction in geometry gave close to plane wave interlayer distances even for default basis (relative deviation e drops from almost 8 % to less than 1 %, and the resulting layer separations are equal for optimal and default bases). However, basis optimization is critical if the correct interlayer binding energy is needed. The Boys–Bernardi correction could amount to almost 90 % of raw binding energy before BSSE correction (for default basis set before taking into account BSSE in geometry). For optimal basis, E_CP drastically diminishes (by 3 times in comparison to default basis) and now is about the value of binding energy. Therefore, if atomic orbitals are used for simulations of weakly bonded systems it is critical to consider BSSE correction to the binding energy, otherwise, the binding could be significantly overestimated. Overall, E calculated with the optimized basis set are close to the VASP values, the difference is only ~1 meV per graphene atom. So, sound results could be obtained with the optimal basis set even before the BSSE correction in geometry.

Table 4

Binding energy and layer separation of C 2 N/graphene bilayer before and after BSSE correction in geometry (calculations in PBE+D2 XC approximation)

Basis	not BSSE-corrected geometry			BSSE-corrected geometry
	—Ek i bind , meV/atom (J/m2)	ECP , meV/atom	d , Å	—Ek i bind , meV/atom (J/m2)	ECP , meV/atom	d , Å
default	13,6 (0,08)	110,6	2,94	22,4 (0,14)	92,5	3,29
optimal	32,8 (0,20)	34,2	3,11	35,1 (0,22)	28,9	3,27

In the next step, we investigated how the choice of XC approximation will affect the BSSE value. The calculated results for the van der Waals functional are presented in Table 4. Similarly to the semi-empirical Grimme corrections, BSSE plays a huge role in the case of the default basis set. While BSSE-

Физика corrected geometries in both basis sets had similar layer separations, the default basis predicted considerably weaker binding. The optimized basis set gave closer values of binding energy to the planewave calculations with a similar XC functional [19]. Overall, the interlayer binding energy calculated with both XC functionals suggests a weak interaction. Obtained values are close to the binding energies of graphite layers [20].

Conclusion

Here, we obtained the optimized model of the C2N/graphene bilayer. We investigated its structure and interlayer binding using the electron density functional method implemented in codes with two approaches to wave function decomposition (VASP and SIESTA packages). We considered the influence of PAOs optimization and BSSE correction on the results of interlayer binding energy and distance calculations.

We showed that to obtain the correct energetic and structural properties of the bilayer it is necessary to optimize the atomic-like basis set and use the counter-poise correction to BSSE during the calculation of both interlayer binding energy and layer separation. BSSE-corrected results calculated in optimized pseudoatomic orbitals are in agreement with plane wave simulations. For PAOs, we showed that for a weakly bonded system with almost equal sub-systems, it is essential to take into account BSSE correction, otherwise, the binding energies will be highly overestimated (by 45–90 %). Overall, both XC approximation predicted similar interlayer binding energies, which lie in the range of van der Waals bonding.

The reported study utilized the supercomputer resources of South Ural State University [21].