Efficiency of parallel computations of gravitational forces by treecode method in n-body models

DOI:

The N -body model is used to simulate the dynamics of galactic systems, including open clusters and globular clusters [4; 12], single galaxies, interacting galaxies, groups and clusters of galaxies [1; 2; 6; 9; 14; 15; 19; 23; 32; 33]. There are a significant number of numerical algorithms for parallel implementation of methods for calculating gravitational forces in N -body system. The simplest direct summation method of each particle to each other one (Particle-Particle, PP) greatly limits the number of particles due to the complexity of O(N 2 ) , although it can serve as a tool for testing [9]. The algorithm proposed in [3] based on a special partitioning of the volume with particles is traditionally called TreeCode. It reduces the complexity of calculations to O(N log(N)) by reducing the accuracy of the contribution to gravity from distant particles.

A variety of fast methods for calculating the gravitational force in a system of N particles have been proposed over the past decades. We highlight such methods as Fast Fourier Transform (FFT) with complexity close to O(N log(N)) , Particle-Mesh Method, Particle-Particle + Particle-Mesh ( P ³ M ) and others [2; 20; 35]. The FFT method has a number of advantages for simulating modified gravity [27]. A special feature of the Grid-of-Oct-Trees-Particle-Mesh (GOTPM) algorithm is a hybrid scheme combining particle-mesh (PM) and oct-trees of Barnes-Hut method [7; 21]. A generalization of tree codes is Fast Multipole Method with number of computational operations O(N ) [2; 36].

Large cosmological simulations projects aim to study the cosmological evolution of dark and baryonic matter, as well as the physics of galaxy clusters over 10 10 years based on N -body and/or hydrodynamical simulations [26; 34]. Examples of such projects are Mil-lenniumTNG (3000-megaparsec box with more than 1 trillion particles) [11], PKDGRAV3 ( N = 8 • 10 ¹² ) [26], EAGLE simulation (Evolution and Assembly of GaLaxies and their Environments) [28], FLAMINGO project [29], Illustris-TNG [25] and many others.

The use of cosmological models has proven its effectiveness in solving problems of the dynamics of single galaxies or galaxy groups, as in the Auriga project [10] and the Apostle project [8]. The use of high-order parallel N -body codes for GPUs allows one to study the dynamics of globular clusters [13] and compact elliptical galaxies on cosmological time scale [15].

The number of real stars in galaxies is always much larger than the number of particles in the model, and this requires the fulfillment of the collisionless condition of the stellar component in the simulations [17; 30]. Various approaches have been proposed to improve the quality of N -body models. An example is the GalaxyFlow, which aims to create a method to go from very coarse stellar phase-space density in the original numerical simulations to more accurate stellar phase-space density estimates for astronomical applications [22].

The aim of the work is to calculate the efficiency of parallel N -body simulations based on TreeCode. Since the bottleneck of the Message Passing Interface is the speed of data exchange between processors, our analysis is limited to the OpenMP standard within the shared memory. Processors have both physical cores (processor cores) and extra threads (virtual or logical cores) thanks to Hyper-Threading Technology. We present the details of our analysis of the performance of Treecode for calculating gravitational forces using extra threads in addition to the processor cores.

1.    N-body simulation with TreeCode

The dynamics of N gravitating particles is described by a system of equations dri

= v i , dt

A dviV^

—— = > Gm-dt^

-r'

^r J

-

Г '

r -

-

r, | ² + e^ ’

where r _i; V ' and m ' are the radius vector, velocity and mass of the г -th particle, respectively, G is the gravitational constant, e is the smoothing radius that gives a collisionless system. The dynamical N -body model includes only a stellar disc and lacks a dark halo defined by a given gravitational potential, as in [5]. The initial equilibrium in the rotating disc is provided by the balance of gravitational and centrifugal forces with an additional contribution from random particle motion, which is described by spatial distributions of velocity dispersions in three directions [9; 15; 16; 24]. The dispersion of the random velocity component along the vertical coordinate is an analogue of pressure and compensates for the gravitational force, which gives an equilibrium disk in the transverse direction.

The numerical integration of the system (1) is based on the classical second-order

leap-frog scheme: v”+1/2 = v” + T ai*’                                 (2) r”+1 = r” + т v”+1/2’                                 (3) a"+1 = a(r"+1)’                                      (4) v”+1 = v      + Т ai*+1,                               (5) where т is the time step, a” is the acceleration of the г-th particle, index n corresponds to the time tn.

Direct summation in the formula (1) for each particle of the contributions from all other bodies (Particle-Particle, PP method) yields a computational complexity of O(N ² ) . The quadratic dependence of the computational time on the number of particles greatly limits such a naive approach. However, the direct method has a number of advantages. Obviously, the calculation error for PP is minimal compared to approximate algorithms for the same N , which provides a significant advantage for satisfying the physical conservation laws [16; 18]. This allows for a higher-quality reproduction of the evolution of a gravitating system over large times and small scales, which is especially important for the gas component with large mass density gradients [15].

The calculation of gravitational forces in (1) is performed by the TreeCode method [3], based on the idea of an approximate construction of the gravitational potential of “distant” particles group. The contribution of such a group is calculated as for one particle with the total mass of the entire group, located at the center of mass. The contribution of “near” particles is calculated by an exact formula. The implementation of this approach is based on a hierarchical partitioning of the space into eight octants until there is no more than one particle left in each subdomain. The division into “near” and “distant” groups is determined by the value of the parameter θ. It has the meaning of the solid angle at which a given subdomain is visible from the point under consideration. This method has an algorithmic complexity O(N log(^)) . The TreeCode method turns into a direct method PP for calculating accelerations with algorithmic complexity O(N 2 ) for 0 ^ 0 .

The key problem is the choice of the criterion when the group of particles is distant [2; 31]. Since the tree code characteristics, the errors in calculating the gravitational forces and the features of the spatial distribution of particles are interconnected.

Calculating gravitational forces takes up the lion’s share of the processor time regardless of the method of numerical integration of the equations system. Using the TreeCode method in this work requires over 95 percent of the time to calculate accelerations. This value varies within 2 — 3 percent depending on the choice of the computing system.

2.    Code performance analysis

We use the FORTRAN-77 version of TreeCode ² adapted for galactic stellar disc dynamics simulations [9]. This code is parallelized using OpenMP technology.

Using the compiler gfortran 12.2.0 with the optimization switch -O3 provides the most complete optimization in terms of execution time without specific extensions of the instruction set architecture (ISA) of the target processor. Aggressive optimization methods are not used, since they may affect the numerical results, such as option -ffast-math , which allows deviations from strict compliance with the floating-point number representation standard IEEE 754, for example, in the case of subnormal numbers and the implementation of associativity of computations. This choice is due to the fact that we focused on the study of quantitative characteristics associated with parallel computing and do not consider a specific processor instruction set architecture. Solving mathematical simulation problems makes it preferable to use specific extensions of the instruction set of the target processor (the SSE family of extensions of various versions, AVX, etc.) using switch -march=native , which allows using all available instructions supported by the processor and the compiler.

We calculate the following characteristics of software parallelization performance: dependencies of the execution time of one step of the computational cycle T (Time), the computations speedup S (Speedup) and the efficiency of parallelization E (Efficiency) on the number of threads used M. The definitions of these quantities are чал - Tf1)        - S(M)

S(M) = TM ’ E(M’ = ^’ where E is the efficiency without extra threads.

The parameters T, S, and E are measured on several different shared-memory computers (symmetric multiprocessing, SMP), the parameters of which are shown in Table 1. It is important to note that the processors are capable of dynamically changing the clock frequency depending on the current computing load level (Intel Turbo Boost and AMD Precision Boost technologies). Additionally, there is the ability to execute two logical computing threads on one physical processor core (Hyper-Threading Technology). The total number of available computing threads M = Mp + Me consists of physical cores Mp and additional logical computing threads (extra threads) Me. We compare two types of CPUs, both with support for hyper-threading technology (Me = Mp, M = 2MP) and without it (Me = 0, M = MP). Thus, threads on a single CPU may be nonequivalent, which is almost always a problem for a parallel program. Formulas for E(M) in the form (6) are traditionally used for M < MP. The efficiency in the case of M > MP (Me < 1) should be written in the form

E < p \M ) = ^SM1 ^v ’    M_P

T (1)

T(M ) M _P ’

since only physical cores must be considered, M _P = M — M _e .

All results were obtained for averaged values of execution time of one step of the computational cycle T . Averaging was performed over ten steps of time integration. Therefore, we plot absolute errors in the figures as vertical bars. Measurement errors were calculated by using the following expression of standard error of the mean:

A(T ) =

AAATT—TA у     n(n — 1)     ’

where ( T ) is the mean value of T , n = 10 is the number of measurements. The corresponding errors of S and E have larger values because they are calculated as ratios of A/B , which gives

* (B) =

A • A(B) + B • A(A) B ²

The main parameter determining the accuracy of the gravitational force calculation in the TreeCode algorithm is the opening angle θ. This free parameter actually specifies the hierarchical structure of the grid on which the gravitational potential is calculated. All numerical experiments in this work are carried out for 0 = 1 . This choice is typical in the practice of N -body simulations. Reducing 0 greatly increases the time T , all other things being equal. There is a transition from TreeCode to PP in the limit 0 ^ 0 .

The results of calculating the average time T , speedup S and efficiency E ^{( P} ) for different computing systems and the number of threads M are shown in figures 1-8. The simulation time T consists of the execution time of the following components of the algorithm in accordance with formulas (2)–(5): calculating gravitational forces for a system of N particles ( T ^{( grav )} ), determining velocities at the predictor stage ( T ^{( v 1)} ), new coordinates ( T ^{( r )} ), velocities at the corrector stage ( T ^{( v 2)} ) and accelerations ( T ^{( a )} ) of particles. Since T ⁽₉rav) /(T (grav) _{+ T} ( v i) ₊ t ( ^r ) ₊ t ^{( v 2)} + T ^{( a )} ) ~ 0.96 , we restrict ourselves to the approximation T = T ^{( grav )} below.

Characteristics of computing systems

Table 1

Name	CPU	Total number of cores (number of      logical threads)	RAM	CPU    release date
Beta	2 x Intel Xeon E5405, 2 GHz	8 (8)	16 GB DDR2-667	2007
Epsilon	2 x Intel Xeon E5540, 2.53 GHz	8 (16)	16 GB DDR3-1600	2009
K80	2      x      Intel     Xeon E5-2687W v3, 3.1 GHz (3.5 GHz with Turbo Boost)	20 (40)	512 GB DDR3-2133	2014
M105	Intel Core i5-6400, 2.7 GHz (3.3 GHz with Turbo Boost)	4 (4)	8 GB DDR3-1600	2015
M111	Intel Core i5-9400, 2.9 GHz (4.1 GHz with Turbo Boost)	6 (6)	16 GB DDR4-2666	2019
M113	12th Gen Intel Core i5-12400F 2.5 GHz (4.4 GHz with Turbo Boost)	6 (12)	16 GB DDR5-5200	2022
M105S	Intel Core i9-9900KF 3.6 GHz (5.0 GHz with Turbo Boost)	8 (16)	64 GB DDR4-2400	2019
M301	2 x Intel Xeon E5-2630 v3, 2.4 GHz (3.2 GHz with Turbo Boost)	16 (32)	16 GB DDR4-1866	2014
Ryzen	AMD Ryzen 7 2700, 3.2 GHz (4.1 GHz with Precision Boost)	8 (16)	16 GB DDR4-3200	2018

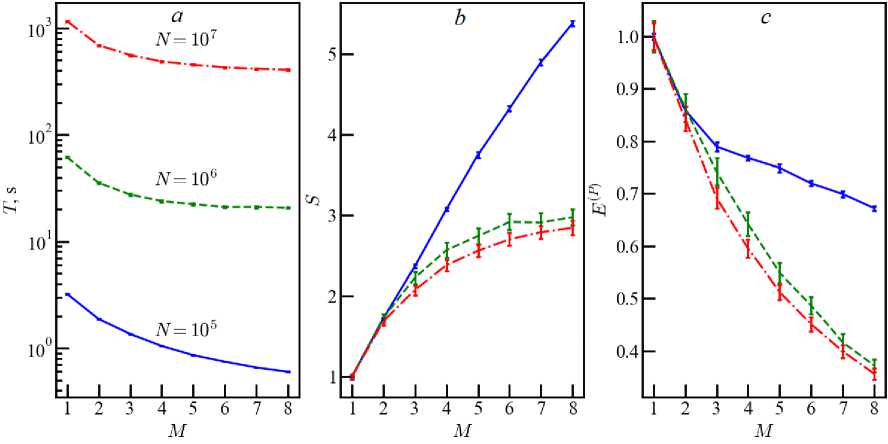
Fig. 1. Computational time ( a ), speedup (b) and efficiency (c) for computer Beta in simulations with different numbers of particles: N = 10 5 (blue), N = 10 6 (green), N = 10 7 (red)

Fig. 2. The same as in figure 1 for computer M105

Computer Beta has two processors with four physical cores each, which gives M p = 8 and M e = 0 . The dependencies T(M ) , S(M ) , E ^{( p} ) (M ) for the models with TV = 10 ⁵ , N = 10 ⁶ and N = 10 ⁷ are shown in figure 1. The computation time T decreases noticeably with the increase of the number of cores M for N = 10 ⁵ . Experiments with N = 10 ⁶ and N = 10 ⁷ give a slower decrease with an exit to an almost constant level. This, respectively, affects the speedup S(M ) and the efficiency E ^{( p} \M ) . The speedup reaches a plateau at M ^ 8 , in contrast to the simulation with N = 10 ⁵ with an almost linear increase in speedup. The efficiency turns out to be worse than 0.4 when using all available physical cores in models with N >  10 ⁶ .

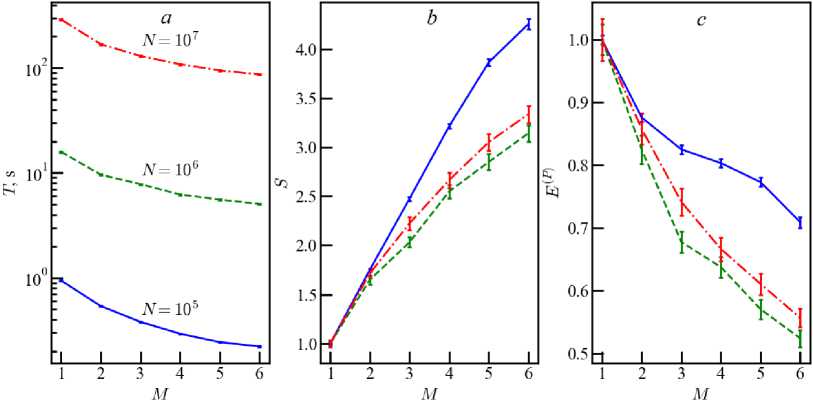
Fig. 3. The same as in figure 1 for computer M111

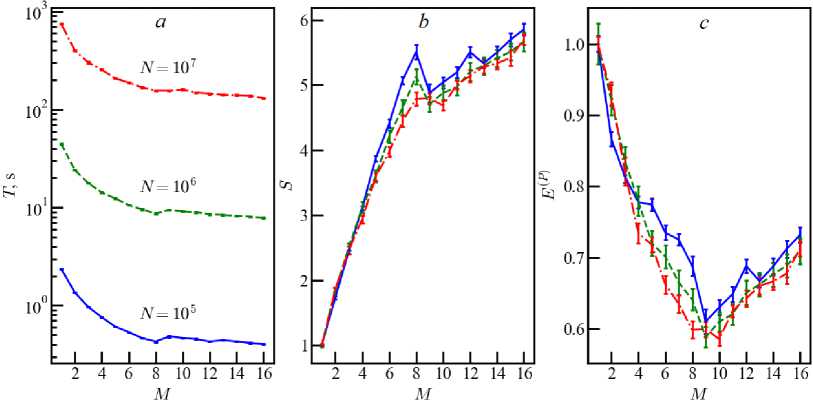
Fig. 4. The same as in figure 1 for computer Epsilon

Other processors without extra threads ( M _E = 0 ) have similar dependences of characteristics on the number of cores. The M105 processor is more modern and has a higher clock frequency than Beta. Therefore, the value of T on computer M105 is approximately 3 times less than on Beta (figure 2). However, the speedup and efficiency are better only within 10–15%. Such results are also preserved for the more modern processor of M111 in figure 3. Moreover, the growth of speedup continues to the maximum value of M p = 6 . There are higher speedups and efficiency for N > 10 7 in contrast to computer Beta due to the more modern architecture.

Next, we consider computing systems with ME = Mp, which doubles the number of threads. Computer Epsilon has 8 additional logical threads and M = 16. The value of T(M = 1) decreases compared to Beta due to the more advanced processor architecture (figure 4). Using only physical cores (M < 8) is more efficient for Epsilon than in the case of Beta. The dependences of speedup and efficiency on the number of particles are significantly weakened (figure 4). The difference in results for all three experiments with N = 105, N = 106 and N = 107 is small. All dependencies change sharply for the number of threads M > 8 when using extra threads. Two characteristic features stand out in parallel computing with M > Mp = 8.

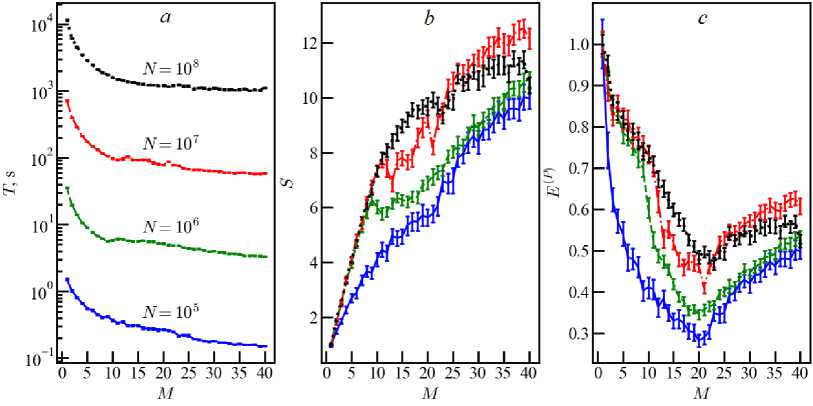
Fig. 5. The same as in figure 1 for computer K80

First, adding several extra threads leads to a noticeable decrease in speedup and efficiency. For example, using extra threads with M _E = 1 — 2 increases the time T compared to M = M _p = 8 (see figure 4 a ). Characteristic kinks in the dependencies S(M ) and E ^{( p} ) (M) in the vicinity of M = M _p = 8 show the negative impact of a small number of extra threads on the overall efficiency of simulations. The second feature appears when using the maximum possible number of extra threads. Such a doubling of the number of threads to M =16 allows exceeding the indicators with M = M _p = 8 . Comparing the efficiencies of E ^{( p} ) (8) and E ^{( p} ) (16) yields an increase of 6 percent for N = 10 ⁵ and 19 percent for N = 10 ⁷ for computer Epsilon.

The nature of the dependencies T(M ) , S(M ) , E ^{( p} ) (M) for M < 8 for computer Epsilon (see figure 4) is due to the fact that one logical computing thread is used on one physical processor core. A further increase in threads ( M >  8 ) leads to the use of two threads on one core, which violates the monotonic dependence. Computer Beta does not have extra threads ( M = M _p ), which gives monotonicity of efficiency (see figure 1).

Next, we consider computer K80 (see Table 1), including an additional model with N = 10 ⁸ , which requires more RAM ( ^ 6 GB). The total number of threads reaches M = 40 for M _p = 20 and M _E = 20 . K80 contains 2 processors with shared memory. Figure 5 shows our results for K80. There are peculiarities when the number of threads passes near M ~ 10 and M = M _p = 20 . The first is due to the two processors on K80. The transition from M =10 to a higher number of threads means either using the second processor or/and partial calculations on extra threads of the first or second processor. The choice of a specific operating mode is determined by the operating system and is not adjustable by the user.

The internal scheduler does not provide information on the distribution of resources between devices. However, the dependencies T(M), S(M), E(p)(M) allow us to assume that the distribution of computing resources occurs as follows. At the beginning, one logical computing thread is allocated to one physical core of the first processor (M < 10). Then the second threads are added to each core of the first processor (10 < M < 20). The next stage begins with the use of the second processor (20 < M < 40). This transition is especially noticeable for a very large number of particles in models with M < Mp (see figure 5). Comparing the efficiencies of E(p)(20) and E(p)(40) yields an increase of 77 percent for N = 105 and 8 percent for N = 108 for computer K80.

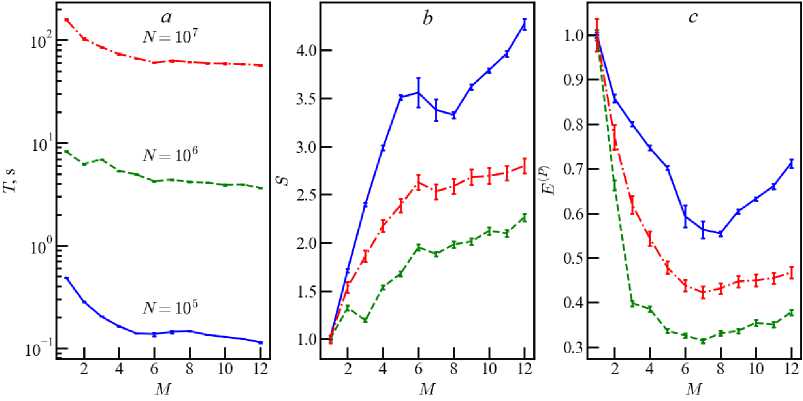
Fig. 6. The same as in figure 1 for computer M113

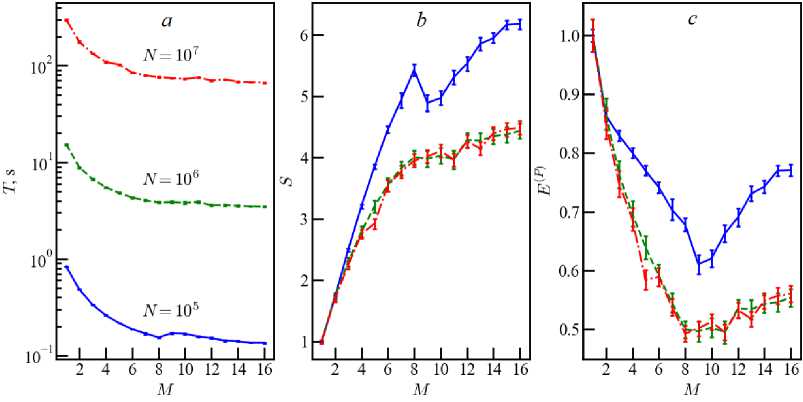
Fig. 7. The same as in figure 1 for computer M105S

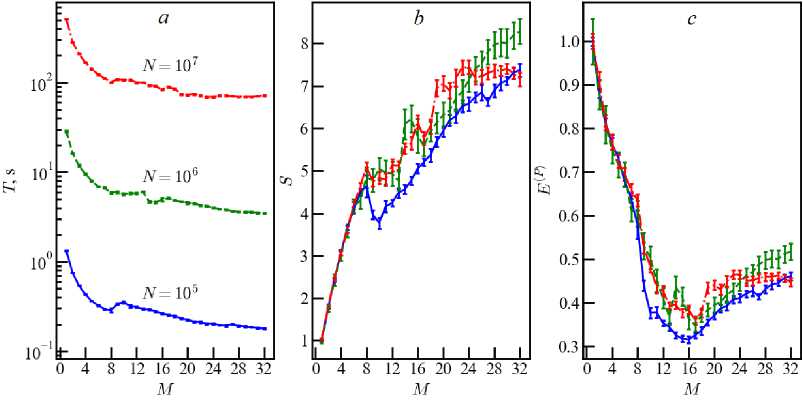
Fig. 8. The same as in figure 1 for computer M301

Figures 6–8 show the result of the efficiency calculation for systems with extra threads, as a continuation of the analysis for Epsilon and K80. The transition of the number of threads through M = M p remains critically important. Comparison of E ^{( p} ) (8) and E ^{( p} ) (16) for computer M105S gives a gain about of 12 percent when using the maximum number of extra threads. The result for computer M301is shown in figure 8, which demonstrates a slightly different version of resource distribution among threads. We have a characteristic kink in the dependencies near M = M _p /2 = 8 . This means that extra threads begin to be used, although there are still free physical cores. At the same time, using the maximum possible number of extra threads for the M301 processor also improves the efficiency of parallel code about by 40 percent in models with ( N ~ 10 ⁵ - 10 ⁶ ).

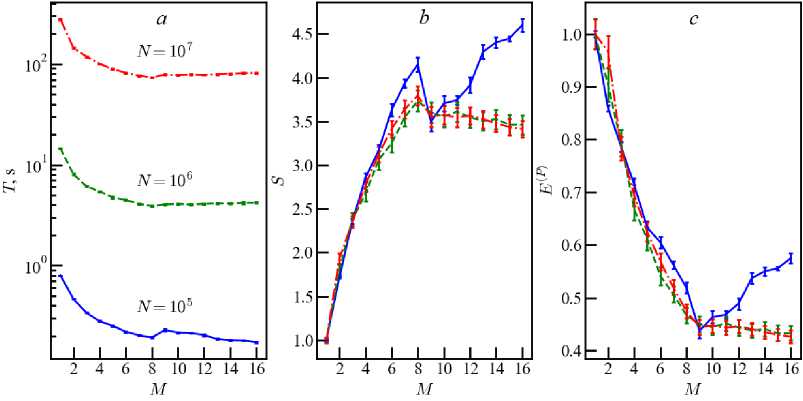
Fig. 9. The same as in figure 1 for computer Ryzen

Computer Ryzen is based on AMD processor. The result of calculating T(M ) , S(M ) , E ^{( p} ) (M) differs from the CPUs considered above (figure 9). Only models with a small number of particles reproduce similar dependencies. Extra threads for models with N > 10 ⁶

do not provide a performance boost, worsening the result for any number of M _E . Whether this conclusion is general for AMD processors or applies to a specific CPU requires further study.

Figure 10 shows the dependence of the program execution time on the processor release year from our sample. These results illustrate Moore’s law. We have an approximately exponential decrease of the form T a 2^-t /^{T y} with т _у = 5.6 years for the model with N = 10 6 and M =1 (see the black dashed line in figure 10). There is a noticeable spread of the time scale r ₉ within 5-6 years for different models. The general trend of the data in figure 10 fits into the historical development of computing technology.

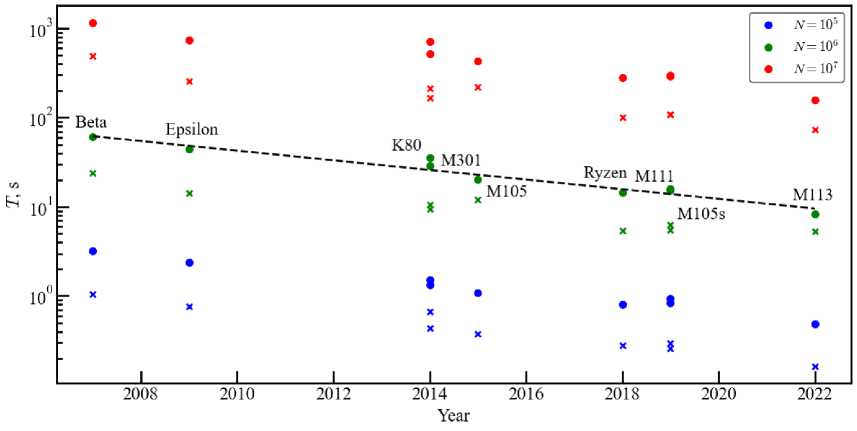
Fig. 10. The execution time of one integration step on one core (M = 1 , circles) and four cores ( M = 4 , crosses) from the processor release date for various computers from Table 1 in models with N = 10 5 (blue), N = 10 6 (green) and N = 10 7 (red). The black dashed line represents the approximation T a 2 ^{- t/ T} » with r ₉ = 5 . 6 years

The results discussed above are based on three main models with the number of particles N = 10 5 ; 10 6 ; 10 7 . Figure 11 shows in more detail the dependencies of the efficiency E on the number of particles in the range 2 17 < N < 2 24 . We restrict ourselves to the number of physical cores M = M _P = 4 and M _E = 0 in order to conveniently compare and cover all processors from Table 1. Models with a small number of particles demonstrate a small spread of efficiency within 0.67 — 0.81 . Simulations with N = 2 24 ~ 1.7 • 10 7 give a spread of E = 0.45 — 0.85 . An increase in N can lead to both a decrease and an increase in efficiency, which is manifested in the non-monotonic behavior of the dependencies E ^{( P} ) (N) in some models. Such a result was noted, for example, in simulations on GPU with CUDA for a similar model [16].

This effect can be caused by uneven distribution of data across RAM modules and dual-channel access to it. An important factor is also the ratio between the processor data processing speed (P) and RAM bandwidth (R), P/R. Let’s consider two scenarios, in each of which all data are physically located in one RAM module with small N. The first case corresponds to the condition P/R > 1. Then the computation efficiency will grow with increasing N until it reaches a certain value Ncrit, after which it will begin to decrease. Further growth of N requires placing data in two memory modules, which allows using the second access channel to it and leads to some increase in efficiency with a further plateau. The opposite inequality P/R < 1 determines the second option, when the condition N > Ncrit is satisfied immediately. The growth of N is accompanied by some decrease in efficiency until the data is physically placed in two different memory modules. This allows the second channel to be used and the efficiency to increase slightly, reaching a plateau, as in the first case.

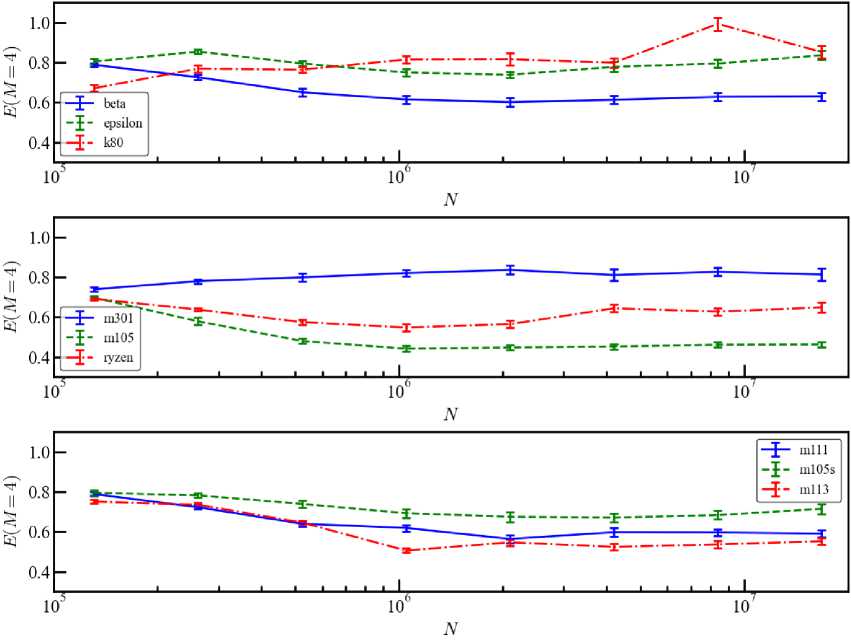
Fig. 11. Dependence of efficiency on the number of particles for four computational threads for different processors

Conclusion and discussion

The analysis of the efficiency of parallel implementation of the code for calculating the gravitational force was performed for a system of N particles using the Treecode method. We limited ourselves to considering the Open Multi-Processing (OpenMP) standard, since the use of the Message Passing Interface (MPI) for calculations on several processors significantly depends on the characteristics of the communication network.

Speedup and efficiency of parallel simulations depend on a large number of subtle factors that determine the architecture of multi-core processors. We focus on the role of additional logical threads (extra threads) that change the efficiency of executing parallel codes. Our results show that increasing the total number of threads due to extra threads (ME) improves the efficiency of parallel Treecode calculations to an average 20 percent for different processors only in the case of ME = Mp. If the number of extra threads is less than the number of physical cores, then the use of logical threads can significantly worsen the efficiency of parallelization.

A significant negative factor is the special reduction of the processor frequency in multi-core processors. The presence of a base frequency v ⁽¹⁾ and a frequency in the Boost mode v ⁽²⁾ leads to calculations with a changing processor frequency. The transition from v ⁽¹⁾ to v ⁽²⁾ can occur in several steps, since the processor frequency is adjusted to the current load. If the computer has several processors with shared memory, this can unbalance the efficiency of parallelization.

Note the emergence of processors with a new architecture, which have a more extensive set of cores. An example is processor Intel Core i9 14900K, which allows the use of 32 threads. The cores are divided into 8 performance cores (P-core) and 16 efficient cores (E-core). Performance cores support 8 extra threads, which gives a total number of threads M = 32 . The question of the efficiency of such processors with a more complex architecture requires a separate analysis.

NOTES

• ¹    This work supported by the Russian Science Foundation (grant no. 23-71-00016, https://rscf.ru/project/23-71-00016/ ).

• ²     https://home.ifa.hawaii.edu/users/barnes/treecode_old/index.html