Efficient clustering algorithm with enhanced cohesive quality clusters

Published Online July 2018 in MECS

For above reasons, this paper proposes efficient clustering algorithm using spectral analysis, domain knowledge, and split-merge-refine approach. This enhances the efficiency, quality and minimizes empty clusters. The performance of this algorithm is checked on 10 real small to large data sets. This paper is organized as follows: Section II summarizes literature surveys and related work from the year 1999 to 2017. Section III describes the working of some standard clustering algorithms from all the above categories. Section IV covers the proposed clustering algorithms. Section V covers experimental results analysis of standard and proposed clustering algorithms on various data sets using validity measures. Section VI covers conclusion and future work of this paper.

• II.    Related Work

One of the simple efficient filtering algorithms is Lloyd’s k-means clustering. The implementation of this algorithm is easy because it uses k-dimensional tree data structure for data clustering. But this algorithm can be improved further [1]. The appropriate value of k and initial selection plays a vital role in improving the quality of clusters. In order to overcome these problems associated with the initial selection, the new greedy initialization method is used. These select suitable initial centroids to form more compact and separated clusters [2]. This new method takes more time to search centroids. The distance measures play a vital role in the process of clustering. New distance measure along with new clustering algorithm which is based on the k-means algorithm is known as the circular k-means [3]. This algorithm is used to cluster the vectors of directional information. Selecting the appropriate value of k is difficult for clustering. Also, checking the validity of final clusters is challenging. For these two reasons, validity measures are useful. Nine validity measures based on a property of symmetry are used to estimate the value of k and validity of clusters. These measures include Davies–Bouldin, Dunn index, Point symmetry, I, Xie–Beni, FS, K, and SV index [4]. One of the popular clustering algorithms is k-means. For the k-mean, the user needs to give the value of k and initial centroids, which affects the overall quality of clusters. Also, results of k-means may be affected by noise in data. Density based noise detection can be used to filter noise. This helps in getting more accurate results [5].

Authors propose [27] method to optimize a number of clusters k, with minimum time complexity. This reduces the effort required for each iteration by decreasing reclustering of data objects. The different distance measures are used to track the effect on the computational time required per iteration. Therefore, this algorithm may produce less reliable clusters of data objects [28]. This paper presents enhanced method to select k and initial centers using weighted mean. This method is better in terms of mathematical computation and reliability. The performance of the standard k-means algorithm will be affected by the selection of the initial centers and converges to local minimum problems [29]. This paper proposes a new algorithm for initialization of the k-means to converge into a better local and also to produce better clusters.

From the above literature, it is observed that very few papers are focusing on all the aspects related to enhancement in a single algorithm. Hence, this paper is integrating more than two features in the single algorithm.

• III.    Candidate Clustering Algorithms

As per the above literature, clustering algorithms are partition, hierarchical, density, grids and model based. In each of the above categories, some candidate clustering algorithms are studied in this section. This paper studies algorithm from various categories analyzes their strong and weak points. This is done by applying and measuring performance on various data sets from the kaggle with various validity measures. Then these algorithms can be used to compare with the proposed efficient clustering algorithm. The summary of these clustering algorithms with their basic steps and their strong and weak points are given as follows:

• A.    k-Means Clustering

The k-means belongs to partition based clustering. Inputs for k-means are a number of clusters and it selects initial centroids randomly. The algorithm is divided into following three steps:

• 1.    Read data and value of k.

• 2.    Data assignment steps using distance measures.

• 3.    Updating centroids and clusters.

• 4.    Forming final clusters.

The value of k should be provided at the beginning of clustering. Poor qualities clusters are generated because initial centroids are selected randomly.

This algorithm can be used for the numerical type of data.

Quality can be improved further.

• C.    The Balanced Iterative Reducing and Clustering using Hierarchies

BIRC or Balanced Iterative Reducing and Clustering using Hierarchies is the example of the hierarchical type of clustering algorithm [44]. This algorithm constructs clustering features tree from data and leaf nodes are clustered. Steps of this algorithm are as follows:

• 1.    Scans the data sets to construct features tree.

• 2.    Apply the clustering to cluster the leaf nodes.

The quality of clusters generated by the BIRC is not good.

• D.    The Clustering Using Representatives

CURE or Clustering Using Representatives is the example of the hierarchical type of clustering algorithm [44]. Steps of this algorithm are as follows:

• 1.    Read data sets and create the p partitioned.

• 2.    create the representative points for k clusters.

CURE has a high run time complexity for big data.

• E.    The Density Based Spatial Clustering of Applications with Noise

DBSCAN or Density Based Spatial Clustering of Applications with Noise belongs to density clustering algorithm. For this algorithm, the user has to provide minimum points and radius. Steps of this algorithm are as follows:

• 1.    Select any data objects as a unvisited point.

• 2.    Identify the neighborhoods of the point.

• 3.    Clusters the points

• 4.    Identify the other unvisited.

This algorithm is only applicable for the specific type of data sets.

• F.    CLIQUE Clustering

It is grid based type algorithm of clustering used to find subspace clusters of data sets. This algorithm is divided into following steps:

• 1.    Finding the dense area of data sets.

• 2.    Generate the k-dimensional cells.

• 3.    Eliminates the low-density cells.

• 4.    Cluster the high-density cells.

It is necessary to give more parameters to work correctly.

• G.    Expectation Maximization

EM or Expectation Maximization is standard model based approach to clustering. This algorithm is divided into following steps:

• 1.    Assigning the each data objects hypothetically to one of the clusters.

• 2.    Update the hypothesis and assign data objects to new clusters.

EM takes more running time for to cluster the data sets.

• IV.    Proposed Efficient Clustering Algorithm

From surveys of modified and standard methods of the clustering algorithm, this paper presents efficient clustering algorithm with following features.

• 1.    It is uses improved k-means clustering algorithm [21] to automatically predict the value of a number of clusters and appropriate initial centroids.

• 2.    This algorithm is making use of split and merges technique to clusters large data.

• 3.    This algorithm also removes the empty clusters.

• 4.    Refinement step is added to form more cohesive clusters.

• 5.    The algorithm is more efficient and produces high-quality clusters.

This algorithm consists of following three major steps:

• 1.    Predicting value of k and initial centroids using domain knowledge and spectral analysis[19][21]

• 2.    Forming the intermediate clusters.

• 3.    Refining the clusters to form final clusters.

Fig.1 shows the flow of proposed algorithm.

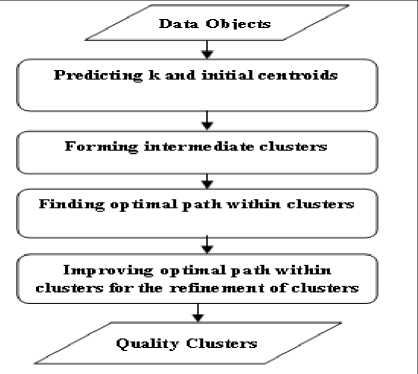
Fig.1. Flow of Proposed Algorithm

Detailed algorithm is given as follows:

Input: Data Objects

Output: Quality k-Clusters

Phase 1: Predicting k and initial centroids

• 1.    Scan the input data and estimate the value of k by understanding and analyzing properties of data objects using domain knowledge and spectral analysis.

• 2.    Select only required attributes of data from the data sets using above analysis.

• 3.    Use improved clustering algorithm to determine initial centroids and form the clusters.

Phase 2: Forming intermediate clusters

• 1.    Check if the k is sufficient to apply fine tuning, if yes, fine tune k by reducing it.

• 2.    Find the cluster with maximum negative impact, i.e., maximum within-SS.

• 3.    Split the cluster into 2 new clusters and replace it in the list of clusters.

• 4.    Calculate the accuracy of the newly formed clusters.

• 5.    Repeat steps 2, 3 and 4 until the accuracy is

• 6.    If the new accuracy has no significant improvement, consider the previous instance of clusters list as the final clusters.

• 7.    Create clusters using above methods.

significantly increasing.

Phase 3: Improving and finding optimal path within clusters for the refinement of clusters

• 1.    Identify outliers and form them into one cluster.

• 2.    Reduce the clusters by eliminating empty clusters.

  • 1.1.    Scan all the clusters and for each cluster check if there exist some points in it.

  • 1.2.    If for any cluster number of point is zero, then remove the cluster and reduce the value of k by one.

• 3.    Take all the formed clusters.

• 4.    For every element in the cluster ‘A’:

• 1.    Take element of this cluster A_i

• 2.    For every element in the other cluster ‘B’:

• 1.    Take the distance

• 2.    Store this distance in Distances [] Array.

• 5.    The minimum (Distances []) is the distance between cluster A and B.

• 6.    Store this minimum distance between these two clusters.

• 7.    Repeat steps 2, 3 and 4 for all cluster pairs

• 8.    Find out the cluster pair with a minimum distance between each other, say pair P.

• 9.    Merge these clusters and calculate new accuracy.

• 10.    Repeat this until the accuracy significantly increases.

• 11.    If the new accuracy has no significant improvement, consider the previous instance of clusters list as the final clusters.

• 12.    Stop when criteria met.

D = ( A - B )2               (1)

possible.

In this algorithm, there are three phases. The first phase predicts the value of k and initial centroids. The second phase uses split and merges techniques to form intermediate clusters based on predicted value of k. And the third step is responsible for refining the clusters with no empty clusters and high cohesive clusters.

• V.    Experimental Results

The clustering algorithms[25] such as k-means, PAM, Hierarchical clustering, DBSCAN and proposed clustering algorithms are applied to various data sets. Also proposed algorithm is compared with R-k-means clustering which uses Lloyd’s algorithm. And then comparative experimental results are presented in this section. For the experiments, this paper is using the accuracy of clustering, running time of algorithms, silhouette, Dunn, DB and CH scores to compare the performance of algorithms. Details of these measures are given in paper [4][13][40]. The value of accuracy, Silhouette, Dunn, and CH should be high whereas the value of running time and DB index should be low for better clustering. For the maximum data sets, all the values of above measures are getting optimal for proposed clustering algorithm.

• A. Data Sets

This paper uses 10 real data sets from kaggle site. These data sets include small to large data in size. Table 1 shows the details of data sets used.

Table 1. Data Sets Used

SN	Data Sets	Number of instances	Number of attributes
1	Accident	2057	15
2	Airline clusters	3999	7
3	Breast Cancer	569	30
4	Cities	493	10
5	Diamond	3089	11
6	Judges Rating	43	13
7	Rating1	2105	27
8	Salary	3123	6
9	Galaxy	3462	65
10	Voting	1076	5
11	Sensor1	8845	78

Table 2 shows results of standard k-means and proposed clustering algorithm with respect to efficiency.

Fig.2 to Fig.9 shows the performance of proposed, existing clustering algorithm and R-k-means clustering algorithms. Table 3 shows results of standard k-means and proposed clustering algorithm with respect to quality of clusters.

t able 2. t he efficiency of s tandard k-means v s . p roposed c lustering

Data sets	Algorithm	Accuracy	Running Time
Accident	Proposed Algo.	95.4	0.000581
	Standard k-means	93.81	0.000088
Airline Clusters	Proposed Algo.	98.7	0.00212
	Standard k-means	98.4	0.011
Breast cancer	Proposed Algo.	97.43	0.000551
	Standard k-means	96.65	0.000015
Cities	Proposed Algo.	99.31	0.000521
	Standard k-means	97.5	0.000061
Diamond	Proposed Algo.	98.25	0.000249
	Standard k-means	98.06	0.000669
Judges rating	Proposed Algo.	97.15	0.0011
	Standard k-means	90.94	0.00026
Rating 1	Proposed Algo.	79.37	0.000463
	Standard k-means	61.5	0.000039
Salary	Proposed Algo.	96.39	0.000666
	Standard k-means	95.8	0.000034
Galaxy	Proposed Algo.	99.86	0.00134
	Standard k-means	99.67	0.0122
Voting	Proposed Algo.	96.12	0.000559
	Standard k-means	95.44	0.000793
Sensor 1	Proposed Algo.	95.01	0.000891
	Standard k-means	85.67	0.0138

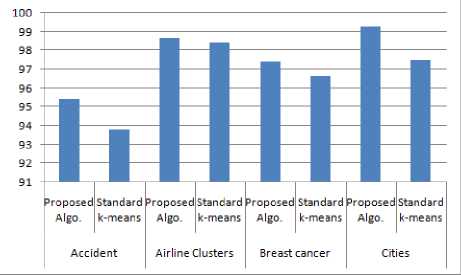
Fig.2. Accuracy of Proposed Algorithm

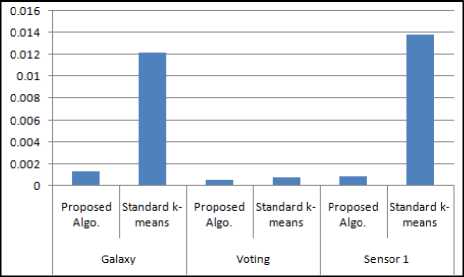
Fig.3. Running Time of Proposed Algorithm

Table 3. Clusters Quality of Proposed Clustering

Data sets	Algorithm	Silhouette Score	Dunn Score	CH Score	DB Score
Accident	Proposed Algo.	0.43	0.0025	3258.9	0.1
	Standard k-means	0.46	0.002	2434	0.77
Airline Clusters	Proposed Algo.	0.29	0.00078	0.0003	0.01
	Standard k-means	0.28	0.0003	2051.93	0.94
Breast cancer	Proposed Algo.	0.44	0.0079	1617.68	0.08
	Standard k-means	0.4	0.0071	1265.64	0.78
Cities	Proposed Algo.	0.35	0.0010	3224.34	0.07
	Standard k-means	0.34	0.0007	888.16	0.82
Diamond	Proposed Algo.	0.57	0.0060	19190.56	0.06
	Standard k-means	0.56	0.0026	19188.48	0.49
Judges rating	Proposed Algo.	0.69	0.33	96.17	0.13
	Standard k-means	0.23	0.27	34.04	0.88
Rating 1	Proposed Algo.	0.19	0.050	619.0	0.5
	Standard k-means	0.15	0.026	621.89	1.9
Salary	Proposed Algo.	0.36	0.0013	1071.01	0.02
	Standard k-means	0.35	0.0007	989.83	0.91
Galaxy	Proposed Algo.	0.53	0.01	91385.11	0.64
	Standard k-means	0.35	0.01	33459.76	0.88
Voting	Proposed Algo.	0.64	0.011	468.29	0.03
	Standard k-means	0.24	0.0038	388.16	1.0
Sensor 1	Proposed Algo.	0.55	0.0005	4194.5	1.11
	Standard k-means	0.5	0.0004	2063.7	0.88

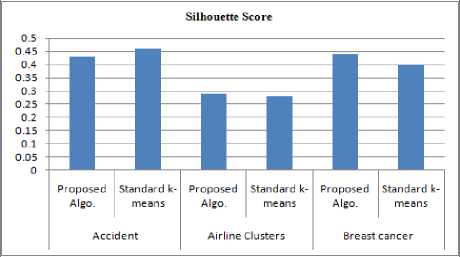
Fig.4. Silhouette Score of Proposed Algorithm

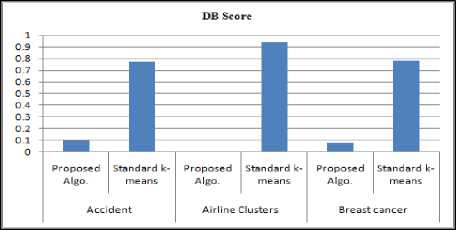
Fig.6. DB Score of Proposed Algorithm

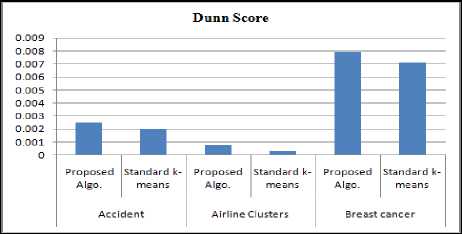
Fig.5. Dunn Score of Proposed Algorithm

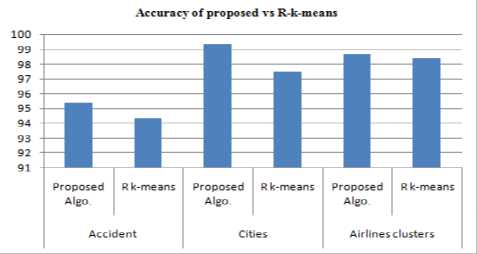
Fig.7. Accuracy of Proposed Algorithm

Table 4. Proposed Algorithm Vs. R-k-means

Data sets	Algo.	Accuracy	Run Time	Silhouette Score	Dunn Score	CH Score	DB Score
Accident	Proposed Algo.	95.4	0.000581	0.43	0.0025	3258.9	0.1
	R k-means	94.38	0.222	0.33	0.0033	2644	0.83
Cities	Proposed Algo.	99.31	0.000520	0.35	0.0010	3224.34	0.07
	R k-means	97.5	0.055	0.32	0.00079	908.29	0.92
Airlines	Proposed Algo.	98.7	0.00212	0.29	0.00078	2712	0.01
clusters	R k-means	98.4	0.89	0.27	0.00029	2147	1.04

Table 4 shows the R programming k-means and proposed clustering algorithm. R tool uses Lloyd’s algorithms in k-means [38-39].

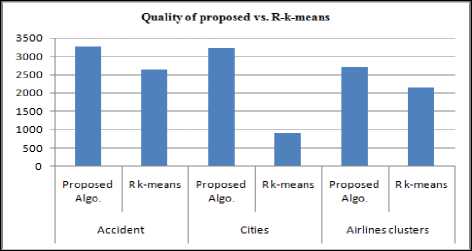
Fig.8. CH Score of Proposed Algorithm

Table5 shows the comparison of proposed clustering and other existing clustering algorithms.

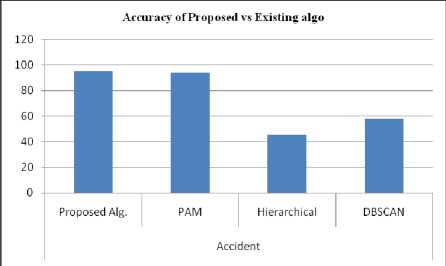
Fig.9. The accuracy of Proposed Vs. Existing Algorithms

Table 5. Existing Algorithms Vs. Proposed Algorithm

Data sets	Algorithms	Accuracy	Running Time	Silhouette Score	Dunn Score
Accident	Proposed Alg.	95.4	0.00058	0.43	0.0025
	PAM	93.97	10.18	0.43	0.001
	Hierarchical	45.43	0.0018	-0.027	0.0013
	DBSCAN	57.70	0.0076	-0.57	4236599
Cities	Proposed Alg.	99.31	0.00125	0.35	0.023
	PAM	97.11	0.0023	0.33	0.020
	Hierarchical	96.91	0.0032	0.30	0.021
	DBSCAN	80.01	0..0033	0.31	0.22
Airline Clusters	Proposed Alg.	96.22	2.27	0.33	0.00032
	PAM	96.22	2.27	0.33	0.00032
	Hierarchical	97.12	2.12	0.33	0.0032
	DBSCAN	95.12	1.23	0.30	0.0021

From the above results it is observed that as a number of instances in data sets increases, accuracy is also increased. Fig.10 shows this trend.

From the Table 3, it is observed that higher the number of instances of data sets then lower the value of silhouette score. This trend is shown in the Fig.11.

101			Accura су increases as Data Instances Increases
100 99 98 97
96
		2000    4000    6000

Fig.10. Accuracy increases as Data Instances Increases

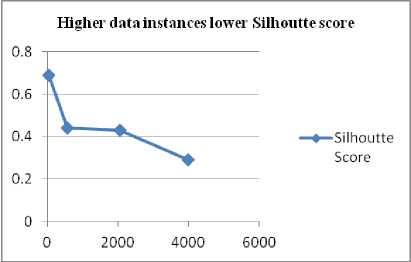
Fig.11. Higher Data Instances Lower Silhouette Score