Elaboration of atomic model for ab initio calculation of the ferrite / cementite interface

It is well known that solubility of carbon in the low-temperature bcc polymorphous modification of iron is very low, so that almost all carbon in commercial iron alloys (steels) usually containing 0,5 to 5 at. % C is present in the form of iron carbide Fe 3 C (cementite) co-existing with almost pure alpha iron (ferrite). In slowly cooled steels cementite is a part of a structural constituent called pearlite, a mixture of thin lamellae of ferrite and cementite [1]. Average interlamellar spacing of pearlite formed isother-mally from prior fcc gamma solid solution (austenite) depends on transformation temperature, ranging from 0,5…0,3 μ m when supercooling below the eutectoid temperature A 1 = 1000 K is Δ T = 30…50 K to ~0,1 μ m and even smaller if austenite is supercooled to about 830 K ( Δ T ≈ 170 K). Interlamellar spacing of pearlite significantly affects hardness and strength of steels [2].

Ferrite / cementite interfaces also play a role in trapping dissolved atoms of hydrogen. Hydrogen is one of important components in iron and steels. It has the smallest atomic radius among interstitial impurities (0,46 Å according to [3], which is confirmed by ab initio calculations [4]) and high diffusivity but low solubility in iron. From technical point of view hydrogen is a harmful impurity causing embrittlement, cracking etc. [5–7]. One of the ways of suppressing harmful effects of hydrogen is creating structural traps, i.e. positions where hydrogen atoms are bound and incapable of moving on the lattice [6–8]. One type of such traps are interphase interfaces, including α / Fe 3 C [6, 9].

Beside direct experimental studies, an important tool for quantitative analysis of hydrogen trapping is ab initio modelling. Previously the authors carried out such modelling of hydrogen interaction with substitutional impurity atoms [10] and vacancies [11, 12]. Ab initio modelling of hydrogen interaction with α / Fe 3 C interfaces requires determination of optimal modelling parameters and constructing a supercell describing the interface. This is the purpose of the present paper.

Atomic model

It is well known that cementite has an orthorhombic lattice of Pnma space group. Unit cell with room-temperature parameters a = 4,524; b = 5,088; c = 6,741 Å [13] contains 12 iron and 4 carbon atoms. Iron atoms occupy two crystallographically nonequivalent positions [14]: G (“general”):

Физика

± [[ x , y , z ]]; ± [[ 1/2– x , 1/2+ y , z ]]; ± [[ x , y , 1/2– z ]]; ± [[ 1/2– x , 1/2+ y , 1/2– z ]] (1 a ) and S (“special”):

± [[ u , v , 1/4 ]]; ± [[ 1/2– u , 1/2+ v , 1/4 ]]. (1 b ) Carbon atoms located in the centres of “normal” prismatic interstices [15] have coordinates

± [[ r , s , 1/4 ]]; ± [[ 1/2– r , 1/2+ s , 1/4 ]]. (1 c ) According to [16], parameters in eqs. (1) are x = 0,333; y = 0,175; z = 0,065; u = –0,167; v = 0,040; r = 0,43; s = –0,13.

There are two main types of orientation relationships (OR) between ferrite and cementite in pearlite, namely the Bagaryatskii (Isaichev) and Pitsch OR. For pearlite formed at small supercoolings fractions of colonies having each of the two OR’s are approximately equal, while with decreasing transformation temperature the probability of Bagaryatskii OR increases [17]. We will then concentrate our analysis on the Bagaryatskii type of OR. It supposes that the following planes are parallel in both phases:

(100) c ||(01¯1) α ; (010) c ||(11¯1¯) α ; (001) c ||(211) α , (2) and the habit plane of lamellae is (101) c || (112) α [17–19].

Fig. 1 shows cementite lattice projected on the (010) plane. Planes (101) in the iron sublattice of cementite form 12-layer stacking with average interplanar spacing of ₁ ¹ ₂■ V a ² + c ² = 0,677 Å (fig. 1). There are two types of these planes containing G and S atoms. It is most probable that the (101) c plane at the coherent ferrite / cementite interface will contain S type atoms because atomic pattern in S planes is more similar to that of (112) α planes [20].

For adequate description of macroscopic amounts of phases by ab initio modelling, periodic boundary conditions are to be set: the supercell in which electronic structure is calculated is supposed to be translated infinitely along all three axes. In order to provide integrity of the interface under these boundary conditions the interface has to be parallel to one of the faces of the supercell. In our case the coordinate system is to be changed in such a way that the habit plane (101) c || (112) α become parallel to one of coordinate planes. The supercell should consist of two parts, cementite and ferrite, each containing sufficient number of atomic planes to consider interaction of neighbouring interfaces insignificant.

Thus a reasonable way to construct the cementite part of the supercell is to change the three base vectors [ a , 0, 0], [0, b , 0], [0, 0, c ] to [– a , 0, c ], [0, b , 0], [ a , 0, c ], see fig. 2. The unit cell of cementite built up on new base vectors has the volume twice greater than the initial one and contains 32 atoms. The new cell is monoclinic; its parameters are a 1 = 8,118 Å; b 1 = 5,088 Å; c 1 = 8,118 Å; β 1 = 2 atan( a / c ) = 67,73°. It is also convenient to shift the origin of coordinates of the new cell along the initial x axis by (1/4 – 0,333) = –0,083 a in order to place the first S plane at z 1 =0 (see fig. 2).

The distance between the first and the last S planes in this cell (planes 0 and 13 in fig. 1) is 1,083 c 1 = 8,792 Å. The distance from the last cementite S plane located at z 1 = 1,083 to the first ferrite plane is to be chosen so that the average distance between iron atoms in these two planes be as close as possible to the interatomic distance in α iron a _α V32 = 2,482 Å, where a α = 2,866 Å is α iron lattice parameter. This condition is fulfilled if the distance between the two planes is 0,820 Å ( i.e. 0,109 c 1 ) and the initial atom in the first ferrite plane is located at x 1 = 0,368 и y 1 = 1/4 being shifted from the S atom [[0,167 a 1 ; 0,040 b 1 ; 1,083 c 1 ]] of the last cementite plane by [0,201 a 1 ; 0,210 b 1 ; 0,109 c 1 ]. Distances between iron atoms in the two planes are then 2,38...2,69 Å.

Interplanar distance for subsequent ferrite planes is to be a _α н 6 = 1,170 Å. Iron atoms in each next (112) α plane are shifted from the previous one by a vector 1 6 a _α [51¯2¯]; in new coordinates it corresponds to [ ¹ ₄ a ₁ - d cos β , ¹ ₃ b ₁ , ( d sin β ₁) c ₁] = [0,195 a 1 ; ¹ ₃ b ₁ ; 0,156 c 1 ].

Initial atom of the last ferrite plane is to be shifted from the initial S atom of the next (translated along z 1 ) supercell by [–0,201 a 1 ; –0,210 b 1 ; –0,109 c 1 ]. Since this S atom has coordinates x 1 = 0,250 and y 1 =0,540, then the number of ferrite planes in the supercell is to be taken such as to make the coordinates of the atom of the last plane close to x 1 = 0,049 and y 1 = 0,330. To provide this, seven ferrite planes are to be inserted, which yields the coordinates of the initial atom of the seventh plane x 1 = 0,040 and y 1 = 0,250. If the distance between neighbouring ferrite and cementite planes is again taken 0,886 Å, then the distances between iron atoms of the two planes are 2,43...2,65 Å.

With the added seven ferrite planes the O 1 z 1 size of the supercell increases from c 1 = 8,118 Å to c 2 = 18,150 Å, i.e. 2,236 times. The supercell now contains 64 atoms: 56 iron (28 in both ferrite and cementite parts) and 8 carbon (in the cementite part). It is shown in fig. 3.

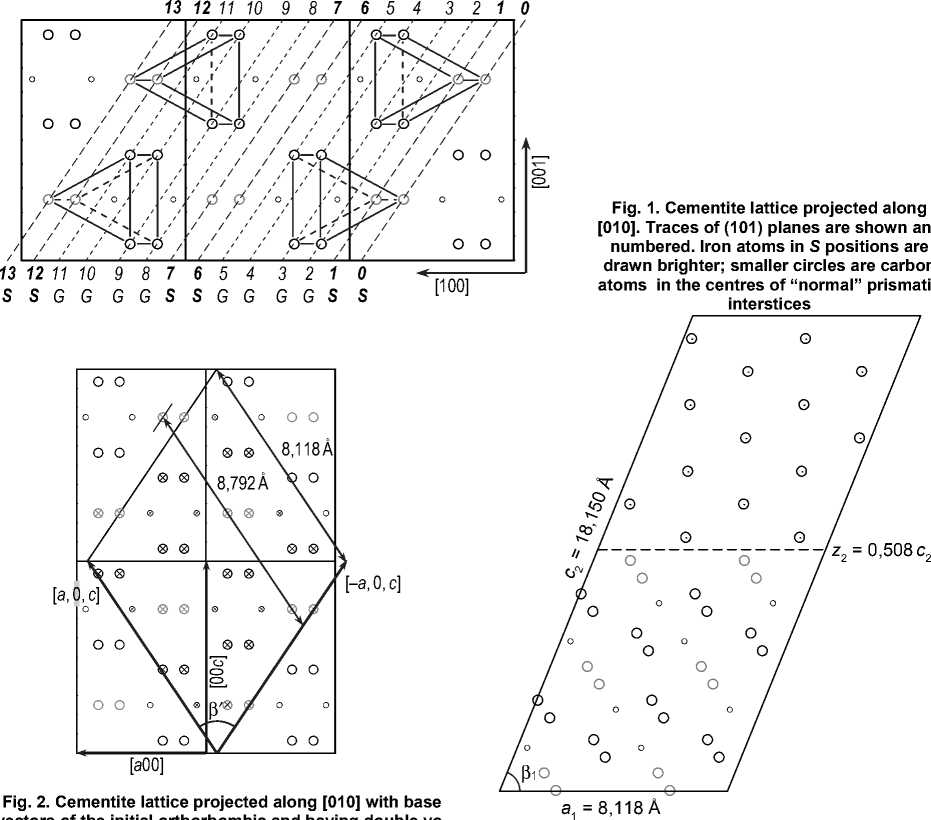
- lume monoclinic unit cells. Crosses indicate atoms included in the cementite part of the supercell

Fig. 3. Supercell containing both cementite and ferrite parts

Choice of ab initio modelling parameters

The above described supercell was used as initial structure for ab initio computer modelling. All calculations were performed by WIEN2k code [21] implementing linearized augmented plane wave (LAPW) method. Generalized gradient approximation (GGA) was chosen for calculations.

Supercells with monoclinic angles significantly different from 90° ( β 1 = 67,73°) are inconvenient for ab initio modelling in the WIEN2k. So the above described supercell was rebuilt by the program: translation periods changed to a 3 = 8,118; b 3 = 5,088; c 3 = 16,842 Å with β 3 = 94,221° and α 3 = γ 3 =90°.

Then optimal modelling parameters were defined. In the LAPW method the unit cell is divided into non-overlapping atomic spheres (muffin-tin spheres) having radius R mt , and the interstitial region. It is assumed that wave functions within muffin-tin spheres are combinations of spherical harmonics, and the charge density is thus spherically symmetric. Wave functions in the interstitial region are expanded into plane waves with the K max vector. Its value is one of the principal parameters that affect calculation accuracy because it determines the number of basis functions (matrix size). Another important parameter is the number of k -points. This value characterizes the discrete mesh used for numerical integration over the Brillouin zone. The higher it is, the more points are taken into account in the integration, the greater the accuracy, and the greater computer costs. The purpose of choosing optimal parameters is to provide high calculation accuracy (0,01 eV ≈ 1 mRy) at acceptable consumption of computer resources.

Физика

First optimization was performed for the number of k -points, since this parameter is independent of the others. Calculation parameters were the following: R _m ^Fe _t =2,0 a.u. [22]; R _m ^C _t = 1,4 a.u.; K max = 5,0 [22]; cut-off energy E cut = 7,0 Ry. As can be seen from fig. 4, when the number of k -points exceeds 64, the total energy E changes not greater than by 1 mRy, so 64 k -points may be accepted as the optimal value.

Optimal value of R mt for iron atoms is R _m ^Fe _t =2,0 a.u. [22]. Dependence of the system energy calculated using previously optimized parameters on R _m ^C _t is shown in fig. 5. As can be seen, at R _m ^C _t > 1,45 a.u. the total energy changes by less than 0,5 mRy, so the value R _m ^C _t = 1,45 a.u. was taken as optimal. Parameter R mt K max controlling convergence is then equal to 7,25.

Thus, the optimal parameters are following: number of k -points N k =64; parameter controlling the convergence R mt K max = 7,25; radii of atomic spheres R _m ^Fe _t =2,0 a.u. and R _m ^C _t = 1,45 a.u.

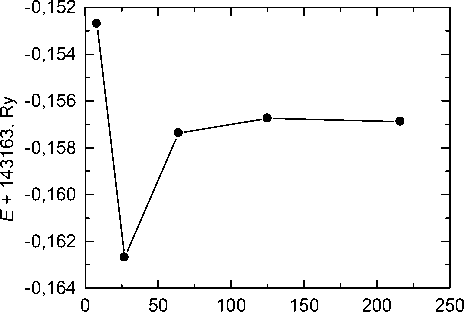
Number of k -points

Fig. 4. Dependence of the total energy of the system on the number of k -points

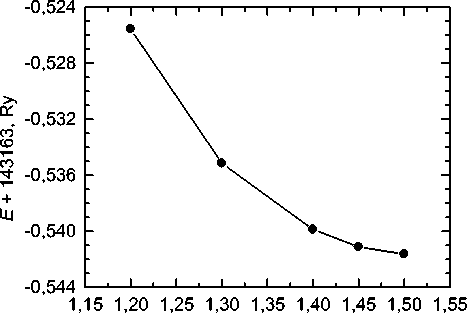
R _mt , a. u.

Fig. 5. Dependence of the total energy of the system on the muffin-tin sphere radius of carbon

Résumé

The supercell for ab initio modelling of the ferrite/cementite interface with Bagaryatskii orientation relationship and (101) c || (112) α habit plane has been built up and optimal values of parameters necessary for ab initio modelling have been determined. After additional volume optimization this supercell can be used for calculation of ferrite / cementite interfacial energy, interaction of the interface with impurities ( e.g. , hydrogen) and other lattice defects etc .