Electric vehicle charging scheduling and pricing based on Stackelberg game
Автор: Xiong Qiming, Zhang Zongnan, Bazhanov Andrei, Zhang Qi, Lu Jiahao
Журнал: Бюллетень науки и практики @bulletennauki
Рубрика: Технические науки
Статья в выпуске: 8 т.8, 2022 года.
Бесплатный доступ
The disorderly charging and discharging of a large number of electric vehicles will have a serious negative impact on the safety and economic operation of the power system. In order to avoid safety problems and obtain maximum economic benefits, a master-slave game is proposed to model the maximization of profits for agents and car owners. In the upper model of the model, the optimization objective of the main body is to minimize the operating cost and minimize the load mean square error; in the lower model, the goal is to minimize the cost of electric vehicles; the particle swarm algorithm is used, and the model decoupling characteristics are used from the inside to the outside. Solve the Nash equilibrium point of the optimization model, obtain the set of optimal time-of-use electricity price and electric vehicle charging and discharging scheme, and finally obtain the global optimal pricing strategy. Various typical scenarios before and after optimization are compared and analyzed in detail through calculation examples, and the effect of the proposed model and the overall scheduling benefit are verified.
Electric vehicle, electric vehicle network access, pricing, stackelberg game, two-tier optimization
Короткий адрес: https://sciup.org/14125303
IDR: 14125303 | УДК: 629.064.5 | DOI: 10.33619/2414-2948/81/39
Текст научной статьи Electric vehicle charging scheduling and pricing based on Stackelberg game
Бюллетень науки и практики / Bulletin of Science and Practice Т. 8. №8. 2022
UDC 629.064.5
With the increasing pressure on global resources and the environment, people have begun to actively look for alternatives to traditional fuel vehicles that use fossil fuels as the main energy source. Electric vehicles have attracted more and more attention due to their great advantages in energy saving and emission reduction. According to the research report on the electric vehicle development strategy of the Ministry of Industry and Information Technology, the number of electric vehicles in the country will reach 60 million in 2030 [1]. Such a large-scale electric vehicle, no matter what charging method is used, has a considerable impact on the economic benefits of the power grid [2-4]. Since the number of electric vehicles may be quite large, it is unrealistic for the dispatching agency to uniformly manage each electric vehicle. A more feasible solution is to establish agents in residential areas to implement decentralized management of electric vehicles. Therefore, the optimization of agent interests is another important issue. Demand-side management is a way of motivating users to adopt specific consumption patterns through price signals. It has been widely used in electricity price setting and load regulation management in power systems. Generally, by formulating a certain electricity price range, users are encouraged to respond, so as to optimize the load curve and reduce the peak-to-valley load deviation of the distribution network. a large economic benefit [5]. Therefore, the research on the impact of large-scale electric vehicles on the economic benefits of the power grid and the charging control strategy with the goal of minimizing user costs have increasingly become a hot issue of concern. At the same time, as a key part of the electric vehicle market, the income of charging station operators and the charging fees of users play an important role in the promotion and application of electric vehicles [6, 7]. Reference [8] considers user satisfaction and other factors, establishes a demand response model for electric vehicles based on time-of-use electricity prices, and uses an optimization algorithm to solve the optimal time-of-use electricity price scheme, and uses electricity price means to guide the charging and discharging behavior of electric vehicles. Reference [9] proposes an optimization model and method for the peak and valley electricity price period, and solves the optimization problem of the peak and valley electricity price period. Reference [10] takes the slow charging mode of private electric vehicles as the research object, and proposes a dualsequence valley period maximizing orderly charging control method, which maximizes the use of valley period for charging, and does not expand the capacity of the power distribution equipment in the community. It can meet as much as possible the charging needs of residential electric vehicles for users in the community. Reference [11] proposes a charging optimization strategy based on real-time electricity prices. Electric taxis can reduce charging costs and maximize operating benefits by selecting the optimal charging time period. The above article provides guidance for the research on the orderly charging guidance strategy of electric vehicles.
This paper studies the optimization of the interests of agents and electric vehicle owners. First, agents do not need to directly intervene in the charging and discharging behavior of electric vehicles, but only need to set the charging service price at each time period as a key factor to guide the orderly
Бюллетень науки и практики / Bulletin of Science and Practice Т. 8. №8. 2022 charging of electric vehicles. Second, users are no longer completely "takers" of the price, they can choose the charging time independently. More importantly, the competitive relationship between agents and users is through the stackelberg game, and the interests of all parties can be maximized at the equilibrium of the game.
In order to realize the optimal scheduling of the charging and discharging behavior of electric vehicles, it is not only necessary to formulate a reasonable electricity price incentive mechanism, but also the support of smart grid-related technologies. For the identification of electric vehicles, the transmission of recently declared information, and the issuance and execution of agent scheduling orders, it can be achieved through the effective combination of wired communication (such as optical fiber) and long-distance wireless communication. These technologies are quite mature in the field of communication and can support the realization of optimal scheduling problems for electric vehicles [12]. The steps of scheduling plan formulation are as follows.
Step 1: The owner of the vehicle should report to the agent the day before based on the usage of the electric vehicle the next day.
Step 2: Each agent first summarizes the declaration information of the car owner, and then divides the electric vehicles into sets based on the similar merged data grouping technology. And report the dispatchable capacity of each period to the system dispatching agency.
Step 3: The system scheduling agency formulates the scheduling of each agent in each time period with a given scheduling objective (such as peak shaving and valley filling, smoothing the intermittency of renewable energy power generation, etc.) according to the reporting status of each agent. plan (including charging load and discharge output), and send relevant scheduling information to each agent.
Step 4: Each agent optimizes the charging and discharging time of each electric vehicle set according to the reporting situation of the vehicle owner, and optimizes the charging and discharging time of each electric vehicle set with the goal of minimizing the deviation between the actual dispatching result of the agent and the dispatching plan determined by the system dispatching agency. The load/output deviation is sent to the system dispatcher.
Step 5: The system scheduling agency comprehensively considers the scheduling objectives and scheduling deviations of the agents, adjusts the scheduling strategy with a given rule, and sends the results to each agent; repeat steps 4 and 5 until the given rules are reached. set convergence conditions.
The revenue of the agent depends on the charging strategy of the electric vehicle, and the charging of the electric vehicle is not directly controlled by the agent, but depends on the electricity price set by the agent. Under the above framework, the key problem that the agent needs to solve is to formulate the electricity price for each time period of the next day. Different from the traditional optimization problem, according to the price agreement, the average daily electricity price is fixed. If the agent raises the electricity price in a certain period, the electricity price in other periods is bound to be lower than the average value. The smart terminal will automatically select the time period when the electricity price is low to charge. It can be seen that the relationship between the agent and the user naturally constitutes a master-slave game. Furthermore, in the market structure studied in this paper, grid companies are responsible for organizing energy transactions in the electricity market, and do not directly participate in or profit from energy management in the retail market. The interests of the power grid company are reflected in the following: the charging behavior of a large number of electric vehicles presents a deterministic load demand to the grid through the power purchase contract of the agent, which reduces the difficulty caused by random charging and discharging behavior to the grid dispatching.
Бюллетень науки и практики / Bulletin of Science and Practice Т. 8. №8. 2022
Non-cooperative game models include the Cournot model based on output competition and the Bertrand model based on price competition. The Cournot model is mainly to solve the problem that the participants in the duopoly market take the behavior of output competition at the same time; the Bertrand model is mainly to take the behavior of the participants to take the price competition at the same time. Actors in both models perform decision-making actions simultaneously. The stackelberg model belongs to a dynamic non-cooperative game, and the players participating in the game do not have the same market position, so there are time-series points in the decision-making behavior. The first movers refer to their own factors to make decision-making behaviors, and the latter movers obtain the decision information of the first movers, and then combine their own factors to make plan decisions. Stackelberg can solve the following problems:
-
(1) The actors participating in the game are independent and have their own relevant decisionmaking basis.
-
(2) Participation in decision-making affects at least the benefits obtained by one other participant;
-
(3) In the process of participating in the game, the decision-making behavior of the participants has obvious timing, and there is a difference between the two. As for the master-slave relationship.
-
(4) The final decision made by the participants should ensure that each participant is within an acceptable range. The core of the game problem solution is equilibrium. When the game reaches the Nash equilibrium, any participation cannot obtain higher returns by modifying its own strategy on the premise that other participants do not change their own decisions. The definition expression is that S * = ( S _,-- SS*,---S*n ) is the decision vector of all participants, if the condition u i ( $ , S * i ) > ui ( Si , S\ ) , V s ;<= S holds, then s * is a Nash equilibrium. where Si denotes the policy set of all actors i, and S * and S_t denote the policy of player i and the policies of all players except i, respectively. The above formula shows that when the game finally reaches the Nash equilibrium, no matter how a player adjusts his strategy, he cannot obtain higher benefits.
In the pricing master-slave game, the upper decision maker is the agent, and the lower decision maker is the electric vehicle owner. The game structure is shown in Figure 1.
A two-tier optimization model for agency pricing

upper model
Max Agent's profit S.t.

® Energy storage equipment constraints )
¥
charging strategy

Charging price
Min Electric vehicle owner charging costs S.t.
lower model
Figure 1. Schematic diagram of the master-slave game structure
The optimization problem of the agent is as follows, the decision variable is { ct , E t , E , E-, r , rt- , Z t , U t , V t } :
max EZ ctPit+E(n- Et-П Et- nt E+)(1)
tit s.t. c1 < ct < ctu, Vt(2)
T
Z c t / T = c av t = 1
Et > 0,0< E+ 0 < e;< rt -(1 - zt), V t(5) У pit + r+ - r- = Et + E+ - E—, Vt it t t t tt 0< rt+< uRm ,0 < r_<(1- Ut) Rm,Vt '0 < St = St-1 + n+rt+-rf / n -< smax, V t I s1 = St = S 0 where: ct is the charging price in period t; E is the contracted electricity in the day-ahead market t period; E+, Et is the purchase and sale of electricity from the real-time market in the t period; rt+ , rt is the charging and discharging capacity of the energy storage device in the t period; zt is a Boolean variable, representing the energy transaction status in the t period; ut is a boolean variable, indicating the state of the energy storage device in the t period; pit is the charging power of the ith electric vehicle in period t; nt+, nt is the real-time market purchase and sale electricity price in t period; rf is the market contract electricity price before time period t; ct , cu is the lowest and highest electricity price in period t; cav is the average daily electricity price; Rm, Rm is the maximum charging and discharging power of the energy storage device; П+, П is the charging and discharging efficiency of the energy storage device; Smaxis the maximum capacity of the energy storage device; S0is the initial capacity of the energy storage equipment; T is the total number of periods; M is a large enough normal number, which can be taken as the maximum transaction power in the real-time market. In the above formula, the objective function formula (1) maximizes the profit of the agent. The profit of the agent consists of 4 parts, of which the first item represents the income from selling
Бюллетень науки и практики / Bulletin of Science and Practice
Т. 8. №8. 2022
electricity to users; the second item is the income from selling electricity to the real-time market; the third item is the cost of purchasing electricity in the day-ahead market; the fourth item is the real-time market The cost of purchasing electricity. It is assumed that the electricity price in the day-ahead market is lower than the electricity price in the real-time market, that is nt< nt .Constraint (2) is the upper and lower bounds of pricing, and Equation (3) is the average price constraint. Constraints (4)-(6) together constitute the power balance condition. Among them, the integer variable zt in equations (4) and (5) restricts that at most one of Et and Et can be strictly greater than 0. Since the retailer's electricity sales to the real-time market is limited by the capacity of the energy storage equipment, there is Et< rt considering the complementary relationship between E} and Et , and there are constraints (4) (5). In fact, due to the influence of the energy storage device and the maximum charging power of electric vehicles, E} must be less than the sum of the maximum charging power of all electrical equipment. Therefore, the parameter M in equation (4) can also be taken as the sum of the maximum charging power of all electrical equipment. It should be pointed out that under normal circumstances, since the real-time market electricity price is higher than the day-ahead market electricity price in the same period, the agent will not directly purchase electricity from the real-time market in the optimal charging strategy. However, there are various uncertainties in reality, such as the temporary departure of some electric vehicles or the need for temporary charging services. When the charging strategy is implemented in a rolling optimization manner, the user information will be updated every time period, and the purchase and sale of electricity in the real-time market is retail. Providers provide a means of coping with a variety of uncertainties. Constraint (7) limits the rate of charge and discharge of the energy storage device, and the integer variable ut restricts that at most one of rt+ and rt is strictly greater than 0, that is, the energy storage device cannot be in the state of charging and discharging at the same time. Constraint (8) is the state of charge equation of the energy storage device, and the state of charge of the energy storage device in the last period is equal to the initial state of charge, making the state of charge (SOC) of the energy storage device periodic. { pit} is the charging power of electric vehicle i in period t, which corresponds to the optimal charging strategy of electric vehicle. The optimization problem of the lower-level decision maker electric vehicle i in the game is as follows: { Pit } = argmin 2 ctPit t s.t. V p = 0.9Em - E° itii t eT where: Eim is the battery capacity of the i-th electric vehicle; Ei0is the initial charge of the i-th electric vehicle battery; pim is the maximum charging power of the i-th electric vehicle; Ta is the charging period for the electric vehicle. In the above formula, the objective function formula (9) represents the minimization of the selfcharging cost under the electricity price given by the agent. Constraint (10) indicates that the charging amount of the electric vehicle should make the battery reach the corresponding charge level. Constraint (11) is a limit on the charging speed. Constraint (12) indicates that the charging power is 0 during the unavailable charging period. The agent problems (1-8) and all electric vehicle problems (9-12) constitute a Stackelberg game. The game was originally proposed by Stackelberg in literature [12], literature [13] studied the solution method when the game is linear, and literature [14] extended this method to the case where the game is convex. Different from the model proposed in the literature [15], since the electricity price is given when the electric vehicle decision is made, the electric vehicle problem is a linear programming; and in the problem equations (1)-(8), since the agent needs to consider the price of the electric vehicle. reaction, Therefore, both q and q are variables, so the game problem posed by agents and electric vehicles is neither linear Sex is not convex either. The following will simulate the game interaction process of electricity prices between agents and users based on particle swarm algorithm. Using the CPLEX solver in the YALMIP toolbox can effectively solve the complex problems between large-scale agents and car owners and can effectively solve the PSO heuristic search. The shortcomings of the randomness of the algorithm, so as to find the equilibrium point of the game. Because the particle swarm algorithm has a fast convergence speed and a certain memory, it can well simulate the game interaction process of electricity prices between agents and users. At the same time, the collaborative optimization of individuals and groups helps to quickly find the equilibrium solution of the game; the established model It has a large number of equation constraints and fully considers the characteristics of the randomness of electric vehicles and the heterogeneity of air conditioning at the user level. It is a large-scale complex optimization problem. The CPLEX solver in the YALMIP toolbox can effectively solve large-scale complex problems. It can effectively solve the shortcomings of the randomness of the PSO heuristic search algorithm and the game model solution process is as follows: 1) Set the number of particle swarms and the number of iterations; 2) Initialize the parameters of particle swarm algorithm to generate initial particles of electricity price information; 3) The lower-level users use CPLEX to solve the optimal electricity consumption behavior curve according to the electricity price; 4) The upper-layer microgrid operator reasonably regulates the energy storage system according to the upper-layer user's electricity consumption behavior curve to realize its own maximum profit; 5) The maximum income of the above-layer micro-grid operator is taken as the target value of the particle fitness function. Based on the set parameters, the the velocity and position of the new particle; In this section, the validity of the model and solution method proposed above is illustrated by an example. At the same time, the influence of factors such as the proportion of different types of electric vehicles, the capacity Smaxof energy storage equipment and the lower limit of pricing Cminon the profitability of agents and the charging cost of electric vehicle owners is analyzed. In order to facilitate the display of the calculation results, this example assumes that the electric vehicles can be divided into 3 groups after equivalent aggregation, and each group has N=[50, 20, 10] electric vehicles. The rechargeable time of each group of electric vehicles is shown in Table 1 Table 1 (Y means rechargeable, N means non-rechargeable). Group 1 represents the "early departure type"; Group 2 represents the "normal schedule type"; Group 3 represents the "night shift type". The electric vehicle parameters after equivalent aggregation are shown in Table 2. Here, the "early departure and late return type" is predominant. The market price of electricity a day ago is shown in Table 3. The electricity purchase price in the real-time market is generally higher than the electricity purchase price in the day-ahead market. In this example, it is assumed that nt+ = nt = 1.2n, . The upper limit c“ = nt+ of retail electricity price, the lower limit c} = 0.8nd, the average value cav = 0.5 Y/(kw.h) , the parameters of energy storage equipment are shown in Table 4. Table 1 ELECTRIC VEHICLE CHARGING PERIOD Time Group 1 Group 2 Group 3 1 Y Y N 2 Y Y N 3 Y Y N 4 Y Y N 5 Y Y N 6 Y Y N 7 N Y N 8 N Y N 9 N N Y 10 N N Y 11 N N Y 12 N N Y 13 N N Y 14 N N Y 15 N N Y 16 N N Y 17 N N Y 18 N N Y 19 N N Y 20 N Y Y 21 N Y N 22 Y Y N 23 Y Y N 24 Y Y N
Бюллетень науки и практики / Bulletin of Science and Practice
Т. 8. №8. 2022
Table 2 ELECTRIC VEHICLE PARAMETERS parameter Group 1 Group 2 Group 3 Em/(kW⋅h) 36 36 36 E0/(kW⋅h) 12 12 12 Pm/kW 6 6 6 Table 3 DAY-AHEAD MARKET ELECTRICITY PRICES period price/¥ period price/¥ period price/¥ 1 0.35 9 0.52 17 0.81 2 0.33 10 0.58 18 0.75 3 0.30 11 0.66 19 0.64 4 0.33 12 0.75 20 0.55 5 0.36 13 0.81 21 0.53 6 0.40 14 0.76 22 0.47 7 0.44 15 0.80 23 0.40 8 0.46 16 0.83 24 0.37 PARAMETERS OF ENERGY STORAGE EQUIPMENT Table 4 Rm+ Rm- s max S0 η+ η- 1500 1500 8000 3000 0.9 0.9 Using the data in Section 4.1 and using CPLEX to solve the problem, the maximum profit of the agent is 3554.45 ¥, and the optimal strategy of the agent is shown in Table 5. The charging strategy of electric vehicles is shown in Table 5 Table . Since the number and capacity of group 1 EVs are significantly more than those of the other 2 groups, it can be seen from Table 5 that the agents always set the electricity price to the upper/lower limit during the available/unavailable charging period of group 1 EVs to meet the average price . Since the real-time market power purchase price is higher than the day-ahead market, it is theoretically unnecessary to purchase power from the real-time market. This setting is to deal with uncertain factors such as the temporary departure of electric vehicles during application. On the other hand, the strategy corresponding to Table 6 minimizes the charging cost per EV, so rational car owners have no tendency to deviate from this strategy. Therefore, at the electricity price shown in Table 6, the charging of electric vehicles becomes an orderly behavior. Table 5 RETAIL’S OPTIMAL PRICING STRATEGY T price Day Purchased Real purchase Real sales power storage 1 0.396 1168 0 0 3900 2 0.396 1420 0 0 4800 3 0.36 1420 0 0 5700 4 0.396 1420 0 0 6600
Бюллетень науки и практики / Bulletin of Science and Practice
Т. 8. №8. 2022
T price Day Purchased Real purchase Real sales power storage 5 0.396 1000 0 0 7500 6 0.396 555.5 0 0 8000 7 0.396 0 0 0 8000 8 0.541 60 0 0 8000 9 0.541 60 0 0 8000 10 0.541 24 0 0 8000 11 0.541 0 0 200 7777.7 12 0.6 0 0 1000 6666.6 13 0.648 0 0 1000 5555.5 14 0.608 0 0 1000 4444.4 15 0.64 0 0 1000 3333.3 16 0.664 0 0 1000 2222.2 17 0.648 0 0 1000 1111.1 18 0.6 0 0 1000 0 19 0.541 0 0 0 0 20 0.541 60 0 0 0 21 0.424 333.3 0 0 300 22 0.396 1000 0 0 1200 23 0.396 1000 0 0 2100 24 0.396 1000 0 0 3000 EVS’ OPTIMAL CHARGING STRATEGIES Table 6 Time Group 1 Group 2 Group 3 1 120 48 0 2 300 120 0 3 300 120 0 4 300 120 0 5 0 0 0 6 0 0 0 7 0 0 0 8 0 0 60 9 0 0 60 10 0 0 24 11 0 0 0 12 0 0 0 13 0 0 0 14 0 0 0 15 0 0 0 16 0 0 0 17 0 0 0 18 0 0 0 19 0 0 0 20 0 0 60 21 0 0 0 22 0 0 0
Бюллетень науки и практики / Bulletin of Science and Practice
Т. 8. №8. 2022
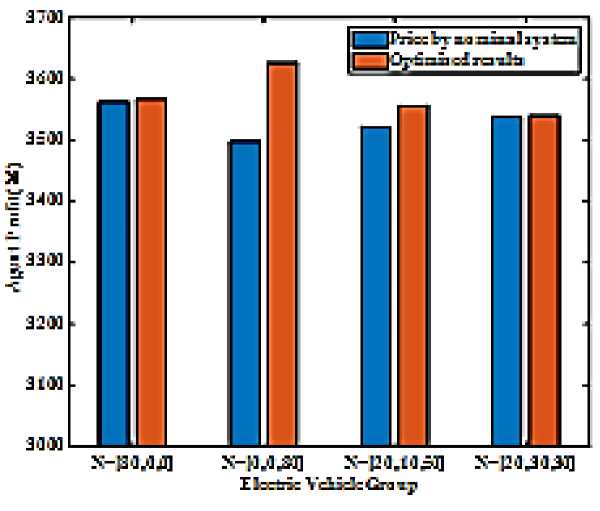
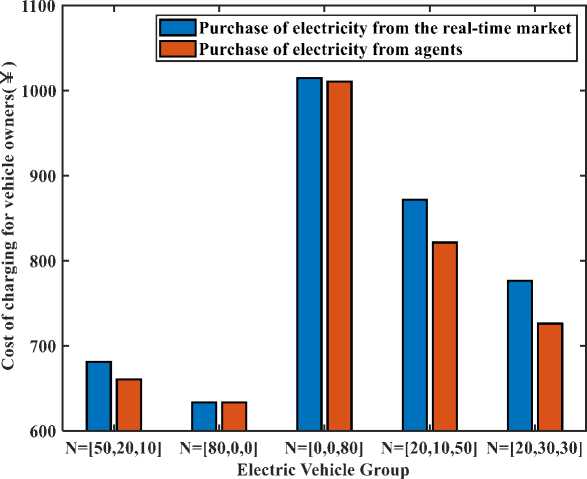
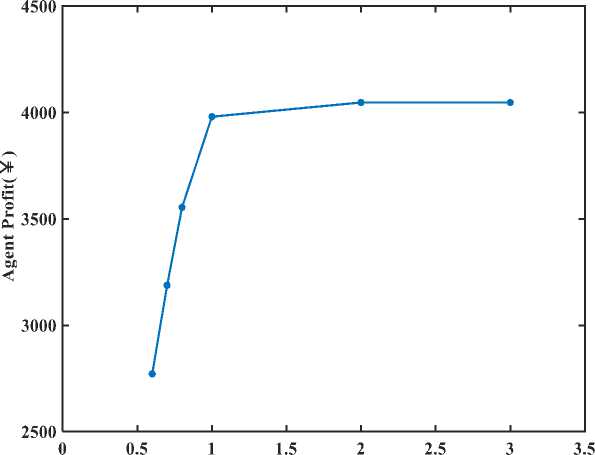
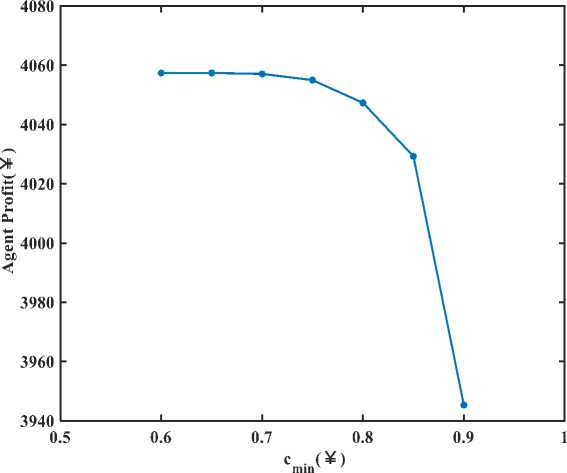
Time Group 1 Group 2 Group 3 23 0 0 0 24 0 0 0 On the premise of ensuring that the total number of electric vehicles in the three groups is constant, change the proportion of electric vehicles in each group, taking N=[20, 10, 50] vehicles and N=[20 30, 30] vehicles. The results obtained are shown in Figure 2. It can be seen that under different proportions of electric vehicles, the optimal price is not the same, which is mainly affected by the proportion of electric vehicles of each charging type. When the "going out early and returning late" type is dominant, due to the large demand for charging at night, the nighttime pricing will be relatively high; when the "night shift type" is dominant, the situation is reversed. Still using the charging electricity price in Table 6, unchanged, considering the proportion of different types of electric vehicles, the obtained a ent rofit and otimization results are shown in Fi ure 3 Figure 2. Real-time price sequence and upper/lower bounds under different N Figure 3. Comparison of retail’s profit under different N and corresponding real-time price It can be seen that, using the method in this paper, the profit of the agent is greater. At the same time, the following information can be obtained: 1) When the types of electric vehicles are concentrated (such as N=[80,0,0], N=[0,0,80]), the profit of the agent is the highest. Evenly, the profit of the agent gradually decreases. This is because when a single type dominates, the agent can obtain the maximum profit by setting the chargeable/non-chargeable period price of the type to the highest/lowest and satisfying the average value; when the proportion of the three types is close, due to the limitation of the average value, the agent will The charging price of each time period of the merchant cannot be set too high, which will reduce its total profit. 2) When the "night shift type" is dominant, the profit of the agent is greater than that when the "early departure type" or "normal work and rest type" is dominant. This is because the charging time of the "night shift type" is during the day, and the real-time market electricity price during the day is higher than that at night, so the pricing cap is also higher than at night, so the agent can set the price higher to get more profit . It can be seen from Figure 4 Ошибка! Источник ссылки не найден.that the cost of purchasing electricity from the dealer is lower than the cost of purchasing electricity directly from the real-time market, which is beneficial to the implementation of the dealer management method. At the same time, when the "night shift type" dominates, the charging cost of car owners increases significantly. This is because the charging time of the "night shift type" is during the day, and the agent can set the charging price higher to obtain greater profits, which also increases the charging cost of electric vehicle owners. However, car owners still benefit from this point of view, as the cost of charging is still lower than the cost of buying electricity directly from the real-time market. The above results show that the electricity price of agents determined according to the method proposed in this paper is related to the needs of users. This pricing method has better flexibility than using a constant electricity price. Influence of energy storage equipment capacity on optimal solution Let S vary from 6000 kw.h to 30000 kw.h ,The change of agent profit is shown in Figure 5. Figure 4. Comparison of consumers’ cost under different N and corresponding real-time price S (104kWh) max Figure 5. Comparison of retail’s profit under different S It can be seen from Figure 5 that with the increase of the maximum capacity Smax of the energy storage equipment, the profit of the agent first increases and then remains unchanged. When Smax increases to a certain level, more capacity cannot be used due to the limitation of the charging and discharging rate of the energy storage device, so the profit of the agent reaches saturation. Change the lower limit of pricing, from 0.6 times the day-ahead market contract electricity price to 0.9 times the day-ahead market electricity price, the profit of the agents and the changes in the charging cost of electric vehicle owners are shown in Figure 6 and Figure 7. Figure 6. Comparison of retail’s profit under different floor price It can be seen from Figure 5 and Figure 6 that with the increase of the lower limit of pricing, the pricing of the non-charging period or the charging period of less electric vehicles will increase. Due to the limitation of the average price, the pricing of charging periods of many electric vehicles will decrease, and the profit of the agent will decrease, the owner's charging cost has dropped. Therefore, in order to protect the interests of agents and not harm the interests of car owners, the lower limit of pricing cannot be too high or too low, and an appropriate value should be selected comprehensively. After a large number of electric vehicles are widely used, if they are allowed to charge in disorder, it will threaten the safety and economic operation of the power system. On the other hand, the energy storage characteristics of electric vehicle batteries help to improve the safety and economy of system operation. In this way, how to optimally schedule and control the charging and discharging process of electric vehicles to maximize economic benefits and minimize negative impacts has become an important issue worthy of study. In this context, this paper constructs a Stackelberg game scheduling architecture model for electric vehicles and agents. Considering the response of electric vehicle charging strategy to price, it can reduce user costs and achieve a win-win situation for agents and car owners. The particle swarm algorithm has a fast convergence speed and a certain memory. It can well simulate the game interaction process of electricity prices between agents and users. At the same time, the collaborative optimization of individuals and groups helps to quickly find the equilibrium solution of the game and can find the most optimal solution. optimal pricing strategy. A numerical example verifies the effectiveness of the method proposed in this paper. The calculation results show that the electric vehicle charging electricity price should change with the demand to improve the profit of the agent. Increasing the capacity of energy storage equipment within a certain range is another effective way for agents to increase revenue.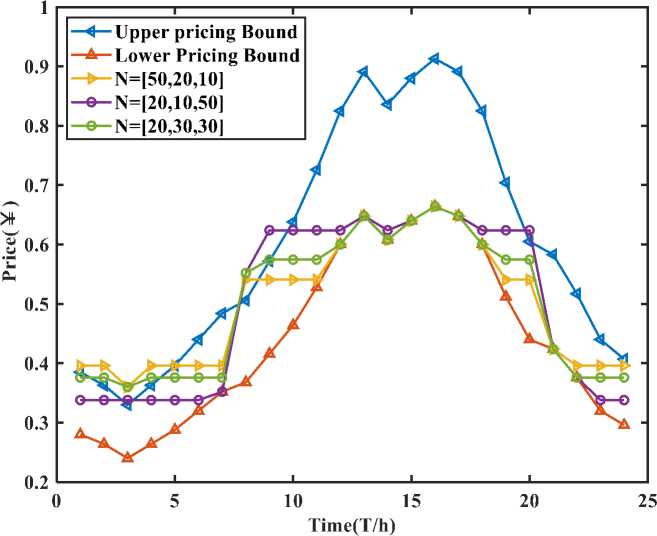
Список литературы Electric vehicle charging scheduling and pricing based on Stackelberg game
- Zhang, W., Wu, B., Li, W., & Lai, X. (2009). Discussion on development trend of battery electric vehicles in China and its energy supply mode. Power System Technology, 33(4), 1-5.
- Li, Z., Guo, Q., Sun, H., & Xin, S. (2014). Real-time charging optimization method considering vehicle charging prediction. Automation of Electric Power Systems, 38(9), 61-68.
- Zhang, M., Tian, L., & Yang, S. (2014). Influence of electric vehicle charging load distribution on power grid. Power Syst. Protect. Control, 42(21), 86-92.
- Wang, J., Wu, K., Liu, Z., Wu, K., & Sun, W. (2013). Impact of electric vehicle charging on distribution network load and coordinated control. Electric Power Automation Equipment, 33(8), 4752.
- Xiang-ting, C., Yu-hui, Z., Wei, D., Jie-bin, T., & Yu-xiao, G. (2010, September). Design of intelligent Demand Side Management system respond to varieties of factors. In CICED 2010 Proceedings (pp. 1-5). IEEE.
- Fengquan, Z., Zhanwei, L., Xiaolei, W., Xiaohui, Y., & Yishan, X. (2010). Discussion on operation mode to the electric vehicle charging station. Power System Protection and Control, 35(21), 63-66.
- Wang, D., Guan, X., Wu, J., & Gao, J. Y. (2014). Vehicle driving pattern based modeling and analysis of centralized charging/discharging strategy for plug-in electric vehicles. Power System Technology, 38(9), 2322-2327.
- Lu, Mengkuo (2014). Research on time-of-use electricity price suitable for charging and discharging of electric vehicles. Beijing: North China Electric Power University.
- Ge, S., Wang, L., Liu, H., Feng, L., Huang, M., & Zhu, T. (2013). An optimization model of peak-valley price time-interval considering vehicle-to-grid. Power System Technology, 37(8), 23162321.
- Su, H., & Liang, Z. (2015). Orderly charging control based on peak-valley electricity tariffs for household electric vehicles of residential quarter. Electric Power Automation Equipment, 35(6), 17-22.
- Yang, Z., Sun, L., Chen, J., Yang, Q., Chen, X., & Xing, K. (2014). Profit maximization for plug-in electric taxi with uncertain future electricity prices. IEEE Transactions on Power Systems, 29(6), 3058-3068. https://doi.org/10.1109/TPWRS.2014.2311120
- Yao, W., Zhao, J., Wen, F., Xue, Y., & Xin, J. (2012). A charging and discharging dispatching strategy for electric vehicles based on bi-level optimization. Automation of Electric Power Systems, 36(11), 30-37.
- Von Stackelberg, H. (1934). Marktform undgleichgewicht. J. springer.
- Anandalingam, G., & White, D. J. (1990). A solution method for the linear static Stackelberg problem using penalty functions. IEEE Transactions on automatic control, 35(10), 1170-1173. https://doi.org/10.1109/9.58565
- Shimizu, K., & Lu, M. (1995). A global optimization method for the Stackelberg problem with convex functions via problem transformation and concave programming. IEEE Transactions on Systems, Man, and Cybernetics, 25(12), 1635-1640. https://doi.org/10.1109/21.478451


