Electron scattering on a wormhole in the Born approximation

Since John Wheeler introduced the concept “wormhole” in 1957, wormholes have caused a huge interest among relativistic researchers, and till now this interest does not decrease. In particular, it is worth noting the message [1], which states that as of January 19, 2023 the word “wormhole” for all time occurs in the titles of 1614 articles on the resource ArXiv.org, and for the last 12 months 175 articles have this term in their titles. Over the past decades, scientists have done a lot of work to study the nature of wormholes, but there are still many unsolved problems. Nevertheless, scientists remain optimistic and, moreover, researchers are making various efforts to search for astrophysical wormholes

• ¹    E-mail: WTimoff@yandex.ru

in the Universe [2]. The main method of wormhole detection is currently gravitational lensing [3,4]. After the Event Horizon Telescope project obtained an image of the shadow of a black hole in the center of the galaxy M87 [5], the method of wormhole detection by its shadow became relevant [6-8]. Researchers are most interested in traversable wormholes. Such wormholes would allow to travel long distances without violating the velocity limit. In GR, for wormholes to be traversable, the presence of exotic matter is required [9-14]. Traversable wormholes that are not filled with an exotic type of matter are possible only in alternative theories of gravity [15-25]. However, unfortunately, one cannot be sure in the absolute correctness of any theory of gravitation for our Universe. Therefore, it is impossible to state definitively that the existence of traversable wormholes requires the presence or absence of exotic matter. Nevertheless, it is concluded in this work within the framework of GR that by means of a particle stream directed to the wormhole it is possible to create such a condition under which the wormhole could remain open without exotic matter. Thus, the following task is set: to find out within the framework of the Born approximation, what are the properties of the flux of electrons which are scattered on the Ellis-Bronnikov wormhole.

To solve the task, let us:

• 1.    determine the Green’s function for the Dirac equation in the gravitational field;

• 2.    convert the Dirac equation to the integral form;

• 3.    find the scattering amplitude in the Born approximation;

• 4.    calculate the total cross sections for elastic and inelastic scattering;

• 5.    describe the properties inherent in the character of electron scattering on a wormhole.

• A.    Green’s function

It is known that the Green’s function G _o （ £ — х^ of the Dirac equation for a free particle

〃丁 （ a ） d a j — m^ = 0

satisfies the equation

〃T（a）daGo （审—£ ） — mGo （审—£）= 6（£ — £） and has the form

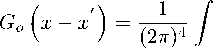
/ + m

评 — m ²

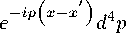
（1）

where p = т （ а ） Р а ・

Similarly, we can define the Green’s function G gravitational field

（£ —

,）

for the Dirac equation in an external

〃廿▽ * j — mj = 0

as a solution of the equation

^7 ^m V _m G （ £ — £ ） — mG （ £ — £ ） = 6 （ £ — :£ ） ,

（2）

where 7 丛 = 7 （ & ）气） ， 必） is an orthonormal tetrad.

To characterize the gravitational field let us define the operator Г by the equality

Then equation (2) can be rewritten as

1^ (^^ ^ _O^ G ( £ — X ) + i T G ( £ — T ) — mG ( £ — x )

(X —

X).

This equation can be represented in the integral form

G ( X — X ) = Go ( X — X ) + i / G ( X — X ) 「 ( x ) Go ( X — X ) J — g ( x 〃 )d ⁴ x ,       (3)

where g ( X ) is a determinant of the matrix ( g *” ) . It is possible to verify the validity of (3) by acting on the left and right parts of the equality (3) with the operator

i )( H ) V oH + i r ( X ) — m.

In the case when the gravitational disturbance is small, it is possible to solve the equation (3) by applying the method of successive approximations and find the Green’s function in the form of a series:

G ( X — X ) = Go ( X — X ) + i / Go ( x — X ) 「 ( x ) Go ( x — X ) J — g (x 〃 ) d ⁴ X +

+ i ² / Go ( x — x ‘‘‘ ) r ( X ’’’ ) Go ( X ’’’ — x 〃 ) Г ( x“ ) Go ( x 〃 一 x ‘ ) J — g ( X ’’’ ) J — g ( x 〃 ) d ⁴ x ’’’ d ⁴ x 〃 + ... .

• B.    Dirac Integral Equation

The following theorem is valid: Let a gravitational field be given in which the Green’s function G (x ‘ — X ) can be expressed as a uniformly convergent series ⑷ .Then at an arbitrary point x ‘ of the space-time region bounded by the closed hypersurface E the bispinor describing the motion of an electron in this field can be represented as

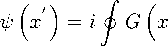
— x)t*(x)3(x) J — g ( x ) dS p. ,

where J ... ，一 g ( x ) dS m is the integral over the closed three-dimensional hypersurface E .

To prove the theorem let us first prove two auxiliary lemmas:

Lemma 1. The equality is valid:

哪一47а:M7"俨一卜")〜;"=О, where T入屮=Vm7a is the covariant derivative of)*

Proof. It is known that

7 入廿『 = 一 2 廿 .

Let us take the covariant derivative of both sides of this equality

7a ； m7 " ) "  + ) х 噓『+ ) х 俨喻= ^-2 圖.                    ⑹

Considering the equality

俨旷+『俨=2g"x let us rewrite (6) in the form

7 а ； Д ( 2 g "" ^-『廿) + 7 A 7^7 " + (2 改 一 7 ^m 7a) 脸 = ^{- 2} 哪.

From where

6 ) 勺 一 7a ； m7 “ 俨 一 7 ^м 7 ^А 7а ； м + 7 А 7^7 “ = 0 .

Since

"次=7A 喝;J⑷)旷=-2%； J(。)= -2蹴， we get

⁴ 哪 - 7 А ； д 7 ^Л 7 ^{м -} 7 ^м 7 ^Л 7 А ； д = ° -

Q.E.D.

Lemma 2. For the Green’s function G ^ x — £ ) the following equality is valid:

7 ( ⁰ ) G ⁺ ( x — x ‘ ) 7 ⁽⁰⁾ = G ( x ‘ — x ) -

Proof. From the equality

7(0)7 3)+7(°)= 7(h), for the operators of the form / = 7⑷ 丄 follows

7(0)舒7(0)=@                                ⑺ and for the multiplication of operators follows

7 ( 0 ) 0 后 0 ) ⁺ 7 ( ° ) = 7 ( ° ) 0 + 7 ( ° ) 7 ⑼石 + 7 ( 0 ) 7 ⑼ Х + 7 ( 0 ) = 0 石 2               ⑻

Let us substitute the series (4) into the

convergence of series (4) and using (7) and (8) we obtain

expression 7 ⁽⁰⁾ G ⁺ (x - x‘)

7 ( ⁰ )

Given the uniform

7 ⁽⁰⁾ G ⁺ ( x — x ) 7 ⁽⁰⁾ = G ( x — x )-                             ⑼

Here the sign of the argument changes because the sign of the exponent changes at the complex conjugation (1).

Q.E.D.

Proof of the theorem. Consider 4-vector

F " = G ( x — x ) 7 “ ( x ) 3 ( x ) .                                  (10)

Let us calculate the covariant derivative of this 4-vector

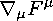
乙 F " + r%F " = "G d —^x ) 7 " ( x ) 帆 x ) + ^G ( x — x ‘ ) ^д^ 帆 x )+

+ ^G ( ^{x — x} ‘ ) 7 " ^{( x )} ^d^E l + ^G ( ^{x — x} ‘ ) ^r "“ 7 " (^x.( ^{x )}

= T « ▽ " & • 7 " 砂 + G • І7 “ ▽ " 叫 + G ( V" 7 " — Г " 7 " — 7 " Г ") 我

Here spinor connections have the form

• ¹ A                1 入

• ^г " = 4 ^{7 7} 入屮 ， ^г " = 4 ⁷ % ; " ^{7 -}

• Then given lemma 1 we obtain

• V " F " ( x ) = 〃 7 ⁽⁰⁾ 6 ( x — x ) ^ ( т ) .

  
  

Substituting (10) and (11) into Gauss’ formula

/ V" F " ^—gd ⁴ x = У

F" Cd”

we obtain

j ( £ ) = — 〃 / T ( ⁰ ) G ( 审— т ^ 7 ^м (х)^ф(х) ^ — <7 ( т ) ć/S*_m .

By using lemma 2 it is possible to transform the equation (12) into the following form:

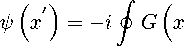
— т^ 7 ^м ( т ) ^ ( т ) ^— ^ (^仍 屮

Q.E.D.

The closed 3-surface over which integration is performed (5) consists of infinitely distant timelike 3-surfaces and spacelike 3-surfaces t = 力 1 and t = 厶 (力 i < 厶) .The Green’s function in spacelike directions decreases to zero at infinity. Therefore, the integrals on timelike 3-surfaces will be equal to zero. Then given that

7 “ У— ^d” = ]"^—П " dS = ±7 ^м ^—де^ dS = ±7 ^{( а}} ^—gdS, we represent the equation (5) in the form

j (g) = 〃/ G ( £ 2 — £ i ) 7 ( ⁰ ) j ( T i ) 7 —g ( £ 1 ) d³x i — i // G ( £ 2 — £ 1 ) 7 ⁽⁰⁾ j ( £ 1 ) J - g ( £ ； ) d ³ £ i .  (13)

The first summand corresponds to electrons with positive energy, and the second summand corresponds to electrons with negative energy. In this form the equation has a more universal character. It can be used not only for the Born approximation, but also in solving the particle scattering problem by the method of Feynman diagrams. In addition, the equation allows a visual interpretation. The Green’s function determines the amplitude of the transition of the electron from the initial state with the wave function j ( £ 1 ) to the state with the wave function j ( £ 2 ) under the influence of the gravitational field.

• C.    Born Approximation

Let the gravitational field be central and stationary. Then we have j(£)= j (r) е-i£t, where £ is the energy of an electron. In this paper the case of interest is that the function j (r) at r Ta has the form of a superposition of plane and spherical divergent waves eipr j (r)〜ие2Р0т + / (n)---,

r where po and p are electron momenta before and after scattering at infinity; u is a bispinor describing the state of an electron with momentum po; n = ^. Let the initial state of the electron be described by a plane wave j (£1) = ueiB—P。吟.

Let us substitute (4) into the first summand of equation (13). Let us restrict ourselves to the first approximation. Then after the transformations known from quantum mechanics [26, 27], we obtain the bispinor A ( n ) in the form

/ ( n ) = i j ( — 7 • p + 7 ( ⁰ ) £ + m ) / г ( r ) ие ^гКг d ³ r ,                   (14)

where К = po — p . Here the function Г ( r ) is defined from the equality

Гие^{-г(еі-Р0Г}) = Г( г ) ueig—PQ 吟.

Choosing the normalization in the form Uu = 2 m, U7 ^M u = 2 P ^M [28], we find the scattering amplitude and differential cross section for scattering of electrons which possess polarization s in the final state in the form

% 0₂m4 ^A ⑺ ,

d ( J _s = £ ( n )| 2 d C ,

where U s is a bispinor describing the state of elastically scattered electrons on a wormhole with momentum p = p on and polarization s, d C is the solid angle element having direction n .

Given that Us ( — 7 • p + 7 ⁽⁰⁾ £ - m) = 0 ,, from (14) and (15) we obtain

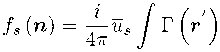
Ue^{i Kr ，} d ³r' .

By substituting this expression into the (16) and averaging the differential scattering cross section over the polarization states, we obtain it in the form do = В (n) usQ$B (n) dC, where В (n)=泰 / Г ^ r'^uelKr d3/; the line above UsUs means averaging along the direction of vector n. It can be shown that the density matrix of electrons which are scattered by the solid angle element dC,

夕 ( n ) = U s ( n ) U s ( n )

and the density matrix of electrons for the incident flux po = uU are equal. This means that the fraction of electrons of a certain polarization which are scattered in the direction of the vector n is equal to the fraction of electrons of the same polarization in the incident flux. Then for the differential cross section for scattering we have do = В (n) uUB (n) dC.

From where we find that the scattering amplitude of the electron is equal to

/ ^{( n )} = ^{uB ( n )}

jU / Г ( r ^ие^гКг d ³ r .

• D.    Electron Scattering on an Ellis-Bronnikov Wormhole

As a scattering center we choose the Ellis-Bronnikov wormhole, the metric of which has the following form ds2 = d产-^^2 - M (de2 + sin2 e d,)                      (18)

1 ― T2

where 冗 is the radius of the throat. In spite of the fact that in spacetime with metric (18) there is no gravitation, the scattering on such a wormhole can be described by the above formulas. To find the operator Г let us write out the nonzero components of the Christoffel symbols for the metric (17):

^Г 1і = ― 「 3 二£ 2 ， ^Г ； 2 = ^{- Г} ― | 2 ) ， ^Г 3з = ^{- Г sin} 2 ^e ° ― | 2 ) ，

^Г І2 = 「, ^Г 3з = — ^s 〃^ ^e co^{se, Г} 3з = 「, ^Г 2з = Eg 仇              (19)

and also choose the orthonormal tetrad in the form

= a^g (^П ? ； ¹ ".

Substituting (19) and (20) into the expression for spinor connection

Г“ = 4 eme(c)x；^7(b))(°), we find that all its components are equal to zero. Then assuming R is small, for the operator Г we get

Γ

1 "2

2 '   r ² dr

Then from (17) we obtain the scattering amplitude in the form

/S) = 4 亓R2po / cos^e'Kr d3r , where q

(\, \ o ), 丁 ‘ is the radius-vector of an arbitrary point. The integration is performed over

such points. The angle q is equal to

穴 q =—

- j - ",where “ = ( \ ) .

Writing down the result of the integration as a series and leaving only the terms that give the summands containing the sixth degree R 6 and below for the total cross section for elastic scattering, we obtain

/ S) = - 4 ^{R 3 P} 0 ^cos 2 + 2 ^{R 2 P} o ( 1 - 3 ^{R 2 P} 0 ^sin 2 2 ) .

As a result, we obtain the total cross section for elastic scattering in the form

° el

亓 R 4 p 0 + 2 亓 ( | б - 3 ) R ⁶ p 0 .

From the optical theorem

° tot

4тг

—• Imf (0).

Po we find that the total cross section for scattering is equal to

° tot

2ttR ² .

Then the total cross section for inelastic scattering has the form

6nei = 2开R2 -亓R4po - 2亓(% - 3) R6p4, and the fraction of inelastically scattered electrons is equal to

内 nel

Aot

It follows that at Rp o ^ 1 , 0923

• ¹    - 2 ^{R 2 p 0} - ( T 6 - 3 ) ^{R 4 p} 0 .

electron scattering will be completely elastic, and when the condition Rpo > 1, 0923 is satisfied, the total cross section for inelastic scattering becomes negative.

Conclusion

Within the framework of the approximations used, the following statements can be made:

• 1.    There is no total absorption of electrons by the wormhole. The existence of inelastic reaction channels necessarily entails the existence of elastic scattering.

• 2.    There is a condition on the size of the throat R and on the value of the initial electron momentum p o , at which the flux of electrons will be completely scattered elastically.

• 3.    There is a condition on the size of the throat R and on the value of the initial electron momentum p o , at which the total cross section for inelastic scattering becomes negative. The Born approximation used in this study restricts the inelastic scattering channels. The electron creation processes in this problem can be excluded. Therefore, there remains only one possibility to increase the number of elastically scattered electrons which exceeds the number of electrons in the initial flux. Additional electrons can appear only as a result of transition of electrons through the wormhole from the region of space located on the opposite side of the wormhole. Thus, it is possible to create such a flow directed to the wormhole which will create a “negative pressure” in the region containing the wormhole. Perhaps wormholes can be stabilized without exotic matter in this way.