Electrooptical response of the films of polymer dispersed nematic with conical boundary conditions

Introduction. Films of polymer-dispersed liquid crystal (PDLC) consist of liquid crystal droplets dispersed into a polymer matrix [1; 2]. Recently, much attention has been paid to LC composites due to their wide application possibilities in electro-optical devices, such as smart windows, optical sensors, flexible information display devices, etc.[3; 4]. New composite materials with improved optical characteristics and reduced control voltages are being developed [5; 6] . The optical properties of such materials depend on the initial configuration of the director (a unit vector oriented along the long axes of the liquid crystal molecules) formed in the droplets, which is changed by the influence of external factors (unidirectional stretching of the film [7–9], temperature changes [10] , application of an electric field [3]). This fact gives the opportunity to control the light transmission of the entire film. Thus, in the initial state, the gradient of the refractive indices between the polymer matrix n p and the unusual refractive index of the liquid crystal n e leads to intense light scattering of the incident light. When the electric field directed perpendicular to the sample plane is switched on, the LC director is oriented along the field, and the film passes into a transparent state, in case that the refractive index of the polymer n p is equal to the ordinary refractive index of the LC n o .

To date, the electro-optical response of PDLC films in which the director at the interface is oriented perpendicular (homeotropic boundary conditions) [11] and parallel [12; 13] (tangential boundary conditions) to the droplet surface has been well studied. The voltages required to switch PDLC films with such boundary conditions to a transparent state are currently tens and hundreds of volts, which is significantly higher than the values required for modern LC devices. There are various ways to improve the electro-optical characteristics of LC composites, for example, when adding a dichroic dye to the LC (guest-host effect), the contrast ratio of the samples increases, while the control fields do not change [11] .

In this paper, [5; 6]the introduction of a chiral additive and a photo-crosslinking polymer into the LC made it possible to reduce the control fields.

In PDLC films in which conic boundary conditions are set for the nematic (the director at the interphase boundary of the droplets is oriented at an angle of 40 to the normal to the surface), an axial-bipolar configuration of the director [14] is formed . Droplets with such a configuration under the action of an electric field tend to orient the axis of symmetry along the applied field, and the process of reorientation of the axis of symmetry is of a threshold nature. In this case, the threshold field is several times smaller than the threshold field required for reorientation of similar droplets with a bipolar orientation structure, which is formed under tangential boundary conditions [15] . However, the macroscopic optical properties of PDLC films with conical boundary conditions and their changes under the influence of an electric field have not been practically studied to date.

This paper studies the electro-optical response of PDLC films with nematic droplets having an axial-bipolar orientation structure of the director field in the case when the electric field is applied perpendicular to the film plane.

Materials and methods. The PDLC of a film based on a nematic mixture of LN-396 (Belarusian State Technological University) dispersed in a polymer matrix, used as polyisobutyl methacrylate (PiBMA) (Sigma), was studied. The samples were made using a mixed SIPS and TIPS [2; 16] technology with a weight ratio of LN-396 : PiBMA = 60: 40. In the first step, a homogeneous nematic/polymer/ethyl acetate mixture was applied to a glass substrate coated with an ITO electrode and dried until the ethyl acetate solvent was completely removed. As a result, the phase separation and formation of the composite PDLC film took place. Further, on the part of the substrate not covered with a composite film, teflon spacers were located. Spacers with a thickness of 5, 10, 20, or 30 microns were used to obtain samples with different thicknesses of the PDLC film. The composite film and teflon spacers were covered with a second glass plate with a transparent ITO electrode, and the resulting cell was placed under a press, heated to 70°C and was kept at this temperature for 30 minutes. After heating, the above-described cell was removed from the press and cooled to room temperature for 1 min.

The study of the electro-optical response was carried out on a typical installation. A beam from a He-Ne laser (Linos) with a wavelength of λ = 632.8 nm was used as a radiation source. The transmittance of the PDLC films was measured using a PDA100A-EC silicon photodetector (Thorlabs). The signal from the photodetector was recorded with a digital multimeter 34465A (KEYSIGHT Technologies). The radiation scattered on the samples was delayed by a diaphragm with an angular size of 50 minutes, which allowed only directly transmitted light to be recorded. An alternating voltage with a frequency of 1 kHz was applied to the PDLC cell from the signal generator G3-123. The morphology of the samples and the optical textures of the nematic droplets were studied using a polarizing optical microscope (POM) AxioImager. M1m (CarlZeiss). For microscopic studies of the droplet response to the electric field, a sample with a spacer thickness of 30 microns and an average droplet size of 7.2 microns was made. To do this, at the final stage of the manufacturing process, the sample was cooled to room temperature for 60 minutes.

Electro-optical response of PDLC films. Figure 1 shows photos of a section of a composite film sample with LC droplets having an average size of 7.2 microns. In the initial state, the bipolar axes of the droplets in the entire volume of the film are oriented randomly, which contributes to the intense scattering of the radiation incident on them (Fig. 1, a). The sample was studied in unpolarized light, and it is seen that different individual droplets scatter the light differently. This effect is associated with the different orientation of the axes of symmetry of the droplet structure relative to the normal to the film plane (the direction of observation) [14]. Accordingly, the minimum scattering will be observed on droplets whose bipolar axis is parallel to the observation axis, and vice versa, the maximum scattering of light will be drops with the axis of symmetry lying in the plane of the sample. The nature of the droplet response directly depends on the orientation of the bipolar axis with respect to the applied field, which is parallel to the direction of observation. If the angle between the field and the droplet axis is different from 90°, then the response process is almost threshold-free, and even at small fields, the bipolar axis is reoriented (Fig. 1, b). At the same time, the greater the applied voltage, the stronger the droplets are oriented along the field (Fig. 1, c). Conversely, with the orthogonal orientation of the bipolar axis of the droplet in relation to the applied field, the reorientation process has a threshold character, while the beginning of the reorientation process occurs at stresses that cause almost complete reorientation of the droplets with an initially non-orthogonal orientation of the axis of symmetry (Fig. 1, d).

In the manufacture of cells for electro-optical studies, the cooling rate of the samples was higher, which contributed to a decrease in the average drop size to a value of 2.1 microns. At the same time, the initial distribution of the orientation of the bipolar axes of the droplets in the samples was similar to that described above and shown in Figure 1. Consequently, the described process of response to the electric field of the LC droplets ensemble is also appears in the electro-optical response of the samples under study.

Fig. 1. Photos of the PDLC film taken at the applied voltage U = 0 V ( a ), 5 V ( b ), 7 V ( c ), 10 V ( d )

Рис. 1. Фотографии КПЖК пленки, сделанные при приложении электрического напряжения U = 0 В ( a ), 5 В ( b ), 7 В ( c ), 10 В ( d )

The character of the response to the electric field of the LC droplet ensemble described above is also shown in the macroscopic electro-optical response of the samples under study. Figure 2, a shows the dependence of the light transmission T of the samples on the value of the applied voltage U. The light transmission T was defined as the ratio of the intensity I of the light transmitted through the sample to the intensity I0 of the incident radiation: T = (I / I0). From the dependences, it can be seen that the change in light transmission with the application of voltage is almost threshold-free. When exposed to relatively low voltages, there is a slight increase in light transmission, then there is a sharp increase in the coefficient T with an increase in U, after which the process of change slows down and goes to saturation. Thus, the transmission level of 10 % of the maximum value of the Tmax coefficient is achieved at voltages U10 = 1.8 V for a sample with a spacer thickness of 5 microns, and in a 30 microns sample U10 = 8.0 V. It can be seen that with increasing thickness of the sample d, the voltage U10 increases (Fig. 2, b), while for samples with a thickness of 10 to 30 microns, an almost linear dependence of U10(d) is observed.

For all the studied samples, low voltage values are characteristic, at which the maximum light transmission is achieved (Fig. 2). Thus, the transmission level of 90 % of T max is achieved at voltages U 90 = 4.8 V for a sample with a spacer thickness of 5 microns, and in a 30 microns sample U 90 = 12.0 V. At the same time, as the thickness of the samples d increases, the voltage U 90 increases, but the value of the ratio U 90 / d monotonically decreases with increasing d . The studied samples are characterized by a high value of the maximum transmittance. Thus, T max = 91 % for a sample with a thickness of 5 microns, and T max = 84 % for a spacer thickness of 30 microns. This allows achieving a significant value of the contrast ratio CR = T max / T min ( T min is the transmittance of the sample in the initial state), which reaches a value of 5078 for 30 microns of the sample (Fig. 2, b ). The decrease in the CR value with a decrease in d is due to the fact that in thinner samples in the initial state, the samples scatter light less intensively, which is reflected in a higher value of the T min coefficient. For example, for a 5-microns-thick PDLC film, T min = 17.4% and T min = 0.015% for a film with d = 30 microns.

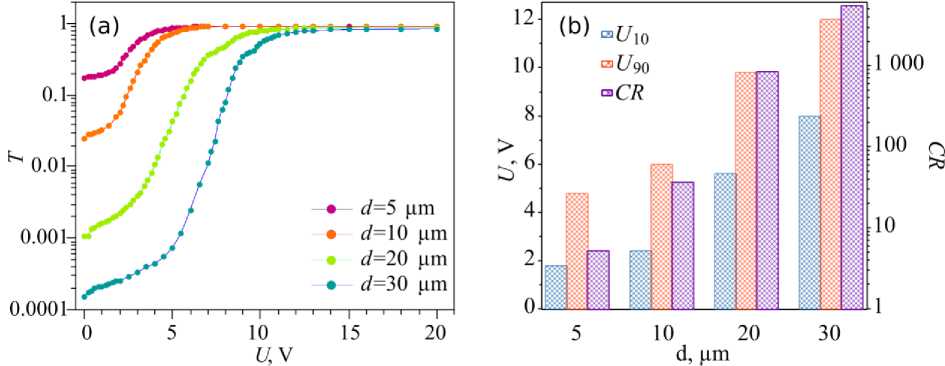
Fig. 2. Dependences of light transmittance T on applied voltage U ( a ); the voltage at T = 10 % ( U 10 ), the voltage at T = 90 % ( U 90 ), and contrast ratio ( CR ) of PDLC films with a thickness of d = 5, 10, 20 and 30 μm ( b )

Рис. 2. Зависимость светопропускания T от приложенного напряжения U ( a ); напряжение при T = 10 % ( U 10 ), напряжение при T = 90 % ( U 90 ) и коэффициент контрастности ( CR ) для КПЖК пленок толщиной d = 5, 10, 20 и 30 мкм ( b )

To analyze the light transmission of samples, the exponential dependence of the transmission coefficient T = exp(-Nσd) on the thickness d of the scattering medium is used. Here N is the density of the LC droplet arrangement; σ is the effective scattering cross-section of a single drop, depending on the ratio of the unusual refractive index of the LC ne and the polymer np, the radius of the droplets, and the wavelength of light [16] . Figure 3 shows the dependences of Tmin and Tmax on the thickness of the samples. It can be seen that the log(Tmin) dependence is close to linear for PDLC films with a spacer thickness of d from 5 to 20 microns. The deviation from this dependence for a thicker sample can be explained by a significant contribution of multiple scattering on LC droplets, which contributes to slowing down the reduction of the transmission coefficient with increasing thickness of the scattering layer. At the same time, for the log(Tmax) dependence, the opposite trend is observed for an accelerated decrease in the Tmax coefficient with an increase in d. This effect seems to be related to the complex orientation structure of the droplets scattering the radiation. For example, the presence of point and linear defects that give additional light scattering inside the droplets. This scattering is weak in the initial state, when light scattering prevails due to a significant gradient of the refractive index between the polymer and the LC. At the same time, in the saturation mode, this gradient of the refractive index becomes insignificant, and the additional contribution from scattering on the defects of the orientation structure inside the LC droplets can have a significant effect on the overall scattering pattern, and, as a result, on the transmittance of the sample Tmax.

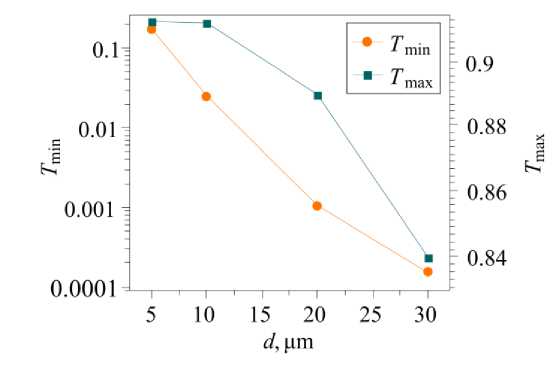
Fig. 3. Dependences of minimal ( T min ) and maximal ( T max ) light transmittance on the sample thickness d

Рис. 3. Зависимости минимальных ( T min ) и максимальных ( T max ) значений светопропускания от толщины КПЖК пленок d

Conclusion. This work presents the study on the electro-optical response of cells based on PDLC films, in which the polymer sets conical boundary conditions for a nematic liquid crystal. The process of reorientation of an ensemble of droplets with an axial-bipolar director configuration is described, and it is shown that in the initial state, the bipolar axes of the droplets are randomly oriented both in the sample plane and relative to the normal to the cell plane. As a result, there is no clear threshold in the response of the PDLC cells under study, but at low applied voltages, there are minor changes in the orientation structure of the nematic droplets and, accordingly, in the light transmission. The electro-optical response was studied for samples of PDLC films of various thicknesses, for which the dependences of the light transmittance on the applied voltage were measured. The studied samples are characterized by small control fields, but at the same time a high cell transmittance in the switched-on state and large values of the contrast ratio CR observed in samples with a thickness of 20 microns or more are achieved. The voltage U 10 is characterized by an almost inversely proportional dependence on the sample thickness d . The results obtained have shown that PDLC films with a conical coupling at the interface boundaries are promising for use as electro-optical materials with a low control voltage and a high contrast ratio.