Empirical relationship for queue length estimation in a system with fractal shot input
Автор: Trenogin N.G., Petrov M.N., Sokolov D.E.
Журнал: Сибирский аэрокосмический журнал @vestnik-sibsau
Рубрика: Математика, механика, информатика
Статья в выпуске: 2 т.18, 2017 года.
Бесплатный доступ
Traffic in modern data networks and information systems are most adequately described by different classes of fractal models. This kind of models takes into account the following key characteristics of traffic as high variability events grouping and explicit correlation structure on different time scales. Fractal shot process FSNDP, referring to the fractal point process is sufficiently accurate approximation of the network load at individual workstations or small workgroups, is defined with five numerical parameters, with known estimating algorithms on available samples (based on actual traffic dumps). Studies based on queueing system simulation with input FSNDP stream managed to establish a stable relationship between the change in each of the input parameters and the average queue length in the system. Confirmed direct correlation queue length of the parameter characterizing the amplitude of the individual load bursts, found an inverse relationship of the index related to the Hurst parameter and master degree of fractal properties. Based on the identified dependencies, obtained empirical relations between parameters of FSNDP process and the average queue length in single-channel queueing system with unlimited queue and deterministic service discipline FSNDP/D/1. These relationships allow to estimate the average volume of buffer used and the average delay introduced by the network equipment in the load conditions expressed fractal properties from measurements of real traffic. The presence of the formulae increases the importance of traffic models based on FSNPD, since it makes possible to perform a full cycle analysis of queueing systems and queueing networks without involving the simulation methods.
Fsndp, fractal traffic, fractal shot-noise driven poisson, queueing system, simulation
Короткий адрес: https://sciup.org/148177700
IDR: 148177700 | УДК: 621.396.67
Текст научной статьи Empirical relationship for queue length estimation in a system with fractal shot input
Introduction. In recent years the traffic of data communication networks, also as a part of distributed information systems, characterized by high variability and explicit correlation properties, is described by various fractal models [1–4].
Unlike geometrical fractals, determination of which is based on geometrical similarity of a part of an object to the whole, with fractal random processes – the part of a path is similar to the whole statistically: when averaging by time at various scales, the process substantially keeps values of the first and second order statistics, i. e. doesn’t smooth out, doesn’t lose variability and correlation structure.
Fractal or self-similar properties of the network traffic, revealed originally on the Ethernet networks and broadband access (BBA) in the 1990s [5; 6] explains feeble suitability of classical Markov methods and models of the queueing theory for simulation of the modern high-loaded systems and data communication networks. First of all it is about the explicit correlation structure – the phenomenon of an after-effect which by definition neglects Markov models. However, despite adequacy of traffic streams description using fractal models, receiving of expressions suitable for practical calculations for the queueing system models is connected with considerable difficulties. Several options of formulas for queueing system models with the elementary fractal sequence on the basis of fractional Brownian motion [7; 8] are known, though this flow can be considered adequate for the description of backbone segments traffic, not for distributed information systems at the level of individual workstations and small workgroups. Also there are solutions based not on specific sequence models, but on their universal statistical characteristics [9].
On the basis of simulation modeling the authors managed to receive the ratios suitable for calculation of queue volume in queueing systems with an input flow using the fractal shot process and therefore, for capacity of the appropriate fragments of packet-switching networks estimation.
Fractal shot process (FSNDP) model. According to the result of the research of the Ethernet-traffic real traces, as the authors have shown [10–12] earlier, the adequate model of packet flow in distributed system of data processing with the remote workstations, one of fractal point processes, namely the fractal shot process which is also called FSNDP (Fractal Shot Noise Driven Poisson), belonging to the category of double stochastic Poisson point processes, can be used. For the first time the model of the network traffic based on this process was suggested by S. Lowen and B. Ryu [13, 14]. For the process there are approaches to statistical parameterization on the received dumps of the real traffic, it also can be generated using the correct and moderately labor-consuming calculations within the set parameters.
Time varying rate of FSNDP process is set by the continuous accidental process – fractal shot noise which is received by filtering classical Poisson process.
FSNDP process is completely defined by five numerical parameters (µ, β, K , A , B ), having the following value.
Primary Poisson stream { ti } with constant rate µ becomes the input to a linear filter with impulse response function
Kt -e , t g ( A, B ), 0, t £ ( A , B ),
where β is defined by the level of the process selfsimilarity; A, B – non-negative cut-off parameters; K – the positive constant, determining the amplitude of total process. The filter produces the fractal shot noise ад i (t) = ^ h (t - ta,, (2) i=-ад considered as time varying rate for the second Poisson point process, which output is the FSNDP.
FSNDP process acquires steadily self-similar properties under a condition that А << B and А , close enough to zero . With practical modeling it is usually accepted that А = 0 or А = 10–7.
Parameter β is connected with Hurst parameter H , i. e. defines degree of expressiveness of fractal properties of the resultant process:
H = 3/2 -p . (3)
Hurst parameter of H is the most general characteristic of any fractal process and can accept values from an interval [0.5; 1). Value 0.5 means total absence of fractal properties, growth of H towards 1 – strengthening of expressiveness of self-similar character.
General comments on the approach to simulation modeling. Earlier, on the basis of the analysis of really operating distributed information systems network traffic dumps the fractal shot process of FSNDP was considered to be an adequate model of such traffic. Also numerous estimates of parameters of the FSNDP model on real dumps have been carried out; for generating the artificial sequences in this research the values which are close to the values characterizing some typical dumps of the real traffic [12$ 15], but rounded for simplicity were used. Values µ = 0.1, K = 10, A = 0, B = 100, β = 0.9 have been accepted as a basic set of parameters.
Earlier it has also been confirmed that the stream with constant (deterministic – D ) service rate corresponds the most to the real network load for client-server data processing system, i. e. the FSNDP/D/1 system is the most suitable for modeling. In terms and units of information transfer the volume of a packet is accepted as 100 bytes that is also close to real estimates.
The general approach to the research of influence of model parameters on the behavior of the queue is based on generating of pseudorandom sequences of FSNDP stream events with the variation of one or several parameters of rather basic set and use of these sequences as an input stream of simulation model of a single-channel server queueing system with simulated continuous time.
All generated sequences have the symbolic duration of 7200 sec. (2 hours) and volume, depending on the varied parameters, from 25 thousand prior to 450 thousand events.
Influence of process parameters on the average length of the queue. Parameter K characterizes amplitude of the resultant process’s rate bursts; therefore it is obvious that correlation between K and average queueing load ρ will be direct (fig. 1).
Simulation modeling allows to assume direct proportionality of the average queue length estimation from K.
Direct influence on the height of the curve queueing system load for β exponent; respectively, the reverse influence of Hurst parameter H connected with this indicator is determined. This result, which is steadily shown during the runs of simulation model for various values of the FSNDP parameters, in general differs from the popular conception that for the general case of the fractal traffic a higher degree of self-similarity results in larger queue fill (buffer). The cause of alternative effect for a special FSNDP case needs a future research (fig. 2).
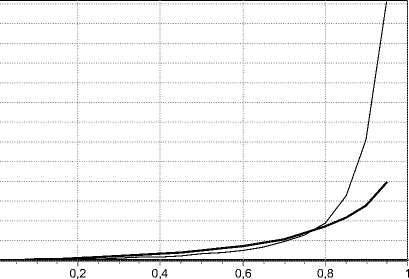
Influence of primary (auxiliary) Poisson sequence µ on characteristics of the queue length has appeared to be significantly lower than of the two above described parameters, and is demonstrated mainly in the field of high load – at ρ > 0.8. According to the earlier research, such loading at a fractal input in practice means the mode close to non-stationary, and doesn’t allow traffic and buffer parameters more or less precise estimation. Curve buffer fill for values µ, differing by factor 16 are given in fig. 3.
The only parameter of FSNDP process which influence on the queue under realistic values of the other parameters has not been revealed is B . Abcense of the explicit influence corresponds to physical sense of this value: duration of the decreasing intensity intervals, after which the cut-off is done, obviously shouldn’t have dramatic impact on queueing system behavior, comparable with the influence of other parameters.
Empirical ratios for the queue length estimation. By comparison of calculated values with the values received as a result of simulation modeling of queueing system behavior with a fractal shot input of FSNDP it is confirmed that under real values of the FSNDP parameters the estimation of the average queue length can be expressed by the ratio
q ( ρ ) = CK ρ , (4)
H 1-ρ where С – positive constat, Н – Hurst parameter connected with the process β parameter value by ratio (3).
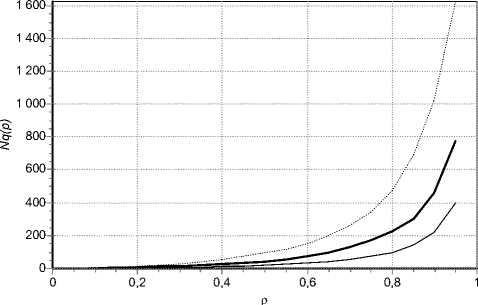
Fig. 1. The average length of the queue under parameter K variation
|
1 |
2 |
3 |
|
|
µ |
0,1 |
0,1 |
0,1 |
|
Β |
0,9 |
0,9 |
0,9 |
|
K |
10 |
5 (1/2) |
20 (X2) |
|
A |
0 |
0 |
0 |
|
B |
100 |
100 |
100 |
Рис. 1. Средняя длина очереди при варьировании параметра К
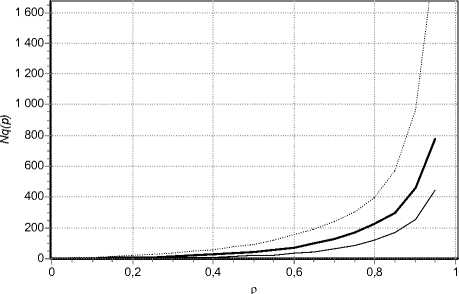
Fig. 2. The average length of the queue under parameter β variation
|
1 |
2 |
3 |
|
|
µ |
0,1 |
0,1 |
0,1 |
|
Β |
0,9 |
0,8 ▼ |
0,95 ▲ |
|
K |
10 |
10 |
10 |
|
A |
0 |
0 |
0 |
|
B |
100 |
100 |
100 |
|
H |
0,6 |
0,7 ▲ |
0,55 ▼ |
Рис. 2. Средняя длина очереди при варьировании показателя β
In the expression there are no parameters B and µ, significant effect of which on the queue under real conditions isn’t revealed in the simulation modeling. However, since µ under ρ > 0.8 can after all impact the queue length, it must be kept in mind that the queue estimation accuracy using this ratio in the queueing modes close to non-stationary mode, will decrease.
Value of the constant which equals
C = >2 (5)
in the given simulation experiments has shown rather accurate coincidence of experimental and calculated curves for various parameters of the FSNDP modeled fractal shot process.
In fig. 4. examples of curves of the buffer fill q (ρ) for parameter values µ = 0.1, K = 10, A = 0, B = 100 and β = 0.8, β = 0.9 are given, under the constant value according to the assumption (5).
It should be noticed that in the modes of minor load calculated values are slightly higher than those received by simulation modeling, i. e. the received estimation can be considered as the upper bound (fig. 4).
1 300
1 200
1 100
1 000
|
1 |
2 |
|
|
µ |
0,025 |
0,4 |
|
Β |
0,9 |
0,9 |
|
K |
10 |
10 |
|
A |
0 |
0 |
|
B |
100 |
100 |
p
Fig. 3. The average length of the queue for significantly different parameter µ
Рис. 3. Средняя длина очереди при для существенно отличающихся значений µ
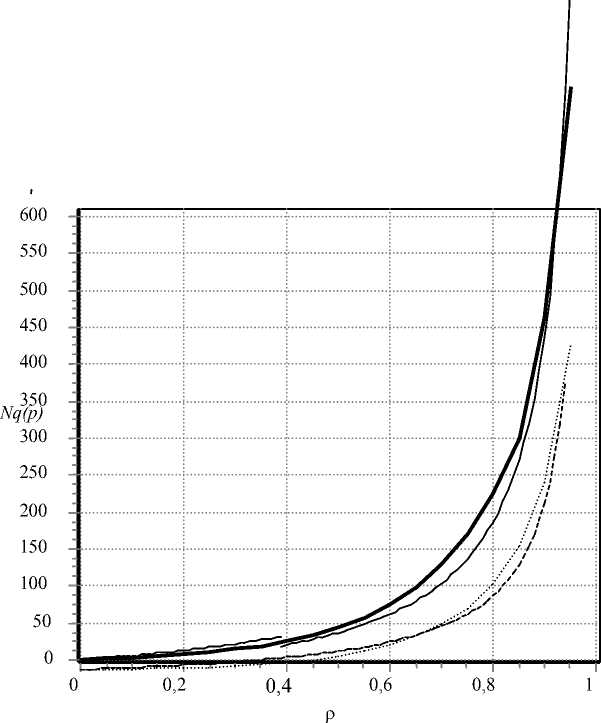
Fig. 4. Simulation and calculation curves of queue lengths under various β
0.9
0.9 (calculation)
0.8
0.8 (calculation)
Рис. 4. Имитационные и расчетные кривые длины очереди при различных β
Having combined (3), (4) and (5), it is possible to express the ratio for the average queue length estimation in single-server queueing system with fractal shot FSNDP process and determined maintenance time (FSNDP/D/1) input as:
1 K ρ q ( ρ ) = ,
2H 1-ρ
or
KρKρ =. 2(32-β)1-ρ 3-2β1-ρ
Conclusion. The offered expressions for the queue length estimation are very low resource-consuming in computation. It allows to use them both in calculation and optimization algorithms to determine throughput of data communication network elements with fractal traffic flows as well as time delays caused by these elements.
Receiving explicit ratios increases the value of the FSNDP traffic model. For this process there are ways of computer parameterization, based on available process path fragments (network traffic dumps); algorithms of the artificial sequences generating with the known parameters. Now there is also an opportunity to calculate the queue and delays in an explicit form, i. e. to carry out a full cycle of model analysis without simulation, or with the minimum use of it.
Also, there are grounds for further research, such as receiving of estimates for the queue statistical characteristics of the second order; and also development of definition methods of queueing networks with fractal flows, in particular on the basis of tensor approaches [15], based on earlier established property of keeping a flow after servicing in the system with queue.
Список литературы Empirical relationship for queue length estimation in a system with fractal shot input
- Шелухин О. И., Тенякшев А. М., Осин А. В. Фрактальные процессы в телекоммуникациях: монография. М.: Радиотехника, 2003. 480 с.
- Цыбаков Б. С. Модель телетрафика на основе самоподобного случайного процесса//Радиотехника. 1999. № 5. С. 24-31.
- Нейман В. И. Новое направление в теории теле-трафика//Электросвязь. 1998. № 7. С. 27-30.
- Нейман В. И. Самоподобные процессы и их применение в теории телетрафика//Тр. Междунар. Академии связи. 1999. № 1. С.11-15.
- On the selfsimilarnature of Ethernet traffic (extended version)/W. E. Leland //IEEE/ACM Trans. Net-working, 1994. Vol. 2 (1). P. 1-15.
- Norros I. The Management of Large Flows of Connectionless Traffic on the Basis of Self-Similar Modeling//ICC ’95, IEEE International Conference on Communications, Seattle. 1995. P. 451-455.
- Norros I. On the use of fractional Brownian motion in the theory of connectionless networks//IEEE J. Sel. Areas Commun., 1995. Vol. 13. (6). P. 953-962.
- Statistical characteristics of queue with fractional Brownian motion input/J. Chen //Electronics Letters. 2015. Vol. 51 (9). P. 699-701.
- Петров М. Н., Пономарев Д. Ю. Самоподобие в системах массового обслуживания с ограниченным буфером//Электросвязь. 2002. № 2. С. 35-39.
- Соколов Д. Е., Треногин Н. Г. Характер сетевого трафика на клиентском участке распределенной клиент-серверной системы//Информатика и проблемы телекоммуникаций: материалы Междунар. науч.-техн. конф.; СибГУТИ. Новосибирск, 2001. С. 34-35.
- Соколов Д. Е. Моделирование нагрузки в клиент-серверных системах на основе фрактальных процессов//Управляющие и вычислительные системы. Новые технологии: материалы межвузовской науч.-техн. конф.; Вологда, 2001. С. 59-60.
- Соколов Д. Е., Треногин Н. Г. Фрактальные свойства трафика в действующей двухзвенной системе обработки данных//Современные проблемы информатизации в технике и технологиях: сб. тр. Воронеж: Научная книга, 2004. Вып. 10. С. 264-265.
- Ryu B. K. Fractal Network Traffic: From Understanding to Implications: Ph. D. thesis. Columbia University, 1996. 143 p.
- Ryu B., Lowen S. Modeling, analysis and simulation of self-similar traffic using the fractal-shot-noise-driven Poisson process//Proc. IASTED Modeling and Simulation. Pittsburgh, PA, 1995. P. 1-4.
- Треногин Н. Г., Веловатый Е. А., Петров М. Н. Система поддержки операционной и бизнес-деятельности предприятия связи с использованием тензорной методологии анализа систем//Электро-связь. 2013. № 1. С. 17-20


