Empirical Study of Impact of Various Concept Drifts in Data Stream Mining Methods

Published Online December 2016 in MECS

Learning classifiers from training datasets is one of the most important steps in data mining and machine learning. Until now, many algorithms that are used for learning classifiers are based on the static environment of underlying data distribution, which remains static and does not change with time. In this scenario, the complete data can be stored in memory electronically due to which, it is possible to process the data several times.

However, in many applications, such as weather forecasting, traffic management, sensor network, etc.[3] the underlying data distribution changes very frequently, and it is usually beyond the capacity of traditional static learning algorithms to work accurately in such dynamic environment too. In the dynamic environment, the generated data exhibits the characteristics of data streams. The data streams are categorized by its frequent generation rate and big data volumes, which requires a fast response in a manner to make decisions in real time. In contrast to algorithms designed for learning in a static environment, the learning algorithms of data streams with changing concepts should require fulfilling some new constraints such as one pass testing, memory limitations and time constraints [1-2],[ 5-6].

Furthermore, in data streams the change in targeted concept with time called concept drift [4], [6] is quite often. Concept drifts occurred when the concepts represented by the continuously collected data changes with time after having a minimum stability period [3].

Fig.1. Various types of drifts in data streams

Frequent occurrences of concept drifts in the data streams decrease the performance of the classifiers significantly. The concept drifts is broadly categorized into following categories (i) sudden (ii) gradual (iii) incremental and (iv) recurring, as shown in Figure 1. In the presence of concept drifts, a good classification algorithm should be able to adapt itself to cater the changes in underlying data distribution in a manner to achieve the consistent accuracy of the classifier during classification of unseen instances that are arriving continuously with time.

Many incremental algorithms that learn incrementally over the data needed to update for every new unseen instance during learning. However, to deal with concept drifts, it is necessary for the incremental algorithm that it should ensure the forgetting of old concepts and quick adaptation to new concepts [3].

Recently, many methods have been proposed in the related literature that exclusively designed for data stream mining while considering drifting concept in the data stream. They are categorized as online learning algorithms and mainly include sliding window-based methods, ensembles, and drift detection methods. These methods fulfill the one pass requirement of learning in data stream without storing the data electronically. The online approaches can be broadly discussed in two categories: (i) Online learning approaches that use an explicit mechanism to deal with concept drifts [7], [9],[10] and (ii) Online learning approaches that do not use any explicit mechanism to deal with concept drifts [11-15][32]. Most popularly, the former online learning approaches include Early Drift Detection Method (EDDM) [7] and Drift Detection Method (DDM) [10]. The later approaches basically employ a set of learners also called ensembles are used in which each learner is assigned some weight, depending on the accuracy of learners. Ensembles are popularly used to increase the accuracy in static data problem. However, they need certain modifications to justify their applicability in datasets with changing environment. In general, consistent updating of ensemble structure and weights of learners is required for adopting the change in the environment.

Inthis paper, we present an empirical evaluation of some popular algorithms, e.g., standard Naïve Bayesian (NB), Drift Detection Method (DDM) [10], Weighted Majority Algorithm (WMA) [8], [16], Accuracy Updated Ensemble (AUE), Hoeffding Option Tree (HOT) on artificialdata stream mining with drifting concepts using datasets having four possible types of concept drifts namely: sudden, gradual, incremental, and recurring drifts.

The rest of the paper organized as follows.Section II illustrates the related terminologies and concepts related to data stream mining withconcepts drifting, this section also presents related work in the area of data,Section III describes experimental setup and datasets that we have used for empirical evaluation of algorithms. Finally, Section IV discusses theresults and section V provide the conclusion of overall empirical findings.

• II.    R ELATED W ORK

• A.    Concepts and terminologies related to data stream mining

Let (xj,yt) represents ap dimensional instance of data stream training datasetV at time t, where t represents the time such that t = 1, 2, 3,.....T and у E {C,, C2, , Cn} where Cj represents the class of data instance xj . Therefore, while considering the problem of data stream mining as the supervised incremental learning process, the task is to predict the class of new training instance (xj), if the predicted is the same as actual class of the instance, it is assumed that classifier is working well and if the prediction is wrong then updating of learning algorithm is mandatory. Such approach of training the classifiers for data stream mining isalso called Prequential method of learning. Another approach to learning is called batch learning. There are various alternates available for performing batch learning. One of the most popular approaches for batch learning is to divide the complete training dataset into equal sized data batches, such thatV = (Bt U B2 U .....U В,Д where, Bt, represents the ith batch.

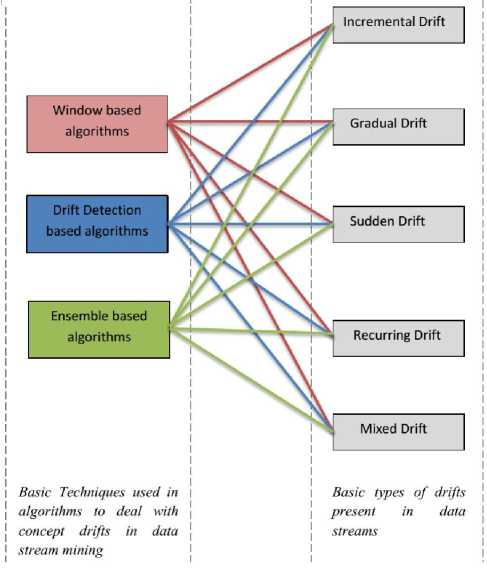
Fig.2. Various approaches for dealing with concept drifts in data streams

Concept drifts are very often in data streams, concept drifts generally occur due to change in underlying distribution, and there are many approaches described in related literature to detect the drifts [7]. As already described, the drifts can be mainly categorized into sudden, gradual, recurring and incremental. Sudden drifts occur when underlying data distribution changes suddenly, whereas in the gradual drifts, the distribution changes radically. In incremental drifts, the change in drifting concepts are very small, but persist for a long time. As a result the resultant the class change occurs completely after a long time. In the recurring type of concept drifts, the concepts keep repeating time to time.

Based on the basic techniques, which have been used in the various learning algorithms, we can alternately categorize the methods for dealing with concept drifts in data stream mining in three different categories i.e., (i) algorithms based window technique (ii) algorithms based on drift detection methods, and (iii) algorithms based on ensembles methods.

The sliding window-based approaches are very common in data stream mining [17]. In sliding windowbased methods, it is very important to decide an ideal window size. A small window size ensures the fast response to drift; however, it is very often to have false detection also. On another hand, a large window size suffers from delay in detection. For these reasons, dynamically adjusted window methods are well suited in utilizing window-based methods in data stream mining [17].

Alternately, the algorithms that employ the drift detection methods are based on the consistent statistical observation on the change in the class distribution. If any change occurs in the distribution, then base classifier is reconstructed to manage the change [18]. Drift Detection Method (DDM) [10] is one of the most popular approaches among the algorithms that uses drift detection in data stream mining. In DDM, drift detection is performed by monitoring the prediction error, which is modeled as binomial distribution. If the error rate lies beyond the decided value; an alarm is generated as an action, the current classifier is dropped and a new classifier is constructed. DDM performs well for sudden drifts comparative to the gradual and incremental.

Another approach is suggested in many kinds of literature that has been followed by the many algorithms of data stream mining is called ensemble method, which is quite apart from window and drift detection methods. Furthermore, the ensemble approaches can further be classified in approaches that incrementally learn from each coming instances one by one online and ensembles that learn in batches. Diversity among the base learners is the main issue of concern in ensemble methods; this necessity can be ensured by using online bagging [19] in which base learners are trained incrementally, and decisions of learners are combined using majority weights. Leveraging bagging [20] adds more randomization to the bagging method. The DDD algorithm  [21]analyzes  the effect of diversity in ensembles by combining four different diverse ensembles.

• B.    Description of evaluated algorithms

This section presents the description of all algorithms, which we have used for performing our analysis on various types of concept drifts.

• i.    Naïve Bayesian (NB)

NB classifiers are one of the most popular probabilistic classifiers based on Bayes theorem [22], [23], [24].The inherited property of NB makes it a good streaming method which suits well dynamic environment though its success in ensemble technique is in [11].

• ii.    Drift Detection Method (DDM)

Drift Detection Method (DDM) [11], as mentioned above is based on drift detection, when a drift is detected the system rebuild itself to incorporate the change in the concept. In DDM, the occurrence of drift is traced by monitoring the classification error rate. When the classification error rate reached to the threshold level, the system drops the previous concept and reset itself to learn the new concept.

The DDM uses the Binomial Distribution to model the error in classification. The standard deviation st ,for each point t, is given in equation (1) using probability of misclassification (pt)

St=√Pt(1-Pt )⁄ t

The standard deviation ^mi and minimum error rate Pmi achieved are stored in and DDM, then checks for following conditions:

• (i)    if Pt + st ≥ Pmin + 2 ^min warning level is triggered ․

• (ii)    if 3t + st ≥ Pmi +3 x /      L      LI- iilLilHLLiL

concept drift is supposed to be true (3)

The model made by the learning method is rebuilt, and a new model is learned in case (ii) using the stored examples since the warning level occurred.

• iii.    Weighted Majority (WM)

In machine learning, the WM algorithm [8] is one of the best meta-learning algorithms that is used for ensemble construction. In WM algorithm, each member of the ensemble is initially assigned the weight of 1 and for every mistake in classification by any member, the weight of the corresponding members decreases by the multiplicative constant factor of p , where the value of p is(0 ≤ p <1).

• iv.    Hoeffding option tree(HOT)

Decision tree based classifiers are relatively fast as compared to other model of classifications. The Hoeffding Tree (HT)[26] is an incremental classifier used for very fast and massive data streams. The HT uses only small subset of training dataset to find the best split. The number of examples required for this is decided by Hoeffding Bound. Very Fast Decision Tree (VDFT) is an upgraded version of HT that is having refinements on issues like ties, memory, computation on split function, poor attributes and initialization. Hoeffding Option Tree (HOT) [25] is another variation of decision tree.

• v.    Accuracy updated ensemble (AUE)

Accuracy Updated Ensemble (AUE) [31], is an extension of AWE. AUE uses online component classifiers, which is updated according to the present distribution. In AUE, additional modification in weight function has done to solve the problem with AWE. AUE is more accurate than AWE but required more time and memory

• III.    E XPERIMENTAL S ETUP AND E VALUATION

All experiments are performed using Massive Online Analysis (MOA) [30] framework, where each algorithm is implemented using Java language. The complete experiments were conducted on five different artificial datasets. These datasets are collected from UCI repository, and they are considered as the benchmark for analyzing the data streams. A brief description of the collected datasets is given below in Table 1.

Description of collected datasets

We collected five artificial datasets from UCI repository [29], the collection of the datasets were made in a manner such that each dataset must have any one of the concept drift namely incremental, gradual, sudden, recurring and mixed. The selection is made in this manner to have a proper analysis of various data stream mining algorithms.

Hyperplane: Hyperplane is one of most popular dataset generator used for analysis of many algorithms of data mining [27]. The hyperplane generator is generally used for generation of incremental concept drift. For our experiment, we have set the hyperplane generator to generate 1 million instances of two classes with 10 attributes and one drift only. Please refer to Table 1.

Radial Basis Function (RBF): The RBF is the very popular function that has been used in many machine algorithms. Basically, the RBF produces the real values based on a distance called centroid, which is the distance from the origin. The RBF produces drifting centroid based on the user input. For our experiments, we have generated 1 million datasets of using RBF generators to produce gradual drifts. Our dataset of RBF is having 20 attributes, 4 drifts and 4 classes as shown in Table 1.

Streaming Ensemble Algorithm (SEA): For generating sudden drift, we used SEA. A total of 1 million instances were generated with 3 attributes, 4 classes, and 9 drfits. We used MOA to generate this dataset. Please refer to Table 1.

Tree: In our experiment we have used the tree dataset, which contains four recurring drifts consistently scattered over 0.1 million instances. Our tree dataset contains 10 attributes, 15 drifts, and 6 classes.

Light Emitting Diodes (LED): The LED dataset consists of 24 binary attributes, which defines the digit to displayed over seven-segment display. We used LED function to generate mixed drifts distributed over 1 million instances with 3 drifts and 10 classes.

Table 1. Artificial datasets used for experiment

Types of Drift	Artificial Dataset Generators	No. of Instances in millions	No. of Attr ibut es	No. of Drift s	No. of classe s
Incremental	Hyperplane	1	10	1	2
Gradual	Radial Basis Function	1	20	4	4
Sudden	SEA	1	3	9	4
Recurring	Tree	0.1	10	15	6
Mixed	LED	1	24	3	10

Evaluation

All experiments were performed on Massive Online Analysis (MOA) framework, where each algorithm is implemented using JAVA. The experiments carried out on Intel Core i3 (1.8Ghz, 3 MB L3 cache, with 4 GB RAM).

We have conducted the experiments for obtaining three well-known performance measures used for measuring goodness of data stream mining algorithms. These three measures are described below:-

• 1.    Prequential Accuracy: The prequential accuracy [28], is the average accuracy of predicting the class of a new instance without learning it, based on the knowledge learned by the previously learned instances. The average prequential accuracy is calculated for a decided window size by taking an average of correctly classified instances in that window.

• 2.    Kappa Statics: Kappa Statics measures the homogeneity among the experts. Homogeneity is inversely related to the diversity of the experts i.e. more the homogeneity less the diversity among the experts.

Evaluation Time: Evaluation time is the average time taken by CPU for testing the new instance and training the classifier.

• IV.    R ESULTS A NALYSIS

As mentioned in section I, we have conducted the experiments for five different types of algorithm based on three different approaches as shown in figure 2. The graph of figure 3-7 shows the prequential accuracy of all these five algorithms on five different types of datasets that differ in the nature in the drifts respectively.

From our experiments, we observed that for incremental type of drifts all algorithms performed very well with the best performance given by DDM and WM with more than 90% average prequential accuracy as depicted in the graph of figure 3. The graph of figure 4, depicts the prequential accuracies of all five algorithms on gradually drifting dataset generated by radial basis function (RBF). It is very clear from the graphs of figure 4, that AUE is performing extraordinarily with average prequential accuracy of more than 93%, while on other hand the DDM and NB perform worst with average prequential accuracy of approx. 73%. However, the HOT and WM perform comparatively well with the average prequential accuracy of 90.49% and 89.46 % respectively.

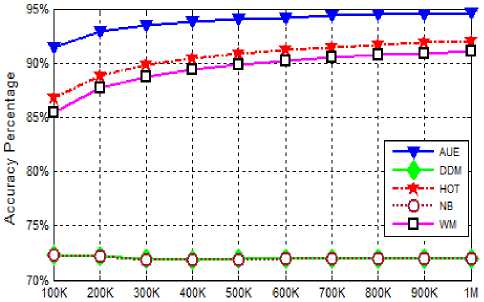
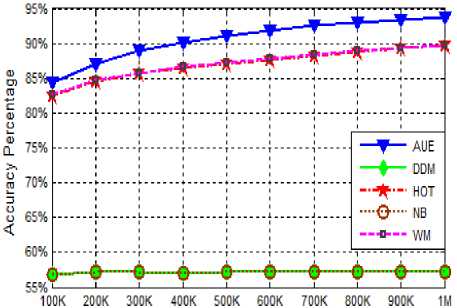
The average prequential of all algorithms for SEA dataset are depicted by the graphs in the figure 5. As we know that the SEA dataset distribution represents the sudden drift, therefore from the graphs it can be easily concluded that the AUE algorithm produces the best prequential accuracy of 89.50 % , which is just followed by other algorithms with a very small difference. Similarly, in the case of Tree dataset (recurring drift), as shown in figure 6, AUE supersedes all other algorithms with the average prequential accuracy of 90.6 % just followed by HOT and WM. However, the performance of the DDM and NB is very low (57.5 %) for the recurring dataset. All algorithms have shown a comparable performance.

The prequential accuracy of various algorithms in mixed drift dataset is shown in figure 7. From the graphs of the various algorithms in the figure 7, is can be easily determined that all algorithms are performing mediocre with the average prequential accuracy ranges between 7374 % for all algorithms. The average prequential accuracy of various algorithms on various types of datasets is summarized in Table 2. From the table, it can be observed that DDM and NB give the worst performance among the complete experiments for recurring drift dataset. The bar graph in figure 8 and figure 9, depicts the average prequential accuracy of algorithms on different datasets and average prequential accuracy of different algorithms on same dataset respectively.

Consistent performers

However, AUT, HOT and WM are performing more consistent as compared to NB and DDM.

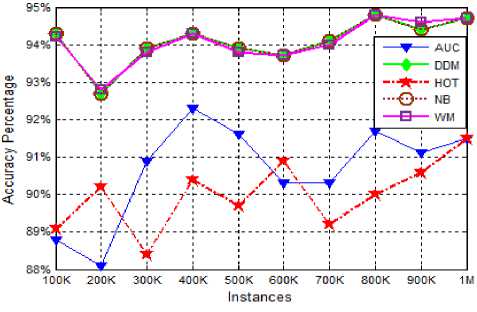
Fig.3. Prequential Accuracy on Hyperplane (Incremental) dataset

Instances

Fig.4.Prequential Accuracy on RBF (gradually drifting) dataset

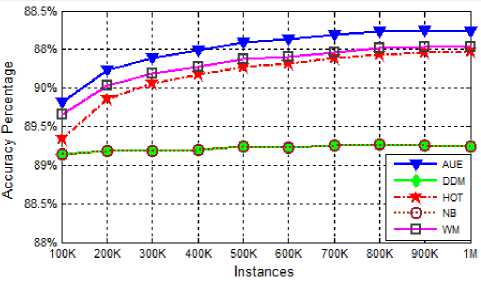
Fig.5. Prequential Accuracy on SEA (Suddenly drifting) dataset

Instances

Fig.6.Prequential Accuracy on Tree (Recurring) dataset

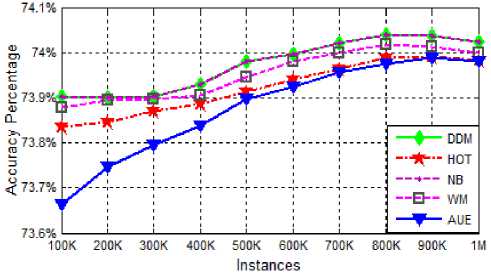
Fig.7. Prequential Accuracy on LED (Mixed Drift) dataset

Table 2. Average Prequential Accuracy

Dataset \Algo.	AUE	DDM	HOT	NB	WM
Incremental (Hyperplane)	90.5	93.98	89.53	93.98	93.94
Gradual Drift (RBF)	93.14	72.03	90.49	72.02	89.46
Sudden Drift (SEA)	89.50	88.22	89.18	88.22	89.30
Recurring Drift (Tree)	90.64	57.12	86.99	57.12	87.11
Mixed Drift LED	73.88	73.97	73.92	73.97	73.95

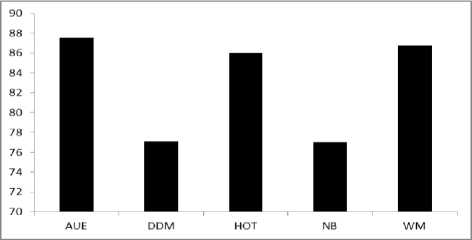
Fig.8.Average prequential accuracy of algorithms on different datasets.

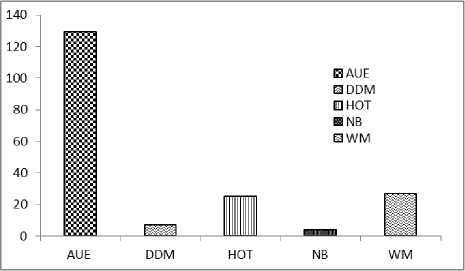
Fig.12. Average CPU time elapsed in seconds for various algorithms on various types of drifting datasets

Table 3. CPU Time elapsed in Seconds

Algo/Datasets	Hyperplane	RBF	SEA	Tree	LED
AUE	160.78	138.64	56.98	191.02	99.11
DDM	6.59	8.5	2.39	12.38	5.25
HOT	18.5	29.48	13.44	36.27	28.14
NB	3.8	5.81	1.42	6.41	2.77
WM	28.8	31.47	11.19	43.16	19.89

100 п

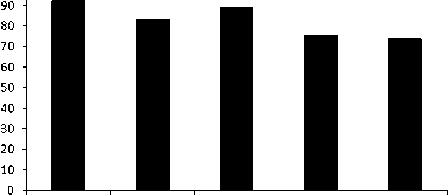
Incremental Gradual Drift Sudden Drift Recurring Drift Mixed Drift

Drift (RBF)           (SEA) (Tree) (LED)

(Hyperplane)

Fig.9. Average prequential accuracy of different algorithms on same dataset.

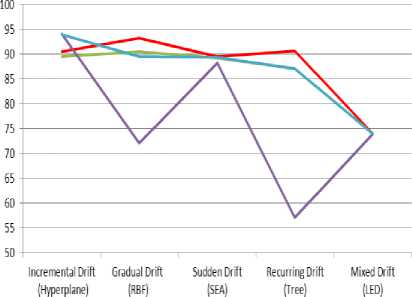
Fig.10. Consistent performance evaluation

---ADE

---ODM

— HOT

---NB

--WM

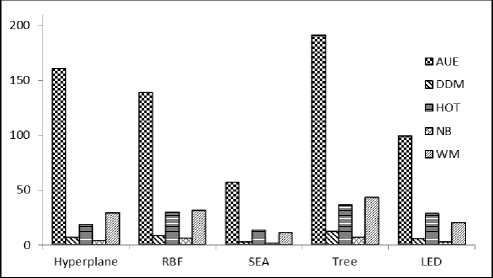
Fig.11. CPU time elapsed in seconds for various algorithms on various types of drifting datasets

Training Speed of various algorithms

The CPU time required by an algorithm is very crucial performance measure for determining the goodness of the algorithm in data stream mining of drifting streams. Drift detection delay is an important factor for any algorithm for reacting upon drifts. A large drift detection time ensures more accuracy whereas the small drift detection time reduces the response time but increases the possibilities of errors in classification and hence reduces the accuracy of the system.

Ideally, a data stream mining algorithm must have small drift detection time with high accuracy. However, the nature of drifts on which algorithm has been trained is also a matter of great consideration.

The CPU time elapsed for various algorithms for various types of drifting datasets in our experiments is depicted by the bar chart of figure 11 and the average time required by an algorithm on the all datasets is given in figure 12. From the bar chart, it can be observed that the AUE algorithm is taking largest CPU time. However, the CPU time required by NB and DDM is very less and almost minimum among all. The AUE algorithm has taken about the largest CPU time of 191.02 seconds for learning in recurring (tree) dataset and minimum training time of 56.98 seconds on sudden (SEA) drifting datasets. The algorithms HOT and WM performed quite mediocre as compared to others. The CPU time (elapsed in seconds) of various algorithms on various types of datasets is summarized in Table 3.

Kappa statistics

As already described the Kappa Statistics measures the homogeneity among the experts. Homogeneity is inversely related to the diversity of the experts i.e. more the homogeneity less the diversity among the experts. The Kappa statics percentage of AUE, DDM, HOT, NB and WM are shown in figure 13 and 14 for RBF and Tree datasets respectively.

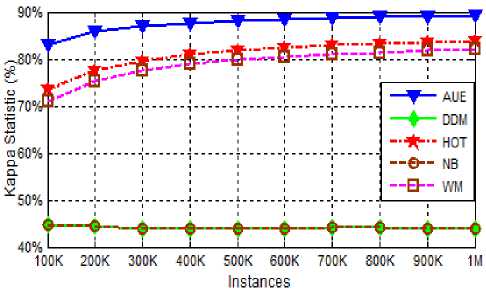
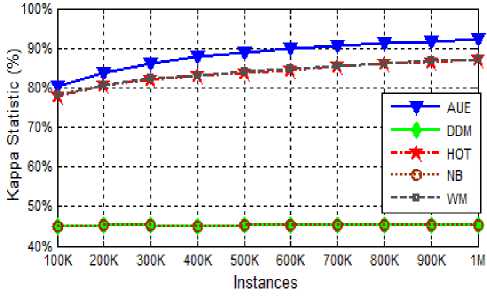
Fig.14. Kappa statistics of various algorithms on Tree dataset.

• V.    C ONCLUSION AND F UTURE S COPE

In our experiments, we examined five different data stream mining algorithms on five differently drifting datasets. From our experiments, we have observed that no algorithm is performing uniformly on the categories of the drifting datasets on which we conducted the experiments. It is very crucial for data stream mining algorithms to be very fast in detecting the drifts and reset the system appropriately in the response of the change in data distribution. However, in our experiments we observed that it is quite difficult to maintain a tradeoff between accuracy and CPU time. Moreover, it is also observed that no algorithm is uniformly accurate on all kinds of drifting datasets. Therefore, it is still very challenging task to device an algorithm, which is not only highly and uniformly accurate on every kind of drifts but also fast enough so that it can be compatible with realtime decision making system.