Employing Fuzzy-Histogram Equalization to Combat Illumination Invariance in Face Recognition Systems

Published Online August 2012 in MECS

Particle The continuous acceptance and growing use of face recognition systems in everyday life has made it a subject of intense research over the years, this is unsurprising because it possesses the merits of both high accuracy and low intrusiveness. A typical application is to identify or verify the person of a given face in still or video images [1]. Several face recognition algorithms have been proposed by researchers, these includes Principal Component Analysis, Local Feature Analysis, Linear discriminant analysis and Fisher face which are all based on dimensionality reduction. Also neural networks, elastic bunch graph theory, 3D morphable models and multiresolution analysis are some other techniques usually used to mention a few. Each of these have typically overcome the shortcomings of one another and thus extending the application areas for face recognition systems. The important applications of face recognition are in areas of biometrics i.e. computer security and human computer interaction [2].

Most of the existing researches have focused on making face recognition systems robust and invariants to light intensities, pose of subjects, expressions on the faces of subjects and other details like backgrounds and noise. Specifically, the problem of illumination effects on face recognition has been a major concern. However, there is not yet a complete solution to this intriguing problem in face recognition systems.

The problem of illumination effect becomes obvious when the system is being trained with images that are more (or less) exposed to light and then being compared to probe images taken under different intensities of light with respect to the angles of lighting i.e. the horizontal and vertical planes. Typically, this kind of differences in lighting makes no difference to the human vision perception and recognition capabilities; however, computers see this type of images as different images even if they contain images of the same subject. Since some features are hardly detectable by eye in an image, we usually try to enhance these features. Histogram equalization [3], [4] is one of the most well-known methods for contrast enhancement.

Histogram equalization accomplishes this by effectively spreading out the most frequent intensity values. It is very useful in images with backgrounds and foregrounds that are both bright or both dark. However, since histogram equalization makes use of global statistical information of the image, it is not capable of diagnosing the local variations [9]. These local variations usually called “edge” are important features of the image which when enhanced, can result in enhancement of the entire image. Also, with Histogram equalization, it is difficult to control the enhancement result in practice and all image histogram is equally equalized e.g. for the area with low-gray-frequency, contrast will be weakened or eliminated, that is to say, noise may be magnified. Thus, if ordinary histogram equalization is directly used to normalize light intensity of an image, the background gray levels and noise will be strengthened. On the contrary, target gray levels will be lacked. It may enhance background and noise and reduce the target and details contrast. Sometimes the over-bright phenomenon [5] may come out. Therefore, traditional histogram equalization algorithm is not ultimately suitable for illumination normalization in face recognition systems.

This paper proposes employing fuzzy histogram equalization in combating illumination invariance in face recognition systems. Fuzzy set theory is incorporated to improve the interpretability or perception of information in the images. It handles uncertainties (arising from deficiencies of information available from situation like the darkness which results from incomplete, imprecise, and not fully reliable or vague features).

The fuzzy logic provides a mathematical frame work for representation and processing of expert knowledge. The concept of if-then rules plays a role in approximation of the variables likes cross over point. This is so because the uncertainties within image processing tasks are not always due to randomness but often due to vagueness and ambiguity. A fuzzy technique enables us to manage these problems effectively. Fuzzy inference system is the process of formulating the mapping from a given input to an output using fuzzy logic. The process of fuzzy inference involves processes which includes Membership Functions, Logical Operations, and If-Then Rules. The proposed technique used fuzzy if -then rules as a sophisticated bridge between human knowledge on the one side and the numerical framework of the computers on the other side, in a simple and easy to understand way.

The rest of the paper is divided into four sections. In the following section, we show the literatures reviewed and related works; this is followed by the section describing the methodology. Next we present the experiments conducted and the results obtained and finally, the last section contains our conclusion.

• II.    Related Works

Human beings have the ability to take in and evaluate all sorts of information from the physical world they are in contact with and to mentally analyze, average and summarize all this input data into an optimum course of action. Much of the information we take in, such as such as evaluation of the behaviour of a vehicle entering from a side street and the likelihood of the vehicle pulling in one’s front are not very precisely defined. We call this fuzzy input. In order to overcome the deficiencies of ordinary histogram equalization, reference [6], [7] and [8] proposed the adoption of plateau histogram algorithm in which plateau threshold is set to a fixed value to suppress image background and then both gray density and gray interval of histogram are equalized to enhance image. However, many gray levels are still united together and target and details are often lost, thus making the image to become dimmer. These changes usually constitute the high frequency part of the image. So, one way for image contrast enhancement is to enhance or amplify the amplitudes of these high frequency features. UnSharp masking [10] is a simple Laplacian based contrast enhancement technique in this way. In [9], doubleplateaus histogram enhancement algorithm is proposed. Guliato D et al in [12], adaptive fuzzy histogram equalization was studied; this is an advanced version of ordinary histogram equalization but works by segregating images into sub-images before equalization which makes it computationally intensive. Also fuzzy wavelet and contour based contrast enhancement was studied in [13], they applied the method to both separable and non-separable transforms, they claimed to get a good result with their algorithm.

• III.    Methodology

The following section discusses the idea in which our system is based upon. We looked at fuzzy logic and fuzzy set concept and the fuzzy histogram equalization amidst other things, we stylishly present underlying concept of the proposed system and how it’s been implemented. The following sub-sections describe the system in detail.

• A.    Fuzzy Logic

  Fuzzy Logic is built on The Fuzzy Set Theory. The invention, or proposition, of Fuzzy Sets was motivated by the need to capture and represent the real world with its fuzzy data due to uncertainty. Uncertainty can be caused by imprecision in measurement due to imprecision of tools or other factors. Uncertainty can also be caused by vagueness in the language. We use linguistic variables often to describe, and maybe classify, physical objects and situations. Fuzzy logic is a technique that attempts to systematically and mathematically emulate human reasoning and decisionmaking. Fuzzy logic allows scientists to exploit their empirical knowledge and heuristics represented in the “if/then” rules and transfer it to a function block. The concept of fuzzy sets was introduced by Prof. Lofti Zadeh in 1965 [18]. Since then, the theory has been developed by many researchers and application engineers. In classical set theory, a set is defined by a characteristic (membership) function that assigns each element a degree of membership: either 0 (the element

is not member of the set) or 1 (the element is member of the set).

Fuzzy set theory is the extension of conventional set theory. It handles the concept of partial truth (truth values between 1 (completely true) and 0 (completely false)). A pictorial object is a fuzzy set which is specified by some membership function defined on all picture points. From this point of view, each image point participates in many memberships. Some of this uncertainty is due to degradation, but some of it is inherent. In fuzzy set terminology, making ground distinctions is equivalent to transforming from membership functions to characteristic functions.

• B.    Fuzzy Set Definition

Fuzzy sets generalize classical (crisp) sets and the degree of membership to a fuzzy set can take any value in the real unit interval [0, 1]. More formally, a fuzzy set A is defined by its membership function A: X->[0,1], where X is a domain of elements (universe of discourse). For every particular value of a variable x ∈ X the degree of membership to fuzzy set A is A(x). The variable x is called the linguistic variable and corresponding fuzzy sets defined on the range are called linguistic terms described by name (label) and membership function.

For a finite set A= {x1,..., xn}, the fuzzy set ( A, m) is often denoted by {m( x1) / x1,...,m(xn) / xn}.

Let x=1, then x is called not included in the fuzzy set (A, m) if m(x) = 0, x is called fully included if m( x) = 1, and x is called fuzzy member if 0 < m(x) < 1.

The set { x A|m(x)>0}is called the support of ( A, m) and the set{ xA|m(x)=1} is called its kernel.

The idea of fuzzy sets is simple and natural. For instance, we want to define a set of gray levels that share the property dark. In classical set theory, we have to determine a threshold, say the gray level 100. All gray levels between 0 and 100 are element of this set; the others do not belong to the set. But the darkness is a matter of degree. So, a fuzzy set can model this property much better. To define this set, we also need two thresholds, for instance, gray levels 50 and 150. All gray levels that are less than 50 are the full member of the set, all gray levels that are greater than 150 are not the member of the set. The gray levels between 50 and 150, however, have a partial membership in the set.

Fuzzy image processing is the collection of all approaches that understand, represent and process the images, their segments and features as fuzzy sets. The representation and processing depend on the selected fuzzy technique and on the problem to be solved.

Fuzzy histogram equalization is based on gray level mapping into a fuzzy plane, using a membership transformation function. The aim is to generate an image of higher contrast than the original image by giving a larger weight to the gray levels that are closer to the mean gray level of the image than to those that are farther from the mean. An image I of size M x N and L gray levels can be considered as an array of fuzzy singletons, each having a value of membership denoting its degree of brightness relative to some brightness levels. If we interpret the image features as linguistic variables, then we can use fuzzy if-then rules to segment the image into different regions.

Some simple fuzzy rules might be:

• 1)    IF the pixel is dark AND Its neighbourhood is also dark AND homogeneous THEN it belongs to the background.

• 2)    IF the pixel is not dark AND Its neighbourhood is also not dark AND homogeneous THEN it take it as the foreground

• 3)    IF the pixel is dark AND Its neighbourhood is bright AND homogeneous THEN redistribute the brightness thresholds

Fuzzy inference is the process of formulating the mapping from a given input to an output using fuzzy logic. The mapping then provides a basis from which decisions can be made, or patterns discerned. The process of fuzzy inference involves all of the pieces that are: Membership Functions, Logical Operations, and If-Then Rules. Three main processes are involved which are image fuzzification, modification of membership values and image defuzzification as shown in the figure below.

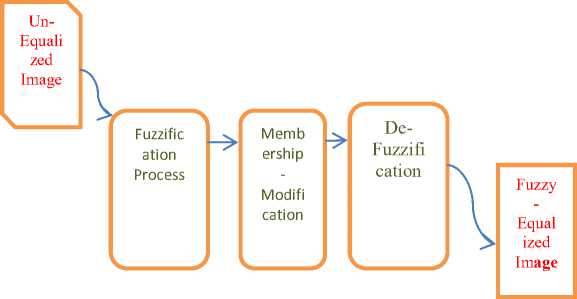
Fig.1 The FuzzificationProcesses

The mainstay of fuzzy image processing is the modification of membership values. After the image data are transformed from gray-level plane to the membership plane (fuzzification), appropriate fuzzy techniques modify the membership values. This can be a fuzzy clustering, a fuzzy rule-based approach, and a fuzzy integration approach. Fuzzy filters provide promising result in image-processing tasks that cope with some drawbacks of classical filters. Fuzzy filter is capable of dealing with vague and uncertain information. However, sometimes it is required to recover a heavily noise corrupted image where a lot of uncertainties are present and in this case fuzzy set theory is very useful. Each pixel in the image is represented by a membership function and different types of fuzzy rules that considers the neighbourhood information or other information to eliminate. Filter removes the noise with blurry edges but fuzzy filters perform both the edge preservation and smoothening. Image and fuzzy set can be modelled in a similar way. Fuzzy set in a universe of X is associated with a membership degree. Similarly, in the normalized image where the image pixels ranging from {0, 1, 2,…. 255} are normalized by 255, the values obtained are in the interval [0 , 1]. Thus, it is a mapping from the image G to [0, 1]. In this way, the image is considered as a fuzzy set and thus filters are designed.

• C.    Fuzzy Histogram Equalization

One of the most common approaches to image enhancement is by utilizing the statistical distribution of their intensities. Therefore, to achieve accurate and random equalization, it is important that pre-processing minimizes the effects of changing the statistical distribution or changes it properly to a predefined probability distribution function (PDF). Fuzzy Histogram Equalization is used to alleviate the effects of edge ringing on the histogram. This is done by using a weighted neighbourhood function when computing the histogram. This means that it builds a histogram for each pixel in the image, using a specified number of surrounding pixels. The breakdown of our algorithm is as given below:

We used fuzzy function proposed in [11] within a new form to provide a non-linear adjustment to the image based on the image gray level statistics. It attributes a membership value between 0 and 1 to the pixels based on the difference of their gray levels than a seed point, located in the image. The fuzzy function defined as:

F(p) = (Eqn 1) t+^d 1 ’

Where:

p is the intensity of the pixel being processed d is the intensity difference between p and a seed point and also

β controls the opening of the function.

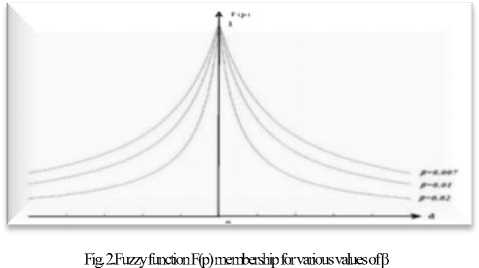
The larger the difference, the lower the membership function (F(p)); and as β increases, the opening of F(p) decreases. Fig. 1 visualizes the behaviour of this function.

The fuzzy histogram equalization being proposed is described as:

• ¹    (x,y) = A r (x,y) + { I (x,y) - A r (x,y)} F{|I(x,y) - A r (x,y)|}      (Eqn 2)

Where Ar (x,y) denotes the average of the gray levels of the pixels placed radially in distance r = V(x - xseed)2 + (У ~ yseed)2

away from a seed point, with radial distance (r) of 110 and A r = 121. The seed point is selected intuitively as a point in the image concern, i.e. the brightest region in the given image.. F(d) is the fuzzy function defined in equation 1.

I (x,y) is the original intensity of a pixel located at the coordinate (x,y). ' (x,y) is the new intensity of the same pixel in the processed image.

In equation 2 above, it is assumed that the intensities of the pixels at a radial distance (r) away from the seed point are similar unless there are in-homogeneities in the background. This assumption comes from the fact that masses in digital images appear as brighter areas that gradually darken from the seed point outwards toward the background, resembling an intensity variations profile similar to the presumed fuzzy function in as shown in fig.2 above and d indicates the radial distance from the seed point. Wherever there is a bright region in the background (due to background inhomogeneities), I (x,y) will be more different than Ar, i.e.

I (x,y) - Ar (x, y) = ∆ Lr (x , y ) will give a higher value.

According to equation 1 given above, F(∆ L r (x , y ) ) , will therefore yield a lower value. This, in turn, will attenuate the second term in the right hand side of equation 2, and ‘ (x,y) will be assigned A r . If there are no in-homogeneities in the background, then A r will be close to I(x,y), i.e. ∆ L r (x , y ) ≈ 0 and F(0) will yield unity, which in turn assigns ' (x, y) to I (x, y) (i.e. the intensity of the pixel does not change). In fact, equation (2) removes in-homogeneities or the small regions with a high contrast in the background. In addition, the proposed equation keeps the brightness and the contrast of the seed point. As a result, the proposed algorithm provides a smoothed image that is efficiently equalized and has a close agreement with the nature of the original image being processed. The function works similarly to ordinary histogram equalization albeit with a better result.

The fig.3 below shows the application of the fuzzy histogram equalization algorithm on some images of a particular subject from the database. For each row of images, the original image is followed by ordinary histogram equalized version of the image and lastly the fuzzy histogram equalized version of the image. It can be seen from below that where the background of the original image is very dark in some cases and the subject can rarely be seen, the ordinary histogram equalized version seems to be considerably clear albeit with clearly shown distortions and heavily pronounced noise in the images, also, the distinction between the fuzzy equalized version and ordinary equalized version can be clearly seen. The fuzzy equalized version seems to distribute the contrast and brightness evenly and clearly lightens up the face which is our major concern in the face recognition system. Also, where the original image is too exposed to light (as in row 2) and the ordinary equalized version tends to over-darken the image, the fuzzy version shows to get a perfect mix of the contrast and darkness by accurately darkening where needs to be darken and given perfect brightness where needed. It should be noted that in all the rows, the face of subjects in images normalized by fuzzy histogram equalization can be clearly seen; this is irrespective of the over-exposure or under-exposure of such images to light. This obviously makes the proposed method a good one for face recognition system in which we are mostly concerned about the subject’s face. Tables 1 to 3 show that recognition rate can be significantly improved with the application of this fuzzy equalization.

(Original)           (Ordinary equal)     (Fuzzy equalization)

Fig3. Images showing effects of equalization

• IV.    Experiments Conducted

A method of extracting features in a holistic system is by applying statistical methods such as Principal Component Analysis (PCA) to the whole image. PCA can also be applied to a face image locally; in that case the approach is not holistic. Irrespective of the methods being used, the main idea is the dimensionality reduction. A method usually used is the Eigenface Method by Turk and Pentland [15] which is based on the Karhunen-Loeve expansion. Their work is motivated by the ground breaking work of Sirovich and Kirby [16], [17] and is based on the application of Principal Component Analysis to the human faces.

The main idea here is the dimensionality reduction [14], [19], [20] based on extracting the desired number of principal components of the multi-dimensional data where the first principal component is the linear combination of the original dimensions that has the maximum variance; the nth principal component is the linear combination with the highest variance, subject to being orthogonal to the n-1 first principal components. The sole aim here is to extract the relevant information of a face and also capture the variation in a collection of face images and encode it efficiently in order for us to be able to compare it with other similarly encoded faces. The face recognition system used in this work is based on PCA algorithm stated above as implemented in [15]

This section presents the experiments conducted to ascertain the efficacy of the proposed algorithm in making the PCA based face recognition system robust to light variation. The experiments conducted are in three phases to show the discrepancy in results obtained for the recognition rate on our face recognition system when the images were normalized using ordinary histogram equalization and with the proposed algorithm, fuzzy histogram equalization. The system was trained with a database of 250 subjects each having 10 images in the database under different light intensity, scale and head orientations. The testing was carried out with 5 images each as test/probe images per subject. The test cases were constructed differently to measure the accuracy level of our system under the following conditions:

• •    Ordinary Histogram equalization is performed on database members for illumination independence

• •    Fuzzy Histogram equalization is performed on database members    for illumination

independence

• •    No Histogram equalization is performed

• V.    Experiments Conducted

We present the results obtained for the recognition rate on our face recognition system when ordinary histogram equalization is used and the proposed fuzzy histogram equalization is used. We applied a rescaling algorithm for all the images to be of the same scale, background removal was not done to mimic a real scene experience but manual cropping was made where needed on the database members. The algorithms were implemented successfully using MATLAB and trained and simulated on a Pentium-IV (2.4 GHz), 2GB RAM to provide valuable results. The tables below shows the summary of the results obtained.

Table1. Table showing the recognition rate when all images are fuzzy histogram equalized

Total Number of Images	Total no of subjects	Number of training images per subject	Number of test images per subject	Average recognition rate (success)
2500	250	10	5	96.7%
2500	250	7	5	94.9%
2500	250	5	5	90.3%

Table2. Table showing the recognition rate when all images are ordinary histogram equalized.

Total Number of Images	Total no of subjects	Number of training images per subject	Number of test images per subject	Average recognition rate (success)
2500	250	10	5	89.7%
2500	250	7	5	85.9%
2500	250	5	5	79.8%

Table3. Table showing the success rate when images are not equalized

Total Number of Images	Total no of subjects	Number of training images per subject	Number of test images per subject	Average recognition rate (success)
2500	250	10	5	78.8%
2500	250	7	5	70.2%
2500	250	5	5	62%

• VI.    Conclusion

This work presents an illumination invariant face recognition system. The result was achieved by applying fuzzy histogram equalization as against ordinary histogram equalization to achieve illumination invariance. The result obtained has shown that the proposed fuzzy histogram equalization increases the recognition rate of the system significantly. Further works can include the application of other filters with the fuzzy filters to achieve better result.

Acknowledgment

The authors acknowledge the help of senior faculty members of the department of computer science, university of Ibadan, Nigeria and other anonymous reviewers to whom we are forever grateful for their careful reading of this paper, constructive criticism and helpful comments.