Energy-efficient and Load Distributed Clustering Algorithm for Dense Wireless Sensor Networks

Published Online May 2017 in MECS

WSNs are a collection of a huge number of sensors, deployed in the area of interest to observe environmental phenomena. Their basic operations are to detect events, generate event-based data and transmit it to the base station. Sensors are battery equipped and mostly deployed in hostile environments [1]. As sensors are tiny in size, equipping them with high power batteries is difficult and cost effective. Due to the massive number of nodes and environmental conditions, replacing power outage nodes or recharging their batteries is highly complicated or infeasible [2] [3]. So, the lifetime of the network highly depends on energy utilization of a sensor in the network. Therefore, reducing the energy consumption of sensors is a major objective in the design of WSNs. Primary energy consuming operations in sensors are data reception, data processing, and data transmission. Of the three data transmission is identified as a major energy consumer [4], [5], since energy consumption rate of transmission is directly proportional to the communication distance.

As data transmission consumes more energy, an energy efficient routing is a prominent solution to reduce the sensors energy consumption. Among many routing techniques, energy aware clustering is most preferred and offers on excellent hierarchical data collection mechanism. In clustering, nodes are grouped into clusters and, from each cluster one special node is chosen as clusterhead (CH), which is responsible for inter and intracluster data management. CHs collect data packets from cluster members, aggregate them into a single packet and forward it to the base station. Data aggregation of CHs reduces the network’s transmission rate and avoids data redundancy.

Due to high data processing overheads, premature death of CHs is a major issue in the design of clustering algorithms [6]. To overcome this, existing algorithms perform periodic re-clustering, but every attempt of reclustering generates more control messages. Hence, nodes spend additional energy to handle the control message overheads, which reduces the lifetime of the network drastically. During re-clustering, node’s data transmission is suspended, which is a major issue during time critical applications. To avoid CH’s premature death and the suspension of data transmission, the proposed ELDCA algorithm provides a novel, independent, local CH substitution mechanism for CH’s suffering from energy issues. Also, ELDCA distributes nodes among clusters by allowing them to choose their CH through a defined cluster fitness value.

The rest of the paper is organized as follows: Section II describes the relevant clustering algorithms. The network and radio model of the proposed algorithm is discussed in section III. Section IV describes the proposed algorithm ELDCA. The performance evaluation of the proposed algorithm is presented in Section V. Finally, Section VI concludes the paper.

• II.    Related work

This section discusses some important clustering methods relevant to the proposed algorithm. With regard to construction methods, clustering algorithms are classified into three types: random clustering, tree-based clustering, and pre-structured clustering. In the random clustering method, CHs are chosen randomly across a network and other adjacent nodes join the nearest CH that form a cluster. In LEACH [7], CHs are randomly chosen through a distributed algorithm with a node probability p . All the other nodes independently choose their CH, having a minimum communication distance. The distribution of energy consumption among nodes is achieved by the periodical rotation of CHs and through data aggregation. LEACH follows single hop communications for data transmission. So, nodes need to transmit data to longer distances to reach a CH. Due to random clustering, LEACH suffered from uneven cluster sizes and the higher probability of two neighbouring nodes becoming CH. Another familiar random clustering protocol, HEED proposed in [8], unlike LEACH, used residual energy as primary criteria to select CH and nodes join with higher degree CHs. It also allows multi-path inter-cluster communication. Here the probability of two neighbouring nodes to become CH is very small but still, the clusters suffer from uneven load distribution.

In tree-based clustering, nodes are formed like a tree and each non-leaf node in the tree acts as a CH. Most tree-based clustering algorithms were constructed by solving a well-known mathematical problem called connected dominating sets (CDS) [9] [10] [11] [12]. Initially, these algorithms were constructed CDS under specific conditions; later nodes in CDS formed clusters using neighbouring nodes. In 1998, Guha et al., proposed two centralized greedy heuristic algorithms [6] for dominating set problem. The first algorithm was a growing tree (T) based algorithm, starting from a maximum degree vertex as a root. In each step, one more fitted-vertex is added to T. The second algorithm has two phases, the first phase grows separate block of connected components to form a dominating set. The second phase uses the Steiner tree algorithm, which connects a pair of connected components by a chain of vertices. Wightman, Pedro et al. proposed a growing tree-based topology construction protocol (A3) [10], which offered a sub-optimal CDS for data collection and it turns off the unnecessary node while network connected and covered. Active nodes selected based on the distance from the parent and remaining energy of the node. As A3 select the farthest node as an active node, it suffered by longer distance communication. A centralized cluster based energy-saving routing architecture (ECRA) proposed in [13], constructs clusters using the modified k-means clustering algorithm to maintain ideal cluster distribution. It has two phases: setup and steady state phase. In the setup phase, the network was clustered using k-means clustering approach and a node which nearer to every mean point of the cluster was selected as a CH. Further, multi-hop tree constructed for intra-cluster communication with defined hop count. Steady state phase performs data collection using TDMA schedule.

In pre-structured clustering algorithms, the network region is virtually divided into specific, identical shapes with each shape representing a cluster. Shapes may be concentric circles [14], [15] or grid cells [16], [17], [18] or particular subareas. Among the above-mentioned clustering methods, the grid-based clustering method is preferred due to its efficiency and simplicity [19], [20], [21]. In this method, the network region is divided into number of grid cells with each being treated as a cluster. Determining grid cell size is a major issue in grid-based clustering. When the grid size is small, a grid may have less number of nodes and in some extreme cases not even a single node. If it is too large, communication between CHs is suspicious to succeed. In [18], a grid-based clustering algorithm was proposed and analysed with three grid cell sizes. The values of grid size (S) were used as S = 2 r / 10 , S = rJ 2/3 and S = r /2 J 2 , where r was the maximum transmission range of the nodes. Among these three values, GRID performed well, when grid size was S = rsi 2 /3 . In [17], to cover the side and diagonal neighbouring grids, grid size was defined as S = r /V5 . Some recent grid-based clustering algorithms used smaller grid sizes [16], [22], to maximize the number of neighbouring CHs to ensure efficient route construction.

In 2005 TTDD [19] provided a two-tier data dissemination routing algorithm (i.e., high and low) with multiple mobile sinks. Grids were built on a source basis, so the number of grids depends on the number of sources. Source node proactively builds the grid structure to cover the entire network. Further, it forwards data through intermediate nodes, which are closer to the grid crossing points. These intermediate nodes are called dissemination nodes. The dynamic, per-source grid construction method of TTDD is suffered by higher grid construction overheads, specifically, when the number of the source increases. Further TTDD improved in GMDQP [23] by reducing overhead grid construction costs, where the grid was constructed from the sink side and not from the source node.

An energy-aware grid-based routing scheme (EAGER) proposed in [18], constructed grids with size S = r/2V2, and used multiple mobile sinks for efficient data dissemination. According to the allotted sleeping period, idle CH was allowed to switch off its radios periodically. Due to multiple mobile sinks, data is transmitted over unstable and long routing paths, which increases the energy cost of delivering data. To overcome this, EAGER performed re-routing. In [16], a grid based fault tolerant clustering and routing algorithm (GFTCRA) was proposed to address the hot spot problem and fault management in WSNs. The size of the grid was defined as S = r/2.85 , which ensured that any CH is adjacent to fifteen other CHs and also it has a maximum of seven distinct paths to reach the sink. Among all available distinct paths, GFTCRA chose the shortest path called primary path to send data from CH to sink. When any intermediate CH on the primary path failed, the sender chooses the next shortest path as a primary path. However, GFTCRA does not distribute normal nodes among clusters, leading to uneven energy consumption in CHs, resulting in the early energy drain of CHs. This paper is intended to construct stable and balanced clusters. Hence, we define a cluster fitness value to balance the clusters. Cluster fitness value is calculated based on the distance of nodes, network density and the node’s residual energy. To attain cluster stability, we adopt a local substitution mechanism to replace energy deficient CHs. This substitution mechanism avoids CHs premature death and reduces control message overheads through reclustering.

• III.    Network and Energy model

This section described the network and energy model of the proposed algorithm. The network model is discussed in subsection III-A and energy model is represented in subsection III-B.

• A.    Network model

The proposed network model adopts some of the following assumptions: The  ‘n’ number of energy constrained homogeneous sensor nodes are deployed in a two-dimensional area of interest (L x L ) with compatible density for guaranteed coverage and connectivity. Nodes transmission and sensing ranges are equal. After deployment, sensor nodes are stationary and unattended. The base station or data collector is located at the centre of the deployment region with the unlimited power source. Nodes are equipped with a unique battery source and the same amount of energy (in joule) at the time of installation. Transmission range (r) of a node is adjustable. When any two nodes are neighbors, they must reside within the transmission range (r) of each other. The nodes are unaware of their location information but can find the approximate distance of neighbours using Received Signal Strength Indicator (RSSI) [23].

• B.    Energy model

The proposed work follows the first order radio model described in [13],[16]. So, the radio transmitter and receiver circuitry energy consumption E     is set as

50 nJ/bit , transmitter amplifier dissipate is set to 10 pJ / bit / m ² for free space propagation model ( e ) and 0.013 pJ / bit / m ⁴ for the two-ray ground model ( s ) (multipath). Energy consumption to transmit l bit message over distance r is calculated as

E T ( l , m ) =<

if Г <  1

ifr >  1

and the energy consumption to receive this message is

Er ( l ) = l X E eie _C              (2)

• IV.    Proposed algorithm (eldca)

This section describes the clustering process of the proposed algorithm. Grid construction process is illustrated in subsection IV-A. Subsection VI-B describes the setup phase and pseudo code of the proposed algorithm. The steady-state phase of ELDCA is presented in subsections III-C.

• A.    Grid Construction Process

Initially, the network region is divided into many virtual congruent square grids. When any two grid cells are neighbouring cells, they must share a common cell border or a common corner. So, a grid cell may have a maximum of eight neighbouring cells. In grid-based clustering, defining the size of the grid cell (denoted as S ) is a major issue, [10]. If S is small, the grid cell has limited nodes in it, and in extreme cases; a node in the network will be a CH in its own grid that avoids the benefit of clustering. When S is too large, communication between the CHs become suspicious. So, more attention is needed to formulate the value of S . To provide the local substitution for energy suffering CHs, the proposed algorithm prefers a specific circular region at each inner grid crossing point (the corner common to four grid cells), called clusterhead region (R). Nodes from this region R are reserved for selection of CH and they act as a CH when their turn comes. To attain the enhanced lifetime for WSNs, the region R should assure the availability of certain percentage of nodes in it. Therefore, the proposed algorithm considers network density and nodes transmission range to define the region R. To assure inter-cluster communication, the maximum distance between any two nodes in the adjacent R regions should be less than or equal to r . Fig.1 illustrates the estimation of grid cell size. Circles with diameter d represent R region. The dark square represents area (A) of the proposed grid cell. Let S be a size of a grid cell, defined as

S =

r - d

where r refers transmission range of nodes. Fig.2, shows the block diagram of the proposed grid structure with 6 X 6 cells. In this, the shaded circles represent clusterhead region R and is identified using a sequence of numbers (denoted by ID ( R ) ).

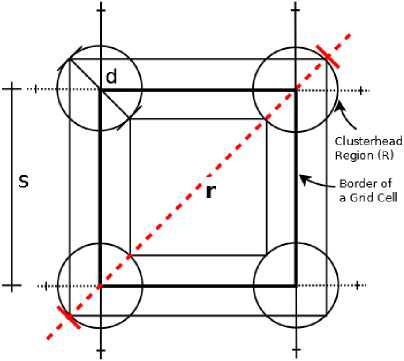
Fig.1. Grid size calculation

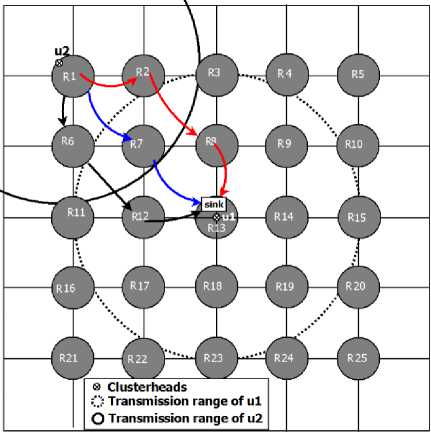
Fig.2. Black diagram of the proposed grid structure

In the proposed grid structure, CHs can directly communicate with eight other CHs in maximum and three in minimum, as shown in Fig.2. So, any CH has a possibility of three distinct paths to reach the sink in the worst case, which is represented by arrows between the R 1 to the sink. This grids construction is done by the proposed algorithm only once in the network’s lifetime.

• B.    Setup phase

This section describes the selection of CHs and the cluster formation of the proposed algorithms. During clustering the state of a node is categorized into two; covered and uncovered . If a node is a member of any cluster then its state is covered or else it is uncovered . Table 1 contains relevant notations used in this discussion. After grid construction, at each R , a node closer to O is chosen as the initial active CH. The initial CHs are responsible for cluster formation. Let u be the initial active CH of R , which broadcasts one special joining message ( J ) to N ( u ) . This message contains ID ( R ) , O i , M ( R i ), CS ( R i )and E avg ( R i ).

Table 1. Notations and abbrevations

S.No	Notations	abbreviations
1.	Ri	ith clusterhead region
2.	ID ( Ri )	Identification number of R
3.	N ( v )	Neighbors of node v
4.	Oi	The origin of R
5.	M ( Ri )	The number of nodes which belong to R
6.	d ( u , v )	Distance between node u and v
7.	CS ( Ri )	Expected cluster size of R , is calculated as CS ( R i ) = £ u { d ( u , O i ) <  ( S /2)}
8.	E r ( u )	Residual Energy of node u
9.	E avg ( R i )	Average residual energy of Ri, calculated E ( u ) as Eave ( Rj ) = ^-----, V u e R avg i      M ( R )           i
10.	F ( v , R i )	Cluster fitness value of R with respect to node v .

Once the neighbours of u receive J , they will send a response message ( R ) with its node ID. When the state of v is uncovered , it directly join the cluster of u (i.e. R ). If it is already covered by another cluster, say R j , then it will join the cluster of u (i.e. R ), when F ( v , R_i ) is greater than F ( v , R ) or simply ignore J of u . F ( v , R )is a cluster fitness value of R_i with respect to v , it is defined as

F(v, R ) = ^a    x в E„_g (Ri) x ^Y C^S(Ri)    (4)

i    d(v,Oi)        avg i    M(Ri)

where ^a , P and У are balancing factors. In equation (4), the first two factors d ( v , R_i ) and E_avg ( R_i ) encourage the nodes to join the higher energy cluster with minimum distance and the third factor ^{CS ( Ri )} is used to balance the M ( R i )

load among clusters. After reception of R from the neighbours, u will finalize its cluster members. If v decides to join the cluster R then it is relieved from cluster R . The formal clustering network structure by the proposed algorithm is shown in Fig.3. Here, 2500 nodes are deployed in the area of 200 m x 200 m and node’s transmission range r is fixed as 70 m . In Fig.3, at the four grid crossing points, a total of sixteen clusters are constructed. Let K be the number of rows (or column) in the constructed grid structure. Then the number of clusters is ( K - 1)2 . The pseudo code of the proposed algorithm is presented in algorithm1.

• C.    Routing Phase

During the routing phase, nodes transmit sensed data to the sink. Once clusters are constructed, the TDMA schedule is determined for data transmission. All cluster members send the data directly to its CH in the scheduled time slot. The proposed algorithm uses the global addressing scheme for data collection. In this scheme, clusters are identified by through the respective region IDs (i.e. R ) rather than the node ID of an active CH. Once data packets are received from all cluster members, an active CH aggregates them into one packet and transmits it to the sink either directly or through intermediate CHs.

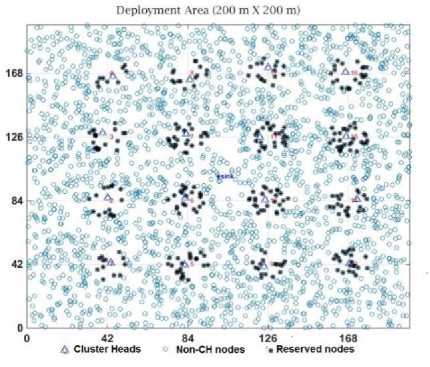
Fig.3. Proposed WSN grid structure

Algorithm 1 (ELDCA(G(V, G),r,L))

1. Find S =

r - d

2. Find K =

L

S

• 3.    Divide the deployment area L x L into

• 4.    Select R_i at each four grid crossing points

• 5.    Foreach R_i do

• 6.            Select u as CH_i , min( d ( u , O_i ))

• 7.           u send J msg to N ( u )

• 8.           For all v e N ( u ) do

• 9.             If State ( v ) ^ ' uncovered '

• 10.                v send R    to u

• 11.                Set head ( v ) ^ R i

• 12.              Else

• 13.                    ' do nothing '

• 14.             End If

• 15.         End For

• 16.    End For

K2 number of Grid cells

or (F(v, Ri) > F(v, Rj ))then v Rj is current cluster of v

msg

When the base station is not in r distance, CHs have chosen the higher energy path from the available distinct paths to send their data. Let N be the number of hops in path P , then energy of path P is defined as

E(P) =

E ^E avg (^R i )

N P

, V R i e P

A complete data transmission from all sensors to the sink is referred as a round. During routing period, if the residual energy of a current CH of R is reduced to a certain percentage from E ( R ), it will be replaced by a higher energy node from R . The current CH is merely responsible for selecting the replacing CH. Let u be the current CH of R and p a defined percentage of energy to substitute an active CH. Then u will be substituted if the following condition is satisfied,

E ( u ) res       ^p

E(R)  100, avg i

As u is responsible for selecting a new active CH, it broadcasts a control message with an intention to collect current energy status of nodes in R . From the received response messages of nodes in R , it chooses a higher energy node as a new active CH and u start acts as a normal node till its turn. The substitution procedure is presented in algorithm 2. The probability of a node in R to become a CH is1/ M ( R ) . As the proposed algorithm uses the global addressing scheme, cluster members need not update the CH substitution. Hence, the energy consumption of cluster members by control message overheads of CH substitution is totally avoided. Thus, this substitution based CH rotation significantly reduces nodes energy consumption and avoids CHs early depletion.

Algorithm 2  ( CLUSTER SUBSTITUTION )

E r ( u )

• 1.    Find E . ( R ) = ^-----, V u e R avg i      _{M ( Ri )}           i

• 2.    Set Th ( CH, ) = E ^{res (} CH ¹ ) x 100 ^{i      E}avg ^{( R}i ⁾

• 3. 7/ Th ( CH ) <  p

• 4.    Select v as new CH i , v e R i &&max( E r ( v ))

• 5.    Sent S to v msg

• 6.    End If

• D. Energy consumption Analysis of proposed algorithm per round.

Each sensor node generates l bits of data and send it to the corresponding CH at each round. Assume CH and n are the cluster head and the number of cluster members of R respectively. Hence from Equation (1), the energy consumption for sending data from all the cluster members to CHi is expressed as ni

E m ( R i ) = £ l * E elec + ¹ * ⁶ fs * ( d ( ^i’ ^UJ ^    (7)

j =1

Also form Equation (2), the energy consumption of CH for receiving data from cluster members is expressed as

E r _ec ( CH i ) = n ( 1 * E ),           (8)

E Collect ( R i ) = E c _m ( R i ) + E rec ( CH i) ,         (9)

Once data collected from entire cluster members, CH performs data aggregation. Let E_DA be the energy consumption to aggregate one bit of data. Then the energy consumption for data aggregation is given as

E agg ( CH i ) = ( n + 1)( 1 x E da ),           (10)

Since CH_i also performs sensing operation, data of CH is also included in the data aggregation. Let l be the aggregated data length of CH i and f e (0,1) is the data aggregation factor [24]. Then l_i is calculated as

, ₌ ^{1X (} n i + 1) '" ni f agg + 1’

Further, CH_i sends aggregated data to the base station through multi-hop model. The energy consumption due to multi-hop data forwarding is calculated as

N P

E m _ hop ( CH i ) = 1J £ 2 E elec + ( ^ mp X d ^ ),      (12)

j =1

Total energy consumption of proposed algorithm per round is calculated from equations (9), (10) and (12),

E perRound

( k - 1)²

= E [ ECollect(Ri) + Eagg (CHi) +Em_hop (CHi)], i =1

• V.    Results and Discussion

The performance of the proposed algorithm is evaluated with respect to network lifetime and node’s energy consumption rate. Extensive numerical simulations were conducted using MATLAB R2014b as a simulator to demonstrate the efficiency of the proposed algorithm. The results from the average of 100 experiments were compared to the existing clustering algorithms. Network lifetime is measured in terms of rounds. One round represents one complete data transmission from nodes to the sink. To show the superiority of the proposed algorithm, the comparison analysis was made with very well-known and dissimilar clustering techniques like GFTCRA (grid-based clustering), ECRA (k-means clustering), HEED and LEACH (random clustering). To ensure a unified comparison, the compared algorithms experiment under similar network setup and energy models. The parameters used in the experiments are given in table 2.

Table 2. Simulation Parameters and values

Network Size	500 to 2500
Deployment area	300 square meters
Base station/sink position	Middle of the Area of Interest
Data Packet size	2000 bits
Control packet size	100 bits
Energy Consumption for data Transmission and reception	50 nJ
Energy consumption in free space/air	0.01 pJoule
Initial node energy	1 Joule
Sensors Transmission Range	75m

As the proposed algorithm substitutes CHs, based on the value of p , defining p is significance to prolong the lifetime of the network. When p is maximum (i.e., 70%, 80%), CHs are substituted frequently. So, CHs spend more energy to handle control message overheads by the substitution process, which reduced their lifetime considerably. When p is minimum (i.e. 20%, 30%), CHs energy is drained totally when substituted, so that it lacks enough energy to perform the next CH chance. In worst cases, CHs die earlier than it second chance. So, to control substitution frequency and maintain CHs operational energy, p should be fixed at an optimal value. Hence, the proposed algorithm determines the value of p based on the experimental analysis. As regards, the lifetime of the network is evaluated under the substitution of CHs using various p values (i.e., 40%, 50%, 60%, 70%, and 80%), as shown in Fig. 4. As network lifetime is evaluated as rounds, it is calculated from the initialization of the routing phase to first node failure. The result from Fig. 4 reveals that the proposed algorithm yields higher lifetime when p is 60%. Therefore, the value of p is fixed at 60% for further experiments.

The network lifetime of the proposed and compared algorithms are analyzed under two categories of round estimations. In the first category, rounds are estimated till first node failure and the results are shown in Fig.5. In the second category, rounds estimation is extended up to 30 percentage of node’s failure, which is shown in Fig.6. A network with thousand nodes is considered for analysis.

The algorithm GFTCRA uses small grid size to build grid structure, which increases the number of grids considerably. As each grid cell acts as a cluster, the number of data transmissions increased. Also, GFTCRA does not perform load distribution among clusters or reclustering.

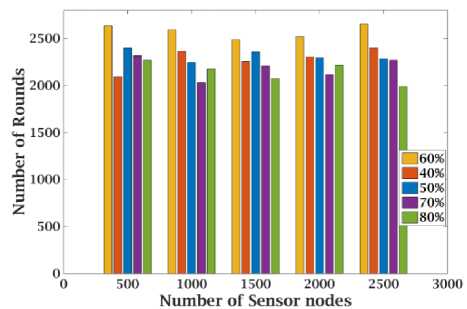
Fig.4. Lifetime of the networks for various p values.

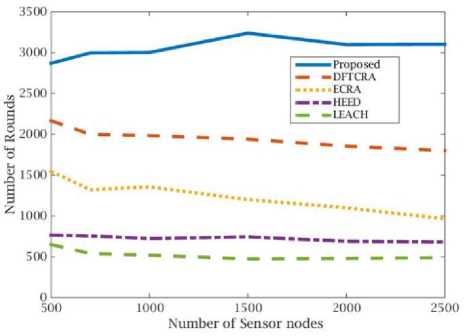
Fig.5. Comparison results of networks lifetime against various network sizes.

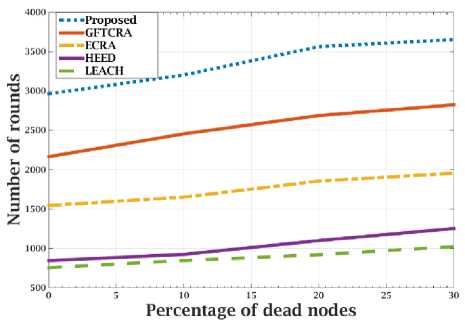
Fig.6. Comparison results of networks lifetime against various percentages of dead node s.

Due to this higher data transmission and uneven cluster formation of GFTCRA, CHs energy consumption increases extensively and as a result draining its energy early. Even fault management of the algorithm did not benefit to extend the lifetime of the network. In ECRA, clusters were constructed based on the K-means clustering approach. K-means clustering method does not consider clusters load balancing, and it forms clusters based on the distance between nodes and clusters mean points. As a result, CHs suffered due to uneven load dissemination and die quickly. ECRA also constructs a multi-level tree for intra-cluster communication, which makes nodes participate in data forwarding unnecessarily. Also, nodes spend more energy for re-constructing the multi-level tree while re-clustering. As HEED and LEACH algorithms randomly construct clusters, CHs suffered due to uneven node distribution. Nodes also need to transmit data over longer distances. As mentioned earlier, data transmission consumes more energy and is directly proportional to the distance between source and destination. So nodes spend more energy for successful transmissions.

Unlike the above-mentioned algorithms, the proposed algorithm reduces the uneven energy consumption of CHs by distributing nodes among clusters using a cluster fitness value. Due to this, nodes join the nearest optimal cluster and considerably reducing their energy consumption. The proposed ELDCA avoids CHs early energy depletion by providing the local substitution for energy suffering CHs. As it follows the global addressing scheme for data transmission, transmission overloads through re-clustering are also avoided totally. Therefore, the lifetime of the network is drastically increased by the proposed algorithm compared to other algorithms, as verified in figures 5 and 6. The results show that the proposed algorithm increased the network lifetime of by 27% than GFTCRA, by 50% than ECRA, and by 200% compared to the LEACH and HEED algorithms.

To address nodes energy dissemination accurately, the average remaining energy of nodes need to be considered at the end of every simulation. The average remaining energy of nodes is calculated at the end of each experiment and the average of the obtained results is considered for analysis. Fig.7, represents the average remaining of reserved (nodes in R ) and normal nodes (cluster members) by the proposed algorithm for various network sizes. In this, the difference between two curves shows that the proposed algorithm disseminates the energy consumption of nodes excellently. Also, nodes energy dissipation rate is almost equal for all network sizes, revealing that the proposed algorithm is highly reliable for dense WSNs.

The comparison between the algorithms in terms of nodes energy utilization against various network sizes and experiments are terminated at first node failure. Fig. 8 shows the average remaining energy of nodes against network lifetime in comparison with other algorithms. As the compared algorithms use unique energy model, energy consumption rate of the network is inversely proportional to the network lifetime. Hence, energy balancing algorithms must utilize more network energy and prolong the network lifetime accordingly.

0.9

Normal Nodes

R nodes

Ui

£

0.8

0.7

я

0.6

s

0.5

0.4

0.3

Network Size

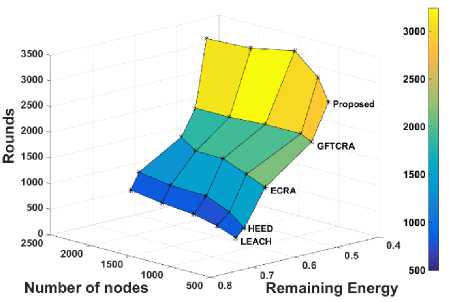
Fig.8. Comparison results of residual energy of nodes.

Fig.7. Analysis of energy dissemination

Due to re-clustering overloads and uneven nodes dissemination of clusters, the other compared algorithms suffered from CHs premature death. Hence, network lifetime of the compared algorithms ends earlier even with nodes having more residual energy, showing their poor resource and energy utilization. But, the proposed algorithm effectively distributes nodes among clusters using a cluster fitness value and also completely avoids re-clustering overheads. So, nodes energy is used efficiently by the proposed algorithm, thereby improving the lifetime of the network, which is shown in Fig.8. In Fig.9, the comparison results of nodes average remaining energy against various percentages of dead nodes is shown. In this, almost 75% of the network energy utilized by the proposed algorithm before 30% of nodes death. This proves the superiority of the proposed algorithm in overall energy utilization of nodes.

• VI.    Conclusions

This paper presents an Energy-efficient and Load Distributed Clustering Algorithm for dense wireless sensor networks (ELDCA), built with an intent to increase energy efficiency and balances the node energy utilization. Nodes are evenly distributed among clusters using a cluster fitness value based cluster selection method. As the premature death of CH is a major limitation in the design of clustering algorithms, the proposed algorithm employ independent cluster substitution for energy deficient CHs. Also, avoids additional energy consumption of cluster members due to control message overheads in CH substitution process. Simulation results in diverse network scenario have shown that the proposed algorithm ELDCA significantly prolongs network lifetime and efficiently distributes the node’s energy consumption than current algorithms DFTCRA, ECRA, LEACH and HEED. Also, ELDCA employs almost 75% of the network energy before 30% of nodes death.

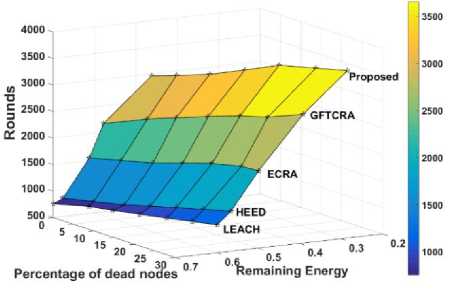
Fig.9. Comparison results of nodes remaining energy against various percentages of dead nodes.

Acknowlegdement

This research has been supported and funded by the Ministry of Human Resource Development (MHRD) under the government of India.