Enhanced Hopfield Network for Pattern Satisfiability Optimization

Published Online November 2016 in MECS

Satisfiability problem is a paradigmatic constraintsatisfaction conundrum with zillions of applications, such as in pattern reconstruction and circuit configuration [1, 16]. Traditionally, the pattern reconstruction deals with the geometrical field and implemented the conventional technique to verify the pattern via neural network [8, 14]. Technically, we proposed a paradigm to verify the pattern and recall it back after certain training process. So, we combine the benefits of 3-Satisfiability, Logic Programming, Hopfield Neural Network and activation function to verify the pattern satisfiability problem. The

Pattern Satisfiability problem (Pattern-SAT) is a brand new conundrum that inspires researchers to create model verification techniques which help in generating correct pattern. For many practical reasons, it is becoming very difficult to manually recall the stored pattern because it will end up with a large number of fault. Hence, the generated pattern will be disturbed by monstrous amount of noises.

In order to minimize the problem, Hopfield neural network is the perfect network due to the existence of remarkable content addressable memory (CAM) [2, 3]. Hence, recurrent neural network are essentially dynamical systems that feedback signals to themselves [6]. Then, the Hopfield neural network is a simple recurrent network which can work as an efficient associative memory, and it can store certain memories in a manner rather analogous to the brain [3, 11]. In addition, it is a branch of neural network that assist the researchers in constructing the model of our brain. Thus, it is very practical to verify the pattern satisfiability problem. Hopfield neural network minimizes Lyapunov energy due to physical spin of the neuron states [15, 27]. The network produced optimal output by minimizing the network energy. Gadi Pinkas [9] and Wan Abdullah [4] defined a bi-directional mapping between logic and energy function of symmetric neural network. To frame their novelty, both methods are applicable to validate the solution obtained are models for a corresponding logic program. The work of Sathasivam [ 11, 28] showed that the optimized recurrent Hopfield network could be possibly used to do logic programming. Furthermore, intelligent technique of defining connection strength of the logic helps the network to overwhelm spurious state [15].

This paper has been organized as follows. Section I, formally introduces the important concept of Pattern Satisfiability, 3-Satisfiability, Hopfield neural network, logic programming and activation function. In section II, the important theory of 3-satisfiability (3-SAT) problems is discussed briefly. Then, section III covers the building block and algorithm for Pattern-SAT. Meanwhile, section IV presents the neuro-logic parts, including the fundamental concept of Hopfield neural network, logic programming and activation function used in our proposed network. In section V, theory implementation of the networks was discussed briefly. Finally, section VI and VII enclose the experimental results, discussion and conclusion.

• II.    S ATISFIABILITY (SAT) PROBLEM

Satisfiability problem is a well-known constraint-based problem in mathematics and computer sciences. Besides, the satisfiability problem has emerging as an optimization problem that can be solved by neural network. In this paper, we limit our analysis until 3-Satisfiability (3-SAT).

• A .    Boolean Satisfiability Problem

Boolean Satisfiability (SAT) can be demarcated as the decision problem since the solution will yield either “yes” or “no” response, by implementing the Boolean formula [12, 6]. Hence, SAT involves definitive task of searching truth assignments that satisfies a Boolean formula [7]. In other words, satisfiability problem refers to verdict problems based on particular constraints. In this paper, we emphasize 3-Satisfiability (3-SAT) to be embedded in Patter-Satisfiability (Pattern-SAT) problem.

• B.    3-Satisfiability Problem

In this paper, we emphasize a paradigmatic NP-complete problem namely 3-Satsifiability (3-SAT). Generally speaking, 3-SAT can be defined as a formula in conjunctive normal form where each clause is limited to at most or strictly three literals [21, 22]. The problem is an example of non-deterministic problem [12]. In our analysis, the following 3-SAT logic program which consists of 3 clauses and 3 literals will be used. For instance:

We represent the above 3 CNF (Conjunctive Normal Form) formula with P. Thus, the formula can be in any combination as the number of atoms can be varied except for the literals that are strictly equal to 3 [5, 24]. Hence, it is vital for combinatorial optimization problem. The higher number of literal in each clause will increase the possibilities or chances for a clause to be satisfied [11, 22].

The general formula of 3-SAT for conjunctive normal form (CNF):

P = a ; = z               (2)

So, the value of k denotes the number of satisfiability. In our case, k-SAT is 3-SAT.

Z = Ak=i(x,,y,,Zj),k > 3            (3)

• III.    P ATTERN S ATISFIABILITY

Pattern satisfiability is a brand new topic, combining the advantages of Boolean satisfiability concept and pattern reconstruction as a single optimization problem. Specifically, the pattern satisfiability (Pattern-SAT) requires a robust network to optimize the solutions. In this paper, the solutions refer to the ability to retrieve the correct pattern without noises.

• A.    Pattern Satisfiability (Pattern-SAT)

Pattern satisfiability is a mathematical model enthused by the means of Boolean circuit concept. In this paper, we will translate and construct the pattern according to 3-Satisfiability problem. The building block of our Pattern-SAT is depend on the particular 3-SAT formula. Strictly speaking, Pattern-SAT is a brand new combinatorial problem, where we need to consider the satisfied assignment in order to produce a correct pattern. We introduce the pattern satisfiability problem as Pattern-SAT. The most imminent fact is the pattern will be stored in Hopfield’s brain as a content addressable memory (CAM) [2, 14]. Hence, we combine the advantages of the Hopfield neural network and logic programming in pattern reconstruction according to 3-SAT. In our case, we proposed the 3-SAT Hopfield neural network to verify the correctness of the Pattern-SAT. Since, 3-SAT is NP problem, thus this conundrum can be verified within the polynomial time. So, Pattern-SAT can be concluded as NP problem. Note that Pattern-SAT has exactly 2 ⁿ consistent truth assignments before a pattern be activated, where n is the number of input points or the crucial points.

Modelling a correct pattern can be treated as combinatorial problem. We are required to construct the pattern according to the crucial points. First of all, we need to create a pattern according to the crucial points. We represent the crucial points of the pattern as the clause. Each crucial points, c are represented by 3

neurons. In order to produce the pattern, all the crucial points need to be activated. The more the crucial points, the more complex the system that we will train [5]. During the learning process, the constructed pattern will be checked before being stored to CAM. The concept similar to the Boolean circuit that requires all the component to activate before fully functioning [14, 17].

The satisfied pattern will be stored in content addressable memory (CAM) by distributing it among neurons [13]. After the relaxation process, we are going to recall the stored pattern the same way as biological brain works [26, 27]. Technically, the output is based on the correct pattern being recalled by our proposed hybrid network. Hence, in order to check the effectiveness of our proposed model in retrieving the pattern, we run the simulation until 100 trials. Hence, our proposed algorithm act as a robust brain model that can be implemented in other NP problem. The indicators are the number of correct retrieved pattern and time taken to recall all the patterns, given the 100 trials.

In our study, we will consider an alphabet pattern. We will increase the number of crucial points in order to check whether the retrieval power improve or not. For example, the pattern consist of the following crucial points IP = {c, c ₂, c } . In our study we will consider i = 5,10....50.

• B.    Implementation of Pattern-SAT

• 1)    Choose any pattern. For our case, we choose the alphabet pattern.

• 2)    Identify the crucial points in the pattern. We represent crucial points in the form of IP .

• 3)    Calculate the number of IP . Each crucial point represent by clauses c with 2 neurons.

P = C i               (4)

• 4)    Train c . We used ES, during learning. The network was trained 1000 iterations.

• 5)    Randomize the state of the neurons.

• 6)    The network relax based relaxation equation proposed by Sathasivam [27]

dh    dh dt      dt                  (5)

where h is the local field and R relaxation rate. The relaxation rate R reflects how fast the network relaxed. The value of R is an adjustable parameter and can be determined empirically.

• 7)    Retrieve IP by using Wan Abdullah Method [4].

• 8)    Construct the retrieved IP and check the correctness of the pattern (global pattern).

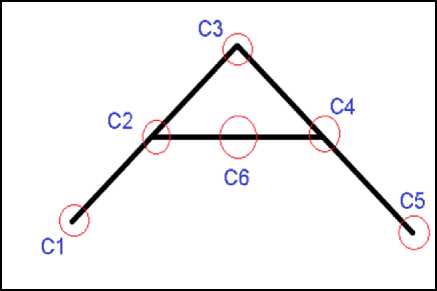
Fig.1. The alphabet used in Pattern-SAT with crucial points.

The above example contains 6 crucial points (circled in red). Each point represents the number of clauses added. Our aim is to ensure all the points are “activated” during retrieval phase. If the clause is satisfied, the points will be activated. The network also required to store the pattern in CAM. The network will be trained 1000 times.

• IV.    N EURO -L OGIC IN H OPFIELD N EURAL N ETWORK

Neuro-logic depicts the integration of Hopfield neural network and logic programming as a single hybrid network. In this paper, we enhanced the hybrid network by introducing the post optimization techniques, by using Hyperbolic Tangent activation function to solve Pattern satisfiability problem. In order to check the performance, we compared the proposed techniques with the conventional method, McCulloch-Pitts function.

• A.    Hopfield Model

In pattern satisfiability, we choose the Hopfield neural network because it is distributed and can be hybridized with the other algorithm [20,  21]. The pattern reconstruction is based on the crucial points and the ability to recall the stored pattern. Specifically, we opt to integrate 3-Satisfiability and the Hopfield neural network as HNN-3SAT in order to solve the pattern satisfiability (Pattern-SAT) problem [24, 25]. Basically, the Hopfield neural network is an ordinary model for content addressable memory (CAM). This structures emulates our biological brain whereby learning and retrieving data are the building block of content addressable memory (CAM) [2, 3]. The main concern is the ability of our proposed model to recall the correct pattern from the CAM.

In this paper, we will consider Discrete Hopfield Neural Network. Discrete Hopfield neural network is a class of recurrent auto-associative network [11, 15]. The units in Hopfield models are mostly binary threshold unit. Hence, the Hopfield nets will take a binary value such as 1 and -1.

The demarcation for unit I’s activation, a _i are given as follows:

J1 у V .      ^i ai = 1        j                                ( )

- 1 Otherwise

Where W_ij is the connection strength from unit j to i .

S j is the state of unit j and £ i is the threshold of unit i .

The connection in Hopfield net typically has no connection with itself W j = 0 and weight connections are symmetric or bidirectional.

Hopfield network work asynchronously with each neuron updating their state deterministically. The system consists of N formal neurons, each is described by an Ising variable. Neurons are bipolar S, e {1, —1} obeying the dynamics Sj ^ sgn(h) where the local field hi [6, 27]. The connection model can be generalized to include higher order connection. This modifies the field to h Y W2 Sj+ J1           (7)

The weight in Hopfield network is constantly symmetrical. The weight in Hopfield network refers to the connection strength between the neurons [4, 11]. The updating rule maintains as follows:

S i ( t + 1 ) = sgn [ h i ( t ) ]                     (8)

This property guarantee the energy will decrease monotonically even though following the activation system [24, 28]. Hence, it will drive the network to hunt for the minimum energy. The following equation represents energy for Hopfield network.

E = -■ — 1 ZY W" S i S j — Y W' S j      (9)

ij         i

• B.    Logic Programming in Hopfield Network

Logic programming is user writable, readable and be carried out in a neural network to obtain desired solutions.

Implementation of HNN-3SAT for Pattern-SAT in Logic Programming.

X = — (1 + S x ) and X = — (1 — S x ) . S x = 1 (True) and

S x = — 1 (False). Multiplication represents CNF and addition represents DNF.

• v.    Comparing the cost function with energy, E by obtaining the values of the connection strengths. (Sathasivam’s Method) [2, 27]

• vi.    Check clauses satisfaction by using exhaustive search. Hence, the satisfied clauses will be stored. In Pattern-SAT, the satisfied patterns will be stored as content addressable memory.

vii. The states of the neurons are randomized. The network undergoes sequences of network relaxation. Compute the corresponding local field h ( t ) of the state. If the final state is stable for 5 runs, we ponder it as final state.

viii. Find the corresponding final energy E of the final state by using Lypunov equation (9). Validate whether the final energy obtained is a global minimum energy or local minima. In Pattern-SAT, the final energy depicts the number of Global Pattern-SAT generated after each simulation. Next, the CPU time shows the performance of the proposed network to recall the correct pattern.

• C.    McCulloch-Pitts Function

The McCulloch-Pitts model of a neuron is modest yet has considerable computing prospective. The McCulloch-Pitts function is also having precise mathematical definition and easy to implement. Conversely, this model is very simplistic and tends to generate local minima outputs [11, 16]. Many researchers urged the alternatives for this function as it is very primitive and leads to slower convergence.

g( x ) = x                    ⁽¹⁰⁾

Another drawback is the linear activation function will only produce positive numbers over the whole real number. Thus, the output values are unbounded and not monotonic [3]. Hence, the outputs obtained will diverges from the global solutions.

• D.    Hyperbolic Tangent Activation Function

Hyperbolic tangent activation function is proven as the most commanding and robust activation function in neural network [11, 15]. Therefore, we want to explore whether the robustness of this function will apply to the 3-SAT logic programming in Pattern-SAT. Commonly, this function can be defined as the ratio between the hyperbolic sine and the cosine functions expanded as the ratio of half-difference and half-sum of two exponential functions in the points x and –x [10]. The Hyperbolic tangent activation function is written as follows:

. .               sinh( x )    e x — e ^— x

g ⁽ x ) = tanh⁽ x ) =--— = —---—        (11)

cosh( x )    e x + e x

The main feature of Hyperbolic tangent activation function is the broader output space than the linear activation function. The output range is -1 to 1, similar to the conventional sigmoid function [6, 10]. The scaled output or bounded properties will assist the network to produce good outputs. Hence, the outputs will converge to the global solutions.

• V.    I MPLEMENTATION

For implementation, we assigned any pattern for the network. The crucial points of the pattern will be determined. Each crucial points will generate random program 3-SAT clauses. From there, we initialized initial states for the neurons in the clauses. The network will evolve until final state reached. Once the program has reached the final state, the neuron state is updated via equation (7). As soon as the network relaxed to an equilibrium state, test the final state obtained for the relaxed neuron whether it is a stable state. Stable state will be considered provided the state remains unchanged for five runs. According to Pinkas [9], letting an ANN to evolve that lead to stable state where the energy function obtained does not change further. In this case, the corresponding final energy for the stable state will be calculated. If the difference between the final energy and the global minimum energy is within the given tolerance value, then consider the solution as global pattern.

• VI.    R ESULTS AND D ISCUSSION

  In this paper, Microsoft Visual C++ 2013 was used in simulating the results. In order to validate our proposed network, we carried out the simulations by using different number of crucial points. The main aspect in our analysis are the global Pattern-SAT and the CPU time for the enhanced network in pattern satisfiability optimization.

• A.    Global Pattern-SAT

To begin with, global Pattern-SAT is the percentage of correct pattern retrieved after 100 trials. The term ‘global’ here depicts the global solutions obtained in the form of correct pattern.

Table 1 elucidates the number of correct pattern retrieved after 100 trials for different number of crucial points. The capability to recall the correct pattern by implementing our proposed paradigm is the core impetus of our research. In this paper, we limit our number of crucial points to 50 as the training part consumes more time as we need to run until 100 trials. After that, we applied the recalling algorithm and undergo a systematic relaxation process. The results demonstrate that, if we increase the number of crucial points to be stored in CAM, a significant decrease in the number of correct pattern generated at the end of the simulations. However, the correct pattern is still within 85% to 100 % as the number of crucial points are being increased for every simulation. This implies that our proposed technique is efficient and consistent in retrieving the output after the training process.

Table 1. Global Pattern-SAT

Number of Crucial Points	The Global Pattern-SAT (%)
	Pattern-SAT (HNN-3SAT With McCulloch-Pitts Function)	Pattern-SAT (HNN-3SAT with Hyperbolic Tangent Activation Function)
5	99	100
10	99	100
15	96	100
20	95	100
25	92	99
30	90	99
35	87	96
40	85	95
45	82	95
50	82	90

Based on Table 1, Pattern-SAT with Hyperbolic Tangent activation function outperforms Pattern-SAT without any activation function in term of the number of correct pattern retrieved. When the number of neurons increased, Pattern-SAT with Hyperbolic Tangent activation is able to sustain more neurons. Thus, we can clearly observe from the result that the number of correct recalled pattern is consistently 100 until 20 crucial points and maintain 90 % of correctness when the 50 crucial points are used. The limit for our proposed model is until 50 neurons. After 50 neurons, the network is stuck in trial and error state in a long period of time. The whole patterns in exhaustive search method will be inactivated when one of the crucial points is not satisfied. In addition, it might take a longer time for the network to search the correct neuron states and proceed with the relaxation state, as the network spends more time in training state. However, the introduction of Hyperbolic Tangent activation function, which is well-known as a robust function by Sathasivam [28], will help the network to relax and be able to recall more patterns correctly. This method will give more time for the network to relax and retrieve the correct states systematically. On the contrary, less relaxation time will create spurious minima which will cause the retrieved solution to achieve local minima and produce wrong pattern. Hence, our proposed technique performs consistently in recalling the stored pattern in CAM under higher complexity and larger circumstances. Thus, the HNN-3SAT WITH Hyperbolic Tangent activation function outperformed McCulloch-Pitts function.

• B.    CPU Time

In this paper, the CPU time can be defined as the time taken for a logic program to generate and retrieve the correct patterns. Thus, it is an indicator to test the robustness of our proposed algorithm in pattern reconstruction involving 3-Satisfiability cases. Theoretically, our biological brain requires more time to store and retrieve any information if the complexity increases.

Table 2. CPU Time for the Pattern-SAT

Number of Crucial Points	CPU Time
	Pattern-SAT (HNN-3SAT without Activation Function)	Pattern-SAT (HNN-3SAT with Hyperbolic Tangent Activation Function)
5	5	2
10	19	8
15	230	56
20	783	122
25	1982	456
30	3400	723
35	6200	1169
40	13488	3204
45	25684	6422
50	66250	10450

Table 2 portrays the CPU time for the Pattern-SAT. According to the results obtained, it can be clearly seen that CPU time increases when the number of crucial points increases. For instance, the complexity of the network increased as the number of crucial points gets massive. We can see that the computational time increased when the number of neuron was getting higher. This is due to the condition when the network was getting larger and complex, the network was probably to get stuck in local minima and devour more computation time. As a result, extra time was needed to relax to global solution as the number of neurons increased. Moreover, the neurons needed to jump enormous energy barrier to reach the global solutions. On separate note, the pattern generation process whereby all the crucial points need to be activated usually consumes more computational time due to the trial and error process in hunting the satisfied interpretation.

The computation time obtained for Pattern-SAT with Hyperbolic Tangent activation function outperformed the McCulloch-Pitts in term of computation time. When we applied the Hyperbolic Tangent activation function to our network, the fixed bound allowed the network to retrieve the correct state much faster. Hence, the correct pattern can be obtained due to less computation burden for each number of crucial points. The traditional paradigm, McCulloch-Pitts function will retrieve the correct states in slower pace due to the complexity and computation burden.

• VII. C ONCLUSION

The direct implementation of logic programming in Hopfield network by implementing activation function in verifying the pattern satisfiability had been explored in this research. The number of correct pattern recalled and CPU time indicated that our proposed network, HNN-3SAT with Hyperbolic Tangent activation outperformed the HNN-3SAT with McCulloch-Pitts function in

Pattern-SAT. From the theory and experimental results, the proposed network with Hyperbolic Tangent activation function enhanced the chance of retrieving more correct patterns as the complexity is getting higher. The performance analysis is supported by the very good agreement of the global pattern and CPU time obtained.